Algoritma Pencarian Fuzzy TextRadar - Pendekatan Dasar

Algoritma Pencarian Fuzzy TextRadar - Pendekatan Dasar

Tidak seperti perbandingan string fuzzy, ketika kedua string yang dibandingkan adalah setara, string pencarian dan string data disorot dalam tugas pencarian fuzzy, dan perlu untuk menentukan bukan tingkat kesamaan dari dua string, tetapi tingkat keberadaan string pencarian dalam string data.

Pernyataan masalah

String data dan string pencarian diberikan sebagai set karakter sewenang-wenang yang terdiri dari kata - kelompok karakter yang dipisahkan oleh spasi.

Diperlukan untuk menemukan dalam baris data set fragmen yang paling dekat dengan baris pencarian oleh komposisi dan posisi relatif karakter.

Untuk menilai kualitas hasil pencarian, hitung koefisien relevansi, yang nilainya harus berkisar dari 0 hingga 1, di mana 0 harus sesuai dengan tidak adanya karakter string pencarian dalam string data, dan 1 harus sesuai dengan keberadaan string pencarian dalam string data dalam formulir tidak terdistorsi.

Pencarian harus dilakukan dengan analisis karakter-per-karakter dari baris sumber, dengan mempertimbangkan pengaturan timbal balik antara karakter dan kata-kata dalam baris, tetapi tanpa memperhitungkan sintaks dan morfologi bahasa.

Deskripsi algoritma

Pencarian dilakukan dalam beberapa tahap.

Konstruksi matriks kebetulan

Matriks kecocokan (M) adalah matriks dua dimensi, jumlah kolom yang sesuai dengan panjang string data, dan jumlah baris dengan panjang string pencarian. Elemen-elemen dari matriks kebetulan mengambil nilai 0 atau 1 tergantung pada apakah karakter yang sesuai dari garis bertepatan atau tidak, dengan pengecualian spasi (pembatas kata).
Matriks kecocokan untuk string data "ABCD EF" dan string pencarian "ABC" memiliki bentuk:



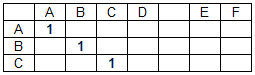
Elemen matriks pencocokan m (i, j) = 1 jika d (i) = s (j), di mana D adalah larik karakter string data, S adalah larik karakter string pencarian, i adalah nomor kolom dari matriks pencocokan M (nomor karakter dari string data ), j adalah nomor baris dari matriks kecocokan (jumlah karakter dalam string pencarian). Dalam kasus lain, m (i, j) = 0. Kecocokan pemisah kata (dalam kasus kami, spasi) tidak diperhitungkan, yaitu: m (i, j) = 0 jika d (i) = s (j) = '' .

Cocokkan Matrix Diagonals

Unsur-unsur dari matriks kebetulan M membentuk diagonal. Elemen matriks berada pada diagonal yang sama jika indeks i dan j secara bersamaan berbeda dengan +1 atau per - 1.



Diagonal sesuai dengan posisi string pencarian dalam urutan offset sepanjang string data.



Elemen dari salah satu diagonal dan perubahan yang sesuai pada gambar di atas disorot dengan warna biru.

Gagasan menggunakan urutan pergeseran garis relatif satu sama lain dalam masalah pencarian fuzzy kembali ke teknik terkenal untuk mendeteksi sinyal radar dengan latar belakang interferensi, yang melibatkan perhitungan fungsi korelasi timbal balik sinyal radio. Fungsi korelasi silang menentukan derajat kesamaan salinan dua sinyal berbeda v (t) dan u (t), digeser berdasarkan waktu τ relatif satu sama lain dan didefinisikan sebagai integral: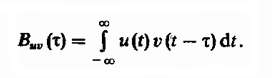



Jumlah total diagonal dihitung dengan rumus:



Panjang diagonal sama dengan panjang string pencarian.

Kelompok Pertandingan

Unit yang mengikuti secara berturut-turut dalam diagonal matriks kebetulan membentuk kelompok pertandingan. Di bawah ini adalah grup yang cocok untuk string data "ABCD DEF JH" dan string pencarian "ABC DE J" - 4 grup yang terletak di diagonal yang berbeda.

Matriks proyeksi

Diagonal matriks pertandingan dan grup pertandingan yang terkandung di dalamnya dipetakan ke bagian yang sesuai dari string pencarian dan string data, membentuk dua matriks proyeksi - string pencarian dan string data, masing-masing. Sebagai contoh kami, matriks proyeksi akan terlihat seperti ini:



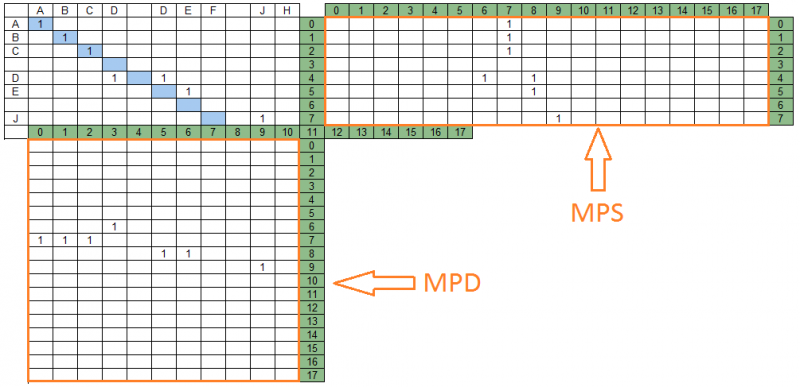
Pada gambar di atas, di sebelah kanan matriks kecocokan adalah matriks proyeksi ke string pencarian - MPS, di bawah - matriks proyeksi ke string data MPD. Jumlah kolom MPS sama dengan jumlah baris MPD dan sama dengan jumlah diagonal dari matriks pertandingan - dalam contoh kami, ada 18.

Cari sekelompok hasil

Untuk memecahkan masalah, perlu untuk menemukan seperangkat kelompok yang paling "menutupi" string pencarian, dengan fragmentasi paling kecil (sebesar mungkin), tanpa persimpangan satu sama lain dalam matriks proyeksi, dan pemetaan yang ke string data akan paling dekat dengan "asli" - string pencarian .

Persimpangan kelompok dalam matriks proyeksi

Dalam contoh kami, ada kelompok berpotongan dalam matriks MPS - pada gambar di bawah mereka disorot dengan warna merah. Selain itu, dalam matriks MPD, kelompok-kelompok yang sama ini tidak berpotongan, pada gambar mereka disorot dalam warna hijau.



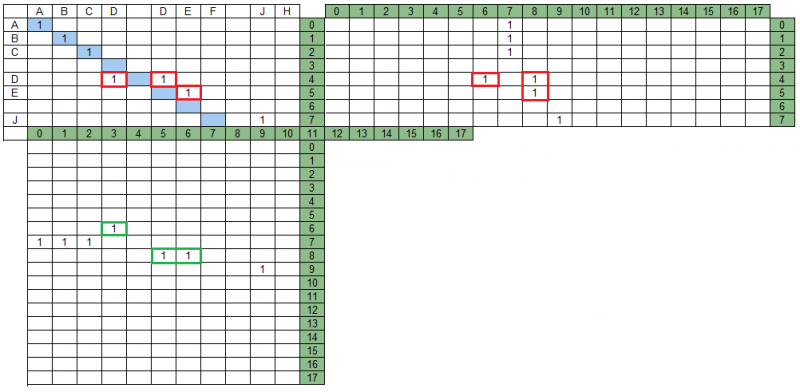
Pencarian untuk kumpulan kelompok yang dihasilkan menyiratkan bahwa tidak semua kelompok akan dimasukkan di dalamnya dan bahwa beberapa kelompok yang tersisa dapat dimodifikasi (terpotong) ketika menganalisis persimpangan timbal balik kelompok dalam proyeksi.

Pencarian untuk himpunan hasil dapat dilakukan dengan melalui siklus "tak terbatas" (jumlah iterasi dari siklus tidak melebihi jumlah kelompok) dari tabel semua kelompok , di mana kelompok matriks pertandingan awalnya ditempatkan, pada setiap iterasi di mana tindakan berikut akan dilakukan:

1. Memilih parameter terbaik berdasarkan parameter tertentu (tergantung pada konteks masalah yang sedang dipecahkan) - dalam kasus paling sederhana, ini mungkin merupakan pilihan kelompok pertama dengan ukuran terbesar yang muncul;
2. Penempatan grup terbaik di tabel grup hasil dan penghapusannya dari tabel semua grup (baris yang dirayapi);
3. Menghapus (atau memotong) dari tabel grup yang bersinggungan dengan grup terbaik yang dipilih dalam matriks proyeksi grup.

Rangkaian kelompok yang optimal untuk contoh kami disajikan pada gambar di bawah ini - kelompok yang disorot berwarna oranye.



Grup dihapus selama pemrosesan persimpangan (berpotongan dalam matriks MPS dengan kelompok terbaik dari iterasi kedua) disorot dalam warna merah.

Hasil pencarian di baris data akan terlihat seperti ini:

Perhitungan koefisien relevansi

Untuk menghitung hasil pencarian, panjang grup yang ditemukan dibandingkan dengan panjang kata dari string pencarian (penilaian komposisi grup), serta total panjang string pencarian dengan panjang grup yang ditemukan dalam string data. Diasumsikan bahwa signifikansi menilai komposisi kelompok yang ditemukan lebih tinggi daripada signifikansi estimasi tingkat dalam baris data, yang diperhitungkan dalam koefisien bobot rumus untuk menghitung koefisien relevansi:



Di mana koefisien komposisi grup dihitung sebagai rasio jumlah panjang kuadrat dari grup yang ditemukan dengan jumlah panjang kata-kata kuadrat dari string pencarian:



Faktor panjang adalah rasio panjang string pencarian dengan total panjang kelompok yang ditemukan pada string data. Jika nilai yang diperoleh dengan cara ini lebih besar dari 1, nilai kebalikannya diambil:



Sebagai contoh kita:

Perkiraan Cakupan Komputasi

Operasi yang paling intensif sumber daya adalah:

• penentuan matriks kecocokan M - jumlah elemen matriks didefinisikan sebagai produk dari panjang string pencarian dengan panjang string data: L * L;
• definisi matriks proyeksi pada data dan string pencarian - jumlah elemen matriks untuk MPS: (L + L - 1) * L, untuk MPD: (L + L - 1) * ;
• pembentukan tabel semua grup - jumlah grup tidak akan melebihi nilai L * L / 2;
• mencari kumpulan grup yang dihasilkan - jumlah iterasi siklus tidak melebihi jumlah awal grup, yaitu, L * L / 2.

Dengan demikian, jumlah total perhitungan akan menjadi kelipatan produk dari panjang string pencarian dengan panjang string data:



Linearitas jumlah perhitungan relatif terhadap ukuran sumber data merupakan argumen penting yang mendukung aplikasi praktis dari algoritma.

Nonlinier

Perlu dicatat bahwa linearitas disebabkan oleh prosedur yang disederhanakan untuk menemukan set kelompok yang dihasilkan. Dalam kasus umum, jika kami mempertimbangkan semua opsi yang memungkinkan untuk menempatkan grup pada baris data, dengan mempertimbangkan kemungkinan opsi pemrosesan persimpangan dan memilih set grup terbaik dari set kemungkinan, daripada memilih satu grup pada setiap iterasi siklus, maka jumlah perhitungan akan berhenti linier sehubungan dengan ukuran. sumber data. Ketergantungan nonlinear dari jumlah perhitungan pada ukuran data sumber sangat membatasi kemungkinan aplikasi praktis.

Temukan keseimbangannya

Untuk memastikan keseimbangan optimal antara kualitas pencarian dan kebutuhan akan sumber daya, penting untuk memilih metodologi pencarian yang benar untuk kumpulan kelompok yang dihasilkan, yang, sebagai suatu peraturan, dapat dilakukan dengan menggunakan fitur konteks dari masalah yang sedang dipecahkan.

Demo demo telah digunakan di situs web textradar.ru di mana Anda dapat menguji operasi algoritma.

Perbandingan dengan analog: Perbandingan algoritma pencarian fuzzy TextRadar dengan analog: Lucene, Sphinx, Yandex, 1C