Salah satu tugas paling sulit dalam sistem desain berbantuan komputer adalah mengisi ketika memodelkan objek dengan bentuk yang kompleks. Untuk konstruksi fillet, serta semua geometri dalam CAD, inti geometrik bertanggung jawab.

Dari sudut pandang pengembang kernel, tidak mungkin untuk mencakup semua opsi pembulatan karena keragamannya yang tak terbatas. Matematikawan kami terus menambahkan kasus khusus baru ke inti C3D, dan baru-baru ini melakukan pembulatan tiga wajah (atau pembulatan penuh).

Apa kompleksitasnya dan bagaimana algoritme bekerja, kata Anna Ladilova, matematikawan dan pemrogram di C3D Labs.

Apa pembulatan penuh?

Misalkan kita memiliki tubuh dengan tiga rantai wajah - tengah (atas) dan samping (kanan dan kiri). Hal ini diperlukan untuk mengganti permukaan tengah dengan permukaan fillet yang akan dengan lancar masuk ke permukaan samping yang berdekatan. Permukaan baru ini akan menjadi pembulatan penuh. Secara umum, ia memiliki radius variabel yang terdeteksi secara otomatis.



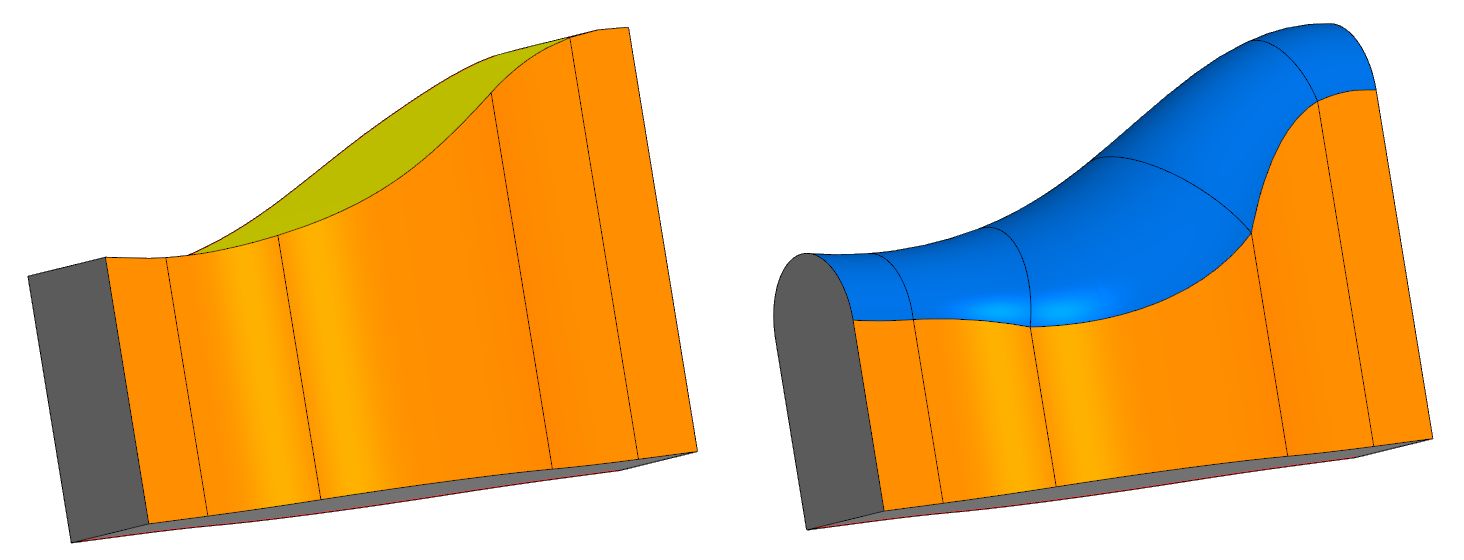
Dalam banyak sistem CAD yang terkenal, operasi fillet bulat dilaksanakan, tetapi matematikanya tidak diungkapkan.


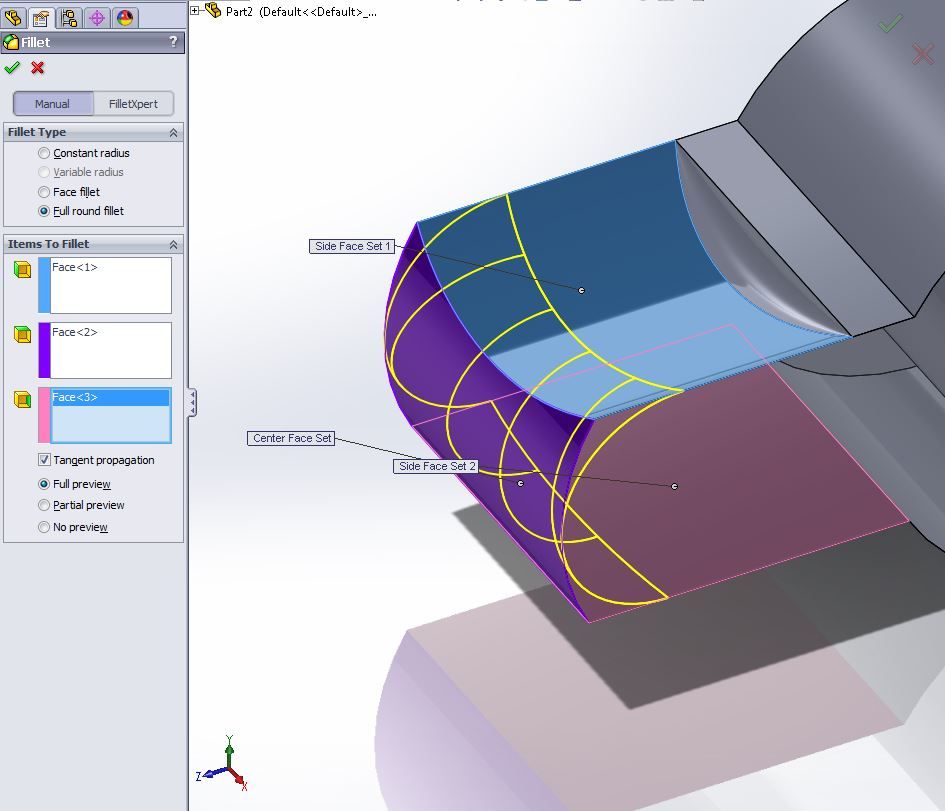Operasi fillet bulat penuh Solidworks

Karena itu, kami mengembangkan algoritme kami sendiri. Dan itu berbeda dari algoritma pengembang lain.

Operasi, meskipun disebut sama, menghasilkan hasil yang sedikit berbeda. Ini menunjukkan bahwa SolidWorks memberikan definisi yang berbeda untuk membulatkan tiga wajah.


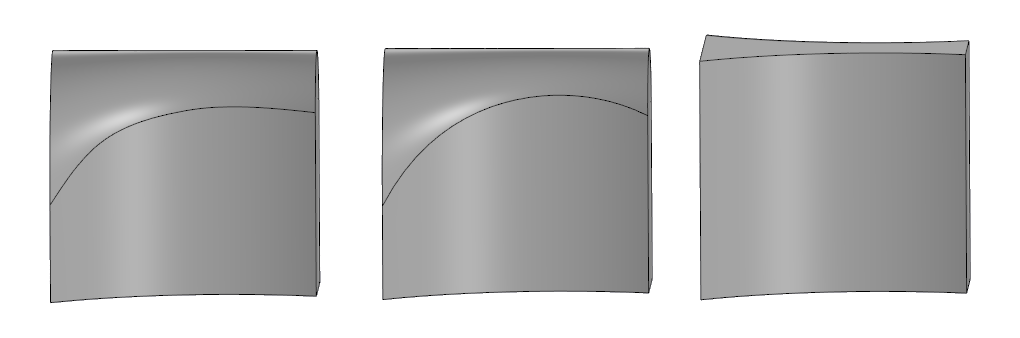Di sebelah kanan adalah model asli, di tengah adalah pembulatan penuh di SolidWorks, di sebelah kiri - di C3D.

Algoritma pembulatan penuh

Tugas membangun semua jenis fillet meliputi beberapa tahap:

1. Memecah rantai yang diberikan ke komponen dasar (untuk membulatkan tiga wajah itu persis tiga wajah: kiri, kanan dan tengah).
2. Secara konsisten mengatur komponen-komponen dasar.
3. Buat permukaan fillet untuk setiap komponen dasar.
4. Jahit permukaan fillet yang berdekatan dengan tulang rusuk.
5. Untuk memproses bagian akhir rantai fillet, mis., Sambungkan dengan benar ke badan yang dimodifikasi.

Titik kunci dalam prosedur ini adalah langkah ketiga: untuk membangun permukaan fillet untuk tiga wajah yang diberikan.

Untuk membangun permukaan yang diinginkan, pertama-tama perlu untuk menentukan kurva dimana fillet menyentuh masing-masing dari tiga wajah. Dalam kasus umum, kurva ini hanya dapat dibangun sebagai splines yang melewati titik-titik yang diketahui yang dihitung sebelumnya.

Pertimbangkan bagaimana Anda dapat menghitung tiga poin - satu di setiap spline.


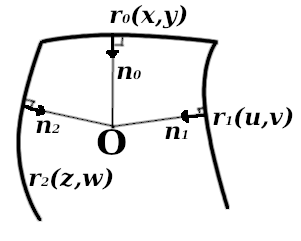
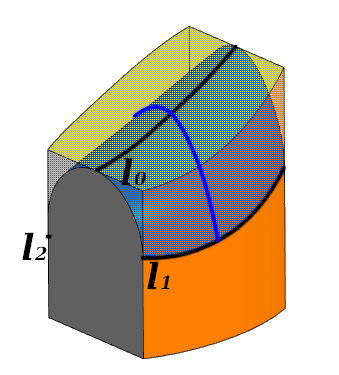Pemrosesan unsur. Fillet menyentuh masing-masing dari tiga wajah di sepanjang kurva l ₀ ; l ₁ ; l ₂ . Garis biru menunjukkan penampang

Di setiap bagian melintang $$$ABC$:

• $$$OA = OB = OC$- dihitung secara otomatis
• $$$OA, OB, OC$ortogonal ke bidang garis singgung permukaan pada titik yang sesuai
• $$$p$₀ - titik jangkar, terletak di pesawat $$$ABC$.

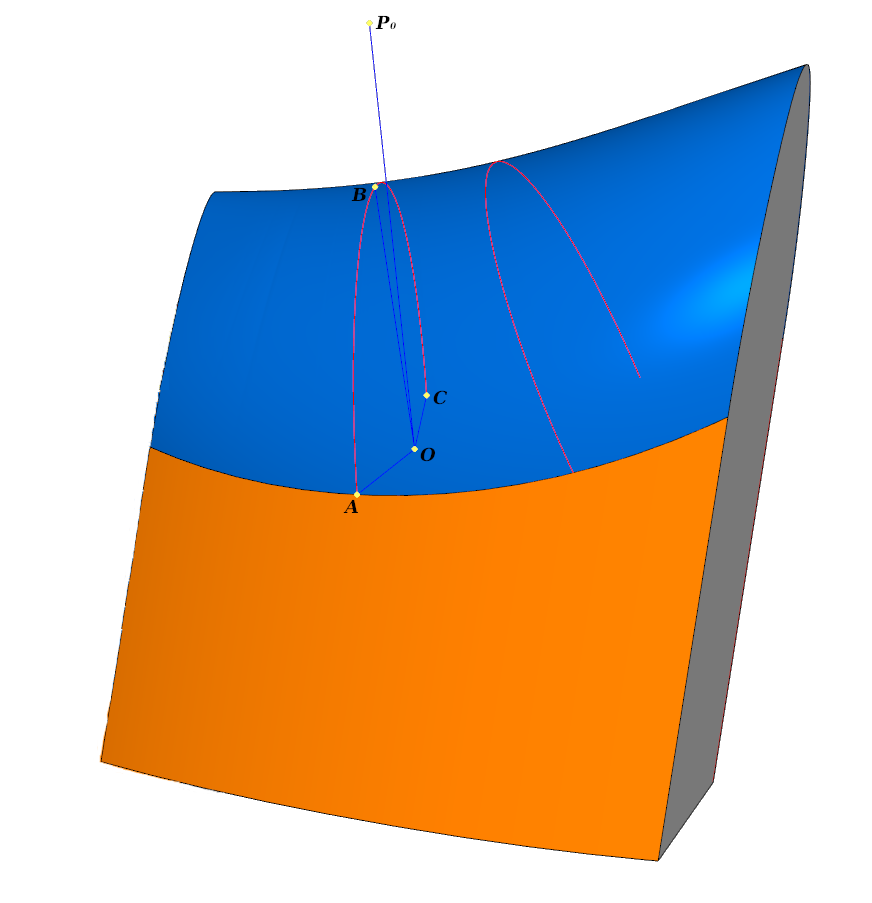
Kami mendefinisikan permukaan awal dari wajah tengah, kiri, dan kanan oleh vektor radius dalam domain definisi tertentu. Biarkan permukaan samping ditentukan oleh vektor radius $$$r$₁ $$$(u, v)$dan $$$r$₂ $$$(z, w)$dan yang sentral $$$r$₀ $$$(x, y)$. Kami memperkenalkan parameter numerik positif $$$d$.

Ditunjukkan oleh $$$n$₀ $$$(x, y)$, $$$n$₁ $$$(u, v)$, $$$n$₂ $$$(z, w)$satu normal ke permukaan yang sesuai, diarahkan "ke dalam".


Silangkan "bagian" saat membuat fillet

Kami meminta agar ujung-ujung normals ini masuk $$$d$kali, tekan satu titik - titik $$$O$.

Dalam hal geometri diferensial, persyaratan kami dapat dirumuskan dengan sistem tujuh persamaan dengan tujuh parameter:

$$$dn$₀ $$$(x, y)$= $$$dn$₁ $$$(u, v)$,
$$$dn$₀ $$$(x, y)$= $$$dn$₂ $$$(z, w)$,
( $$$r$₀ $$$(x, y)$- $$$p$₀ $$$r$₁ $$$(u, v)$- $$$p$₀ $$$r$₂ $$$(z, w)$- $$$p$₀ ) = $$$0$,

dimana

• $$$d$- radius variabel
• $$$p$₀ - titik jangkar
• $$$x, y, u, v, z, w$- variabel dari area definisi parameter.

Menggunakan algoritma metode numerik (misalnya, metode Newton), kami menemukan solusi untuk sistem ini: $$$x$₀ $$$y$₀ $$$u$₀ $$$v$₀ $$$z$₀ $$$w$₀ $$$d$₀ .

Solusinya mendefinisikan titik sentuh dengan permukaan:

• $$$r$₀ ( $$$x$₀ $$$y$₀ )
• $$$r$₁ ( $$$u$₀ $$$v$₀ )
• $$$r$₂ ( $$$z$₀ $$$w$₀ )

serta jari-jari $$$d$₀ .

Berlari melalui serangkaian poin $$$p$₀ , kami mendapatkan set tiga kali lipat titik singgung dengan permukaan tempat Anda dapat mengembalikan "kurva sentuh" $$$l$₀ $$$l$₁ $$$l$₂ ketika Hermite splines melewati poin yang dihitung.

Lingkup [ $$$t$_min $$$t$_maks ] semua kurva adalah sama, dan parameternya $$$t$_saya sesuai dengan suatu titik $$$r$_0i $$$r$_1i $$$r$_2i . Selanjutnya, kurva ini digunakan untuk menghitung penampang fillet yang diinginkan.

Kami memperbaiki beberapa parameter $$$t$dan hitung poin untuk itu:

• $$$r$₀ $$$(x (t), y (t)),$
• $$$r$₁ $$$(u (t), v (t)),$
• $$$r$₂ $$$(z (t), w (t))$.

Kami membangun kurva spline melewati titik-titik ini dan vektor normal ortogonal untuk mereka $$$n$₀ $$$(x (t), y (t))$, $$$n$₁ $$$(u (t), v (t))$, $$$n$₂ $$$(z (t), w (t))$sesuai.

Jika pernyataan masalah sedikit berubah dan kurva dicari pada titik yang diberikan dan vektor singgung pada titik-titik ini, maka metode dimana spline tersebut dapat diimplementasikan dapat ditemukan, misalnya, dalam buku Nikolai Golovanov "Geometric Modeling".

Buku ini menjelaskan secara rinci metode pembulatan tepi tubuh, khususnya, ditunjukkan bahwa penampang bundar dapat diwujudkan sebagai kurva NURBS yang ditentukan oleh tiga titik. Jika tiga wajah dibulatkan, kurva yang sama akan ditentukan oleh lima poin.

Jadi, untuk setiap parameter $$$t$kita dapat mendefinisikan satu set poin untuk membangun NURBS, dan oleh karena itu, tentukan setiap titik dari penampang permukaan fillet. Dengan demikian, masalah konstruksi permukaan sepenuhnya diselesaikan.

Ada pertanyaan kecil dalam uraian bagian algoritma ini - bagaimana memilih set poin “dengan benar” $$$p$₀ sesuai dengan penampang yang melaluinya akan mudah untuk mengembalikan "kurva sentuh" $$$l$₀ $$$l$₁ $$$l$₂ ?

Tampaknya masuk akal untuk membawa mereka dengan beberapa kurva yang dipilih sebelumnya. Kami tidak akan masuk ke rincian membangun kurva ini, kami hanya mencatat bahwa itu harus mulus, tanpa persimpangan diri dan "rata-rata" rantai tepi yang mengikat wajah tengah di kiri dan di kanan.


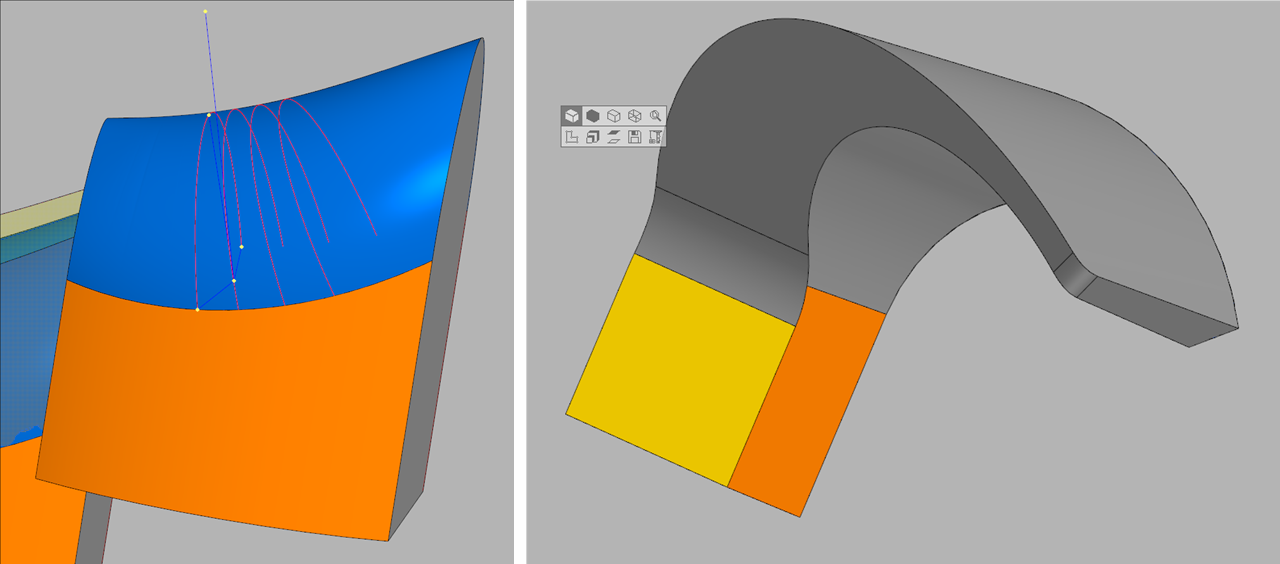Kiri, cross-sectional, tergantung titik $$$p$₀ .
Di sebelah kanan, angka bisa sangat kompleks, jadi memilih kurva "bantu" dengan benar adalah tugas yang terpisah.

Sekarang kita dapat membangun permukaan fillet untuk kasus dasar yang paling sederhana, kita dapat beralih ke masalah yang lebih kompleks: untuk membangun permukaan untuk rantai wajah.
Masalah utama di sini adalah untuk "menjahit" permukaan yang berdekatan dengan cara yang halus. Ini adalah langkah keempat dari algoritma.

Kesulitannya justru terletak pada kehalusan pengikatan silang, karena permukaannya dibangun dengan data awal yang berbeda. Untuk memastikan kelancaran, kita harus menggunakan berbagai trik: mengubah arah dan panjang vektor turunan dalam arah longitudinal pada jarak tertentu dari batas, mengubah nilai turunan dari fungsi bobot di batas, dll. Hasilnya terlihat pada gambar: garis zebra yang lebih halus sesuai dengan permukaan yang lebih halus.




Di atas adalah model tanpa algoritma perataan. Bawah - setelah menerapkan algoritma.

Ringkasan

Sebagai hasil dari penelitian kami, inti geometrik C3D mampu membangun penampang fillet, kurva pendukung, fillet dari tiga wajah; tahu cara menghaluskan permukaan dengan memilih parameterisasi; sebagian tahu bagaimana dengan lancar bergabung dengan permukaan fillet yang berdekatan.


Penulis - Anna Ladilova, Ph.D., matematikawan / programmer C3D Labs