Cara kerja kriptografi kurva elips di TLS 1.3

Beberapa peringatan pembaca:

Untuk (agak) menyederhanakan proses deskripsi dan memperketat volume artikel yang akan kita tulis, penting untuk membuat komentar yang signifikan dan segera menyatakan batasan utama - semua yang akan kami sampaikan kepada Anda hari ini tentang hal praktis sisi problematika hanya dapat dilakukan dalam hal TLS 1.3. Berarti bahwa sementara sertifikat ECDSA Anda masih akan bekerja di TLS 1.2 jika Anda menginginkannya, memberikan kompatibilitas ke belakang, deskripsi proses jabat tangan yang sebenarnya, pakaian sandi dan tolok ukur server klien hanya mencakup TLS 1.3 saja. Tentu saja, ini tidak berhubungan dengan deskripsi matematis dari algoritma di balik sistem enkripsi modern.

Artikel ini ditulis oleh matematikawan atau insinyur - meskipun mereka membantu menemukan jalan di sekitar matematika menakutkan dan meninjau artikel ini. Terima kasih banyak kepada karyawan Qrator Labs.

( E lliptic C urve) D iffie- H ellman ( E phemeral)

Warisan Diffie - Hellman di abad ke-21

Tentu saja, ini sudah dimulai dengan baik Diffie maupun Hellman. Tetapi untuk memberikan garis waktu yang benar, kita perlu menunjukkan tanggal dan acara utama.

Ada beberapa kepribadian utama dalam pengembangan kriptografi modern. Yang paling menonjol, Alan Turing dan Claud Shannon keduanya bekerja dalam jumlah yang luar biasa di bidang teori komputasi dan teori informasi serta kriptanalisis umum, dan baik Diffie maupun Hellman, secara resmi dikreditkan karena memunculkan gagasan kunci publik. (atau disebut asimetris) kriptografi (meskipun diketahui bahwa di Inggris ada kemajuan serius dalam kriptografi yang bertahan dalam kerahasiaan untuk waktu yang sangat lama), membuat kedua pria ini menjadi perintis.

Tepatnya apa?

Yah, ini mungkin terdengar aneh; Namun, sebelum 6 November 1976, tidak ada pengetahuan publik tentang sistem enkripsi kunci publik. Whitfield Diffie dan Martin Hellman (dan, pada kenyataannya, Ralph Merkle) - matematikawan, insinyur komputer dan penggemar, serta ahli kriptologi adalah yang pertama.

Bagi mereka yang tidak sadar - karena peran cryptanalysis mengambil alih selama Perang Dunia II dan dampaknya yang sangat besar pada menjaga informasi secara rahasia, kedua negara yang percaya bahwa mereka memiliki pengetahuan kriptografi paling maju - AS dan Inggris memasukkan enkripsi ke dalam Daftar Munisi mereka dan memanfaatkannya. larangan ekspor yang berat (secara bersamaan melemahkan implementasi enkripsi untuk penggunaan pribadi dan komersial dalam negeri). Untuk alasan ini, para peneliti Inggris yang bekerja di teknik pertukaran kunci asimetris di Kantor Pusat Komunikasi Pemerintah dan mengembangkan skema analog tidak diakui untuk penemuan ini sampai 1997, ketika pembatasan pada algoritma kriptografi dan deskripsi mereka dibuat tidak efektif.

Kembali ke penemu ganda kami - apa yang telah Diffie dan Hellman rubah secara khusus?

Mari kita lihat makalah asli mereka, dengan sempurna menggambarkan lompatan raksasa yang telah mereka perkenalkan (bahkan secara teoritis dengan makalah penelitian mereka):

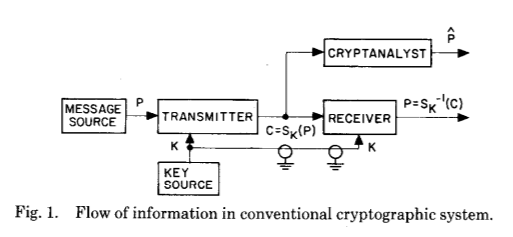
Dan yang berikut:

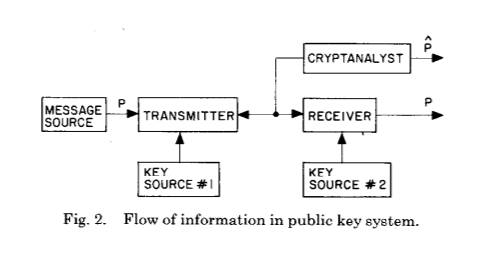
Kedua gambar ini dengan sempurna menggambarkan perubahan besar yang diperkenalkan Whitfield Diffie dan Martin Hellman setelah kriptografi dan kriptanalisis abad evolusi - pembentukan kunci rahasia bersama sebagai hasil dari perhitungan kriptografi.

Mari kita lihat gambar bagus lainnya dengan warna:



Ini menjelaskan apa yang sedang terjadi. Sebelum Diffie dan Hellman perjanjian kunci penemuan, hanya ada satu kunci simetris - digunakan baik untuk mengenkripsi dan mendekripsi pesan. Jika Anda ingin memberikan "kunci" kepada seseorang, itu harus ditransfer melalui saluran "aman". Anda dapat membayangkan semua batasan skema generasi sebelumnya - Anda membutuhkan saluran aman yang sudah ada, Anda tidak dapat menggunakan kembali kunci , dan, idealnya, panjang kunci harus sama dengan panjang pesan.

Claude Shannon dalam karyanya yang diklasifikasikan sebagai masa perang " Teori Komunikasi Sistem Kerahasiaan " membuktikan bahwa semua sandi yang tidak dapat dipecahkan secara teoritis harus memiliki persyaratan yang sama dengan pad satu kali - yang dikenal sebagai sandi Vernam, oleh penulis sandi aliran poliffabetik simetris ini.

Sekali lagi, kita akan melihat kertas aslinya:


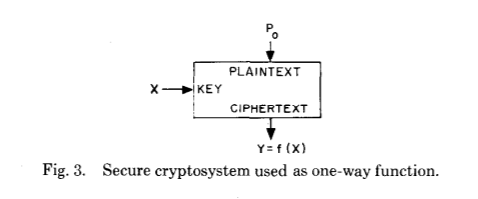
Sebelum kita melangkah lebih jauh, mari kita bertanya pada diri sendiri - bagaimana dua, bahkan jika brilian, manusia muncul dengan peningkatan yang begitu signifikan dalam bidang terapan dengan sejarah seperti itu, terutama pada saat perang?
Yah, karena:

• Teori informasi , dirumuskan oleh Claude Shannon;
• Teori perhitungan dipengaruhi oleh, terutama, Gereja Alonzo, John von Neumann, dan Alan Turing;
• Dan, yang lebih penting, teori komputabilitas sebagian besar didasarkan pada karya Turing, yang bisa kita katakan semua dikembangkan dan matang pada periode yang sama di abad ke-20. Diffie dan Hellman sama-sama menyebut Claude Shannon sebagai orang yang paling berpengaruh dalam pekerjaan mereka.

" Keamanan Universal " Lenstra menggambarkan jumlah energi yang dibutuhkan untuk "memecahkan" kriptografi simetris dengan berbagai panjang kunci. Ternyata memecahkan kunci kurva eliptik 228-bit yang panjang akan membutuhkan jumlah energi yang sama yang diperlukan untuk merebus semua air di Bumi. Namun, itu hanya valid dengan pertimbangan algoritma dan perangkat keras yang diketahui, karena, sebenarnya, tidak ada yang tahu apakah ada algoritma atau perangkat keras yang jauh lebih efisien. Kunci EC 228-bit sebanding dengan kunci RSA panjang 2380-bit, lebih lanjut tentang itu nanti. Meskipun dalam estimasi ini kunci RSA dan EC digunakan dalam skema enkripsi asimetris, panjang kunci semacam itu agak setara dengan kunci enkripsi simetris 128-bit.

Sangat mudah untuk membayangkan bahwa sesuatu yang "sulit untuk dihitung" akan membutuhkan banyak energi dan / atau waktu yang dibutuhkan untuk perhitungan. Kita cenderung berpikir bahwa komputer dapat "menghitung semuanya", tetapi ternyata itu tidak benar. Pertama, ada contoh-contoh yang tidak dapat dipastikan, seperti masalah penghentian, meskipun dalam bidang kriptografi, kita dapat menghindari perangkap ini. Kedua, jika kita mempertimbangkan waktu yang dibutuhkan untuk menjalankan algoritma tertentu, itu mungkin arbitrary tinggi. Itulah yang kami manfaatkan dalam kriptografi. Masalah dianggap "mudah" untuk dihitung jika waktu yang diperlukan untuk menjalankan masing-masing algoritma tergantung pada ukuran input (diukur dalam bit) seperti polinomial:$$ $ inline $ T (n) = O (n ^ k) $ inline $ , untuk beberapa konstanta positif$$ $ inline $ k $ inline $ . Dalam bidang teori kompleksitas komputasi , masalah tersebut membentuk kelas kompleksitas P.

Kelas kompleksitas P hampir menjadi pusat, karena mewakili masalah yang ada algoritma waktu polinomial deterministik. Kelas kompleksitas lainnya adalah NP (masalah yang “sulit” untuk dihitung), mewakili serangkaian masalah keputusan, yaitu, masalah yang membutuhkan jawaban “ya” atau “tidak”, yang memiliki bukti yang dapat diverifikasi dalam waktu polinomial. Anda melihat kata "bukti" di sini? Di situlah kita sampai ke fungsi pintu jebakan, milik kelas kompleksitas NP.


Kredit: xkcd

Fungsi satu arah; Fungsi trapdoor

Menurut definisi, fungsi satu arah adalah fungsi yang mudah untuk dihitung pada setiap input tetapi sulit untuk dibalik, yaitu menghitung input asli yang diberikan hanya output. "Mudah" dan "keras" merujuk pada definisi teori kompleksitas komputasi di atas. Menariknya, bahwa keberadaan fungsi satu arah tidak (secara matematis) terbukti karena keberadaan mereka akan membuktikan bahwa kelas kompleksitas P dan NP tidak sama, sedangkan P sama dengan NP atau tidak saat ini merupakan masalah terbuka. Jadi, perlu diingat bahwa semua kriptografi modern bergantung pada hipotesis yang tidak terbukti.

Sekarang, dalam makalah aslinya, Diffie dan Hellman memperkenalkan generasi lain dari fungsi satu arah yang mereka sebut "fungsi pintu jebakan". Bagaimana mereka berbeda?
Seperti yang mereka jelaskan dalam makalah tengara mereka:

Dalam kriptografi kunci-publik, penyandian dan penguraian diatur oleh kunci yang berbeda, E dan D, sehingga komputasi D dari E tidak dapat dilakukan secara komputasi (misalnya membutuhkan$$ $ inline $ 10 ^ {100} $ inline $ instruksi). Kunci penyandian E dapat diungkapkan [dalam direktori] tanpa mengurangi kunci penguraian D. Ini memungkinkan setiap pengguna sistem untuk mengirim pesan ke pengguna lain yang dienkripsi sedemikian rupa sehingga hanya penerima yang dimaksudkan yang dapat menguraikannya. .. Masalah otentikasi mungkin bahkan menjadi penghalang yang lebih serius terhadap adopsi universal telekomunikasi untuk transaksi bisnis daripada masalah distribusi utama ... [itu] ... adalah inti dari sistem apa pun yang melibatkan kontrak dan penagihan.

Dengan konvensi, karakter kriptografi "Alice" dan "Bob" (mencari komunikasi yang aman) sering digunakan untuk menjelaskan konsep kunci publik. Alice dan Bob menyetujui bilangan bulat besar$$ $ inline $ n $ inline $ dan$$ $ inline $ g $ inline $ dengan$$ $ inline $ 1 <g <n $ inline $ . Seleksi berdampak pada keamanan sistem. “Modulusnya$$ $ inline $ n $ inline $ harus menjadi yang utama; lebih penting$$ $ inline $ (n-1) / 2 $ inline $ juga harus menjadi yang utama <...> dan$$ $ inline $ g $ inline $ harus menjadi modulo root primitif$$ $ inline $ n $ inline $ <...> [dan]$$ $ inline $ n $ inline $ harus <...> paling tidak panjangnya 512 bit. ”Protokol Diffie - Hellman dapat dinyatakan dalam bentuk elemen dalam 5 langkah.

1. Alice memilih$$ $ inline $ x $ inline $ (bilangan bulat acak besar) dan menghitung$$ $ inline $ X = g ^ x \ bmod n $ inline $
2. Bob memilih$$ $ inline $ y $ inline $ (bilangan bulat acak besar) dan menghitung$$ $ inline $ Y = g ^ y \ bmod n $ inline $
3. Alice mengirim$$ $ inline $ X $ inline $ untuk Bob, sementara Bob mengirim$$ $ inline $ Y $ inline $ untuk Alice (mereka tetap$$ $ inline $ x $ inline $ dan$$ $ inline $ y $ inline $ rahasia satu sama lain)
4. Alice menghitung$$ $ inline $ k = Y ^ x \ bmod n $ inline $
5. Bob menghitung$$ $ inline $ k '= X ^ y \ bmod n $ inline $

Akibatnya Alice dan Bob memiliki nilai yang sama$$ $ inline $ k = k '$ inline $ yang berfungsi sebagai rahasia bersama.

Fungsi trapdoor adalah fungsi satu arah yang memungkinkan untuk menemukan kebalikannya jika seseorang memiliki informasi khusus yang disebut "pintu jebakan". Kedengarannya mudah, meskipun agak sulit untuk menemukan fungsi-fungsi tersebut - metode pertama yang layak ditemukan dalam implementasi algoritma enkripsi asimetris kriptografi kunci publik bernama RSA setelah penciptanya: Ron Rivest, Adi Shamir dan Leonard Adleman.

RSA

Dalam RSA kekerasan fungsi pembalikan didasarkan pada fakta bahwa anjak (mencari pengganda utama angka) membutuhkan waktu lebih banyak daripada perkalian, atau haruskah kita katakan di sini bahwa tidak ada metode waktu polinomial untuk memfaktorkan bilangan bulat besar pada komputer klasik memiliki telah ditemukan, bagaimanapun, belum terbukti bahwa tidak ada.

Di RSA, seperti dalam sistem enkripsi kunci publik lainnya, ada dua kunci: publik dan pribadi. RSA menerima pesan input (direpresentasikan sebagai string bit) dan menerapkan operasi matematika (modul eksponensial bilangan bulat besar) untuk mendapatkan hasil yang terlihat tidak dapat dibedakan dari acak. Dekripsi mengambil hasil ini dan menerapkan operasi serupa untuk mendapatkan kembali pesan aslinya. Dalam kriptografi asimetris, enkripsi dibuat dengan kunci publik dan dekripsi dengan yang pribadi.

Bagaimana? Karena operan milik grup siklik terbatas (satu set bilangan bulat dengan perkalian dalam aritmatika modular). omputer tidak berurusan dengan angka-angka besar yang sewenang-wenang, tetapi, untungnya, grup bilangan bulat kami adalah untuk melakukan operasi yang disebut "membungkus" - angka yang lebih besar dari jumlah maksimum yang diizinkan dibungkus ke angka dalam rentang valid yang kami operasikan . Ini memungkinkan kami untuk beroperasi dengan kunci yang panjangnya "tidak lebih dari". Dalam kurva eliptik, kriptografi, kelompok siklik (multiplikasi) digunakan juga tetapi dikonstruksi sedikit berbeda seperti yang akan kita lihat nanti.

Pada dasarnya yang dilakukan RSA adalah mengambil dua bilangan prima besar dan mengalikannya untuk mendapatkan apa yang disebut modulus. Semua angka lain yang harus ditangani berada di antara nol dan modulus. Modulus harus menjadi bagian dari kunci publik, dan panjang bitnya menentukan panjang kunci. Bagian kedua dari kunci publik adalah angka yang dipilih antara nol dan jumlah Euler (implementasi RSA modern mengambil jumlah Carmichael dan bukan Euler) dari modulus dengan beberapa batasan tambahan. Akhirnya, kunci pribadi harus dihitung dengan menyelesaikan beberapa persamaan modular. Untuk mengenkripsi angka, kami hanya menaikkannya ke kekuatan yang sama dengan kunci publik, dan untuk mendekripsi kembali nomor, kami menaikkannya ke kekuatan yang sama dengan kunci pribadi. Berkat sifat siklus grup, kami mendapatkan kembali angka awal.

Ada dua masalah signifikan dengan RSA saat ini, satu menjadi konsekuensi dari yang lain. Seiring panjang kunci (mis., Jumlah bitnya) tumbuh, faktor kompleksitas tumbuh tidak secepat yang diharapkan. Itu karena ada algoritma faktorisasi sub-eksponensial (tapi masih super polinomial ). Jadi, untuk menjaga tingkat keamanan yang tepat, panjang kunci RSA perlu tumbuh agak lebih cepat daripada panjang kunci ECC. Itu sebabnya kunci RSA yang paling luas saat ini adalah 2048 atau 3072 bit.

Beberapa saat kemudian, kita akan melihat dalam angka bagaimana panjang kunci mempengaruhi efisiensi cryptosystem secara keseluruhan dengan membandingkan sertifikat RSA dan ECDSA yang ditandatangani dengan otoritas Let's Encrypt.

( E lliptic C urve) D igital S ignature A lgorithm

Pencarian untuk fungsi pintu jebakan yang lebih baik akhirnya menyebabkan cryptographers untuk secara aktif berkembang di pertengahan 80-an cabang matematika yang didedikasikan untuk kurva elips.

Ini akan menjadi tugas utama untuk menggambarkan kriptografi kurva eliptik dalam satu artikel, jadi kita tidak akan melakukannya. Sebagai gantinya, mari kita lihat fungsi pintu jebakan kurva eliptik berdasarkan masalah logaritma diskrit.

Ada banyak primer dan pengantar yang lebih mendalam tentang kriptografi kurva eliptik, dan kami terutama akan merekomendasikan "ECC: pengantar lembut" karya Andrea Corbellini jika Anda tertarik pada matematika.

Yang kami minati adalah parameter yang “sederhana”.

Kurva eliptik didefinisikan oleh persamaan seperti ini:$$ $ inline $ y ^ 2 = x ^ 3 + ax + b $ inline $
Kurva seperti itu diperlukan untuk membangun subkelompok siklik di atas bidang yang terbatas. Oleh karena itu, parameter berikut digunakan:

• Perdana$$ $ inline $ p $ inline $ yang menentukan ukuran bidang hingga;
• Koefisien$$ $ inline $ a $ inline $ dan$$ $ inline $ b $ inline $ persamaan kurva eliptik;
• Titik dasar$$ $ inline $ g $ inline $ yang menghasilkan subkelompok yang disebutkan;
• Pesanan$$ $ inline $ n $ inline $ dari subkelompok;
• Kofaktor$$ $ inline $ h $ inline $ dari subkelompok.

Kesimpulannya, parameter domain untuk algoritma kami adalah sextuplet$$ $ inline $ (p, a, b, G, n, h) $ inline $ .
Kurva eliptik seperti itu bekerja di atas bidang hingga$$ $ inline $ \ mathbb {F} _p $ inline $ dimana$$ $ inline $ p $ inline $ adalah bilangan prima yang agak besar. Jadi kami memiliki satu set bilangan bulat modulo$$ $ inline $ p $ inline $ , di mana operasi, seperti penjumlahan, pengurangan, perkalian, inversi aditif, inversi multiplikatif dimungkinkan. Penambahan dan perkalian bekerja mirip dengan aritmatika "jam" modular atau biasa kita lihat di RSA "wrap arounds".
Karena kurva simetris tentang sumbu x, diberikan titik apa pun$$ $ inline $ P $ inline $ , kita bisa ambil$$ $ inline $ −P $ inline $ menjadi titik sebaliknya. Kami ambil$$ $ inline $ −O $ inline $ menjadi adil$$ $ inline $ O $ inline $ .
Penambahan untuk titik kurva didefinisikan dengan cara yang memberikan poin$$ $ inline $ P $ inline $ dan$$ $ inline $ Q $ inline $ , kita bisa menggambar garis yang memotong kedua titik tersebut dan kurva yang memotong di titik ketiga$$ $ inline $ R $ inline $ jadi itu$$ $ inline $ P + Q = -R $ inline $ dan$$ $ inline $ P + Q + R = 0 $ inline $ .

Mari kita lihat penjelasan Marc Hughes :

Garis kemiringan konstan yang bergerak di sepanjang permukaan torus ditunjukkan di atas. Baris ini melewati dua titik integer yang dipilih secara acak pada kurva.



Untuk menambahkan dua titik pada grafik, gambarlah garis dari titik yang dipilih pertama$$ $ inline $ P $ inline $ ke titik yang dipilih kedua$$ $ inline $ Q $ inline $ , dan perluas garis sampai memotong titik lain pada grafik$$ $ inline $ -R $ inline $ , perluas melintasi batas plot jika perlu.

Setelah Anda mencegat titik integer, mencerminkan titik secara vertikal di tengah grafik (garis oranye bertitik) untuk menemukan titik baru$$ $ inline $ R $ inline $ pada grafik. Oleh karena itu$$ $ inline $ P + Q = R $ inline $ .

Perkalian dengan skalar sekarang sepele:$$ $ inline $ n \ cdot P = P + P + P + \ dots + P $ inline $ (ini dia$$ $ inline $ n $ inline $ summands).

Fungsi pintu jebakan di sini terletak di dalam masalah logaritma diskrit (untuk kurva elips), bukan faktorisasi yang kami lihat di dalam bagian RSA. Masalahnya adalah: jika kita tahu$$ $ inline $ P $ inline $ dan$$ $ inline $ Q $ inline $ , apa itu$$ $ inline $ k $ inline $ itu$$ $ inline $ Q = k \ cdot P $ inline $ ?

Baik masalah faktorisasi (yang mendasari RSA) dan logaritma diskrit untuk kurva elips (yang merupakan dasar untuk ECDSA dan ECDH) seharusnya sulit, mis., Tidak ada algoritma yang diketahui untuk memecahkan masalah ini dalam waktu polinomial untuk kunci yang diberikan panjangnya

Sementara, biasanya, siapa pun akan dipermalukan karena mencampurkan pertukaran kunci (ECDH) dengan algoritma tanda tangan (ECDSA), kita perlu menjelaskan bagaimana mereka bekerja bersama. Sertifikat TLS modern berisi kunci publik, dalam kasus kami, dari pasangan kunci yang dihasilkan algoritma kurva eliptik, biasanya ditandatangani oleh otoritas tingkat yang lebih tinggi. Klien memverifikasi tanda tangan server dan mendapatkan rahasia bersama. Rahasia bersama digunakan dalam algoritma enkripsi simetris, seperti AES atau ChaCha20. Namun, prinsipnya tetap sama: sepakati parameter domain (sextuplet), dapatkan pasangan kunci, di mana kunci pribadi adalah bilangan bulat yang dipilih secara acak (multiplicand dari$$ $ inline $ Q = k \ cdot P $ inline $ ), dan kunci publik adalah titik di kurva. Algoritme tanda tangan menggunakan titik dasar$$ $ inline $ g $ inline $ , yang merupakan generator untuk subkelompok pesanan utama yang besar$$ $ inline $ n $ inline $ , seperti itu$$ $ inline $ n \ cdot G = 0 $ inline $ , di mana 0 adalah elemen identitas. Tanda tangan membuktikan bahwa koneksi aman sedang dibuat dengan pihak asli - server yang memiliki sertifikat TLS (kunci publik) yang ditandatangani oleh beberapa otoritas sertifikat untuk nama server yang diberikan.

(EC) DH (E) + ECDSA = Bentuk jabat tangan saat ini

Dalam TLS modern (1.3) klien dan server menghasilkan pasangan kunci publik-pribadi mereka dengan cepat, sementara membuat koneksi, ini disebut versi kunci pertukaran Ephemeral. Perpustakaan TLS browser paling populer mendukung ini. Sebagian besar mereka menggunakan kurva eliptik Edwards 25519 , diperkenalkan oleh Daniel J. Bernstein (djb), menawarkan keamanan 128-bit. Sejak 2014 openssh menggunakan kurva ini untuk pembuatan pasangan kunci. Pada tahun 2019, browser masih tidak mendukung sesi TLS dengan server yang memiliki sertifikat dengan kunci publik EdDSA.

Tapi mari kita kembali ke bagaimana semuanya bekerja pada akhir 2019 dengan TLS 1.3.

Mekanisme pertukaran kunci dalam TLS 1.3 terbatas pada (EC) DH (E) berbasis (dengan x25519 adalah yang didukung di perpustakaan TLS sisi klien dari browser paling populer serta perpustakaan TLS sisi server, seperti OpenSSL, yang akan kami periksa sedikit kemudian), dan daftar paket sandi hanya berisi tiga entri: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 dan TLS_CHACHA20_POLY1305_SHA256. Bagi Anda yang mengetahui bagaimana cipher suites diberi nama dalam versi TLS 1.2, segera terlihat bahwa mekanisme pertukaran kunci sekarang "terlepas" dari nama cipher suite, juga RSA statis dan Diffie - Hellman yang statis, mode pertukaran dihapus. dari spesifikasi seluruhnya. Bahkan dimulainya kembali sesi berdasarkan PSK dibuat lebih dari ECDHE di TLS 1.3. Hal ini juga berlaku untuk parameter DH khusus, yang tidak diizinkan sekarang, hanya menyisakan yang umumnya disepakati untuk aman dalam spesifikasi protokol final.

Sangat menarik bahwa ada perbedaan yang cukup signifikan dalam cara kerja algoritma enkripsi asimetris saat ini. Dengan ECC (dan sertifikat ECDSA pada khususnya) kami menggunakan kunci yang lebih kecil untuk mencapai tingkat keamanan yang "nyaman", dibandingkan dengan RSA. Itu memungkinkan penggunaan algoritma enkripsi asimetris yang lebih kuat dan mekanisme pertukaran kunci pada perangkat yang lebih kecil dan kadang-kadang bahkan dalam hal-hal yang umumnya tidak dianggap sebagai perangkat (smartcard).

Pertama-tama, perlu disebutkan apa yang dimaksud dengan "cryptosystem hybrid" dalam hal TLS 1.3.
Hybrid cryptosystem adalah yang menggunakan enkripsi asimetris (kunci publik) untuk membangun rahasia bersama, yang selanjutnya digunakan sebagai kunci dalam aliran simetris atau blok cipher.

Kedua, infrastruktur dan sertifikat kunci publik. Sangat menarik bahwa dalam wawancara 2004 Martin Hellman menyebutkan "pahlawan tanpa tanda jasa" Loren Kohnfelder, yang tesis sarjana MIT-nya memperkenalkan struktur pohon dari apa yang sekarang kita kenal sebagai infrastruktur kunci publik. Namun demikian, mari kembali ke sertifikat.

Fakta bahwa server benar-benar memiliki kunci pribadi dijamin oleh tanda tangannya, yang dapat diverifikasi dengan kunci publik server. Dan sertifikat memastikan bahwa beberapa kunci publik milik server tertentu. Ini berarti bahwa Anda menjalin komunikasi yang aman dengan pihak tertentu dan bukan dengan penipu. Bank Anda, bukan penjahat cyber. Dalam TLS 1.3 terdapat peningkatan yang signifikan dibandingkan format negosiasi sebelumnya - server menandatangani semua informasi yang dimilikinya hingga saat ini: klien menyapa dan server menyapa, termasuk cipher yang dinegosiasikan. Mari kita lihat bagian yang sesuai dari RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

Dalam TLS 1.3 klien mengirim pembagian kunci (bersama dengan parameter yang diperlukan), algoritma tanda tangan segera di pesan pertama (Klien Halo). Kunci yang diperlukan untuk bertukar dengan server dibuat di latar belakang, tanpa pengguna bahkan menyadari fakta itu. Mereka selanjutnya ditukar dengan server untuk membuat rahasia umum, dari kunci-kunci rahasia pra-master yang dibuat ketika server mengirim pesannya (Server Hello) menjawab klien.
Di sisi "Server Halo" Anda dapat melihat Sertifikat * ditransfer ke klien, bersama dengan bagian Verifikasi Sertifikat * yang memverifikasi bahwa pihak tersebut memiliki kunci pribadi untuk entri kunci publik yang sesuai, dan membuat kunci sesi (simetris) jika semuanya berjalan sesuai rencana - artinya, pihak yang meminta data (klien) berhasil memverifikasi pihak penjawab (server), yang selanjutnya menciptakan rahasia umum.

Ada dua operasi penting yang disembunyikan dalam transmisi ini - pembuatan tanda tangan dan verifikasi tanda tangan. Itu dibuat di kedua sisi komunikasi karena "tanda tangan" pada dasarnya adalah bukti bahwa pihak tersebut sebenarnya memiliki kunci pribadi yang sesuai dengan kunci publik, bahwa data berasal dari penandatangan dan pesan tidak diubah dalam perjalanan.

Dengan RSA, seperti yang akan kita lihat lebih lanjut, operasi penandatanganan adalah yang paling mahal. Karena kami menandatangani dengan kunci panjang 2048 atau 3072-bit, operasi seperti itu memuat server secara signifikan, lebih banyak daripada memuat klien yang memverifikasi tanda tangan tersebut.

Dengan ECDSA, kami memiliki kunci yang lebih kecil (kami akan melihat ECDSA dengan NIST P-256 (atau secp256v1)) tetapi operasi yang lebih kompleks. Akibatnya, itu dapat dilihat sebagai RSA "terbalik" - klien dimuat paling banyak, dengan perhitungan verifikasi tanda tangan, sementara server dengan mudah menangani pembuatan tanda tangan. Pengukuran memverifikasi bahwa, lihat bagian "Sedikit patokan".

Efek ini dengan mudah skala Internet saat ini - karena klien modern hampir sama kuatnya dengan server (mengingat hanya frekuensi inti CPU), sehingga mereka dapat secara efektif mengambil operasi mahal untuk telanjang. Server, pada gilirannya, dapat menggunakan kemampuan yang dibebaskan untuk membuat lebih banyak tanda tangan dan membuat lebih banyak sesi.

Mari Enkripsi tanda tangan sertifikat

Jadi, untuk memberikan pembaca sedikit petunjuk praktis dan praktis tentang cara membuat server yang mendukung TLS dengan pasangan kunci ECDSA yang ditandatangani oleh otoritas Let's Encrypt, kami memutuskan untuk mengilustrasikan proses penuh untuk menciptakan pasangan kunci yang diperlukan. untuk membuat CSR (permintaan penandatanganan sertifikat) untuk Let's Encrypt dan, sebagai hasilnya, dapatkan sertifikat ECDSA yang diperlukan untuk server kami.

Kami harus membuat kunci pribadi untuk melanjutkan. Kami akan menggunakan pustaka OpenSSL.
Manual OpenSSL menjelaskan pembuatan kunci EC apa pun melalui perintah khusus, yang dirancang khusus untuk cabang kurva eliptik dari algoritma pembuatan.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

Untuk memeriksa apakah pustaka OpenSSL melakukan semuanya dengan benar, kita dapat menjalankan perintah ec .

 openssl ec -in privatekey.pem -noout -text 

Output akan menunjukkan kepada kita kurva yang ditentukan dengan kunci yang telah dibuat.

Langkah selanjutnya sangat penting untuk penciptaan CSR - untuk melewati proses mengisi semua rincian informasi yang diperlukan untuk mendapatkan sertifikat kita memerlukan file konfigurasi. Untungnya, Mozilla melakukan seluruh pekerjaan untuk kami, memperkenalkan " Generator Konfigurasi SSL ". Di sana, Anda dapat memilih dari opsi server yang tersedia. Konfigurasi OpenSSL murni, secara khusus tidak ada pada halaman Generator akan terlihat seperti ini:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

Catatan: Anda tidak perlu memiliki CNF - jika tidak, Anda akan diminta untuk mengisi perincian ini di baris perintah.

Sekarang, ikuti pembuatan CSR itu sendiri. Di sini kita memiliki perintah OpenSSL yang berguna.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

Kami juga dapat memverifikasi kebenaran CSR yang baru dibuat.

 openssl req -in csr.pem -noout -text -verify 

Di sini kita telah sampai pada tahap akhir - menggunakan klien ACME, certbot, untuk meneruskan permintaan penandatanganan sertifikat kami ke Let's Encrypt.

Certbot membantu Anda mendapatkan sertifikat yang diperlukan dan memiliki banyak opsi. Di sini dikatakan, jika Anda baru mengenal enkripsi kunci publik, dan infrastruktur PKI yang kami miliki pada tahun 2019, Anda sebaiknya menggunakan --dry-run sebelum Anda mencoba mendapatkan sertifikat untuk domain apa pun dari domain Anda.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

Dalam kasus ini, klien certbot memeriksa apakah daftar domain yang diminta (pada baris perintah) cocok dengan domain yang tercantum dalam permintaan penandatanganan sertifikat. Dalam perintah --dns-somednsprovider terletak sedikit kebohongan, karena ada banyak cara yang bisa Anda buktikan. Mari Enkripsi Anda memiliki bagian tertentu dari lalu lintas Internet. Namun, jika Anda menggunakan penyedia hosting awan publik, katakan DigitalOcean, Hetzner, Amazon, Azure, apa pun - mungkin akan ada cara yang lebih alami untuk memberikan informasi yang diperlukan, karena penyedia Anda sudah membuat beberapa alat integrasi.

Setelah, jika Anda yakin tentang kebenaran dari parameter yang Anda gunakan dalam meneruskan CSR Anda ke Let's Encrypt melalui klien certbot - kecualikan --dry-run dari perintah Anda dan lanjutkan.

Jika berhasil, klien akan menghasilkan beberapa sertifikat sebagai output: sertifikat yang ditandatangani itu sendiri, sertifikat root dan perantara, dan kombinasi yang terakhir sebagai rantai sertifikat yang terakhir disebut, semua dalam format file .pem.

OpenSSL memiliki perintah yang dapat kita gunakan untuk memeriksa sertifikat:

 openssl x509 -in chainfilepath.pem -noout -text 

Pada titik ini, menjadi jelas bahwa Let's Encrypt menandatangani sertifikat menggunakan SHA256 digest. Selain itu, penandatanganan Root dan Intermediate ECDSA berada di bawah bagian "Fitur Mendatang", yang secara efektif berarti bahwa saat ini Anda hanya akan mendapatkan perantara RSA. Tapi tidak apa-apa karena Anda masih menggunakan kunci publik ECDSA.

Di akhir bagian ini, kami ingin mengatakan sesuatu sehubungan dengan panjang kunci. Dalam keamanan informasi, adalah umum untuk mengatakan tingkat keamanan adalah 2 ^ x, di mana x adalah panjang bit (RSA adalah sedikit pengecualian di sini, karena ia tumbuh agak lebih lambat daripada secara eksponensial). Untuk memperkirakan bagaimana kunci yang digunakan untuk algoritma yang berbeda saling bersesuaian, kami akan merujuk ke halaman wiki OpenSSL.
Seperti yang Anda lihat, perbedaannya cukup menonjol. Meskipun dengan Let's Encrypt kami tidak bisa mendapatkan sertifikat yang ditandatangani di luar 256 (secp256v1) dan 384 (secp384r1) kunci kurva eliptik.

Masalah dan pengecualian yang diketahui, dan THE NSA

Kredit: xkcd

Mungkin, masalah utama menggunakan kriptografi kurva eliptik selama bertahun-tahun adalah perlunya generator angka acak yang dibuat dengan sangat hati-hati, untuk membuat kunci tingkat keamanan yang diperlukan.

Ada skandal besar di sekitar algoritma Dual_EC_DRBG (dual elliptic curve deterministic random bit), yang membutuhkan waktu bertahun-tahun untuk menyelesaikannya. Juga, ada ketidakpastian di sekitar paten ECC, seperti diketahui bahwa banyak dari mereka milik perusahaan Certicom, yang diakuisisi oleh Blackberry. Ada juga perusahaan yang diketahui bersertifikat penggunaan ECC dari Blackberry. Tentu saja, ada ketidakpercayaan sederhana pada beberapa standar NIST, yang dapat atau tidak dapat dipengaruhi oleh NSA atau institusi penegakan dan pengawasan Amerika Serikat lainnya.

Sisi implementasi dari suatu masalah adalah pertanyaan yang sama sekali berbeda. Pada tahun 2010 konsol PlayStation 3 mengalami pemulihan kunci privat Sony karena implementasi yang tidak tepat dari algoritma ECDSA - mereka memiliki acak statis yang membuat fungsi pintu jebakan dipecahkan. OpenSSL juga menderita pada tahun berikutnya, namun, dengan cepat memperbaiki kerentanan yang memungkinkan pengambilan kunci privat dengan bantuan serangan waktu, untuk informasi lebih lanjut lihat kertas asli .

Pada 2013 di konferensi RSA, sekelompok peneliti mempresentasikan “ Gagal Secara Acak! ”Makalah tentang kerentanan kelas Java SecureRandom. Setengah tahun kemudian datang ke dompet Bitcoin Android , dibuat dengan menggunakan PRNG yang tidak cukup aman secara kriptografis.

Karena kerentanan serial yang serius ditemukan, pada bulan Agustus 2013 yang sama, IETF merilis RFC 6979 , menggambarkan generasi deterministik k yang digunakan dalam pembuatan kunci. Kita dapat mengatakan bahwa tindakan semacam itu memperbaiki masalah, tetapi kita tidak akan melakukannya - kapan saja para peneliti dapat menemukan masalah dalam berbagai implementasi karena penyimpangan yang tidak perlu dari spesifikasi protokol.

Tentang NSA. Jika Anda belum pernah mendengar tentang cerita Dual_EC_DRBG - meluangkan waktu dan membaca artikel yang sesuai, Anda tidak akan menyesal masuk ke detail. Edward Snowden adalah bagian dari kisah ini karena wahyu 2013 membuktikan kecurigaan sebelumnya. Itu mengakibatkan banyak cryptographers terkemuka kehilangan kepercayaan kepada NIST karena organisasi itu merancang dan mendeskripsikan banyak kurva dan algoritma lebih lanjut, yang mendasari ECDSA.

Fungsi 25519 kurva dan fungsi Daniel Bernstein adalah jawaban untuk kedua masalah ini dan, seperti yang kami jelaskan sebelumnya, transisi menuju EdDSA lambat meskipun terbukti. Bahkan dengan kurva NIST, tidak ada bukti kerentanan mereka telah ditemukan dan, seperti yang telah kami sebutkan, pengalaman yang terkait secara acak telah cukup instruktif.

Untuk mengakhiri bagian ini, kami ingin memberikan kutipan John von Neumann: "Siapa pun yang berusaha menghasilkan angka acak dengan cara deterministik, tentu saja, hidup dalam keadaan berdosa."

Sedikit patokan

Kami menggunakan server NGINX 1.16.0 dengan OpenSSL 1.1.1d untuk menjalankan benchmark ini dengan berbagai sertifikat. Seperti yang kami sebutkan sebelumnya, saat ini Mari Enkripsi hanya memungkinkan algoritma prime256v1 dan secp384r1 untuk permintaan penandatanganan sertifikat, dan tidak menyediakan sertifikat ECDSA root dan perantara, mungkin bekerja pada fitur ini pada saat kami menulis artikel ini.
Seperti yang Anda lihat, untuk satu inti CPU Intel® Xeon® Silver 4114 @ 2.20GHz (diluncurkan Q3'17), perbedaan keseluruhan dalam kinerja ECDSA, dibandingkan dengan RSA 2048 yang diadopsi secara luas adalah 3,5x.

Sekarang mari kita lihat hasil kecepatan-OpenSSL prosesor yang sama dengan ECDSA dan RSA.
Di sini kita dapat melihat konfirmasi untuk tesis yang diberikan sebelumnya tentang biaya komputasi yang berbeda untuk menandatangani dan memverifikasi operasi ECC dan RSA. Akibatnya, saat ini dilengkapi dengan TLS 1.3 ECC memberikan peningkatan kinerja yang signifikan pada tingkat keamanan bit yang lebih tinggi, dibandingkan dengan RSA. Itulah alasan paling mendasar mengapa kami di Qrator Labs mendorong klien kami untuk mengadopsi ECDSA. Dengan CPU modern, Anda mendapatkan hampir perbedaan 5x dalam mendukung ECDSA.

Jika Anda tertarik pada bagaimana CPU Anda melakukan perhitungan kriptografi, Anda dapat menjalankan perintah openssl speed sederhana. -rsa , -ecdsa dan -eddsa akan memberi Anda hasil benchmark untuk algoritme tanda tangan yang sesuai.

(Superposisi) Masa Depan

Kredit: djb

Sangat ironis bahwa ketika kami sedang mempersiapkan artikel ini, Google mengumumkan " mencapai supremasi kuantum ". Apakah ini berarti bahwa kita dalam bahaya sekarang dan segala sesuatu yang berkembang hingga saat ini tidak memberikan kerahasiaan?

Ya tidak.

Seperti yang ditulis Bruce Schneier dalam esainya untuk Keamanan dan Privasi IEEE “ Kriptografi setelah Tanah Alien ”, sebuah pukulan besar dengan komputer kuantum yang cukup kuat dapat dilakukan terhadap kriptografi kunci publik (asimetris). Kriptografi simetris masih akan kuat.

Kami ingin mengutip Bruce Schneier sebagai berikut:

Ada satu lagi skenario masa depan yang perlu dipertimbangkan, satu yang tidak memerlukan komputer kuantum. Sementara ada beberapa teori matematika yang mendukung satu arah yang kita gunakan dalam kriptografi, membuktikan validitas teori-teori itu sebenarnya adalah salah satu masalah besar yang terbuka dalam ilmu komputer. Seperti halnya kriptografer pintar untuk menemukan trik baru yang membuatnya lebih mudah untuk memecahkan algoritma tertentu, kita dapat membayangkan alien dengan teori matematika yang cukup untuk memecahkan semua algoritma enkripsi. Bagi kami, hari ini, ini konyol. Kriptografi kunci publik adalah semua teori bilangan, dan berpotensi rentan terhadap alien yang cenderung matematis. Kriptografi simetris adalah begitu banyak kekusutan nonlinear, begitu mudah untuk membuat lebih kompleks, dan begitu mudah untuk menambah panjang kunci, bahwa masa depan ini tidak terbayangkan. Pertimbangkan varian AES dengan ukuran blok dan kunci 512-bit, dan 128 putaran. Kecuali matematika secara fundamental berbeda dari pemahaman kita saat ini, itu akan aman sampai komputer terbuat dari sesuatu selain materi dan menempati sesuatu selain ruang.

Tetapi jika hal yang tak terbayangkan terjadi, itu akan meninggalkan kita dengan kriptografi hanya berdasarkan teori informasi: pembalut satu kali dan variannya.

Ini adalah area di mana, kecuali mencari kekurangan implementasi, sebagian besar masalah dapat ditemukan. Jika ada sekelompok ahli matematika, cryptanalysts / cryptographers, dan insinyur komputer yang didanai dengan baik dan bekerja untuk membuktikan atau menyangkal beberapa masalah matematika kompleks yang luar biasa (seperti P? = NP) dan mencapai hasil yang substansial hingga saat ini, kita bisa berada dalam masalah. Namun, kemajuan dalam ilmu komputer, informasi dan teori komputabilitas seperti itu tidak mungkin disembunyikan, karena fakta itu akan menulis nama-nama pencipta mereka di halaman History dan, khususnya, History of the Internet textbooks, yang tak ternilai bagi siapa pun yang cerdas . Jadi, skenario seperti itu bisa dianggap hampir mustahil.

Tidak jelas, apakah dalam 5 tahun terdekat akan ada keberhasilan dengan komputasi kuantum, meskipun sudah ada beberapa primitif kriptografi yang dianggap cocok untuk dunia pasca-kuantum: kisi-kisi, kurva elips supersingular berbasis isogeny, hash, dan kode. Untuk saat ini, spesialis keamanan hanya bereksperimen dengan mereka. Namun, tidak ada keraguan bahwa dalam hal kebutuhan, umat manusia akan dengan cepat menggunakan algoritme tersebut dalam skala massal.

Untuk saat ini, kriptografi berbasis kurva eliptik tampaknya sangat cocok untuk dekade mendatang, memberikan keamanan dan kinerja.