Bagaimana kriptografi kurva eliptik bekerja di TLS 1.3

Beberapa peringatan untuk pembaca:

Untuk (sebanyak mungkin) menyederhanakan proses penjelasan dan menekan volume publikasi, ada baiknya untuk segera melakukan reservasi kunci - semua yang kami tulis tentang sisi praktis masalah sudah benar untuk protokol TLS versi 1.3. Ini berarti bahwa meskipun sertifikat ECDSA Anda akan, jika diinginkan, bekerja dengan TLS 1.2, deskripsi proses jabat tangan, suite sandi dan tolok ukur dibuat berdasarkan versi terbaru dari protokol TLS - 1.3. Seperti yang Anda ketahui, ini tidak berlaku untuk deskripsi matematis dari algoritma yang mendasari fondasi sistem kriptografi modern.

Bahan ini tidak ditulis oleh ahli matematika atau bahkan insinyur - meskipun mereka membantu membuka jalan melalui hutan matematika. Terima kasih banyak kepada staf Qrator Labs.

( E lliptic C urve) D iffie- H ellman ( E phemeral)

Warisan Diffie-Hellman Abad 21

Tentu saja, topik ini tidak dimulai dengan Whitfield Diffie dan bukan dengan Martin Hellman. Alan Turing dan Claude Shannon membuat kontribusi besar pada teori algoritma dan teori informasi, serta ke bidang cryptanalysis. Diffie dan Hellman, pada gilirannya, secara resmi diakui oleh penulis tentang gagasan kriptografi kunci publik (juga disebut asimetris) - meskipun sekarang diketahui bahwa hasil serius di bidang ini juga telah dicapai di Inggris. Namun, mereka tetap rahasia untuk waktu yang lama - yang membuat kedua pria tersebut disebutkan dalam pelopor terjemahan.

Apa tepatnya?

Ini mungkin tampak lucu, tetapi sampai 6 November 1976, tidak ada pengetahuan yang tersedia tentang sistem kriptografi kunci publik. Whitfield Diffie dan Martin Hellman (dan, pada kenyataannya, Ralph Merkle) - matematikawan, insinyur komputer dan penggemar, serta ahli kriptologi adalah orang pertama yang mengusulkan konsep yang cocok.

Selama Perang Dunia Kedua, kriptografi membantu menjaga kerahasiaan informasi, dan analisis kriptografi membantu mengungkapkannya. Amerika Serikat dan Inggris menganggap diri mereka yang paling maju di bidang kriptografi. Kedua negara ini memasukkan algoritma kriptografi di bagian senjata dan memveto ekspor mereka. Pada saat yang sama, enkripsi yang tersedia dan dimaksudkan untuk penggunaan komersial atau rumah telah dilonggarkan di negara-negara ini. Untuk alasan ini, para peneliti Inggris yang bekerja pada skema distribusi kunci asimetris di Government Communications Center (GCHQ) dan mengembangkan konsep serupa tidak diakui oleh masyarakat sampai tahun 1997, ketika pembatasan yang ada pada algoritma kriptografi dan deskripsi mereka kehilangan semua makna dan, pada umumnya, usang secara moral.

Kembali ke pasangan penemu kami - apa yang sebenarnya dilakukan Diffie dan Hellman?

Untuk menjelaskan ini, mari kita lihat ilustrasi dari publikasi asli, yang dengan sempurna mencerminkan lompatan raksasa dalam memahami bagaimana kriptografi dapat bekerja - bahkan jika pada awalnya hanya secara teoritis:

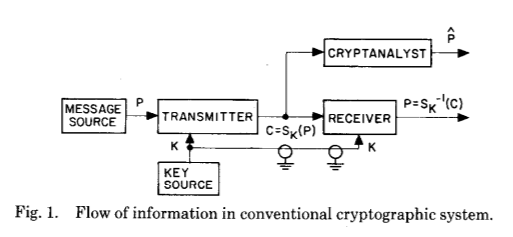
Dan sekarang untuk yang berikut:

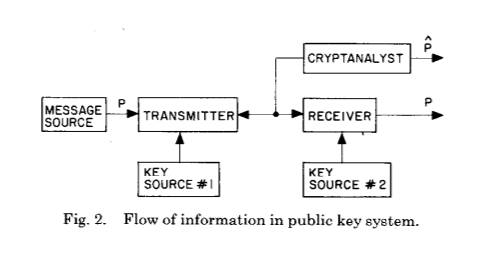
Dua gambar ini menunjukkan inovasi utama Whitfield Diffie dan Martin Hellman setelah berabad-abad pengembangan kriptografi dan kriptanalisis - pembentukan rahasia umum sebagai hasil perhitungan jenis tertentu.

Mari kita lihat gambar lain dari Wikipedia, di mana warna yang berbeda digunakan sebagai rahasia:



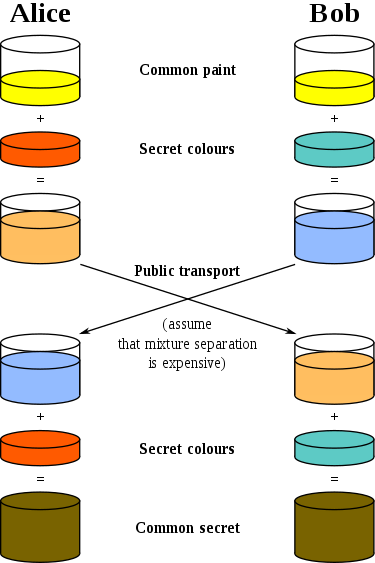
Dia juga menjelaskan dengan baik apa yang terjadi. Sebelum inovasi Diffie dan Hellman, hanya ada satu kunci bersama dalam bentuk skema pembentukan kunci bersama - digunakan untuk mengenkripsi dan mendekripsi pesan. Jika Anda ingin mentransfer kunci seperti itu ke sisi kedua, itu harus dikirim melalui saluran yang awalnya dilindungi. Semua batasan skema semacam itu segera menjadi jelas - Anda memerlukan saluran komunikasi yang aman (dari mendengarkan), Anda tidak dapat menggunakan kunci yang sama lebih dari sekali , dan, idealnya, panjang kunci harus sesuai dengan panjang pesan.

Claude Shannon, dalam karyanya yang kemudian dideklasifikasi, "Teori Komunikasi dalam Sistem Rahasia," membuktikan bahwa semua sandi yang tidak dapat dipecahkan secara teoritis harus memiliki sifat yang sama dengan blok sandi satu kali - yang juga dikenal sebagai sandi Vernam, dengan nama pencipta algoritma enkripsi aliran polyalphabetic tambahan ini.

Dan lagi, mari kita lihat publikasi ilmiah asli:


Sebelum kita melangkah lebih jauh, mari kita bertanya pada diri sendiri pertanyaan yang jelas sederhana - bagaimana mungkin dua orang, bahkan sangat berkembang secara intelektual, menghasilkan sesuatu yang begitu terobosan dalam bidang terapan, terutama mengingat keberhasilan besar masa perang? Kemungkinan besar karena kombinasi dari bidang-bidang berikut yang aktif berkembang saat itu:

• Teori Informasi yang Dirumuskan oleh Claude Shannon;
• Teori algoritma , yang dipengaruhi antara lain oleh Gereja Alonzo, John von Neumann dan Alan Turing;
• Dan, yang paling penting, teori komputabilitas , terutama didasarkan pada karya Turing.

Kita dapat mengatakan bahwa semua area ini telah berkembang dan matang sekitar periode yang sama di abad ke-20. Diffie dan Hellman juga menyebut Claude Shannon sebagai sosok yang lebih memengaruhi pekerjaan mereka daripada yang lain.

Konsep "Keamanan Universal" oleh Arjen Lenstra menunjukkan berapa banyak energi yang harus dihabiskan untuk "meretas" kriptografi simetris dengan kunci dengan panjang yang berbeda. Ternyata untuk memecahkan kunci 228-bit ke algoritma berdasarkan pada kurva eliptik, Anda membutuhkan energi sebanyak yang cukup untuk memanaskan semua air di Bumi ke titik didih. Namun, pernyataan ini benar hanya jika kita mempertimbangkan algoritma yang terkenal dan menggunakan peralatan modern, karena, secara ketat, algoritma atau peralatan yang lebih efisien adalah mungkin, tetapi keberadaannya belum diketahui. Kunci 228-bit untuk algoritma EC untuk kompleksitas peretasan sebanding dengan kunci 2380-bit di RSA, tetapi lebih banyak tentang itu nanti. Dalam perbandingan ini, kunci RSA dan EC digunakan dalam kriptosistem asimetris, mereka dapat dianggap setara dengan kunci 128-bit dalam skema simetris.

Sangat mudah untuk membayangkan bahwa sesuatu yang “sulit untuk dihitung” akan membutuhkan banyak waktu dan energi untuk menghitung. Kita cenderung berpikir bahwa komputer dapat "menghitung apa saja," tetapi ternyata ini jauh dari kebenaran.

Pertama, ada contoh masalah yang tidak dapat diselesaikan, seperti masalah berhenti. Namun, di bidang kriptografi tugas seperti itu tidak digunakan.

Kedua, jika kita mempertimbangkan runtime yang diperlukan oleh algoritma tertentu, maka itu bisa menjadi besar secara sewenang-wenang. Inilah yang digunakan kriptografi. Suatu tugas dianggap “sederhana” secara komputasi jika waktu yang dibutuhkan untuk algoritma yang sesuai untuk bekerja tergantung pada ukuran data input (diukur dalam bit) sebagai polinomial: $$$T (n) = O (n ^ k)$ untuk beberapa positif $$$k$ . Dalam teori kompleksitas komputasi, masalah seperti itu membentuk kelas kompleksitas P. Jika waktu berjalan algoritma tumbuh lebih cepat daripada polinomial, misalnya, secara eksponensial, maka tugas seperti itu dianggap komputasi "sulit".

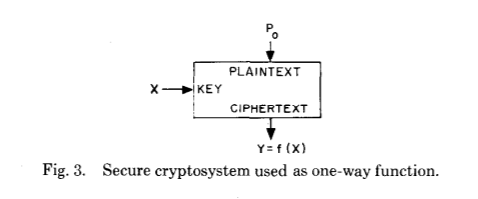
Kompleksitas kelas P mencakup tugas-tugas yang ada algoritma deterministik yang bekerja dalam waktu polinomial. Kelas kompleksitas lainnya adalah NP (di mana, mungkin, "sulit" masalah ada), yang merupakan masalah solvabilitas - yaitu, masalah yang membutuhkan jawaban "ya" atau "tidak", kebenaran solusi yang dapat diperiksa - yaitu, untuk memberikan bukti kebenaran solusi - dalam waktu polinomial. Lihat kata "bukti" di sini? Ini adalah tempat di mana kita beralih ke fungsi satu sisi yang masalah inversinya milik NP kelas kompleksitas.


Diposting oleh: xkcd

(Fungsi satu arah (dengan input rahasia))

Menurut definisi, fungsi satu arah adalah fungsi yang mudah untuk menghitung input apa pun, tetapi sulit untuk membalikkan, yaitu, mendapatkan input asli dengan hanya hasilnya. "Mudah" dan "keras" merujuk pada teori kompleksitas komputasi yang disebutkan di atas. Sangat menarik bahwa keberadaan fungsi satu arah (secara matematis) belum dibuktikan, karena bukti kuat keberadaan mereka juga akan membuktikan ketidaksetaraan kelas P dan NP, salah satu masalah milenium dan masalah terbuka yang mendesak, yang solusinya menjanjikan terobosan algoritmik. Karena itu, perlu diingat bahwa hampir semua kriptografi modern didasarkan pada hipotesis yang tidak terbukti.

Dalam publikasi aslinya, Diffie dan Hellman memperkenalkan generasi baru fungsi satu arah, menyebut mereka "fungsi satu arah dengan input rahasia" - dalam fungsi pintu jebakan bahasa Inggris. Bagaimana mereka berbeda dari fungsi satu arah saja?

Mari kita lihat penjelasan aslinya:

Dalam cryptosystem dengan kunci publik, enkripsi dan dekripsi dilakukan oleh berbagai kunci - E dan D, masing-masing, sehingga komputasi D dari E praktis tidak mungkin (misalnya, membutuhkan $$$10 ^ {100}$ instruksi). Kunci enkripsi E dapat diungkapkan kepada publik tanpa mengurangi kunci D. Ini memungkinkan pengguna sistem untuk mengirim pesan ke pengguna lain, dienkripsi sedemikian rupa sehingga hanya penerima yang diharapkan dapat mendekripsi itu. <...> Tugas otentikasi, mungkin, adalah masalah telekomunikasi yang lebih serius untuk transaksi bisnis, dibandingkan dengan distribusi kunci, karena itu (otentikasi) terletak di jantung setiap sistem yang bekerja dengan kontrak dan penagihan pembayaran.

Biasanya, karakter kriptografi Alice dan Bob digunakan untuk menjelaskan prinsip-prinsip operasi cryptosystem (mereka berusaha untuk komunikasi yang aman). Alice dan Bob setuju untuk memilih bilangan prima besar $$$n$ dan $$$g$ sedemikian rupa $$$1 <g <n$ . Pilihan ini memengaruhi keamanan seluruh sirkuit. Nomor $$$n$ disebut modul harus sederhana; apalagi, jumlahnya $$$(n-1) / 2$ seharusnya juga sederhana, tetapi $$$g$ harus menjadi akar primitif dalam kelompok modulo residu $$$n$ ; sebagai tambahan $$$n$ harus cukup besar - setidaknya 512 bit dalam representasi biner. Lebih lanjut, protokol Diffie-Hellman dapat dijelaskan dalam lima langkah sederhana:

1. Alice mengambil $$$x$ (prime besar) dan menghitung $$$X = g ^ x \ bmod n$
2. Bob mengambil $$$y$ (juga prima besar) dan menghitung $$$Y = g ^ y \ bmod n$
3. Alice mengirim $$$X$ Bob, Bob mengirim $$$Y$ Alice ( $$$x$ dan $$$y$ masing-masing tetap rahasia)
4. Alice menghitung $$$k = Y ^ x \ bmod n$
5. Bob sedang menghitung $$$k '= X ^ y \ bmod n$

Alhasil, Alice dan Bob mendapatkan hasil yang sama dalam konstruksi. $$$k = k '$ - rahasia bersama.

Jadi, fungsi satu arah dengan input rahasia adalah fungsi satu arah yang dapat dibalik dengan memiliki informasi khusus yang disebut "input rahasia". Kedengarannya sederhana, tetapi dalam praktiknya, menemukan fungsi seperti itu ternyata bukan tugas sepele - metode pertama yang layak ternyata adalah nenek moyang dari seluruh keluarga algoritma berdasarkan kunci publik yang disebut RSA dengan nama penciptanya: Ron Rivesta, Adi Shamira dan Leonard Adleman.

RSA

Dalam RSA, kompleksitas pembalik suatu fungsi didasarkan pada fakta bahwa faktorisasi (faktorisasi suatu angka) membutuhkan waktu lebih lama daripada perkalian atau, lebih tepatnya, dapat dikatakan bahwa tidak ada metode untuk memfaktorkan jumlah besar dalam waktu polinomial yang ditemukan pada komputer klasik, meskipun tidak Terbukti bahwa algoritma semacam itu tidak ada.

Di RSA, seperti dalam sistem kriptografi lainnya dengan kunci publik, ada dua kunci: publik dan pribadi. Algoritma RSA mengambil pesan input yang diwakili oleh string bit dan menerapkan operasi matematika untuknya (menaikkan ke modulo daya sejumlah besar) untuk mendapatkan hasil yang tidak dapat dibedakan dari acak. Untuk dekripsi, hasilnya diambil dan operasi serupa dilakukan untuk menerima pesan asli. Dalam kriptografi asimetris, enkripsi dilakukan dengan kunci publik, dan dekripsi dengan kunci pribadi.

Bagaimana ini mungkin? Karena kenyataan bahwa nilai-nilai yang digunakan milik kelompok siklik terbatas (himpunan bilangan bulat dengan perkalian dalam aritmatika modular). Komputer tidak bekerja dengan sangat baik dengan jumlah besar yang sewenang-wenang, tetapi properti dari grup siklik adalah "membungkus" - angka yang lebih besar dari maksimum yang diizinkan "dibungkus" ke nilai dari set yang diizinkan. Ini memungkinkan kita untuk menggunakan kunci dengan panjang "tidak lebih dari" sejumlah bit. Dalam kriptografi berdasarkan kurva eliptik, kelompok siklik (multiplikatif) juga digunakan, tetapi dikonstruksi sedikit berbeda, seperti yang akan kita lihat nanti.

Pada tingkat yang sangat primitif, semua RSA lakukan adalah mengambil dua bilangan prima besar, mengalikannya untuk mendapatkan apa yang disebut modul. Semua angka lain yang dengannya operasi akan dilakukan harus antara nol dan nilai modul. Modul itu sendiri akan menjadi bagian dari kunci publik - panjangnya menentukan panjang kunci. Bagian kedua dari kunci publik adalah angka yang dipilih antara nol dan nilai fungsi Euler (implementasi RSA modern menggunakan fungsi Carmichael alih-alih Euler) dari modul, dengan beberapa batasan tambahan. Akhirnya, Anda bisa menghitung kunci privat dengan menyelesaikan persamaan modular. Untuk mengenkripsi pesan, kami mengambil nomor yang mewakili pesan dan hanya menaikkannya ke kekuatan yang sama dengan nilai kunci publik, dan untuk mendekripsi - untuk menerima pesan asli, naikkan ke kekuatan yang sama dengan nilai kunci pribadi. Karena sifat siklus grup, kami mendapatkan makna yang sama.

Saat ini, RSA memiliki dua masalah utama, salah satunya adalah konsekuensi dari yang lain. Saat panjang kunci tumbuh, kompleksitas tidak tumbuh secepat yang kita inginkan. Ini karena ada algoritma faktorisasi subeksponensial (tetapi masih superpolinomial ). Oleh karena itu, untuk mempertahankan tingkat perlindungan yang diperlukan, panjang kunci RSA harus tumbuh agak lebih cepat daripada kunci ECC. Untuk alasan ini, panjang kunci RSA yang paling umum saat ini cukup besar: 2048 dan 3072 bit.

Beberapa saat kemudian kita akan melihat pada angka-angka spesifik bagaimana panjang kunci mempengaruhi kinerja akhir cryptosystem dengan membandingkan sertifikat yang ditandatangani oleh Let's Encrypt RSA dan ECDSA.

E lliptic C urve Digital S ignature A lgorithms

Dalam mencari fungsi yang lebih dapat diandalkan dengan input rahasia, pada pertengahan 80-an cryptographers datang untuk menggunakan cabang matematika yang dikhususkan untuk kurva elips.

Akan terlalu sulit untuk menggambarkan semua detail kriptografi berdasarkan kurva eliptik dalam satu teks, jadi kami tidak akan melakukan ini. Sebagai gantinya, mari kita lihat fungsi input rahasia satu arah yang dibangun berdasarkan kurva eliptik dan masalah logaritma diskrit.

Ada sejumlah besar bahan ulasan dan pengantar yang lebih rinci untuk bidang kriptografi ini. Kami ingin menunjukkan "ECC: pengantar lembut" oleh Andrea Corbellini, terutama jika Anda tertarik pada perangkat.

Kami, dalam materi ini, tertarik pada penjelasan yang “lebih sederhana”.
Kurva elips didefinisikan oleh persamaan yang terlihat seperti ini: $$$y ^ 2 = x ^ 3 + kapak + b$ .

Objek kedua adalah subkelompok siklik di atas bidang hingga. Parameter berikut digunakan dalam algoritma ECC:

• Bilangan prima $$$p$ , yang menentukan dimensi bidang terakhir;
• Peluang $$$a$ dan $$$b$ persamaan kurva eliptik;
• Titik dasar $$$G$ menghasilkan subkelompok yang telah disebutkan;
• Memesan $$$n$ subkelompok;
• Kofaktor $$$h$ subkelompok.

Akibatnya, set parameter untuk algoritma kami diwakili oleh enam $$$(p, a, b, G, n, h)$ .

Poin dari kurva eliptik milik bidang terbatas $$$\ mathbb {F} _p$ dimana $$$p$ ini adalah bilangan prima yang cukup besar. Jadi, kami memiliki banyak bilangan bulat modulo $$$p$ di mana operasi seperti penambahan, pengurangan, penggandaan, mengambil yang sebaliknya adalah mungkin. Penambahan dan perkalian bekerja dengan cara yang mirip dengan bagaimana kami menggambarkan ini dalam hal aritmatika modular bagian RSA (membungkus).

Karena kurva simetris pada sumbu x, untuk setiap titik $$$P$ kita bisa ambil $$$−P$ dan mendapatkan titik yang berlawanan dengannya. Kami segera menetapkan bahwa intinya $$$−O$ sesuai dengan nol, yaitu $$$−O$ akan sederhana $$$O$ .

Penambahan titik pada suatu kurva didefinisikan sedemikian rupa sehingga, mengetahui titik-titik tersebut $$$P$ dan $$$Q$ , kita bisa menggambar garis melewati kedua titik ini, serta yang ketiga - $$$R$ jadi itu $$$P + Q = -R$ dan $$$P + Q + R = 0$ .

Mari kita lihat ilustrasi ilustrasi Mark Hughes :

Kami melihat garis lurus membentang di sepanjang permukaan torus. Garis memotong dua titik yang dipilih secara acak pada kurva.



Untuk menemukan $$$R$ , kami menggambar garis dari titik yang dipilih pertama $$$P$ ke yang kedua $$$Q$ melanjutkan garis sampai melintasi kurva pada titik ketiga $$$-R$ .

Setelah persimpangan, mencerminkan titik relatif terhadap sumbu absis untuk menemukan titik $$$R$ .

Perkalian dengan skalar ditentukan dengan sangat jelas: $$$n \ cdot P = P + P + P + \ dots + P$ .

Fungsi satu arah dengan input rahasia dalam kasus ini bergantung pada masalah logaritma diskrit untuk kurva eliptik, dan bukan pada faktorisasi, seperti halnya dengan RSA. Masalah logaritma diskrit dalam hal ini dirumuskan sebagai berikut: jika diketahui $$$P$ dan $$$Q$ , lalu cara mencari $$$k$ sedemikian rupa $$$Q = k \ cdot P$ ?

Baik masalah faktorisasi (RSA yang mendasari) maupun logaritma diskrit untuk kurva eliptik (yang merupakan fondasi ECDSA dan ECDH) dianggap sulit - dengan kata lain, tidak ada algoritma untuk menyelesaikan masalah ini dalam waktu polinomial untuk panjang kunci tertentu.

Meskipun, biasanya, saya akan dibombardir dengan kain kotor (terbaik) untuk mencampur algoritma distribusi tanda tangan (ECDH) dengan tanda tangan (ECDSA), saya masih harus menjelaskan bagaimana mereka bekerja bersama.Sertifikat TLS modern berisi kunci publik, dalam kasus kami, dari pasangan yang dihasilkan menggunakan algoritma berdasarkan kurva eliptik, biasanya ditandatangani oleh beberapa organisasi yang berwenang. Klien memverifikasi tanda tangan server dan menghasilkan rahasia bersama. Rahasia ini digunakan dalam algoritma enkripsi simetris seperti AES atau ChaCha20. Namun, prinsip-prinsip dasar tetap sama: menyepakati satu set (enam) parameter, dapatkan pasangan kunci, di mana kunci pribadi adalah bilangan bulat yang dipilih secara acak (faktor$$Q = k ⋅ P ), dan kunci publik adalah titik pada kurva. Algoritma Tanda Tangan Gunakan Base Point$Q=k\cdot P$$$G , yang merupakan generator dari subkelompok pesanan$G$$$$n$ ( $$n adalah bilangan prima besar), jadi$n$$$n ⋅ G = 0 , di mana 0 adalah elemen netral dari grup. Tanda tangan membuktikan bahwa koneksi aman dibuat dengan pihak yang diautentikasi - server yang memiliki sertifikat TLS (kunci publik) yang ditandatangani oleh organisasi yang berwenang untuk nama server yang diberikan.$n\cdot G=0$

(EC) DH (E) + ECDSA = Bentuk jabat tangan modern

Dalam TLS modern versi 1.3, klien dan server menghasilkan pasangan kunci dengan cepat, membuat koneksi. Ini disebut versi "singkat" dari algoritma pertukaran kunci. Perpustakaan TLS paling populer hanya mendukung versi protokol seperti itu. Untuk sebagian besar, hari ini kurva eliptik Edwards 25519 , yang diusulkan oleh Daniel Bernstein Jr (djb), yang menyediakan tingkat perlindungan 128-bit, digunakan. Sejak 2014, kurva ini telah tersedia untuk membuat pasangan kunci di pustaka openssh. Namun, pada akhir 2019, browser masih belum membuat sesi TLS dengan server menggunakan kunci publik untuk algoritma tanda tangan EdDSA.

Mari kita lihat bagaimana semuanya bekerja di TLS 1.3.

Dalam versi terbaru dari protokol, mekanisme distribusi kunci terbatas pada (EC) DH (E) - x25519 adalah fungsi yang paling umum untuk mendapatkan kunci bersama - didukung oleh sebagian besar perpustakaan dan server perpustakaan TLS. Suite sandi hanya terdiri dari tiga entri: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 dan TLS_CHACHA20_POLY1305_SHA256. Bagi Anda yang akrab dengan bagaimana cipher suites diberi nama dalam versi protokol sebelumnya - TLS 1.2, jelas bahwa indikasi mekanisme pertukaran kunci "terpisah" dari cipher suite selama transisi ke TLS 1.3. Juga, metode pertukaran kunci RSA dan DH statis dikeluarkan dari spesifikasi. Bahkan pemulihan sesi di TLS 1.3 dengan bantuan PSK dan tiket sesi sebelumnya berlangsung sesuai dengan protokol ECDHE, di mana E-ephemerality terakhir sangat penting.Juga, dalam TLS 1.3, tidak mungkin untuk menetapkan nilai Anda sendiri untuk mekanisme Diffie-Hellman - hanya satu set yang telah ditetapkan yang tersisa dalam spesifikasi protokol, ada konsensus mengenai keamanan set ini.

Yang menarik adalah fakta bahwa mekanisme enkripsi asimetris modern bekerja secara berbeda. Dalam ECC (khususnya, ketika menggunakan sertifikat ECDSA) kami menggunakan kunci yang relatif pendek dibandingkan dengan RSA untuk mencapai tingkat keamanan yang dapat diterima. Ini memungkinkan Anda untuk menggunakan kriptografi asimetris yang kuat dan skema pertukaran kunci bahkan pada perangkat yang, tampaknya, seharusnya tidak memiliki daya yang cukup untuk operasi yang diperlukan - misalnya, kartu pintar.

Pertama, perlu untuk mengklarifikasi apa arti istilah "cryptosystem hybrid" sebagaimana berlaku untuk deskripsi TLS 1.3. Hybrid cryptosystem menggunakan skema enkripsi asimetris (dengan kunci publik) untuk membangun rahasia bersama, yang kemudian digunakan sebagai kunci dalam blok simetris atau algoritma enkripsi aliran.

Kedua, ada infrastruktur kunci publik (PKI) dan sertifikat (CA). Sangat menarik bahwa pada tahun 2004 Martin Hellman menyebutkan salah satu dari "pahlawan tanpa tanda jasa" - Lauren Könfelder, yang tesisnya untuk mempertahankan diploma sarjana MIT adalah kemungkinan menciptakan struktur pohon - yang sekarang kita kenal sebagai PKI. Tapi mari kita kembali ke sertifikat.

Fakta bahwa server benar-benar memiliki kunci pribadi diverifikasi oleh tanda tangannya, yang dapat diverifikasi menggunakan kunci publik. Dan file sertifikat di server menyatakan bahwa kunci publik tertentu milik server tertentu. Ini berarti bahwa Anda membuat koneksi yang aman dengan lawan bicara yang diinginkan, dan bukan penipu - bank Anda, bukan penipuan cyber.

TLS 1.3 telah secara signifikan meningkatkan skema negosiasi dibandingkan dengan versi protokol sebelumnya. Sekarang server menandatangani semua informasi yang diterima di jabat tangan pada saat tanda tangan dibuat: client halo dan server sendiri halo bersama dengan set cipher yang dipilih untuk digunakan. Mari kita lihat bagian yang sesuai dari deskripsi interaksi dari RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

Dalam TLS 1.3, klien mengirimkan bagian kunci (beserta parameter yang diperlukan) dan daftar tanda tangan yang tersedia di pesan pertama (Klien Halo). Kunci yang diperlukan pada tahap ini dibuat oleh klien saat itu juga - pengguna bahkan tidak menyadari hal ini. Selanjutnya, klien dan server bertukar informasi ini untuk membuat rahasia bersama - kunci sesi yang dibuat (atau, lebih tepatnya, diturunkan) dari pasangan pra-master yang diterima setelah server merespons klien dengan pesannya (Server Hello).
Di sisi "Server Halo", Anda dapat melihat catatan terkait dengan transfer sertifikat ke klien (Sertifikat *), bersama dengan cek CertificateVerify *, yang mengonfirmasi bahwa pihak tersebut benar-benar memiliki kunci pribadi terkait dengan catatan kunci publik yang sesuai, kemudian membuat pasangan kunci sesi (simetris) di kasus kesuksesan. Dengan kata lain, pihak yang meminta data (klien) telah berhasil memverifikasi keaslian pihak yang merespons (server) dengan beralih menggunakan rahasia bersama.

Dua operasi kriptografi utama dilindungi dalam transfer ini - membuat tanda tangan dan memverifikasi tanda tangan. Operasi ini biasanya dilakukan di berbagai ujung koneksi, karena paling sering klien memverifikasi keaslian server. Tanda tangan pada dasarnya adalah konfirmasi kepemilikan kunci pribadi yang sesuai dengan kunci publik. Yaitu, bahwa kami menerima data dari penandatangan, dan memastikan bahwa pesan itu tidak berubah selama transfer.

Saat menggunakan algoritme RSA, karena kami akan menunjukkan sedikit lebih lanjut tentang angka, operasi membuat tanda tangan adalah yang paling mahal. Karena kami menandatangani dengan kunci 2048 atau 3072-bit, operasi semacam itu secara signifikan memuat server - jauh lebih kuat daripada klien selama verifikasi (tanda tangan).

Dalam ECDSA, kami beroperasi dengan kunci yang relatif pendek (dalam contoh benchmark, kita akan melihat ECDSA menggunakan kurva NIST P-256 (atau secp256v1), tetapi kunci ini terlibat dalam operasi yang lebih kompleks. Akibatnya, menggunakan ECC dapat direpresentasikan sebagai RSA “terbalik” dengan sudut pandang kinerja: klien dimuat jauh lebih berat oleh operasi verifikasi penandatanganan, sementara server dengan mudah menangani operasi pembuatan tanda tangan, yang dikonfirmasi oleh pengukuran yang kami berikan di bagian benchmark.

Efek ini membantu meningkatkan skala Internet - karena klien modern hampir sama kuatnya dengan server (jika kita hanya mempertimbangkan kecepatan clock dari inti prosesor), mereka dapat secara efektif melakukan operasi yang sulit secara komputasi tanpa masalah. Server, pada gilirannya, dapat menggunakan daya komputasi yang dibebaskan untuk membuat lebih banyak tanda tangan dan, sebagai hasilnya, membuat lebih banyak sesi.

Tanda Tangan Sertifikat di Let's Encrypt

Kami akan memberikan pembaca kami dengan instruksi yang sederhana dan dapat dipahami di mana Anda dapat secara mandiri membuat server yang mampu membangun sesi TLS menggunakan pasangan kunci ECDSA di mana Let's Encrypt ditandatangani secara publik dan termasuk dalam sertifikat rantai perwalian sebagai sertifikat.
Kami memutuskan untuk menunjukkan jalur lengkap dari membuat kunci, membuat permintaan penandatanganan sertifikat (CSR) untuk Let's Encrypt dan mengirimkannya untuk ditandatangani menggunakan utilitas certbot, yang mengembalikan rantai yang diperlukan dan sertifikat ECDSA itu sendiri.

Pertama, Anda perlu membuat pasangan kunci. Untuk ini kita akan menggunakan pustaka OpenSSL. Panduan Pengguna OpenSSL mengatakan bahwa membuat kunci untuk algoritma berdasarkan kurva eliptik terjadi menggunakan perintah khusus yang didedikasikan untuk keluarga algoritma berdasarkan kurva eliptik.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

Untuk memverifikasi bahwa tim kami bekerja dengan benar, kami menjalankan perintah ec yang menunjukkan jalur ke file yang baru dibuat yang berisi kunci pribadi.

 openssl ec -in privatekey.pem -noout -text 

Keluaran harus menunjukkan kepada kita kurva yang digunakan, yang dengannya kunci dihasilkan.

Langkah selanjutnya cukup penting ketika membuat CSR - agar tidak mengisi kuesioner yang diperlukan untuk menandatangani sertifikat setiap kali, kita memerlukan file konfigurasi. Untungnya, hampir semua pekerjaan untuk kami dilakukan oleh Mozilla, menciptakan " Generator Konfigurasi SSL ". Di dalamnya, Anda dapat memilih dari berbagai opsi untuk mode server yang dengannya Anda dapat membuat koneksi TLS. Konfigurasi OpenSSL yang bersih, untuk beberapa alasan hilang dari generator Mozilla, terlihat seperti ini:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

Catatan: Anda tidak harus memiliki file konfigurasi - jika tidak ada di sana, Anda akan diminta untuk mengisi semua bidang pada baris perintah. Dengan file konfigurasi, jalur yang kita tentukan dalam perintah berikutnya, prosesnya disederhanakan.

Berikutnya adalah pembuatan permintaan penandatanganan sertifikat (CSR) itu sendiri. Untuk ini, kami memiliki tim OpenSSL yang nyaman.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

Kami juga dapat memverifikasi kebenaran CSR yang baru dibuat.

 openssl req -in csr.pem -noout -text -verify 

Akhirnya, kami sampai pada tahap akhir - menggunakan klien ACME, certbot, kami akan mentransfer permintaan kami untuk menandatangani sertifikat organisasi Let's Encrypt.

Certbot tidak hanya akan membantu Anda mendapatkan sertifikat, tetapi juga memiliki banyak opsi hebat lainnya. Kami menambahkan bahwa jika Anda baru mengenal kriptografi dengan kunci publik dan tidak benar-benar memahami infrastruktur kunci publik yang ada saat ini, lebih baik menggunakan opsi --dry-run sebelum mencoba untuk mendapatkan sertifikat nyata untuk setiap domain Anda.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

Dalam kasus ini, klien certbot memverifikasi bahwa daftar domain wajib yang diminta pada baris perintah cocok dengan daftar dalam permintaan penandatanganan sertifikat (CSR). Di dalam --dns-somednsprovider kami --dns-somednsprovider sedikit, karena ada banyak cara untuk mengonfirmasi Let's Encrypt bahwa Anda memiliki sebagian lalu lintas Internet. Tetapi jika Anda menggunakan beberapa jenis penyedia cloud, seperti DigitalOcean, AWS, Azure, Hetzner, apa pun - Anda mungkin sudah memiliki cara yang lebih mudah untuk memberikan informasi yang Anda butuhkan untuk sertifikasi, karena penyedia Anda telah mengurus alat integrasi.

Setelah itu, jika Anda yakin bahwa parameter yang diteruskan ke CSR menggunakan certbot ke Let's Encrypt sudah benar, hapus saja --dry-run dari perintah dan lanjutkan.

Jika berhasil, klien akan mengembalikan Anda beberapa sertifikat: sertifikat yang ditandatangani itu sendiri, sertifikat perantara dan root, serta kombinasi yang terakhir dalam bentuk rangkaian sertifikat, semua dalam format .pem.

OpenSSL memiliki perintah yang kami gunakan untuk melihat ke dalam sertifikat:

 openssl x509 -in chainfilepath.pem -noout -text 

Seharusnya sekarang menjadi jelas bahwa Let's Encrypt menandatangani sertifikat menggunakan algoritma hash SHA256. Selain itu, Let's Encrypt hanya berencana untuk menambahkan tanda tangan dan perantara ke ECDSA, jadi untuk saat ini tetap puas dengan tanda tangan RSA perantara. Tapi itu tidak menakutkan, karena bagaimanapun Anda akan menggunakan kunci publik ECDSA.

Pada akhir bagian ini, kami ingin menambahkan beberapa informasi tentang membandingkan panjang kunci berbagai algoritma. Dalam keamanan informasi, biasanya dikatakan bahwa tingkat keamanan adalah 2 ^ x, di mana x adalah panjang bit (RSA adalah pengecualian, karena ia tumbuh agak lebih lambat daripada eksponen). Untuk memperkirakan bagaimana kunci berbagai algoritma dibandingkan, kami merujuk ke halaman wiki OpenSSL :

Seperti yang Anda lihat, perbedaannya terlihat. Meskipun untuk saat ini, Let's Encrypt memungkinkan Anda untuk menerima sertifikat yang ditandatangani hanya pada kunci dua kurva elips - 256 (secp256v1) dan 384 (secp384r1).

Kesulitan yang dikenal serta NSA

Diposting oleh: xkcd

Mungkin masalah utama dalam menggunakan kriptografi berdasarkan kurva eliptik adalah perlunya generator angka acak yang diimplementasikan dengan sangat rapi, yang diperlukan untuk membuat kunci tingkat keamanan tertentu.

Skandal besar dikaitkan dengan algoritma Dual_EC_DRBG - butuh bertahun-tahun untuk menyelesaikannya. Ada ketidakpastian tentang basis paten di sekitar ECC - diketahui bahwa banyak paten milik Certicom, yang diakuisisi oleh Blackberry. Ada juga beberapa kasus sertifikasi Blackberry ECC yang dikenal. Akhirnya, ada ketidakpercayaan tertentu terhadap standar NIST, yang dapat dipengaruhi oleh NSA atau badan intelijen AS lainnya.

Kesalahan dalam penerapan standar kriptografi adalah topik yang sepenuhnya ortogonal. Pada tahun 2010, PlayStation 3 mengalami kebocoran kunci pribadi Sony karena implementasi algoritma ECDSA yang salah - Sony tidak dapat mengatasi RNG dan menyediakan nomor acak yang sama, yang memungkinkan untuk menyelesaikan fungsi dengan input rahasia. OpenSSL menderita pada tahun berikutnya, namun, dengan cepat memperbaiki kerentanan yang memungkinkannya untuk mendapatkan kunci pribadi menggunakan serangan waktu - rincian lebih lanjut dapat ditemukan di publikasi penelitian asli .

Pada konferensi RSA pada 2013, sekelompok peneliti mempresentasikan makalah penelitian berjudul " Gagal Secara Acak! ”Didedikasikan untuk kerentanan kelas Java SecureRandom. Enam bulan kemudian, segalanya dimulai dengan dompet Bitcoin yang dibuat menggunakan generator nomor acak semu yang tidak aman secara kriptografis.

Karena kenyataan bahwa beberapa kerentanan serius ditemukan dalam waktu singkat, pada Agustus 2013 yang sama, IETF merilis RFC 6979 , yang menggambarkan generasi deterministik k ketika membuat kunci. Kami dapat menulis bahwa masalahnya diselesaikan dengan cara ini, tetapi kami tidak akan - setiap saat, peneliti dapat menemukan kesalahan baru dalam implementasi karena penyimpangan yang tidak perlu dari spesifikasi protokol.

Dan beberapa kata tentang NSA. Jika Anda belum mengetahui riwayat Dual_EC_DRBG - luangkan waktu dan membaca materi yang relevan, Anda tidak akan menyesal bahwa Anda telah mengetahui detailnya. Edward Snowden menjadi bagian dari cerita ini, karena itu karena kebocorannya pada tahun 2013 semua keraguan yang ada dikonfirmasi. Ini menghasilkan fakta bahwa banyak cryptographers terkemuka kehilangan kepercayaan pada NIST, karena organisasi inilah yang menciptakan dan mendeskripsikan banyak kurva eliptik dan algoritma yang bekerja di ECDSA.

Kurva 25519 yang ditulis oleh Daniel Burnshite dan fungsi Diffie-Hellman untuk distribusi kunci adalah jawaban untuk banyak pertanyaan di atas. Dan, seperti yang sudah kami tulis, ada gerakan stabil menuju EdDSA. Dalam kasus kurva NIST, belum ada konfirmasi kerentanan mereka telah ditemukan, dan untuk pengalaman dengan angka acak, itu agak menyakitkan dan berkontribusi pada asimilasi cepat.

Untuk mengakhiri bagian ini, kami ingin mengutip John von Neumann: "Siapa pun yang memiliki kelemahan untuk metode aritmatika untuk mendapatkan angka acak tidak berdosa tanpa keraguan."

Beberapa tolok ukur

Kami menggunakan server NGINX 1.16.0 dengan pustaka OpenSSL versi 1.1.1d untuk melakukan pengujian dengan dua sertifikat. Seperti yang disebutkan sebelumnya, pada saat ini, Let's Encrypt memungkinkan Anda untuk hanya menggunakan algoritma prime256v1 dan secp384r1 untuk membuat permintaan penandatanganan sertifikat, serta tidak memberikan sertifikat EPCSA root dan perantara dengan tanda tangan, mungkin berurusan dengan fitur ini saat Anda membaca catatan ini.

Seperti yang Anda lihat, pada satu inti CPU Intel® Xeon® Silver 4114 @ 2.20GHz (dirilis pada kuartal ketiga 17), perbedaan total antara kinerja ECDSA dan RSA yang diterima secara umum dengan panjang kunci 2048 bit adalah 3,5 kali.

Mari kita lihat hasil menjalankan perintah openssl -speed untuk ECDSA dan RSA pada prosesor yang sama.

Di sini kita dapat menemukan konfirmasi dari tesis yang ditulis sebelumnya tentang bagaimana operasi komputasi dari tanda tangan dan verifikasi berbeda antara ECC dan RSA. Saat ini, dipersenjatai dengan TLS 1.3, kriptografi berdasarkan kurva eliptik memberikan peningkatan yang signifikan dalam kinerja server dengan tingkat perlindungan yang lebih tinggi dibandingkan dengan RSA. Ini adalah alasan utama mengapa kami di Qrator Labs merekomendasikan dan sangat mendorong pelanggan yang siap untuk menggunakan sertifikat ECDSA juga. Pada CPU modern, peningkatan kinerja yang mendukung ECDSA adalah 5x.

Jika Anda tertarik pada bagaimana prosesor (rumah atau server) Anda menangani komputasi kriptografi, jalankan perintah kecepatan openssl. Opsi -rsa , -ecdsa dan -eddsa memungkinkan Anda menentukan algoritme yang menarik untuk pembandingan.

Masa depan (dalam superposisi)

Ironisnya, dalam proses penulisan materi ini, Google mengumumkan "mencapai keunggulan kuantum . " Apakah ini berarti bahwa kita sudah dalam bahaya dan semua kemajuan yang dibuat untuk saat ini tidak lagi dapat memastikan kerahasiaan?

Tidak.

Seperti Bruce Schneier menulis dalam esai "Kriptografi setelah Pendaratan Asing" untuk IEEE Security and Privacy Circular, komputer kuantum dapat benar-benar memberikan pukulan serius hanya pada kriptografi asimetris dengan kunci publik. Algoritma simetris akan tetap bertahan.

Namun untuk melanjutkan, kami akan memberikan kesempatan kepada Tn. Schneier sendiri:

Ada skenario masa depan lain yang tidak memerlukan komputer kuantum. Sementara kami sekarang memiliki beberapa teori matematika yang mendasari keberpihakan yang digunakan dalam kriptografi, bukti validitas teori-teori ini sebenarnya adalah salah satu masalah terbuka terbesar dalam ilmu komputer. Sama seperti kriptografer pintar dapat menemukan trik baru yang memfasilitasi peretasan algoritma tertentu, kita dapat membayangkan alien dengan teori matematika yang cukup untuk memecahkan semua algoritma enkripsi. Hari ini rasanya konyol. Kriptografi kunci publik adalah sejumlah teori dan berpotensi rentan terhadap alien yang berpikiran matematika. Kriptografi simetris begitu non-linier, begitu sederhana untuk dibuat dan rumit, dan juga betapa mudahnya untuk memperpanjang kunci, masa depan yang tak terbayangkan. Contohnya adalah varian AES dengan ukuran blok dan kunci 512-bit, serta 128 putaran. Jika matematika secara fundamental tidak berbeda dari pemahaman kita saat ini, maka algoritma seperti itu akan aman sampai komputer terbuat dari sesuatu selain materi dan menempati sesuatu selain ruang.

Tetapi jika hal yang tidak dapat dibayangkan terjadi, itu akan meninggalkan kita hanya dengan kriptografi yang hanya didasarkan pada teori informasi: cipher-notes sekali pakai dan variannya.

Bruce Schneier dengan sempurna menggambarkan area di mana, selain kesalahan implementasi, kerentanan utama kriptografi modern dapat ditemukan. Jika di suatu tempat ada sekelompok ahli matematika, cryptanalysts dan cryptographers, bersama dengan insinyur komputer bekerja pada bukti atau sanggahan dari beberapa masalah matematika yang sangat kompleks (seperti P? = NP), yang telah berhasil mencapai beberapa kemajuan dalam kegiatan ini saat ini - posisi kita rentan. Dengan menolak teori konspirasi, dapat dikatakan bahwa kemajuan semacam itu dalam bidang ilmu komputer, teori informasi, dan teori komputabilitas sulit disembunyikan. Peristiwa semacam itu akan memasukkan nama-nama pencipta mereka sendiri di halaman Sejarah dan, khususnya, dalam buku-buku Sejarah Internet, yang sangat berharga bagi individu atau kelompok yang sangat cerdas. Jadi skenario yang sama dapat dibuang sebagai tidak mungkin.

Juga tidak jelas apakah keberhasilan dalam komputasi kuantum akan dibuat dalam 5 tahun ke depan - dan sudah ada primitif kriptografi yang cocok untuk digunakan di dunia pasca-kuantum: kisi-kisi, menggunakan isogenisasi supersingular dari kurva eliptik, fungsi hash, kode koreksi kesalahan. Sekarang, pakar keamanan hanya bereksperimen dengan mereka, tetapi tidak ada keraguan bahwa, jika perlu, umat manusia akan menemukan cara untuk dengan cepat menggunakan algoritma baru pada skala apa pun.

Tetap hanya menambahkan bahwa untuk dekade berikutnya, kriptografi berdasarkan kurva elips tampaknya cocok untuk tujuan dan kebutuhan yang sebagian besar penggunanya tetapkan untuk diri mereka sendiri, memberikan keamanan dan kinerja tinggi.