Mengubah, mengatur ulang dan menurunkan urutan bentuk yang telah ditentukan, Algoritma Printer Tetris menggunakan mekanika Tetris untuk menghasilkan bitmap yang sewenang-wenang.
Deskripsi algoritma
Algoritma mengubah piksel gambar sumber ke dalam kotak dari bidang
Tetris baris demi baris, bergerak dari bawah ke atas. Untuk menghasilkan persegi tunggal, algoritma ini menyusun struktur yang terdiri dari area persegi panjang yang sepenuhnya didukung oleh satu persegi di bawahnya. Setelah perakitan wilayah persegi panjang selesai, garis-garisnya dibersihkan, meninggalkan satu persegi di bawahnya. Berikut adalah tiga contoh perilaku ini.
Seperti yang ditunjukkan di bawah ini, algoritma juga dapat menghasilkan beberapa kotak dengan satu struktur.
Dalam proses membangun baris, semua kotak yang dibuat dengan cara ini harus didasarkan pada sesuatu. Pada gambar yang ditunjukkan di atas, kotak yang dihasilkan berada di lantai lapangan bermain. Namun, jika garis arbitrer berisi lubang, maka itu tidak akan dapat memberikan dukungan yang diperlukan untuk membangun garis di atasnya. Algoritma memecahkan masalah ini dengan membuat platform datar di atas string berlubang. Dalam animasi di bawah ini, platform yang dibangun di atas garis terdiri dari satu kotak merah. Platform adalah struktur sementara, dan memasukkan bentuk terakhir akan menghapusnya.

Baris 5 kotak merah yang ditunjukkan di bawah ini berada di atas baris 3 kotak merah. Ini diwujudkan dengan membangun platform datar di atas garis bawah. Platform ini menyediakan dukungan yang dibutuhkan untuk menghasilkan 5 kotak merah. Pada akhirnya, platform dihapus dengan memasukkan bentuk terakhir, dan baris baru jatuh ke tempatnya. Perhatikan bahwa jika algoritma perlu menghasilkan garis dalam urutan terbalik (garis 3 kotak merah di atas garis 5 kotak merah), maka platform tidak akan diperlukan.
Satu Pola Kotak
Untuk referensi, saya akan memberikan nama 7 tetramino (potongan game).
Versi Tetris Printer Algorithm yang disajikan dalam artikel ini dirancang khusus untuk merender sprite dari video game lama. Gim-gim ini mengemas gambar dalam 8 × 8 ubin, dan 2 byte dialokasikan untuk setiap piksel. Karena itu, sprite biasanya hanya berisi 3 warna plus area transparan dan paling sering memiliki ukuran 16 × 16 atau 16 × 32 piksel.
Animasi di bawah ini menunjukkan semua pola yang digunakan untuk membuat kotak individu. Setiap pola menggunakan tetramino J, T, dan L yang dapat dipertukarkan, menciptakan satu kotak di bagian bawah. Algoritma ini menetapkan tetramino ini ke salah satu dari 3 warna yang ada dalam sprite. Sisa tetramino diberi warna sewenang-wenang. Sepanjang permainan, semua warna tetap konstan.
Karena bentuk tiga tetramino, tidak mungkin untuk membuat kotak dari ketiga warna di dua pertama dan dua terakhir kolom. Oleh karena itu, lebar minimum bidang bermain untuk merender sprite dengan lebar 16 piksel adalah 2 + 16 + 2 = 20 kotak. Namun, ternyata 20 terlalu sedikit.
Seperti yang ditunjukkan di bawah ini, area di atas alun-alun tunggal tidak dapat terdiri dari hanya satu garis, karena satu-satunya angka yang dapat masuk di dalamnya (tetramino I) tidak memiliki dukungan.
Dengan dua garis, satu-satunya cara untuk merentangkan seluruh lapangan bermain sehingga memiliki dukungan adalah dengan menggunakan tetramino S dan Z. Tetapi dalam kasus ini, lubang akan tetap berada di baris atas.
Jumlah minimum garis yang diperlukan di atas kotak paling bawah adalah 3, dan seperti yang ditunjukkan beberapa kali di atas, pola tersebut ada. 20 kotak adalah lebar minimum yang diperlukan untuk menempatkan sprite dengan lebar 16 piksel. Tetapi 20 × 3 + 1 = 61, dan angka ini tidak habis dibagi 4, yang berarti tidak dapat dibangun dari tetramino. Namun, lebar 21 memberi kita 21 × 3 + 1 = 64, dan dapat dibangun dari 16 tetramino. Bahkan, lebar ini memungkinkan algoritma untuk membuat sprite hingga 17 piksel lebar.
Lapangan bermain Tetris asli memiliki ukuran 10 × 20 kotak (rasio 1: 2). Rasio ini dipertahankan dalam versi algoritma ini - lapangan bermain memiliki ukuran 21 × 42 kotak.
Karena tetramino J, T, dan L dapat dipertukarkan saat membuat satu kotak, dan 3 kotak dari tetramino ini terlibat dalam membuat garis di atasnya, ada 21 - 3 = 18 pola untuk membuat kotak tunggal. Namun, karena simetri cermin, sebenarnya hanya ada 9. Ada 3 garis yang bekerja untuk sebagian besar dari 9. Ini, namun sebuah studi komputer menyeluruh menunjukkan bahwa kedua pola tersebut membutuhkan lebih banyak. Opsi berikutnya yang mungkin adalah 7 baris, karena 21 × 7 + 1 = 148, yang membutuhkan 37 tetraminos. Seperti yang ditunjukkan pada gambar di bawah, ada pola seperti itu.
Berbagai Pola Kotak
Pola untuk membuat beberapa kotak terbatas pada tiga warna yang sama yang dibuat oleh pola satu kotak. Kotak yang dihasilkan dibuat dari tetramino J, T dan L, yang masing-masing menempati 3 kotak di garis di atas garis penciptaan. Jumlah kotak maksimum yang berpotensi dapat dibuat dengan pola tunggal adalah 21/3 = 7. Namun, untuk sprite dengan lebar 16 piksel, tetramino paling kanan tidak dapat membuat kotak. Bahkan dalam kasus sprite dengan lebar 17 piksel, itu dapat membuat kuadrat hanya satu warna. Oleh karena itu, pola pembuatan dari 7 kotak jarang digunakan.
Jumlah pola untuk membuat jumlah kuadrat sewenang-wenang dapat ditentukan dengan menggunakan kombinatorik enumerasi. Pertimbangkan pola di bawah ini, yang mewakili satu baris di atas deretan tiga kotak. Setiap blok dari tiga kotak putih yang berdekatan menunjuk bagian dari tetramino; kotak yang dibuat tidak ditampilkan.
Tiga tetramino membuat 4 lubang. Ada 21 - 3 × 3 = 12 kotak gelap yang dapat secara sewenang-wenang dimasukkan ke dalam rongga ini untuk membentuk pola tertentu. Jumlah cara untuk mendistribusikan kotak gelap ini dapat dihitung dengan menempatkannya pada garis di mana kotak putih tunggal diperlakukan sebagai pembagi.
Jadi, tugasnya dikurangi untuk menghitung nilai koefisien polinomial. Melihat kotak putih ini, Anda dapat memahami bahwa ini adalah pertanyaan tentang jumlah cara untuk memilih 3 dari 15.
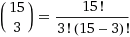
= 455.
Dalam kasus umum, untuk
n sama dengan
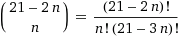
. Tetapi karena simetri cermin, pada kenyataannya, mereka setengahnya; jika kuantitasnya ganjil, kemudian membaginya dengan dua, kita membulatkan ke bilangan bulat terdekat untuk memasukkan pola simetris idealnya yang harus ada dalam set ini, seperti, misalnya, yang ditunjukkan di bawah untuk kasus dengan 455.
Menerapkan rumus ini ke 7 tetramino, kami mengkonfirmasi yang sudah jelas: hanya ada satu pola untuk membuat 7 kotak.
Pola pembuatan 6 kotak dapat dibangun dengan dua cara: dua baris diisi (2 × 21 + 6 = 48) dan enam baris diisi (6 × 21 + 6 = 132), yang membutuhkan 12 dan 33 tetramino. Rumus di atas menunjukkan bahwa ada 84 pola untuk membuat 6 kotak, tetapi hanya 35 di antaranya yang dapat dibangun dari 2 garis penuh. 49 pola membutuhkan 6 baris. Jumlahnya ganjil karena pola simetris yang ditunjukkan di bawah ini.
Perlu juga dicatat bahwa 2 garis dimungkinkan di sini, karena berbeda dengan pola pembuatan satu kotak yang membutuhkan tetramino S dan Z, 6 angka digunakan dalam pola-pola ini.
Tabel di bawah ini menunjukkan jumlah kotak yang dibuat oleh masing-masing jenis pola, jumlah garis lengkap, jumlah tetramino yang digunakan, dan jumlah pola.
Contoh pola.
Platform
Sebelum membuat garis, algoritma memeriksa garis di bawahnya. Jika baris bawah tidak dapat memberikan dukungan untuk semua kotak di atasnya, maka diperlukan platform sementara. Ketika platform dihapus, garis baru turun, dan karena bagaimana gravitasi diimplementasikan dalam Tetris asli, beberapa kotak tetap menggantung di udara.
Ilustrasi di bawah ini menunjukkan 10 pola platform. Pembangunan platform dimulai dengan menurunkan T tetramino di atas salah satu kotak dari garis yang dihasilkan terakhir. Tetraminos yang tersisa bergantung pada T. pertama ini. Yaitu, jika garis yang dihasilkan sebelumnya berisi setidaknya 1 persegi, seperti kotak merah pada gambar di bawah ini, kita dapat membuat platform datar di atasnya untuk menghasilkan baris berikutnya.
Di tengah membangun platform, garis bawah selesai dan dihapus, meninggalkan tiga baris di atasnya. Tetramino J atau L terakhir, yang akan menghapus garis-garis ini, tidak dimasukkan sampai pola pembuatan menghasilkan garis sprite berikutnya di atas platform. Gambar terakhir ini mencegah pembuatan kotak di dua baris pertama dan terakhir. Tetapi, seperti yang disebutkan di atas, karena geometri tetramino J, T, dan L yang digunakan dalam proses ini, pola untuk membuat kotak dibatasi hingga 17 kolom dalam.
Selain itu, dari 19 cara yang memungkinkan untuk membangun platform di atas Tetramino T, hanya ada 10 yang ditunjukkan di atas.
Matriks Dikemas
Seperti yang dinyatakan di atas, satu himpunan bagian dari pola penciptaan 6 kotak melibatkan hanya membersihkan dua baris. Semua pola lainnya membutuhkan 6 garis. Untuk memahami mengapa hal ini terjadi, pertimbangkan pola di bawah ini.
Tetramino ini dapat dipertukarkan dengan tetramino J dan L, dan masing-masing menambahkan 3 kotak yang berdekatan ke baris umum. Baris yang harus diselesaikan diwakili oleh matriks yang ditunjukkan di bawah ini.
Sekarang semuanya mengemas ruang kosong dengan tetramino. Mulai di sebelah kiri, satu-satunya pilihan adalah menggunakan urutan tetramino I.
Satu-satunya cara untuk mengisi ruang yang tersisa adalah dengan menggunakan J dan O atau I dan L. Kedua opsi ditunjukkan di bawah ini.
Sayangnya, tetramino O dan L tidak didukung dalam matriks yang ditunjukkan di atas. Pola 6 kotak ini membutuhkan matriks yang lebih besar.
Masalah serupa muncul dalam dua pola menciptakan satu kotak. Pertimbangkan matriks di bawah ini:
Satu-satunya cara untuk mengisi garis bawah di sebelah kanan adalah dengan rantai urutan Z.
Demikian pula, satu-satunya cara untuk mendapatkan 3 kotak kosong di kiri bawah adalah tetramino S.
Di garis tengah ada kotak kosong antara S dan Z dan satu-satunya cara untuk mengisinya adalah dengan menggunakan tetramino J, T atau L, seperti yang ditunjukkan pada gambar di bawah ini.
Memasukkan salah satu dari bentuk ini membagi ruang kosong. Area kosong di sebelah kiri masing-masing berisi 5, 6, dan 7 lubang. Karena tidak satu pun dari nilai-nilai ini yang dapat dibagi oleh 4, tidak mungkin untuk melanjutkan. Matriks yang lebih besar diperlukan untuk pola kotak tunggal ini.
Hal yang sama berlaku untuk pola lain untuk membuat satu kotak, yang ditunjukkan pada matriks di bawah ini.
Setelah menggunakan tetramino S dan Z untuk mengisi sebagian besar garis bawah, ada ruang kosong di antara mereka di garis tengah.
Seperti yang ditunjukkan pada gambar di bawah ini, sisipan lubang membagi ruang kosong, dan area kosong di sebelah kiri masing-masing berisi 9, 10, atau 11 kotak; tidak ada angka yang habis dibagi 4.
Tetapi mengepak matriks bukan satu-satunya cara untuk menghasilkan pola kotak. Misalnya, lihatlah pembuat 4 kotak di bawah ini.
Berikut ini adalah upaya untuk membuat pola sebagai satu set tetraminos paket.
L terakhir dilewati, karena ruang untuk itu terbentuk hanya setelah penyelesaian dan penghapusan baris ketiga.
Tetapi setelah pencarian menyeluruh, ditemukan bahwa teknik ini tidak memberikan pola satu-persegi yang disebutkan sebelumnya dengan kemampuan untuk bekerja hanya dengan 3 garis. Selain itu, tidak memungkinkan untuk menerapkan pola baru 6 kotak dalam dua baris. Tidak perlu mencari pola yang tersisa di luar matriks yang dikemas, karena mereka sudah menggunakan tetramino dalam jumlah sekecil mungkin. Dan membatasi diri kita pada matriks yang dikemas, kita akan menemukan semua pola yang diperlukan lebih cepat.
Pencarian Pola
Untuk menyederhanakan output data, Algoritma Tetris Printer terbatas untuk membuat tetramino di titik tengah atas bidang permainan, memutarnya, bergerak secara horizontal dan menurunkannya. Dia tidak pernah harus memindahkan sosok secara horizontal setelah melewati jarak tertentu. Pembatasan ini sangat mengurangi ruang pencarian, karena tidak memungkinkan pembentukan celah di bawah angka yang ditambahkan ke matriks. Sebagai contoh, mari kita lihat matriks 3 kotak berikut.
Jika kita melempar J di tengah matriks, seperti yang ditunjukkan di atas, maka kita mendapatkan celah 2 kotak kosong, yang tidak dapat diisi dengan angka-angka berikutnya. Karena itu, pencarian tidak akan mengikuti jalur ini.
Karena celah tertutup tidak diizinkan, setiap kolom dalam matriks dapat dianggap sebagai tumpukan kotak yang diisi dan ketinggian tumpukan ini sepenuhnya menggambarkan isi seluruh matriks. Terlepas dari jumlah baris, array integer satu dimensi dengan 21 elemen akan cukup untuk menggambarkan matriks dua dimensi.
Ketika angka jatuh ke dalam matriks, ketinggian tumpukan tumpukan kolom yang sesuai meningkat. Untuk mempercepat proses ini, semua tetramine dianalisis terlebih dahulu. Ada 19 putaran tetramino, dan pencarian menganggap masing-masing sebagai sosok yang unik.
Tetramino J di sudut kiri atas gambar menempati 3 kolom. Ketika menurunkan ke matriks, ketinggian 3 tumpukan yang berdekatan masing-masing meningkat sebesar 1, 1 dan 2 kotak. Tetapi sebelum angka dapat diturunkan, profil yang lebih rendah dari angka tersebut harus sesuai dengan profil atas tumpukan masing-masing. Jika J ini tergeletak di lantai lapangan bermain, di bawah masing-masing kolom ini seharusnya ada kesenjangan 1, 1, dan 0 kotak kosong. Karena jarak bebas dilarang, ketinggian relatif 3 tumpukan harus sepenuhnya sesuai dengan pola.
Konsekuensi lain dari kurangnya kesenjangan adalah bahwa ketika angka-angka jatuh ke dalam matriks, baris diisi dari bawah ke atas. Tidak mungkin untuk mengisi baris di tengah-tengah matriks sebelum atau tanpa menyelesaikan semua baris di bawahnya. Dalam proses mengisi matriks, batas bawahnya benar-benar bergerak ke atas. Akibatnya, tumpukan kolom matriks dapat memberikan dukungan hanya jika tingginya minus jumlah baris selesai lebih besar dari 0. Ketika suatu bentuk ditambahkan ke matriks, setidaknya salah satu kolom yang sesuai harus memberikan dukungan.
Pencarian menyimpan array satu dimensi kedua yang berisi jumlah kuadrat terisi di setiap baris. J di atas berisi dalam baris yang sesuai 3 dan 1 a persegi. Ketika Anda memasukkannya ke dalam matriks, nilai-nilai ini ditambahkan ke elemen array yang sesuai. Jumlah garis yang diselesaikan adalah jumlah elemen dengan nilai 21.
Seperti yang dinyatakan pada bagian sebelumnya, jika angka yang ditambahkan membagi matriks, maka ukuran area yang dihasilkan harus dibagi dengan 4. Misalnya, pada gambar di bawah ini, menambahkan I membuat 2 area, yang masing-masing berisi 46 kotak kosong. Karena 46 tidak dapat dibagi dengan 4, tidak ada lagi cara untuk mengisi sisa matriks.
Pemisahan muncul ketika ketinggian tumpukan sama dengan ketinggian matriks. Setelah memasukkan gambar dengan menambah ketinggian tumpukan masing-masing, dimensi dari semua area ruang kosong dapat ditentukan dengan memindai array ketinggian dan menambahkan ruang yang tersisa di setiap tumpukan. Nomor ini dicentang dan disetel ulang ketika suatu perpecahan terdeteksi.
Pencarian yang digunakan untuk menghasilkan semua pola menggunakan konstruksi inkremental acak, algoritma penelusuran balik yang secara sistematis memeriksa semua kombinasi dalam urutan acak. Konstruksi inkremental dari suatu solusi dengan memasukkan bentuk secara acak membuatnya tumbuh seperti kristal. Keacakan menyediakan ketidakberaturan yang mengandung wajah pecah yang berfungsi sebagai dasar untuk bentuk selanjutnya yang ditambahkan. Sebagian besar matriks dikemas secara acak dengan sangat cepat, dan ketika ruang kosong menjadi langka, backtracking ikut bermain.
Sebelum melakukan pencarian, permutasi acak dari 371 cara menambahkan angka ke matriks dilakukan. Kode pseudo dari fungsi pencarian ditunjukkan di bawah ini.
private Result search(Matrix matrix, int remaining) { if (remaining == 0) { return SOLUTION } attempts := attempts + 1 if (attempts >= MAX_ATTEMPTS) { return TIMEOUT } if ( S Z) { S Z if ( ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION } if (result == TIMEOUT) { return TIMEOUT } } } for( , ) { if ( ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION } if (result == TIMEOUT) { return TIMEOUT } } } return NO_SOLUTION }
Matriks asli yang diteruskan ke fungsi pencarian kosong, kecuali untuk baris bawah yang berisi blok 3 kotak yang berdekatan. Ini ditransmisikan bersama dengan jumlah tokoh yang tersisa yang perlu ditambahkan. Jika yang
remaining adalah 0, maka matriks berisi solusi dan fungsi kembali. Setiap panggilan rekursif menambah jumlah upaya
attempts global. Jika melebihi
MAX_ATTEMPTS , yang memiliki nilai 1000, maka pencarian dimulai lagi.
if ketiga mencoba menambahkan tetramino S atau Z ke bagian bawah matriks jika ruang memungkinkan. Arti dari ini adalah untuk menghindari situasi seperti yang ditunjukkan di bawah ini, ketika algoritma menghabiskan waktu mengisi bagian dari matriks, tidak dapat mengisi sisanya karena kurangnya dukungan.
Berkat
if ia dengan cepat membentuk platform untuk membangun:
Untuk mencoba menambahkan angka ke matriks, pemeriksaan di atas diperlukan. Algoritma memeriksa apakah angka tersebut akan memiliki dukungan, mengingat garis yang telah selesai. Ia juga memeriksa untuk melihat apakah ia membagi 4 ukuran setiap ruang kosong yang dibuat oleh penyisipan bentuk.
Konversi gambar
Algoritma Printer Tetris mengubah setiap baris bitmap menjadi serangkaian lintasan. Bergerak dari kiri ke kanan, setiap bagian dengan cara "serakah" memasukkan tetramino J, T dan L ke tempat mereka ditempatkan. Sebagai contoh, gambar di bawah ini menunjukkan deretan 16 bitmap bitmap.
Gambar di bawah ini menunjukkan 5 pass yang diperlukan untuk menutupi 16 piksel ini.
Urutan bentuk yang berusaha dimasukkan oleh algoritma ditentukan oleh warna piksel. Agar bentuk tidak tumpang tindih, digunakan array satu dimensi dari nilai Boolean. Untuk memasukkan angka, 3 elemen nol harus ada dalam array. Setelah berhasil memasukkan gambar 3, elemen array yang sesuai mengambil nilai 1.
Untuk melacak piksel yang diselesaikan antara beberapa lintasan, digunakan array satu dimensi dari nilai Boolean. Ketika setiap item adalah 1, garisnya selesai.
Pada akhir setiap pass, konverter gambar mencari tabel untuk semua pola untuk membuat satu atau lebih kotak. Untuk output, ia melewati pola yang sesuai dengan tetramino J, T dan L. dimasukkan di bagian bawah.Sebagai contoh, pass pertama yang ditunjukkan di atas ditampilkan sebagai pola berikut untuk membuat 5 kotak:
Pencarian waktu nyata
Konverter gambar yang dijelaskan di bagian sebelumnya sangat cepat karena menggunakan tabel konstan yang berisi semua pola untuk membuat kotak, dan tidak mencari mereka secara real time. Namun, pencarian waktu nyata dapat menggunakan pola yang tidak ada dalam tabel, dan oleh karena itu, sangat mengurangi jumlah tetramino yang dibutuhkan untuk menghasilkan gambar. Dia menggunakan kotak yang dibuat di bagian sebelumnya, menggunakannya sebagai dukungan tambahan. Misalnya, seperti yang disebutkan di atas, pola berikut untuk membuat satu kotak membutuhkan 7 garis penuh.
Tapi satu kotak merah yang dibuat di bagian sebelumnya di sudut kiri bawah gambar di bawah ini memberikan dukungan tambahan, mengurangi jumlah garis yang diisi menjadi 3.
Selain itu, pencarian waktu nyata dapat mencakup 3 piksel yang berdekatan dengan warna yang sama dengan membalik tetramino J, T atau L.
Bahkan, ia dapat menggabungkan tetramino terbalik dan terbalik, yang mencakup sejumlah besar piksel dalam satu lintasan. Misalnya, 5 pass di atas yang diperlukan untuk menutupi 16 piksel dapat dikurangi menjadi pass tunggal yang ditunjukkan di bawah.
Untuk mendapatkan pola ini, konverter gambar dimulai dengan mengemas tetramino J, T, dan L. yang terbalik dengan bersemangat
Kemudian dia dengan bersemangat mencoba untuk menambahkan versi yang tidak dilewatinya, dan dalam hal ini dia berhasil menambahkan J.
Pada prinsipnya, tabel pencarian yang dihitung sebelumnya juga dapat digunakan dalam proses ini, tetapi ukuran tipis dari tabel tersebut membuatnya tidak dapat diterapkan dalam praktik.
Dalam contoh ini, 8 kotak dalam satu baris di atas baris yang akan dibuat ditambahkan ke baris bawah dari matriks kosong. Untuk
n kuadrat pada lapangan bermain 21 persegi, ketinggian matriks
h adalah bilangan bulat positif terkecil sehingga
21h - n dapat dibagi 4. Dalam kasus ini, diperlukan matriks dengan ketinggian 4.
Pencarian waktu nyata bekerja dengan cara yang persis sama dengan algoritma pencarian yang dijelaskan di atas, tetapi memiliki sedikit perbaikan. Seperti sebelumnya, tumpukan kolom matriks memberikan dukungan hanya jika tinggi kolom dikurangi jumlah baris yang diselesaikan lebih besar dari nol. Ketika perbedaannya nol, tumpukan kolom seharusnya tidak memberikan dukungan. Namun, dalam versi ini, jika sama dengan nol, ia memeriksa kotak pada baris yang dibuat yang dihasilkan oleh lintasan sebelumnya. Yaitu, setiap kotak di baris di bawah baris bawah matriks memberikan dukungan untuk kolom kosong.
Selain itu, karena pencarian dilakukan secara real time, tidak praktis untuk membuatnya lengkap. Jika dia tidak menemukan solusi setelah sejumlah upaya yang diberikan, maka dia menambahkan 4 baris lagi di bagian atas matriks, dan kemudian mencoba lagi. Setelah itu, jika ia masih tidak dapat menemukan solusi setelah sejumlah upaya yang diberikan, maka dalam bagian ini ia kembali ke metode dengan tabel pencarian yang telah dihitung sebelumnya dan konversi gambar yang dijelaskan pada bagian artikel sebelumnya.
Cetak
Untuk mencetak, Anda harus mengikuti instruksi yang ditampilkan oleh konverter gambar pada bidang Tetris playing. Printer membuat tetramino tertentu di titik tengah atas bidang bermain dalam orientasi standar. Kemudian printer memutarnya, memindahkannya secara horizontal dan menurunkannya. Proses ini ditunjukkan dalam video:
Kode sumber
Kode sumber untuk proyek Java 7 tersedia di
sini .
Algoritme pencarian untuk tabel yang sudah disiapkan dan waktu-nyata ada dalam paket
search.precomputed dan
search.realtime . Mereka menggunakan beberapa kelas umum yang terletak di paket
search . Hasil pencarian pra-perhitungan disimpan dalam paket
patterns sebagai urutan file teks. File teks menyimpan matriks yang dikemas sebagai karakter ASCII, dimulai dengan
A Sebagai contoh, 3 matriks pertama di
emitters1.txt (himpunan pola untuk membuat satu kotak) terlihat seperti ini:
Seperti yang berulang kali dinyatakan dalam artikel, 3 simbol
A berdekatan dalam matriks di atas dapat diganti dengan tetramino J, T atau L. Simbol
B ,
C ,
D dan seterusnya mewakili urutan tetramino yang perlu Anda buat.
Kelas
imageconverter.ImageConverter berisi metode
main , yang menerima argumen baris perintah tunggal: nama file gambar sprite. Suatu gambar tidak boleh lebih besar dari 17 × 32 piksel dan tidak dapat mengandung lebih dari 3 warna buram. Semua piksel lainnya harus transparan.
Menariknya, di video game lama, pengembang sering menggunakan latar belakang untuk mendapatkan warna ekstra. Misalnya, murid dan mulut Gelembung dari Gelembung berbandul, murid Donkey Kong dari Donkey Kong dan alis dengan tahi lalat Nona Pakman dari Ms. Pac-Man sebenarnya transparan. Hitam diperoleh dari latar belakang yang solid.
Latar belakang bidang bermain Tetris dapat digunakan dengan cara yang sama.
Output
ImageConverter terlihat seperti potongan ini:
3 nilai hex pada baris pertama adalah 3 warna buram diekstraksi dari file gambar sprite. Mereka sesuai dengan warna tetramino J, T dan L. Warna tetramino lainnya tidak mempengaruhi gambar. Blok yang tersisa adalah pola paket yang dieksekusi di lapangan bermain (untuk karakter setelah
Z dan hingga
a lihat
tabel karakter ASCII ). Blok kuning yang disorot membentuk platform. Blok pertama menambahkan platform, yang kedua menghapusnya.
Kelas
printer.Printer menerima file teks dalam format ini dan menghasilkan file gambar dengan memainkan Tetris.
Algoritme printer yang digunakan untuk menghasilkan video yang menyerupai
versi Tetes dari
NES menentukan setiap jenis tetramino di setiap blok file teks. Kemudian bergerak dalam urutan yang berlawanan dari titik awal dan orientasi awal ke sudut rotasi dan koordinat penurunan angka yang ditunjukkan dalam file. Catatan: karena kecepatan yang sangat tinggi dari angka yang jatuh, tidak mungkin untuk melampaui level 30 dalam versi SES sebenarnya dari Tetris. Diasumsikan bahwa printer mengirimkan semua perintahnya ke lapangan dengan cukup cepat. untuk mengimbangi ini.
Untuk membuat ulang file pola, gunakan
search.precomputed.PatternSearcher . Itu dapat dikustomisasi dengan mengubah konstanta di awal file kode sumber.
public static final int MATRIX_WIDTH = 21; public static final int MATRIX_HEIGHT = 4; public static final int EMITTED_SQUARES = 4; public static final int RANDOM_SETS = 100000; public static final int MAX_ATTEMPTS = 1000;
RANDOM_SETS adalah jumlah permutasi acak dari 371 cara untuk menambahkan angka ke matriks. Ketika diatur ke
100000 , dibutuhkan beberapa detik untuk menginisialisasi permutasi saat startup. Selain itu, penyimpanan mereka membutuhkan lebih dari satu gigabyte memori.
MAX_ATTEMPTS mengontrol waktu eksekusi pencarian. Nilai
1000 relatif kecil memungkinkan pencarian untuk dengan cepat membuang permulaan acak yang gagal menunjukkan diri dengan baik. Namun, untuk membuktikan bahwa untuk ukuran matriks spesifik dan jumlah kotak yang dibuat tidak ada solusi, perlu untuk mengeksplorasi seluruh ruang pencarian secara penuh. Untuk melakukan ini, Anda dapat mengatur
MAX_ATTEMPTS ke
Integer.MAX_VALUE .
Konstanta serupa ditemukan di
search.realtime.RealtimeSearcher , yang digunakan oleh konverter gambar. Seperti disebutkan di atas, nilai
RANDOM_SETS besar membutuhkan peningkatan memori maksimum dan mengarah ke awal yang lebih lama.
MAX_RETRIES mengontrol jumlah upaya, setelah itu pencarian real-time menyerah dan kembali ke pencarian dengan tabel yang sudah dihitung sebelumnya.
Perlu diingat bahwa kedua algoritma pencarian menggunakan 100% CPU, menciptakan banyak utas paralel yang ukurannya sama dengan jumlah prosesor yang tersedia.