Halo, Habr! Saya mempersembahkan kepada Anda terjemahan artikel
"Penjelasan intuitif tentang Pengujian Hipotesis dan Nilai-P" oleh Joos Korstanje.
Beberapa tahun yang lalu, saya melakukan pekerjaan statistik freelance pertama saya untuk perusahaan pengiriman buah dan sayuran. Dua puluh empat jam sehari, produk yang masuk dari petani, sebelum dikirim ke supermarket, melewati departemen kontrol kualitas. Pilihan produk dilakukan secara acak oleh karyawan departemen ini.
Dalam laporan tahunan, mereka memperhatikan bahwa kualitas tahun ini lebih rendah daripada kualitas di masa lalu: perbedaannya sekitar setengah poin pada skala 1 hingga 10.
Lalu mereka mengundang saya. Saya harus menjawab pertanyaan:
Apakah 0,5 poin ini perbedaan yang signifikan?Jika Anda tidak tahu statistiknya, maka pertanyaan ini mungkin aneh bagi Anda. Tapi jangan khawatir: tujuan artikel ini adalah untuk menunjukkan kepada Anda bagaimana Anda dapat menjawab pertanyaan ini menggunakan pengujian hipotesis, juga disebut inferensi statistik.
Permainan angka: kontribusi satu apel
Bayangkan Anda memeriksa apel baik atau buruk, menggunakan apel pilihan acak dari kotak yang sangat besar dengan apel. Pada gambar di bawah ini kita melihat efek nyata dari ukuran sampel pada pengukuran: efek satu apel sangat signifikan untuk sampel kecil dan menjadi kurang dan kurang signifikan, semakin besar ukuran sampel.
Kontribusi satu apel tergantung pada ukuran sampel.Memahami pengaruh ukuran sampel adalah dasar pertama untuk memahami pengujian hipotesis. Kita dapat mulai berpendapat bahwa 0,5 pada 2 apel akan seperti perbedaan 1 apel, sangat kecil. Tetapi untuk 100 apel, 0,5 akan menjadi perbedaan 50 apel: perbedaan yang sangat besar!
Untuk sampel kecil, 0,5 poin adalah perbedaan kecil, tetapi untuk sampel besar 0,5, ini adalah perbedaan besar.Seberapa besar sampel seharusnya: pengujian hipotesis dan signifikansi sebagai jawaban
Ada beberapa cara untuk menjawab pertanyaan ini, tetapi dalam artikel ini saya akan terjun ke inferensi statistik atau pengujian hipotesis.
Pengujian hipotesis adalah kumpulan metode statistik yang digunakan untuk memahami bagaimana pengambilan sampel objek yang diamati dapat digunakan untuk menerima atau menolak hipotesis yang telah ditentukan. Pengujian hipotesis digunakan untuk menyelesaikan banyak masalah, terutama dalam penelitian ilmiah dan sebagai metode utama dalam pemasaran online (pengujian A \ B).
Matematikawan telah mengembangkan tes hipotesis sedemikian rupa sehingga ada prosedur tertentu untuk menemukan kebenaran.
Pengujian hipotesis memungkinkan Anda hanya menguji hipotesis, tetapi tidak untuk mengembangkannya.Dari kotak di mana 100 apel (sebut saja populasi), kami mengambil sampel 8 apel. Tahun ini, dari 8 apel, 5 busuk (62%), dan dalam sampel tahun lalu, dari 8 apel, hanya 4 yang busuk (50%). Kami ingin menggunakan uji hipotesis untuk menentukan apakah persentase apel busuk tahun ini lebih besar dari tahun lalu.
Pengujian hipotesis adalah alternatif matematis untuk mengukur populasi. Berkat perhitungan ini, kami dapat menggeneralisasi pengukuran sampel kecil ke populasi besar. Jadi kami melakukan lebih sedikit pekerjaan.
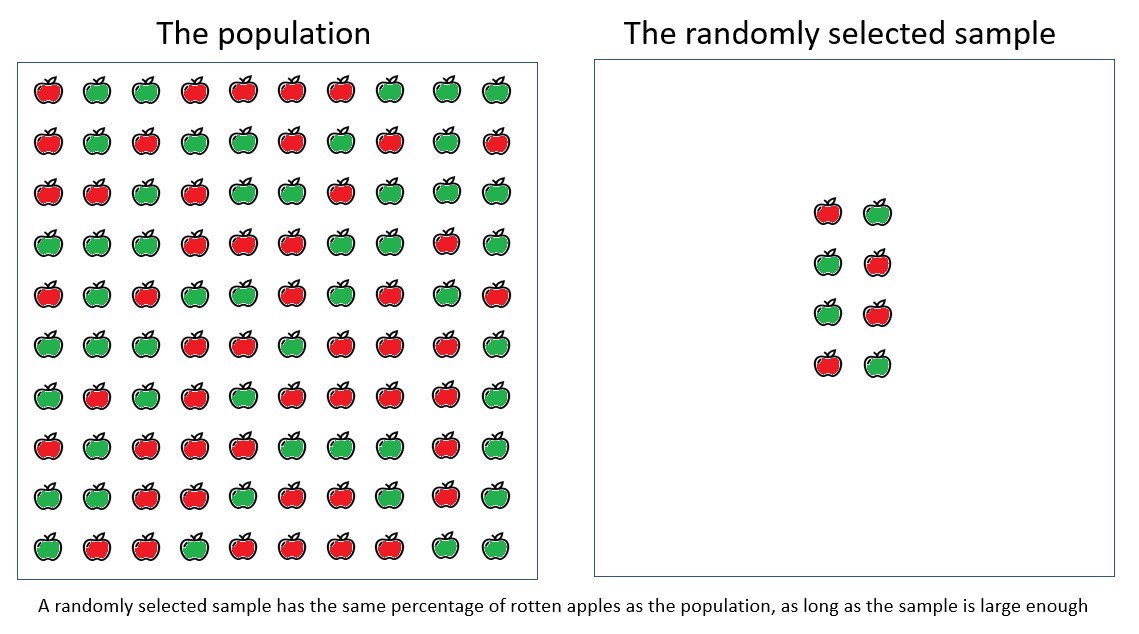
Sampel sampel acak memiliki persentase apel busuk yang sama dengan populasi umum, asalkan sampel sampel cukup besar.
Matematikawan telah menemukan cara untuk menggeneralisasi kesimpulan berdasarkan sampel kepada populasi umum.
Metode ini dimulai dengan rumusan hipotesis penelitian yang jelas. Sayangnya, matematika hanya berfungsi jika kita sudah memiliki gagasan tentang apa yang ingin kita uji.
Hipotesis utama untuk contoh kita:
Persentase apel busuk dalam populasi umum tahun ini lebih dari di masa lalu.Tes hipotesis aktual
Matematika pengujian hipotesis membentuk keseimbangan antara hasil pengukuran sampel dengan jumlah pengamatan. Hasilnya adalah nilai p.Perhitungan ini melalui penggunaan distribusi: untuk hampir setiap situasi imajiner, hukum matematika telah diturunkan yang menggambarkan hasil yang diharapkan.
Untuk pertanyaan ya / tidak, seperti pertanyaan tentang apel busuk kami (busuk / tidak busuk), hukum lemparan koin berlaku. Ini adalah contoh paling sederhana dari hukum matematika: 50% ekor, 50% elang.
Ini juga dapat dengan sederhana direpresentasikan sebagai distribusi matematika standar yang memberi tahu kita tentang probabilitas pengamatan. Misalnya, 7 elang keluar dari 10 koin terbalik. Ini disebut distribusi binomial dan dapat direpresentasikan sebagai berikut:
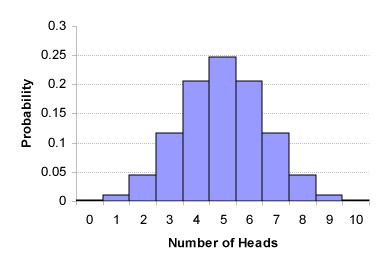distribusi binomial dari 10 flips koin.Dalam artikel ini saya akan jauh dari matematika keras, tetapi penting untuk mengetahui bahwa kita dapat menggunakan rumus matematika untuk mengevaluasi apakah persentase yang diamati jauh dari persentase yang diharapkan.
Pada akhir artikel ini saya akan memberi Anda daftar formula pengujian hipotesis yang umum digunakan untuk berbagai kasus, dan setelah itu saya akan menjelaskan cara menggunakannya. Tetapi pertama-tama, saya akan menjelaskan interpretasi pengujian hipotesis.
Hasil Uji Hipotesis: p-value
Di belakang pengujian hipotesis ada keseimbangan matematis antara nilai yang diamati dan ukuran sampel. Pada akhir perhitungan, setiap opsi pengujian hipotesis yang ada akan menghasilkan skor terstandarisasi yang akan memungkinkan Anda untuk membandingkan hasilnya bahkan ketika matematika tidak persis sama.
Nilai-P adalah cara standar untuk merumuskan hasil tes hipotesis dan menggunakannya dalam tes lain.
Nilai-P adalah angka antara 0 dan 1 yang memberi tahu kita jika perbedaannya antara pengamatan sampel dan hipotesis kita sangat berbeda. Nilai referensi adalah 0,05.
Perbedaannya signifikan secara statistik jika p-value kurang dari 0,05.
Dan perbedaannya tidak signifikan secara statistik jika p-value lebih besar dari 0,05.
Contoh 1:
Kami membuat 10 koin terbalik.
Hipotesis kami: kami mengharapkan 5 ekor.
Pengamatan kami: kami mendapat 6 ekor.
Perhitungan p-value menghasilkan 0,518, yang lebih dari 0,05.
Kesimpulan kami: perbedaannya tidak signifikan secara statistik.
Interpretasi kami: hasilnya konsisten dengan hipotesis.
Contoh 2:
Kami membuat 10 koin terbalik
Hipotesis kami: kami mengharapkan 5 ekor.
Hasil kami: kami mendapat 10 ekor.
Nilai p kami adalah 0,0, yang kurang dari 0,05.
Kesimpulan kami: perbedaannya signifikan secara statistik
Interpretasi kami: hasilnya tidak konsisten dengan hipotesis.
Contoh 3:
Kami memeriksa 10 apel.
Hipotesis kami: kami mengharapkan 1 apel busuk.
Hasil kami: kami mendapat 1 apel busuk.
Nilai p kami adalah 1,0 yang lebih dari 0,05.
Kesimpulan kami: perbedaannya tidak signifikan secara statistik
Interpretasi kami: hasilnya konsisten dengan hipotesis.
Contoh 4:
Kami memeriksa 10 apel.
Hipotesis kami: kami mengharapkan 1 apel busuk.
Hasil kami: kami mendapat 5 apel busuk.
Nilai p kami adalah 0,0114 yang kurang dari 0,05.
Kesimpulan kami: perbedaannya signifikan secara statistik
Interpretasi kami: hasilnya tidak konsisten dengan hipotesis.
Kesimpulan
Dalam artikel ini, saya memberikan interpretasi intuitif tentang struktur umum kesalahan statistik atau pengujian hipotesis. Saya harap sekarang Anda lebih memahami pengujian hipotesis, dan bagaimana ini dapat bermanfaat bagi Anda.
Saya tidak masuk jauh ke dalam bukti matematika dan ke rincian spesifik. Tabel di bawah ini memberikan daftar tes hipotesis paling sering yang saya rekomendasikan untuk studi lebih lanjut.
Daftar dengan hipotesis alternatif untuk beberapa tes hipotesis.
Saya harap artikel ini bermanfaat bagi Anda, dan semoga Anda beruntung dalam penelitian lebih lanjut tentang pengujian hipotesis.