Hipotesis utama kembar adalah salah satu masalah yang paling penting dan kompleks dalam matematika. Dua ahli matematika menyelesaikan versi paralel dari masalah ini untuk sistem numerik kecil.

Pada tanggal 7 September, dua ahli matematika
menerbitkan bukti versi salah satu masalah terbuka paling terkenal dalam matematika. Hasilnya membuka front baru dalam studi hipotesis
bilangan prima kembar yang telah mengganggu matematikawan selama lebih dari seratus tahun dan dikaitkan dengan beberapa sifat aritmatika yang paling mendalam.
"Kami telah tergelincir untuk waktu yang lama dan kami kehabisan ide untuk tugas ini, jadi itu adalah kesenangan alami bagi seseorang untuk memiliki ide-ide baru," kata
James Maynard , seorang ahli matematika dari Oxford.
Hipotesis utama kembar berlaku untuk pasangan bilangan prima yang berbeda dengan 2. Si kembar adalah angka 5 dan 7. Dan 17 dan 19. Hipotesis menyatakan bahwa ada jumlah tak terbatas dari pasangan tersebut di antara bilangan alami. Selama dekade terakhir, ahli matematika telah membuat kemajuan yang signifikan, tetapi mereka masih sangat jauh dari solusi lengkap untuk masalah tersebut.
Para penulis bukti baru,
Will Savin dari Columbia University dan
Mark Shusterman dari University of Wisconsin di Madison, membuktikan hipotesis untuk dunia matematika yang lebih kecil, tetapi masih nyata. Mereka membuktikan validitasnya dalam kasus sistem numerik terbatas di mana hanya ada beberapa angka.
Sistem angka seperti itu disebut "bidang terbatas". Meskipun ukurannya kecil, mereka mempertahankan banyak properti matematika yang melekat dalam bilangan bulat yang tak terhitung jumlahnya. Matematikawan berusaha menemukan jawaban untuk pertanyaan aritmatika di bidang terbatas, dan berharap untuk menerjemahkan hasil ini ke semua bilangan bulat.
"Mimpi terakhir, meskipun agak naif, adalah bahwa pemahaman yang baik tentang sifat-sifat bidang yang terbatas dapat menjelaskan dunia bilangan bulat," kata Maynard.
Selain membuktikan hipotesis bilangan prima kembar, Savin dan Shusterman menemukan hasil yang bahkan lebih mengejutkan mengenai perilaku bilangan prima dalam sistem numerik kecil. Mereka membuktikan frekuensi yang tepat dengan mana kembar prima muncul pada interval kecil - dan hasil ini memungkinkan untuk mengendalikan fenomena yang sangat tepat seperti prima kembar. Matematikawan bermimpi mencapai hasil yang sama dengan angka biasa; mereka mengeksplorasi bukti baru dalam mencari ide yang berlaku untuk bilangan prima pada garis angka.
Jenis perdana baru
Prediksi yang paling terkenal dari hipotesis prime kembar adalah adanya sejumlah besar pasangan angka yang berbeda dengan 2. Namun, pernyataan ini lebih umum. Dikatakan bahwa ada jumlah bilangan prima tak terbatas yang berbeda dengan 4 (misalnya, 3 dan 7), atau 14 (293 dan 307), atau dengan nomor apa pun yang Anda tentukan.
Alfons de Polignac
membuat asumsi ini dalam bentuk modern pada tahun 1849. Selama 160 tahun berikutnya, ahli matematika tidak banyak maju dengannya. Namun, pada 2013, es pecah, atau setidaknya retak serius. Tahun itu,
Zhang Ethan membuktikan keberadaan sejumlah besar pasangan bilangan prima, berbeda tidak lebih dari 70 juta.Tahun berikutnya, matematikawan lain, termasuk Maynard dan
Terry Tao , secara serius mengurangi kesenjangan ini. Catatan saat ini adalah bukti keberadaan sejumlah besar bilangan prima yang berbeda satu sama lain dengan tidak lebih dari 246.
Namun, setelah itu, progresnya surut. Matematikawan memahami perlunya ide yang sama sekali baru untuk sepenuhnya menyelesaikan masalah ini. Dan sistem angka hingga adalah tempat yang bagus untuk mencari ide ini.
Untuk membangun bidang terbatas, Anda harus terlebih dahulu mengekstrak subset angka hingga dari angka natural. Anda dapat, misalnya, mengambil lima angka pertama (atau nomor utama apa saja). Dan alih-alih mewakili angka pada garis angka, seperti biasa, bayangkan sistem angka baru dalam bentuk dial.
Aritmatika, seperti yang Anda duga, mulai bekerja di ruang terbatas. Apa yang akan menjadi 4 + 3 dalam sistem numerik terbatas yang terdiri dari lima elemen? Kita mulai dengan 4, hitung tiga divisi searah jarum jam, dan sampai pada 2. Pengurangan, perkalian dan pembagian bekerja dengan cara yang sama.

Tapi hanya ada yang menangkap. Dalam bidang yang terbatas, definisi prime yang biasa tidak masuk akal. Di bidang terakhir, angka apa pun dibagi dengan yang lain. Misalnya, 7 biasanya tidak habis dibagi 3. Tetapi pada bidang terakhir dari lima elemen, itu dapat dibagi. Itu karena pada bidang terakhir ini angka 7 sama dengan angka 12 - keduanya berakhir pada 2 tanda dial. Oleh karena itu, 7 dibagi 3 akan memberikan sama dengan 12 dibagi 3 - dan 12 dibagi 3 akan memberi 4.
Oleh karena itu, hipotesis bilangan prima kembar untuk bidang terbatas mengacu pada polinomial sederhana - ekspresi matematis seperti, misalnya, x
2 +1.
Misalkan, misalnya, bahwa bidang terakhir Anda berisi angka 1, 2, dan 3. Angka-angka ini akan menjadi koefisien polinomial dalam bidang terbatas ini, dan polinomial "sederhana" akan menjadi salah satu yang tidak dapat diuraikan menjadi faktor polinomial. Oleh karena itu, x
2 + x + 2 akan sederhana, karena tidak dapat difaktorkan, tetapi x
2 - 1 tidak akan: ini adalah produk dari (x + 1) dan (x - 1).
Setelah mendefinisikan polinomial sederhana, adalah wajar untuk mengajukan pertanyaan tentang polinomial kembar sederhana - pasangan polinomial yang sederhana dan berbeda dengan nilai tetap. Misalnya, polinomial x
2 + x + 2 sederhana, seperti x
2 + 2x + 2. Mereka berbeda dengan x.
Hipotesa polinomial kembar sederhana untuk bidang berhingga menunjukkan keberadaan pasangan polinomial kembar sederhana yang jumlahnya sangat jauh berbeda, tidak hanya dengan x, tetapi dengan nilai apa pun.
Potongan rapi
Konsep bidang terbatas dan polinomial sederhana mungkin kelihatan tidak masuk akal, dan tidak berguna untuk mempelajari sifat-sifat angka. Tapi mereka tampak seperti simulator badai - alam semesta itu sendiri, memberikan ide tentang fenomena yang terjadi di dunia besar.
"Ada analogi kuno antara bilangan bulat dan polinomial, yang memungkinkan kita untuk mengubah masalah yang berpotensi sangat kompleks terkait dengan bilangan bulat menjadi masalah yang terkait dengan polinomial, yang juga berpotensi kompleks, tetapi mungkin lebih mudah untuk dipecahkan," kata Shusterman.
Bidang terbatas menjadi terkenal pada tahun 1940 ketika
Andre Weil mengembangkan cara yang tepat untuk menerjemahkan aritmatika sistem bilangan kecil menjadi aritmatika bilangan bulat. Weil menggunakan koneksi ini dengan hasil yang luar biasa. Dia
membuktikan , mungkin, masalah paling penting dalam matematika - hipotesis Riemann - untuk kasus dengan seperangkat kurva di atas bidang yang terbatas (masalah ini dikenal dengan nama hipotesis geometri Riemann). Bukti ini, bersama dengan seperangkat
hipotesis Weyl tambahan
, menjadikan bidang terbatas sebagai lanskap kaya untuk penemuan matematika.
Gagasan utama Weil adalah bahwa dalam bidang terbatas, teknik geometris dapat digunakan untuk menemukan jawaban atas pertanyaan tentang angka. “Ini adalah fitur bidang terbatas. Banyak tugas yang ingin Anda selesaikan dapat diulang secara geometris, ”kata Shusterman.
Untuk memahami bagaimana geometri muncul dalam lingkungan seperti itu, bayangkan setiap polinomial sebagai titik dalam ruang. Koefisien polinom berfungsi sebagai koordinat yang menentukan lokasinya. Kembali ke bidang terakhir kami dari 1, 2, dan 3, polinomial 2x + 3 terletak di titik (2, 3) dari ruang dua dimensi.
Tetapi bahkan dalam ruang terbatas yang paling sederhana pun ada banyak polinomial. Polinomial yang lebih kompleks dapat dibuat dengan meningkatkan eksponen dari eksponen terbesar, atau tingkat ekspresi. Dalam kasus kami, polinomial x
2 - 3x - 1 akan diwakili oleh titik dalam ruang tiga dimensi. Dan polinomial 3x
7 + 2x
6 + 2x
5 - 2x
4 - 3x
3 + x
2 - 2x + 3 akan diwakili oleh sebuah titik dalam ruang delapan dimensi.
Dalam karya baru, ruang geometris ini mewakili semua polinomial dengan derajat tertentu untuk bidang terbatas yang diberikan. Pertanyaannya berubah menjadi sebagai berikut: apakah ada cara untuk mengisolasi semua poin yang menunjukkan polinomial sederhana?
Strategi Savin dan Shusterman adalah membagi ruang menjadi dua bagian. Di satu bagian akan ada semua titik yang sesuai dengan polinomial dengan sejumlah faktor genap. Di sisi lain, semua titik berhubungan dengan polinomial dengan jumlah faktor ganjil.
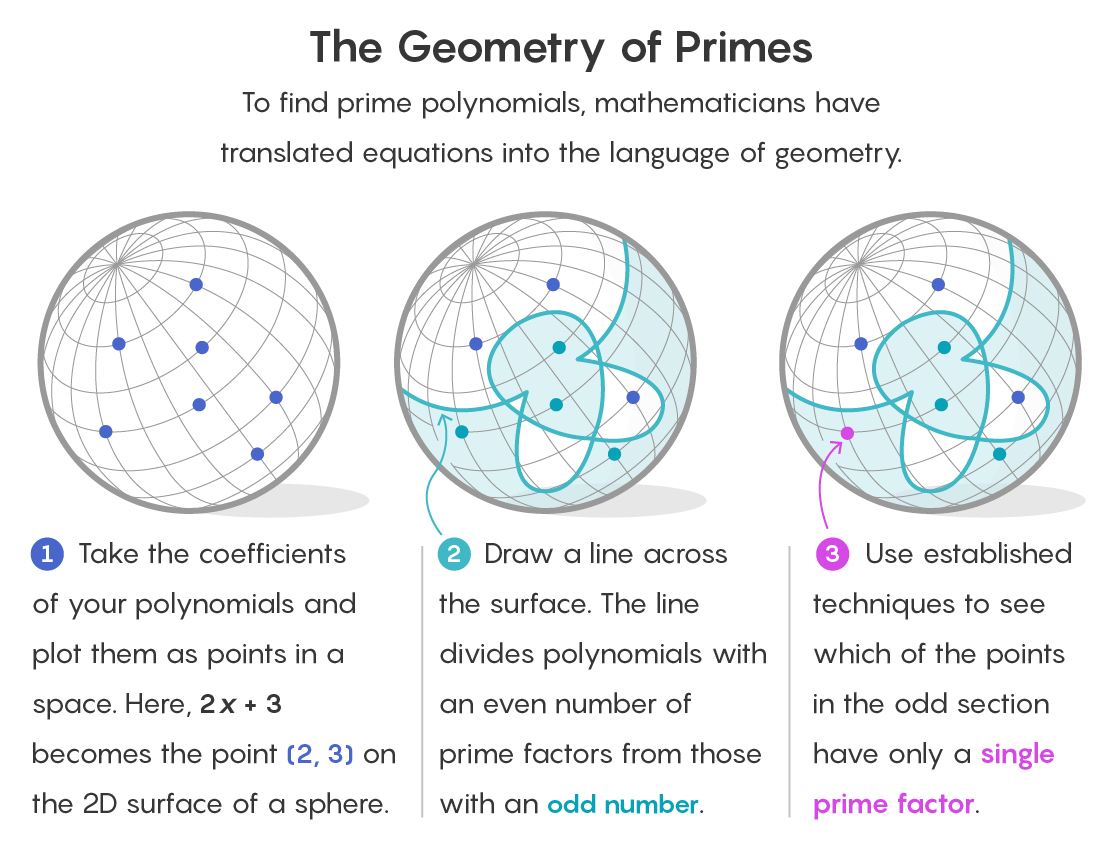
Ini sudah menyederhanakan tugas. Hipotesis polinomial kembar sederhana untuk bidang berhingga hanya berlaku untuk polinomial dengan satu faktor (seperti halnya prima memiliki satu faktor, itu sendiri). Dan karena angka 1 ganjil, bagian dari ruang yang mengandung polinomial dengan sejumlah faktor genap dapat segera dibuang.
Caranya adalah dengan menggunakan pembagian. Dalam kasus objek dua dimensi, misalnya, permukaan bola, ia dipotong setengah oleh kurva satu dimensi - sama seperti khatulistiwa memotong permukaan bumi. Objek dengan jumlah besar dimensi selalu dapat dipotong dengan objek dengan jumlah dimensi lebih sedikit satu.
Tetapi bentuk-bentuk ini dengan dimensi yang lebih sedikit, yang membagi ruang polinomial, sama sekali tidak seindah khatulistiwa. Mereka digambar sesuai dengan rumus matematika yang disebut
fungsi Mobius . Pada input, dibutuhkan polinomial, dan pada output memberikan 1 jika polinomial memiliki bilangan genap faktor prima, -1 jika memiliki bilangan ganjil, dan 0 jika faktorisasi (karena 16 dapat dibagi 2 × 2 × 2 × 2).
Kurva yang digambar oleh fungsi Mobius menekuk dan berputar seperti orang gila, berpotongan dengan diri mereka sendiri di banyak tempat. Tempat-tempat ini, yang disebut singularitas, sangat sulit untuk dianalisis (mereka sesuai dengan polinomial yang dapat didekomposisi menjadi beberapa faktor utama yang identik).
Inovasi mendasar dari Savin dan Shusterman adalah bahwa mereka menemukan cara yang tepat untuk memotong loop dengan pengukuran lebih sedikit menjadi segmen yang lebih pendek. Segmen ini lebih mudah dipelajari daripada keseluruhan loop.
Setelah menyusun katalog polinomial dengan jumlah faktor prima yang ganjil - dan ini yang paling sulit - Savin dan Shusterman dihadapkan pada tugas menentukan mana yang sederhana dan mana yang kembar. Untuk melakukan ini, mereka menerapkan beberapa formula yang digunakan oleh ahli matematika untuk mempelajari bilangan prima di antara yang biasa.
Savin dan Shusterman menggunakan teknik mereka untuk membuktikan dua poin penting tentang polinomial sederhana di bidang terbatas tertentu.
Pertama, hipotesis bilangan prima kembar dalam bidang hingga benar: ada banyak pasangan polinomial kembar yang berbeda dengan nilai yang diberikan.
Kedua, dan yang lebih penting, karya ini menyediakan penghitungan akurat jumlah polinomial kembar sederhana yang dapat ditemukan di antara polinomial dengan urutan tertentu. Ini analog dengan mengetahui berapa banyak bilangan prima kembar yang berada di dalam interval yang cukup panjang pada garis bilangan - dan ini hanyalah impian para ahli matematika.
"Ini adalah karya pertama yang memberikan analogi kuantitatif tentang apa yang seharusnya benar untuk bilangan bulat, dan ini adalah hasil yang sangat luar biasa," kata Ziv Rudnik dari Universitas Tel Aviv. "Sejauh ini, tidak ada yang seperti ini yang terjadi."
Bukti dari Savin dan Schusterman menunjukkan bagaimana, hampir 80 tahun setelah Andre Weil membuktikan hipotesis Riemann untuk kurva di bidang terbatas, matematikawan masih dengan keras kepala bergerak ke arah ini. Sekarang, ahli matematika yang berurusan dengan hipotesis utama kembar akan beralih ke karya Savin dan Shusterman, dan mungkin itu akan memberi mereka sumber inspirasi yang mendalam.