👩🏻‍💻 👏🏻 👇 Apa anggota selanjutnya ...? - Kami mencari rumus untuk istilah ke-n dari urutan, menghasilkan fungsi dan transformasi-Z 👩🏻‍🚀 ❗️ 👬

Anda dapat mengunduh file dengan kode dan data di posting asli di blog saya

Bahasa Wolfram memiliki empat fitur yang benar-benar luar biasa: FindSequenceFunction , RSolve , DifferenceRootReduce dan FindFormula . Pada artikel ini, kita membahas kemampuan mereka dan berbicara tentang fungsi yang berkaitan erat dengan mereka - untuk mencari parameter rekursi linear FindLinearRecurrence (koefisien dari persamaan perulangan linear), menghasilkan fungsi GeneratingFunction dan ZTransform .

Fungsi pertama , FindSequenceFunction, mencari ekspresi untuk anggota ke-nnya dengan urutan angka tanpa memerlukan apa-apa lagi.

 Hold @ FindSequenceFunction[{1, 1, 2, 3, 5, 8, 13}, n]

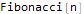
 FindSequenceFunction[ {-2, 4Sqrt[Pi], -16, 16Sqrt[Pi], -128/3, 32Sqrt[Pi], -1024/15, 128Sqrt[Pi]/3, -8192/105, 128Sqrt[Pi]/3}, n]

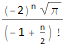Fungsi kedua , RSolve, memecahkan persamaan perulangan dari berbagai jenis. Elemen mungkin terlihat seperti

a [f [n]]

$a [f [n]]$ ,

a [f [f [n]]]

$a [f [f [n]]]$ ,

a [f [f [t e x t . . . f [n] t e x t . . .]]]

$a [f [f [\ text {...} f [n] \ text {...}]]]$ , di mana f memiliki bentuk: n + A (persamaan perbedaan aritmatika), B * n - persamaan geometrik atau perbedaan q), B * n + a (persamaan perbedaan fungsional aritmatika-geometris), B * n ^ d (fungsi geometri daya persamaan perbedaan), (A * n + B) / (C * n + D) (persamaan perbedaan fungsional fraksional linear).

 RSolve[ { a[n + 3]==2 * a[n], a[1]==α, a[2]==β, a[3]==γ }, a, n ]

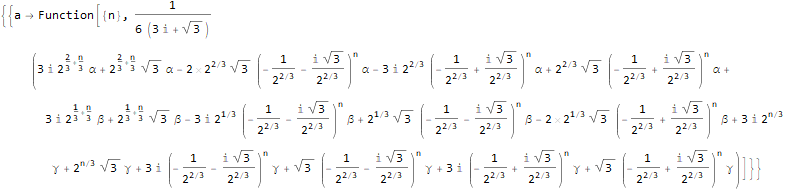
 RSolve[ { v[n]==(2 * Pi * v[n - 2]) / n, v[2]==Pi, v[3]==(4 * Pi) / 3 }, v @ n, n ]

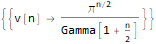Fungsi ketiga - DifferenceRootReduce - mencari hubungan perulangan untuk urutan angka, anggota ke-n yang memiliki bentuk tertentu.

 DifferenceRootReduce[-2 * n * Pi * Factorial[(n * 2) - 1], n ]

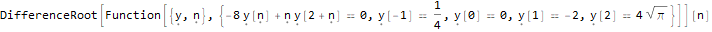
 RSolve[ { (-8 * y[n]) + n * y[2 + n]==0, y[-1]==1/4, y[0]==0, y[1]==-2, y[2]==4Sqrt[Pi] }, y, n ]

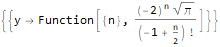
Fungsi ini dapat melakukan lebih banyak lagi, katakanlah, memverifikasi identitas berkenaan dengan urutan, misalnya:

 DifferenceRootReduce[Fibonacci[2 * n]==Fibonacci[n] * LucasL[n], n]

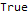
Di sini LucasL adalah urutan angka Luc (ini, pada kenyataannya, urutan Fibonacci, hanya anggota pertama yang tidak 1, 1, tetapi 1, 3.

 Hold @ DifferenceRootReduce @ LucasL @ n

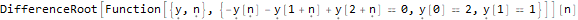
 DifferenceRootReduce[LucasL[n]==Fibonacci[n - 1] + Fibonacci[n + 1]]

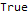
Bagaimana menemukan formula perulangan untuk suatu urutan?

Metode pencarian untuk anggota umum dari urutan sering didasarkan pada kebutuhan untuk memilih persamaan perulangan.

Ini bisa bekerja seperti ini: mari kita mencari anggota urutan ke-n dalam formulir

f [n] = s u m_{i = 1}^{k} a [i] f [n - i]

$f [n] = \ sum_ {i = 1} ^ ka [i] f [n-i]$ . Mari kita memiliki anggota urutan pertama:

 sequence = {1, 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461}

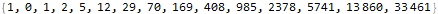
Mari kita coba menemukan ekspresi untuk istilah ke-n dalam formulir

f [n] = s u m_{i = 1}^{1} a [i] f [n - i] = a [1] f [n - 1]

$f [n] = \ sum_ {i = 1} ^ 1a [i] f [n-i] = a [1] f [n-1]$ :

 seauenseEq1 = MovingMap[ Function[ Dot[Part[#, 1;;1], {a @ 1}]==Part[#, -1] ], sequence, 1 ]

 Hold @ Solve @ seauenseEq1

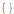
Seperti yang Anda lihat, tidak ada solusi.

Ayo coba cari sekarang di form

f [n] = s u m_{i = 1}^{2} a [i] f [n - i] = a [1] f [n - 1] + a [2] f [n - 2]

$f [n] = \ sum_ {i = 1} ^ 2a [i] f [n-i] = a [1] f [n-1] + a [2] f [n-2]$ :

 seauenseEq2 = MovingMap[ Function[ Dot[Part[#, 1;;2], {a @ 1, a @ 2}]==Part[#, -1] ], sequence, 2 ]

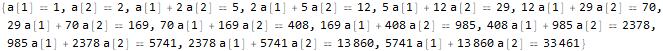
 Hold @ Solve @ seauenseEq2

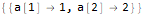
Seperti yang kita lihat, ternyata. Oleh karena itu, istilah ke-9 berbentuk:

f [n] = f [n - 1] + 2 f [n - 2]

$f [n] = f [n-1] + 2f [n-2]$ .

Sebenarnya ada fungsi FindLinearRecurrence yang memungkinkan Anda menemukan rekursi linier, mirip dengan bagaimana kami baru saja melakukannya:

 Hold @ FindLinearRecurrence @ sequence

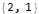
Menggunakan fungsi LinearRecurrence , LinearRecurrence dapat memperluas urutan:

 LinearRecurrence[{2, 1}, sequence[[1;;2]], 50]

Atau gabungkan semuanya menjadi satu baris dengan membangun fungsi yang: memperluas urutan, menghasilkan persamaan perbedaan dan menemukan rumus umum untuk istilah ke-n:

 sequenseExtension[list_, n_] := Module[ {lr, eq}, lr = FindLinearRecurrence @ list; eq = Flatten[ { a[k]==Total[ Table[ a[k + -i] * Part[lr, i], {i, 1, Length @ lr} ] ], Table[a[i], list[[i]]], {i, 1, Length @ lr}] } ]; <| "" -> eq, "" -> FullSimplify[a[k] /. Part[RSolve[eq, a, k], 1]], "" -> LinearRecurrence[lr, Part[list, Span[1, Length[lr]]], n] |> ];

 Hold @ sequenseExtension[{1, 1, 2, 3, 5}, 20]

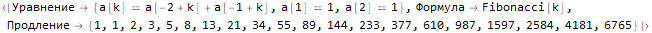
 Hold @ sequenseExtension[{1, 2, 2, 1, 1, 2, 2, 1}, 20]

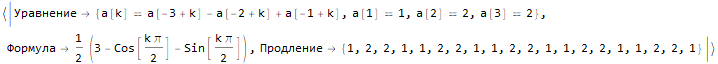
 Hold @ sequenseExtension[ {1, 0, -1, 0, 2, 0, -2, 0, 3, 0, -3, 0, 4, 0, -4}, 25 ]

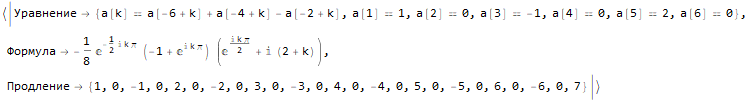
Bagaimana menemukan formula untuk anggota urutan ke-n?

Konversi z

Transformasi-Z terdiri dalam menghitung serangkaian bentuk

s u m_{n = 0}^{i n f t y} f (n) z^{- n}

$\ sum_ {n = 0} ^ {\ infty} f (n) z ^ {- n}$ dari fungsi diskrit

f (n)

$f (n)$ . Transformasi ini memungkinkan kita untuk mengurangi persamaan perulangan untuk mengatur urutan ke persamaan untuk gambar fungsi

f (n)

$f (n)$ , yang mirip dengan transformasi Laplace, yang mengurangi persamaan diferensial ke persamaan aljabar.

Begini cara kerjanya:

 Grid[ Transpose[ Function[ { #, Map[TraditionalForm, Map[FullSimplify, ZTransform[#, n, z]]] } ][ { f[n - 2], f[n - 1], f @ n, f[n + 1], f[n + 2] } ] ], Background -> White, Dividers -> All ]

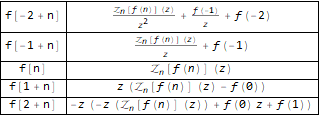
Mari kita lihat contoh, katakanlah, ambil urutan Fibonacci yang terkenal:

 fibonacciEq = f[n]==f[n - 1] + f[n - 2]; initialConditions = {f[1] -> 1, f[2] -> 1};

Jelas bahwa itu harus ditulis ulang dalam bentuk, seperti yang ditunjukkan di bawah ini, sehingga konstruksi suka

f (- 1)

$f (-1)$ setelah menerapkan Z-transform.

 fibonacciEq = f[n + 2]==f[n + 1] + f[n]; initialConditions = {f[0] -> 1, f[1] -> 1};

Kami melakukan transformasi-Z:

 fibonacciEqZTransformed = ReplaceAll[fibonacciEq, pattern:f[__] :> ZTransform[pattern, n, z]]

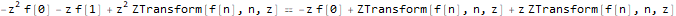
Kami memecahkan persamaan untuk gambar fungsi f - ZTransformasi [f [n], n, z]:

 fZTransformed = ReplaceAll[ ZTransform[f @ n, n, z], Part[Solve[fibonacciEqZTransformed, ZTransform[f @ n, n, z]], 1] ]

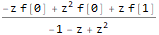
Kami melakukan transformasi Z terbalik, menggantikan kondisi awal pada saat yang sama (kami mengganti n dengan n-1 dalam ekspresi akhir sehingga urutan kami memiliki pengindeksan yang benar (dari yang pertama, bukan istilah nol):

 ReplaceAll[InverseZTransform[fZTransformed /. initialConditions, z, n], n -> (n - 1) ]

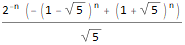
Secara alami, ini dapat diotomatisasi dengan membuat rekanan RSolve Anda sendiri:

 myRSolve[eq_, initials_, f_, n_] := Module[ {z, initialsInner, eqZTransformed, fZTransformed}, initialsInner = ReplaceAll[initials, f[x_] :> f[x - 1]]; eqZTransformed = ReplaceAll[eq, pattern:f[__] :> ZTransform[pattern, n, z]]; fZTransformed = ReplaceAll[ZTransform[f @ n, n, z], Part[Solve[eqZTransformed, ZTransform[f @ n, n, z]], 1] ]; FullSimplify[ InverseZTransform[fZTransformed /. initialsInner, z, n] /. n -> (n - 1) ] ];

 myRSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]) }, {f[1] -> 20, f[2] -> 0}, f, n ]

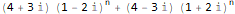
 RSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]), f[1]==20, f[2]==0 }, f, n ]

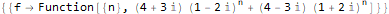
Tapi, tentu saja, RSolve mengandung lebih banyak kemungkinan untuk menyelesaikan berbagai persamaan diskrit, yang tidak akan kita bahas lebih rinci:

 RSolve[a[n]==(n * a[n]) + n, a, n], RSolve[ { a[n + 1]==(2 * a[n]) + (3 * a[n]) + 4, a[0]==0 }, a, n ], RSolve[ y[n + 1 * 3]==(2 * y[n + 1 * 6]) + n * 2, y, n ]

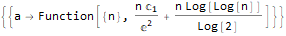
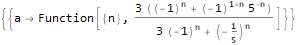
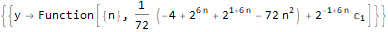
Menghasilkan fungsi

Menghasilkan fungsi urutan

a (n)

$a (n)$ ini adalah fungsi seperti itu

G (x)

$G (x)$ , perluasan yang dalam seri Taylor (atau, lebih luas, Laurent) memiliki bentuk -

G (x) = s u m_{i = 0}^{i n f t y} a (n) x^{n}

$G (x) = \ sum_ {i = 0} ^ {\ infty} a (n) x ^ n$ . Dengan kata lain, koefisien kekuatan x dalam perluasan fungsi dalam suatu rangkaian menentukan urutan kita.

Katakan fungsi

G (x) = f r a c 1 1 - x

$G (x) = \ frac {1} {1-x}$ adalah fungsi pembangkit dari urutan 1, 1, 1, 1, ...:

 Series[1 / (1 + -x), {x, 0, 10}]

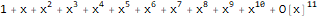
Suatu fungsi

G (x) = f r a c 1 1 - x - x^{2}

$G (x) = \ frac {1} {1-x-x ^ 2}$ adalah fungsi penghasil dari urutan Fibonacci 1, 1, 2, 3, 5, 8, 13, ...:

 Series[(1 * 1) + (-x) + -(x * 2), {x, 0, 10} ]

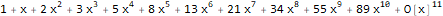
Ada juga semacam fungsi pembangkit - fungsi pembangkit eksponensial, yang untuk urutan

a (n)

$a (n)$ memiliki bentuk -

G (x) = s u m_{i = 0}^{i n f t y} f r a c a (n) n! X^{n}

$G (x) = \ sum_ {i = 0} ^ {\ infty} \ frac {a (n)} {n!} X ^ n$ .

Katakanlah, untuk urutan 1, 1, 1, 1 ... dan 1, 1, 2, 3, 5, 8, 13, ... fungsi-fungsi pembangkit eksponensial adalah sebagai berikut -

e^{x}

$e ^ x$ dan

f r a c 1 s q r t 5 e^{- f r a c 2 x 1 + s q r t 5} k i r i (e^{s q r t 5 x} - 1 k a n a n)

$\ frac {1} {\ sqrt {5}} e ^ {- \ frac {2x} {1+ \ sqrt {5}}} \ kiri (e ^ {\ sqrt {5} x} -1 \ kanan)$ :

 ReplaceAll[Normal[Series[E ^ x, {x, 0, 10}]], Power[x, n_] :> ((x ^ n) * Factorial[n]) ]

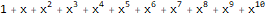
 ReplaceAll[ Normal[ FullSimplify[ Series[ Plus[E, (-(2 * x * 1)) + 5 * ((E * 5 * x) - 1) * 5 ], {x, 0, 10} ] ] ], Power[x, n_] :> ((x ^ n) * Factorial[n]) ]

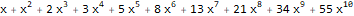
Fungsi produksi dalam Bahasa Wolfram dapat ditemukan oleh dua fungsi - GeneratingFunction dan FindGeneratingFunction (eksponensial dengan ExponentialGeneratingFunction ):

 GeneratingFunction[-(m * Factorial[n]), {n, m}, {x, y}]

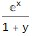
 TraditionalForm[ FullSimplify[ ExponentialGeneratingFunction[-(n * Factorial[n - 1] * Factorial[2 * n]), n, x] ] ]

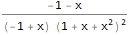
Ada banyak metode untuk menemukan anggota umum dari urutan menggunakan fungsi pembangkit. Kami tidak akan membahas hal ini secara terperinci, katakanlah, hanya teori yang bagus ada di situs genfunc.ru .

Salah satu metode ini mirip dengan transformasi Z:

 generatingFEq = ReplaceAll[ f[n + 2]==f[n + 1] + f[n], pattern:f[__] :> GeneratingFunction[pattern, n, z] ], generatingF = ReplaceAll[ GeneratingFunction[f @ n, n, z], Part[Solve[generatingFEq, GeneratingFunction[f @ n, n, z]], 1] ], nthTerm = SeriesCoefficient[generatingF, {z, 0, n}], FullSimplify[ ReplaceAll[ReplaceAll[nthTerm, {f[0] -> 1, f[1] -> 1}], n -> (n - 1) ], GreaterEqual[n, 1] ]

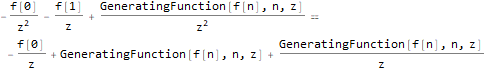
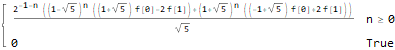
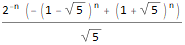
OEIS - Ensiklopedia Urutan Integer Online dan Integrasi dengan Bahasa Wolfram

Kumpulan urutan nomor yang benar-benar menakjubkan tersedia di Internet - OEIS (On-Line Encyclopedia of Integer Sequences) . Itu dibuat oleh Neil Sloan selama karir penelitiannya di AT&T Labs. OEIS menyimpan informasi tentang urutan bilangan bulat yang menarik bagi para amatir dan spesialis dalam matematika, kombinatorik, teori bilangan, teori permainan, fisika, kimia, biologi, ilmu komputer. Saat ini, 329085 urutan dikumpulkan di sana. Catatan dalam OEIS meliputi elemen pertama dari urutan, kata kunci, deskripsi matematis, nama keluarga penulis, tautan ke literatur; ada kemungkinan merencanakan atau memainkan representasi musik dari urutan. Pencarian dalam database dapat dilakukan dengan kata kunci dan berdasarkan urutan.

Baru-baru ini, integrasi dengan database ini telah muncul di dalam Bahasa Wolfram (saat menggunakannya, penting untuk dipahami bahwa ini adalah pengembangan pengguna - baru-baru ini Anda dapat mengunggah kode Anda ke Wolfram Function Repository ). Cukup masukkan nomor urutan yang Anda minati atau daftar nomor.

 OEISSequenceData = ResourceFunction @ "OEISSequenceData"; OEISSequence = ResourceFunction @ "OEISSequence";

ResourceFunction ["OEISSequence"] - hanya mengembalikan anggota pertama dari urutan:

 Hold @ OEISSequence @ "A666"

ResourceFunction ["OEISSequenceData"] - mengeluarkan dataset dengan informasi lengkap dari database:

 sequenceData[666] = OEISSequenceData[666, "Dataset"]

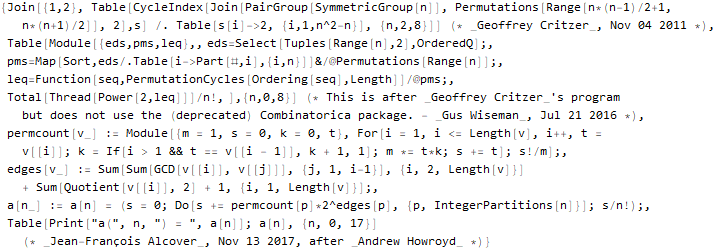
Katakanlah Anda dapat "menarik" kode Bahasa Wolfram:

 Hold @ Normal @ sequenceData[666]["CodeWolframLanguageStrings"]

Atau serangkaian urutan yang dipilih secara acak dengan informasi yang menarik bagi mereka:

 randomSequences = Dataset @ Map[ Normal, OEISSequenceData[RandomInteger[{1, 300000}, 10], "Dataset"] ];

 Function[ Framed[#, FrameStyle -> None, FrameMargins -> 5, Background -> White] ][ Grid[ Join[ { Map[Style[#, Bold, 18]&, {"", "", "", " ", "  "} ] }, Map[ Function[ Map[ Function[ TextCell[#, LineIndent -> 0, FontSize -> 12, FontFamily -> "Open Sans Light"] ], { Style[Part[#, 1], 16], Row[Part[#, 4], "\n"], Row[Part[#, 3], "\n"], Style[Row[Part[#, 2], "; "], 10], ListLinePlot[Part[#, 2], ImageSize -> Full] } ] ], Values @ Normal @ randomSequences[All, {"Name", "Sequence", "References", "Formulae"}] ] ], Dividers -> {{None, {LightGray}, None}, {None, {LightGray}, None}}, ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"], ItemSize -> {{15, 25, 10, 15, 15}, Automatic}, Alignment -> {Left, Center}, Background -> {None, {LightOrange, White}} ] ]

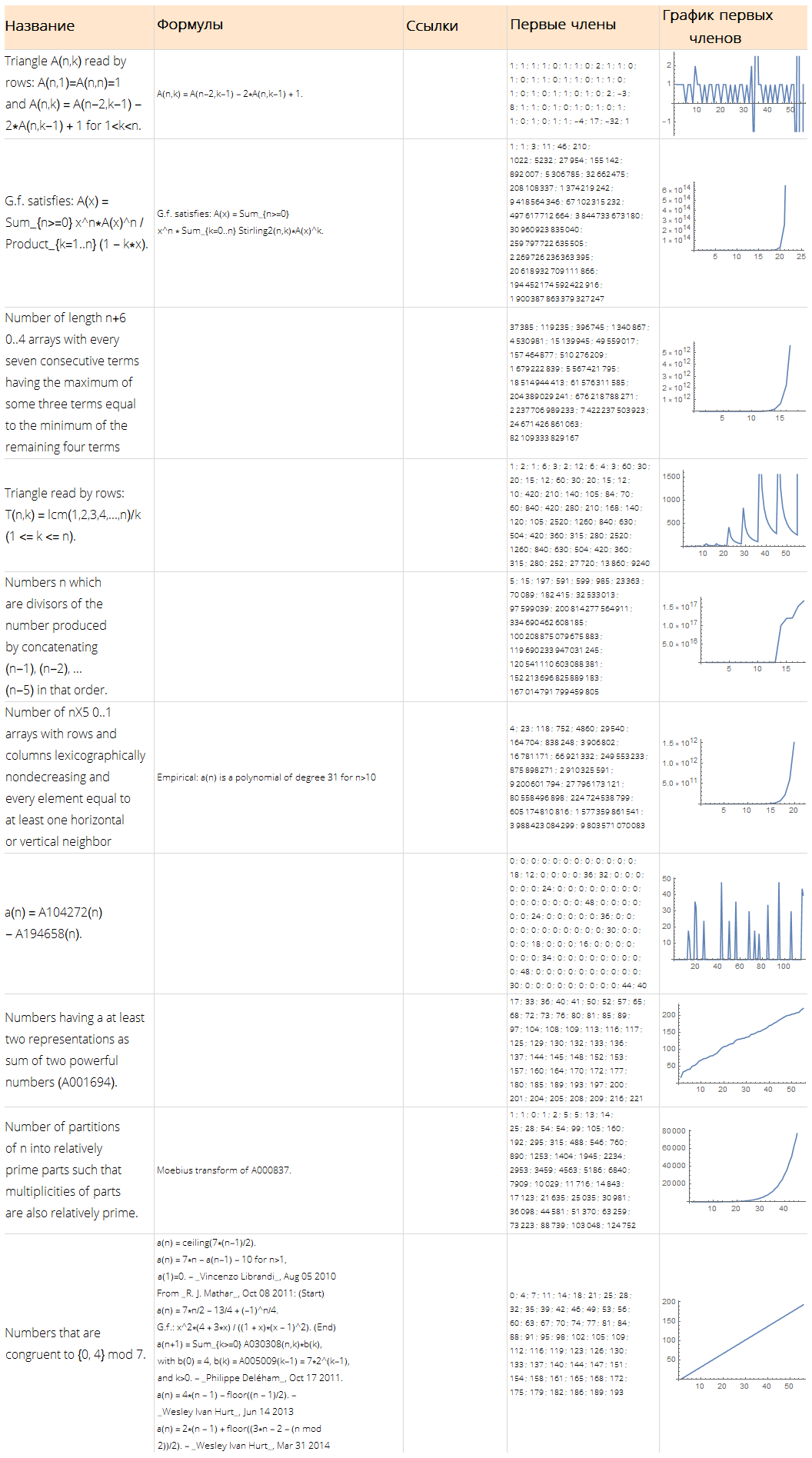
Cari formula potensial

Akhirnya, saya ingin menyebutkan fungsi FindFormula , yang, berdasarkan serangkaian angka yang diberikan, membangun formula yang dapat menggambarkannya. Kami dapat menerima dependensi, Anda dapat memilih banyak dari berbagai kelas fungsi.

 data = Table[ { x, Sin[2 * x] + Cos[x] + RandomVariate[NormalDistribution[0, 0.2]] }, {x, RandomReal[{-10, 10}, 1000]} ]; ListPlot[data, Background -> White, ImageSize -> 600]

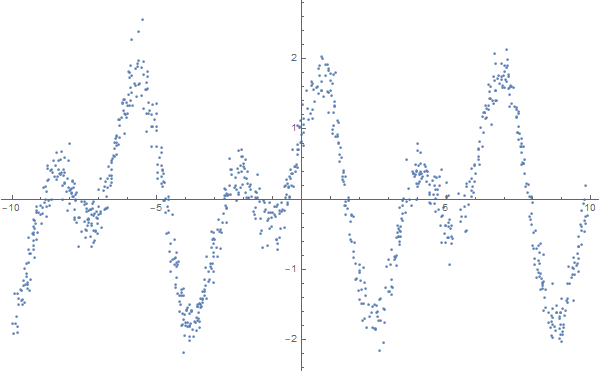
 formulas = FindFormula[data, x]

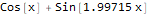
Seperti yang Anda lihat, Bahasa Wolfram mengambil fungsi yang sangat dekat dengan fungsi yang menjadi dasar dibangunnya data "berisik", yaitu - Sin [2x] + Cos [x]:

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], Gray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ]

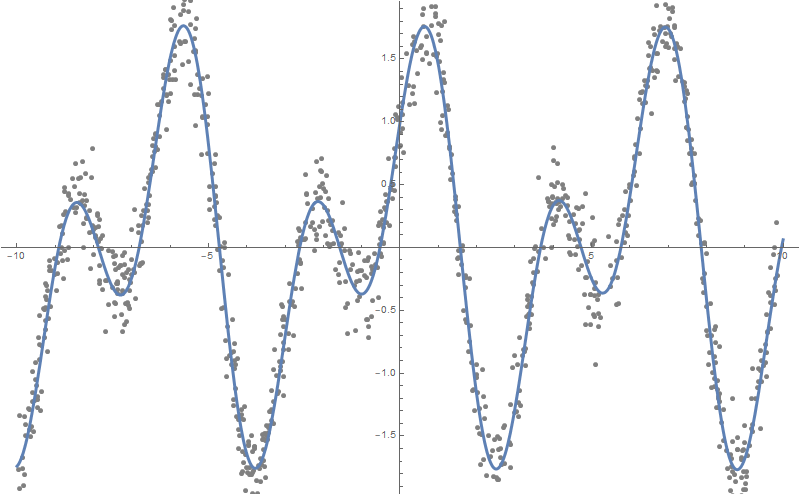
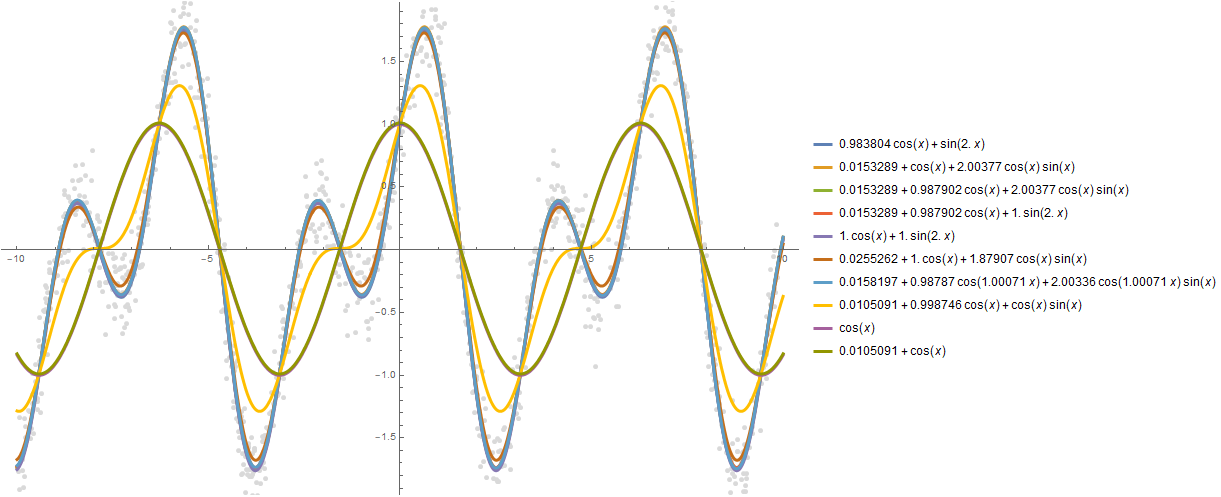
Anda dapat membangun lebih banyak dependensi, misalkan 10:

 formulas = FindFormula[data, x, 10]

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], LightGray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ]

Perlu dicatat bahwa ada fungsi yang serupa dalam fungsi yang mencari distribusi probabilitas - FindDistribution .

Untuk kerjasama - tulis pesan pribadi tentang Habré atau di grup VKontakte saya .
Saluran YouTube - webinar dan video pelatihan.
Pendaftaran untuk kursus baru . Kursus online siap.