"Cryptosystems Protocols": Diffie - Hellman, El-Gamal, MTI / A (0), STS

Seperti pencipta protokol tiga-pass dari bagian sebelumnya , para penulis algoritma berikut menganggapnya bukan hanya konstruksi matematika yang menyediakan beberapa operasi dasar (misalnya, enkripsi kunci publik), tetapi mencoba membangun sistem distribusi kunci lengkap di sekitar satu atau dua formula. Beberapa konstruksi ini, yang telah diubah, digunakan hingga saat ini (misalnya, protokol Diffie-Hellman), beberapa dari mereka hanya tersisa dalam sejarah kriptografi dan perlindungan informasi.

Kemudian pada 1990-an, primitif asimetris matematis (enkripsi dan tanda tangan elektronik) dan protokol akan dipisahkan, primitif ini akan digunakan, yang akan diperlihatkan pada bagian protokol asimetris.

Diffie - Hellman Protocol

Algoritma kunci publik pertama diusulkan oleh Diffie dan Hellman pada tahun 1976, "Arah Baru dalam Kriptografi" ( Bailey Whitfield Diffie, Martin Edward Hellman, "Arah baru dalam kriptografi" , [Diffie, Hellman 1976] ). Protokol ini, yang juga bisa disebut skema Diffie-Hellman , adalah yang pertama mengurangi persyaratan untuk saluran komunikasi untuk membangun koneksi yang aman tanpa bertukar kunci terlebih dahulu.

Protokol memungkinkan dua pihak untuk membuat kunci sesi umum menggunakan saluran komunikasi yang penyerang dapat dengarkan, tetapi dengan asumsi bahwa yang terakhir tidak dapat mengubah isi pesan.

Biarkan $$$p$- bilangan prima yang besar $$$g$- elemen primitif dari grup $$$\ mathbb {Z} _p ^ *$, $$$y = g ^ x \ bmod p$, dan $$$p$, $$$y$dan $$$g$diketahui sebelumnya. Fungsi $$$y = g ^ {x} \ bmod p$kami menganggap searah, yaitu, menghitung fungsi dengan nilai argumen yang diketahui adalah tugas yang mudah, dan inversinya (menemukan argumen) dengan nilai fungsi yang diketahui sulit. (Fungsi terbalik $$$x = \ log_g y \ bmod p$disebut fungsi logaritma diskrit. Saat ini tidak ada cara cepat untuk menghitung fungsi seperti itu untuk sederhana besar $$$p$.)

Protokol pertukaran terdiri dari tindakan berikut.

1. Alice memilih secara acak $$$2 \ leq a \ leq p - 1$
   $$$Alice \ to \ left \ {A = g ^ a \ bmod p \ right \} \ to Bob$
2. Bob memilih secara acak $$$2 \ leq b \ leq p-1$
   Bob menghitung kunci sesi $$$K = A ^ b \ bmod p$
   $$$Bob \ ke \ kiri \ {B = g ^ b \ bmod p \ right \} \ untuk Alice$
3. Alice menghitung $$$K = B ^ a \ bmod p$
   

Dengan cara ini, kunci sesi rahasia bersama dibuat $$$K$. Karena pemilihan nilai acak $$$a$dan $$$b$dalam sesi baru, kunci sesi baru akan diterima.

Protokol hanya menyediakan generasi kunci sesi baru (target G10). Dengan tidak adanya pihak tepercaya ketiga, itu tidak memberikan otentikasi dari para pihak (tujuan G1), karena kurangnya bagian dengan konfirmasi kepemilikan kunci, tidak ada otentikasi kunci (tujuan G8). Tetapi, karena protokol tidak menggunakan kunci "master" yang panjang, kita dapat mengatakan bahwa protokol tersebut memiliki properti kerahasiaan langsung yang sempurna (sasaran G9).

Protokol hanya dapat digunakan dengan saluran komunikasi di mana cryptanalyst aktif tidak dapat melakukan intervensi. Jika tidak, protokol menjadi rentan terhadap "serangan tengah" sederhana.

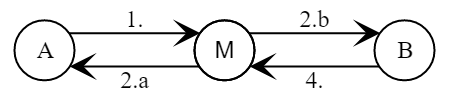
1. Alice memilih secara acak $$$2 \ leq a \ leq p - 1$
   $$$Alice \ to \ left \ {A = g ^ a \ bmod p \ right \} \ to Mellory ~ (Bob)$
2. Mallory memilih secara acak $$$2 \ leq m \ leq p-1$
   Mallory menghitung kunci sesi untuk saluran dengan Alice
   

   $$

   $$K_ {AM} = A ^ m \ bmod p = g ^ {am} \ bmod p$$
   
   $$$Mellory ~ (Alice) \ ke \ kiri \ {M = g ^ m \ bmod p \ kanan \} \ ke Bob$
   $$$Mellory ~ (Bob) \ ke \ kiri \ {M = g ^ m \ bmod p \ kanan \} \ ke Alice$
3. Alice menghitung kunci sesi untuk saluran dengan Mallory (berpikir bahwa Mallory adalah Bob)
   

   $$

   $$K_ {AM} = M ^ a \ bmod p = g ^ {am} \ bmod p$$
4. Bob memilih secara acak $$$2 \ leq b \ leq p-1$
   Bob menghitung kunci sesi untuk saluran dengan Mallory (berpikir bahwa Mallory adalah Alice)
   

   $$

   $$K_ {BM} = M ^ b \ bmod p = g ^ {bm} \ bmod p$$
   
   $$$Bob \ ke \ kiri \ {B = g ^ b \ bmod p \ right \} \ to Mellory ~ (Alice)$
5. Mallory menghitung kunci sesi untuk saluran dengan Bob
   

   $$

   $$K_ {BM} = B ^ m \ bmod p = g ^ {bm} \ bmod p$$
   
   

Akibatnya, Alice dan Bob menerima kunci sesi baru, tetapi mereka tidak membangun saluran komunikasi "aman" satu sama lain, tetapi dengan penyerang yang sekarang memiliki kemampuan untuk menyampaikan atau mengubah semua pesan yang dikirimkan antara Alice dan Bob.

Protokol Diffie-Hellman berbeda dari kebanyakan protokol distribusi utama karena fakta bahwa ia tidak menggunakan primitif kriptografi lainnya (enkripsi, tanda tangan digital atau fungsi hashing), tetapi dalam arti tertentu merupakan kriptografi yang primitif untuk membangun protokol yang lebih kompleks. Ini memberikan generasi nomor acak dalam sistem terdistribusi tanpa pusat tepercaya. Selain itu, tidak ada pihak yang dapat memaksa pihak lain untuk menggunakan kunci sesi lama, tidak seperti, misalnya, protokol Yahalom.

Protokol dapat diubah sehingga alih-alih kelompok multiplikasi dari perkalian sederhana, gunakan grup aditif penambahan titik dari kurva elips. Dalam hal ini, para pihak masih akan memilih beberapa bilangan bulat acak, tetapi jangan menaikkan angka generator menjadi kekuatan, tetapi gandakan titik generator dengan angka yang diinginkan.

1. Para pihak sepakat pada sekelompok titik kurva eliptik $$$\ mathbb {E}$subkelompok sikliknya $$$\ mathbb {G}$kekuatan $$$n = \ | \ mathbb {G} \ |$dan generator $$$G$kelompok $$$\ mathbb {G}$(atau setidaknya subkelompok yang cukup besar dari grup $$$\ mathbb {G}$)
2. Alice memilih secara acak $$$2 \ leq a \ leq n - 1$
   $$$Alice \ to \ left \ {A = a \ times G \ right \} \ to Bob$
3. Bob memilih secara acak $$$2 \ leq b \ leq n - 1$
   Bob menghitung poinnya $$$K = b \ kali A$
   $$$Bob \ ke \ kiri \ {B = g \ kali G \ right \} \ ke Alice$
4. Alice menghitung poinnya $$$K = a \ kali B$

Sebagai kunci sesi baru, para pihak dapat memilih, misalnya, koordinat pertama dari titik yang ditemukan $$$K$.

Protokol El Gamal

Protokol El-Gamal ( [ElGamal, 1984] , [ElGamal, 1985] ), karena distribusi awal kunci publik dari salah satu pihak, memberikan otentikasi kunci untuk sisi ini. Dapat dijamin bahwa hanya pemilik kunci pribadi yang sesuai yang dapat menghitung kunci sesi. Namun, konfirmasi penerimaan kunci (pemenuhan tujuan G1 dan G8) bukan bagian dari protokol.

1. Alice dan Bob memilih opsi umum $$$p$dan $$$g$dimana $$$p$Merupakan bilangan prima yang besar, dan $$$g$- elemen bidang primitif $$$\ mathbb {Z} _p ^ *$.
   Bob menciptakan sepasang kunci pribadi dan publik $$$b$dan $$$K_B$:
   

   $$

   $$\ begin {array} {l} b: 2 \ leq b \ leq p - 1, \\ K_B = g ^ b \ bmod p. \ end {array}$$
   
   Kunci publik $$$K_B$Itu adalah akses terbuka publik untuk semua pihak. Seorang cryptanalyst tidak dapat menggantikannya - substitusi akan terlihat.
2. Alice mengambil rahasia $$$x$dan menghitung kunci sesi $$$K$
   

   $$

   $$K = K_B ^ {x} = g ^ {bx} \ bmod hlm.$$
   
   

   $$

   $$Alice \ to \ left \ {g ^ x \ bmod p \ right \} \ to Bob$$
3. Bob menghitung kunci sesi
   

   $$

   $$K = (g ^ x) ^ {b} = g ^ {bx} \ bmod hlm.$$

Protokol tidak menjamin pemilihan kunci sesi baru di setiap sesi protokol (G10), dan penggunaan kunci "master" $$$K_B$untuk mentransfer kunci sesi memungkinkan penyerang menghitung semua kunci sesi dari sesi sebelumnya ketika kunci pribadi dikompromikan $$$b$(tujuan G9).

Protokol MTI / A (0)

Pada tahun 1986, C. Matsumoto ( Tsutomu Matsumoto ), I. Takashima ( Youichi Takashima ) dan H. Imai ( Hideki Imai ) mengusulkan beberapa algoritma, yang kemudian disebut keluarga protokol MTI ( [Matsumoto, Tsutomu, Imai 1986] ). Karena distribusi awal kunci publik dari kedua pihak, mereka memberikan otentikasi kunci implisit (target G7). Artinya, kunci sesi hanya dapat dijamin untuk diterima oleh pemilik kunci publik yang sesuai. Kami akan mempertimbangkan salah satu perwakilan keluarga ini - protokol MTI / A (0).

Sebelumnya, para pihak menyepakati parameter umum sistem. $$$p$dan $$$g$dimana $$$p$Merupakan bilangan prima yang besar, dan $$$g$- elemen bidang primitif $$$\ mathbb {Z} _p ^ *$.


Masing-masing pihak (Alice dan Bob) menghasilkan sepasang kunci pribadi dan publik:

$$

$$\ begin {array} {ll} Alice: & ~ a, ~~ K_A = g ^ a \ bmod p, \\ Bob: & ~ b, ~~ K_B = g ^ b \ bmod p. \\ \ end {array}$$

1. Alice menghasilkan angka acak $$$R_A: ~ 2 \ leq R_A \ leq p-1$
   $$$Alice \ to \ left \ {g ^ {R_A} \ bmod p \ right \} \ to Bob$
2. Bob menghasilkan angka acak $$$R_B: ~ 2 \ leq R_B \ leq p-1$
   Bob menemukan kunci sesi $$$K = (g ^ {R_A}) ^ b \ cdot K_A ^ {R_B} \ bmod p$
   $$$Bob \ ke \ kiri \ {g ^ {R_B} \ bmod p \ right \} \ ke Alice$
3. Alice menghitung kunci sesi $$$K = (g ^ {R_B}) ^ a \ cdot K_B ^ {R_A} \ bmod p$

Jika kunci publik $$$K_A$dan $$$K_B$cocokkan dengan kunci pribadi Anda $$$a$dan $$$b$, lalu kunci sesi dihitung oleh peserta yang cocok:

$$

$$\ begin {array} {lll} (g ^ {R_A}) ^ b \ cdot K_A ^ {R_B} \ bmod p & = & g ^ {b R_A + a R_B} \ bmod p, \\ (g ^ { R_B}) ^ a \ cdot K_B ^ {R_A} \ bmod p & = & g ^ {a R_B + b R_A} \ bmod p. \ end {array}$$

Karena kompleksitas tugas logaritma diskrit, penyerang tidak akan dapat memperoleh $$$a, R_A$atau $$$b, R_B$dari pesan yang dikirimkan, dan publikasi awal kunci publik memastikan bahwa hanya pengguna yang sah yang menerima kunci sesi. Pilihan acak $$$R_A$dan $$$R_B$memastikan bahwa kedua pihak dapat memastikan untuk membuat kunci sesi baru di setiap sesi protokol.

Seperti perwakilan protokol cryptosystem lainnya, MTI tidak dikembangkan dengan mempertimbangkan kemungkinan kompromi kunci "master" tertutup. $$$a$dan $$$b$(tujuan G9).

Protokol Stasiun-ke-Stasiun

Protokol STS ( Station-to-Station , [Diffie, Oorschot, Wiener 1992] ) dimaksudkan untuk sistem komunikasi seluler. Ia menggunakan ide-ide protokol Diffie-Hellman dan kriptosistem RSA. Fitur protokol adalah penggunaan mekanisme tanda tangan elektronik untuk saling otentikasi para pihak.

Sebelumnya, para pihak menyepakati parameter umum sistem. $$$p$dan $$$g$dimana $$$p$Merupakan bilangan prima yang besar, dan $$$g$- elemen bidang primitif $$$\ mathbb {Z} _p ^ *$.

Setiap sisi $$$A$dan $$$B$memiliki pasangan kunci jangka panjang: kunci pribadi untuk mendekripsi dan membuat tanda tangan elektronik $$$K _ {\ text {public}}$dan kunci publik untuk enkripsi dan verifikasi tanda tangan $$$K _ {\ text {public}}$.

$$

$$\ begin {array} {ll} A: K_ {A, \ text {private}}, K_ {A, \ text {public}}: \ forall M: & \ text {Verifikasi} _A (M, S_A (M )) = true, \\ & D_A (E_A (M)) = M, \\ B: K_ {B, \ text {private}}, K_ {B, \ text {public}}: \ forall M: & \ text {Verify} _B (M, S_B (M)) = true, \\ & D_B (E_B (M)) = M. \\ \ end {array}$$

Dimana $$$\ text {Verify} _A (\ dots)$itu adalah fungsi memeriksa tanda tangan elektronik pada kunci publik $$$K_ {A, \ text {public}}$, dan $$$D_A$- Fungsi dekripsi menggunakan kunci pribadi $$$K_ {A, \ text {private}}$.

Protokol terdiri dari empat lintasan, tiga di antaranya termasuk transmisi pesan ( [Cheryomushkin 2009] ).

1. Alice mengambil nomor acak $$$R_A: 2 \ leq R_A \ leq p-1$.
   $$$Alice \ ke \ left \ {A, m_A = g ^ {R_A} \ bmod p \ right \} \ to Bob$
2. Bob mengambil nomor acak $$$R_B: 2 \ leq R_B \ leq p-1$.
   Bob menghitung kunci sesi $$$K = m_A ^ {R_B} \ bmod p$.
   $$$Bob \ ke \ kiri \ {B, A, m_B = g ^ {R_B} \ bmod p, E_K (S_B (m_A, m_B)) \ kanan \} \ untuk Alice$
3. Alice menghitung kunci sesi $$$K = m_B ^ {R_A} \ bmod p$.
   Alice memverifikasi tanda tangan di pesan $$$E_K (S_B (m_A, m_B))$.
   $$$Alice \ ke \ left \ {A, B, E_K (S_A (m_A, m_B)) \ right \} \ to Bob$
4. Bob memverifikasi tanda tangan dalam pesan itu $$$E_K (S_A (m_A, m_B))$.

Protokol ini memberikan jaminan pembuatan kunci baru (G10), tetapi kerahasiaan langsung tidak sempurna (G9).

Seperti yang ditunjukkan oleh serangan Lowe 1996 ( [Lowe 1996] ), protokol tidak dapat menjamin otentikasi subyek (target G1), kunci (G7), dan bukti kepemilikan kunci sesi (G8). Meskipun penyerang tidak dapat memperoleh akses ke kunci sesi baru jika protokol tersebut hanya digunakan untuk mengotentikasi subjek, Alice dapat mengira penyerang untuk Bob.

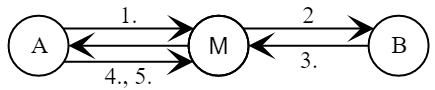
1. Alice mengambil nomor acak $$$R_A: 2 \ leq R_A \ leq p-1$.
   $$$Alice \ ke \ left \ {A, m_A = g ^ {R_A} \ bmod p \ right \} \ to Mellory ~ (Bob)$
   
2. $$$Mellory \ ke \ left \ {M, m_A \ right \} \ ke Bob$
   
3. Bob mengambil nomor acak $$$R_B: 2 \ leq R_B \ leq p-1$.
   Bob menghitung kunci sesi $$$K = m_A ^ {R_B} \ bmod p$.
   $$$Bob \ ke \ kiri \ {B, M, m_B, E_K (S_B (m_A, m_B)) \ kanan \} \ ke Mellory$
   
4. $$$Mellory ~ (Bob) \ ke \ left \ {B, A, E_K (S_B (m_A, m_B)) \ right \} \ ke Alice$
   
5. Alice menghitung kunci sesi $$$K = m_B ^ {R_A} \ bmod p$.
   Alice memverifikasi tanda tangan di pesan $$$E_K (S_B (m_A, m_B))$.
   $$$Alice \ ke \ left \ {A, B, E_K (S_A (m_A, m_B)) \ right \} \ to Mellory ~ (Bob)$
   

Setelah berhasil menyelesaikan protokol, Alice yakin bahwa dia berbicara dengan Bob.

Seperti semua "cryptosystem-protocols" lainnya, protokol Station-to-Station didasarkan pada beberapa sumber informasi eksternal tentang kunci publik dari para peserta, tanpa mempertanyakan kebenaran dan keandalan sumber ini. Yang, dalam kasus umum, salah. Jika informasi tentang kunci peserta perlu diterima secara eksternal pada setiap sesi protokol (misalnya, jika ada banyak peserta dan tidak ada kemungkinan untuk mengingat kunci semua), maka saluran untuk mendapatkan kunci publik akan menjadi tujuan utama dari cryptanalyst aktif untuk protokol yang dipertimbangkan. Cara melindungi diri Anda dari penggunaan kriptografi asimetris primitif ini ada di bagian selanjutnya.

Sastra

• [Diffie, Hellman 1976] Diffie W., Hellman ME Arah baru dalam kriptografi // Teori Informasi, Transaksi IEEE aktif. - 1976. - November - t. 22, No. 6. - hal. 644-654. - ISSN 0018-9448. - DOI: 10.1109 / TIT.1976.1055638.
• [ElGamal, 1984] El Gamal T. A Cryptosystem Kunci Publik dan Skema Tanda Tangan Berdasarkan Logaritma Diskrit // Prosiding CRYPTO 84 tentang Kemajuan dalam Kriptologi. - Santa Barbara, California, AS: Springer-Verlag New York, Inc., 1985 .-- hlm. 10-18. - ISBN 0-387-15658-5. - URL: dl.acm.org/citation.cfm?id=19478.19480 .
• [ElGamal, 1985] El Gamal T. Sebuah cryptosystem kunci publik dan skema tanda tangan berdasarkan logaritma diskrit // Transaksi IEEE tentang Teori Informasi. - 1985. - Juli. - t. 31, No. 4. - hal. 469-472. - DOI: 10.1109 / TIT.1985.1057074.
• [Matsumoto, Tsutomu, Imai 1986] Matsumoto T., Takashima Y., Imai H. Sedang mencari sistem distribusi publickey yang cerdas // Trans. Inst. Elektron Komunal. Eng Jpn. Sekte E. T. 69. masalah 2. - 02.1986. - dengan 99-106.
• [Diffie, Oorschot, Wiener 1992] Diffie W., PC Van Oorschot, Otentikasi Wiener MJ
  dan pertukaran kunci terotentikasi // Desain, Kode, dan Kriptografi. - 1992. - Juni. - t. 2, No. 2. - hal. 107-125. - ISSN 1573-7586. - DOI: 10.1007 / BF00124891.
• [Lowe 1996] Lowe G. Beberapa serangan baru terhadap protokol keamanan // CSFW '96 Prosiding lokakarya IEEE ke-9 tentang Yayasan Keamanan Komputer. —Washington, DC, AS: IEEE Computer Society, 1996. - hlm. 162.
• [Cheremushkin 2009] Cheremushkin A. V. Protokol kriptografi: sifat dasar dan kerentanan // Matematika Diskrit Terapan. - 2009. - November - masalah. 2. - hal. 115-150. - URL: cyberleninka.ru/article/n/kriptograficheskieprotokoly-osnovnye-svoystva-i-uyazvimosti.pdf .