Dua karya monumental meyakinkan banyak ahli matematika untuk meninggalkan tanda yang sama. Tujuan mereka adalah merekonstruksi fondasi disiplin dengan bantuan hubungan yang lebih lemah - “kesetaraan”. Dan proses ini tidak selalu berjalan lancar.
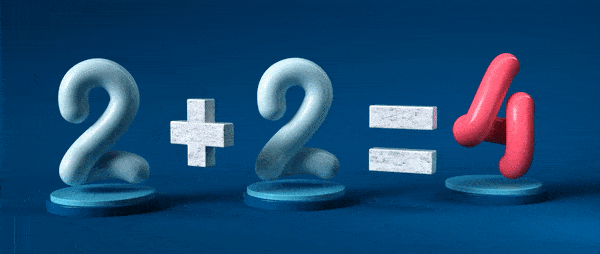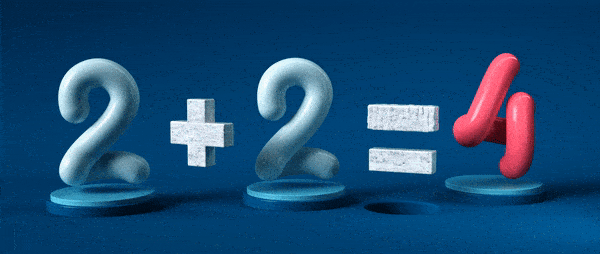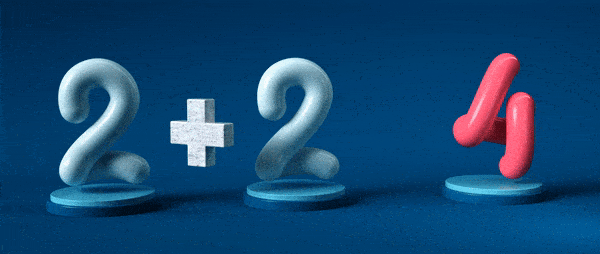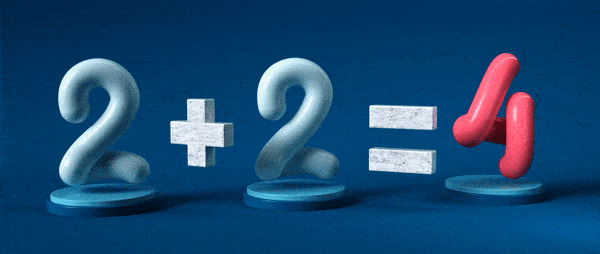
Tanda sama adalah landasan matematika. Dia tampaknya membuat pernyataan yang fundamental dan konsisten: kedua entitas ini persis sama.
Namun, lingkaran matematikawan tumbuh, mengacu pada tanda sama dengan, seperti kesalahan awal matematika. Mereka menganggap itu sebagai gloss eksternal, menyembunyikan kesulitan penting dari hubungan kuantitas - kesulitan yang dapat membuka solusi untuk sejumlah besar masalah. Mereka ingin mereformasi matematika menggunakan bahasa kesetaraan yang lebih longgar.
"Kami menelurkan ide kesetaraan ini," kata
Jonathan Campbell dari Duke University. "Dan seharusnya ada kesetaraan di tempatnya."
Sosok yang paling menonjol di komunitas ini adalah
Jacob Lurie . Pada bulan Juli,
Lurie yang berusia 41 tahun mengundurkan diri sebagai karyawan penuh waktu di Harvard untuk posisi fakultas di Institut Princeton untuk Studi Lanjutan, di mana beberapa ahli matematika terkemuka di dunia bekerja.
Gagasan dengan skala seperti Lurie jarang ditemukan di bidang apa pun. Dalam buku-bukunya yang membentang ribuan halaman penuh dengan rincian teknis, ia menciptakan cara yang sangat berbeda dari cara biasa memahami konsep matematika paling dasar, melampaui tanda yang sama. "Saya pikir itu baginya bahwa ini adalah cara berpikir yang benar tentang matematika," kata
Michael Hopkins , seorang matematikawan Harvard dan kepala sekolah pascasarjana.
Dia menerbitkan buku pertamanya,
Theory of Higher Topos , pada tahun 2009. Volume 944 halaman berfungsi sebagai instruksi untuk menafsirkan bidang matematika yang dikenal dalam bahasa baru "kategori tak terbatas." Pada tahun-tahun berikutnya, ide-ide Lurie menembus berbagai disiplin ilmu matematika. Banyak ahli matematika menganggap mereka sangat diperlukan untuk masa depan bidang ini. "Tidak ada yang akan sama setelah mempelajari kategori tak terhingga," kata
John Francis dari Northwestern University,
Jacob LurieNamun, penyebaran kategori tak terhingga mengungkapkan semua masalah yang dilalui oleh bidang matematika yang dihormati, mencoba menyerap ide-ide baru yang berani - terutama ide yang menantang konsep terpentingnya. "Ada tingkat konservatisme tertentu dalam komunitas matematika," kata
Clark Barwick dari Universitas Edinburgh. "Saya tidak berpikir bahwa kelompok matematika mana pun dapat diharapkan untuk dengan cepat menerima alat apa pun tanpa alasan yang meyakinkan."
Meskipun banyak ahli matematika telah menerima kategori tak terhingga, hanya sedikit yang membaca seluruh teks Lurie yang panjang dan sangat abstrak. Akibatnya, bagian dari pekerjaan berdasarkan ide-idenya ternyata menjadi kurang ketat daripada yang diterima dalam matematika.
"Saya mendengar orang berkata: 'Lurie memilikinya di suatu tempat,'" kata
Inna Zakharevich , seorang ahli matematika di Cornell University. - Dan saya katakan: 'Benarkah? Anda merujuk pada 8.000 halaman teks. ' Ini bukan referensi, ini banding ke otoritas. "
Matematikawan masih berusaha mewujudkan luasnya gagasan Lurie dan cara unik untuk mempresentasikannya. Mereka mengekstrak esensi dari presentasinya tentang kategori-kategori infinity dan menyajikannya dalam paket baru sehingga lebih banyak ahli matematika dapat menggunakannya. Dalam arti tertentu, mereka menjalankan kepemimpinan yang diperlukan, yang wajib mengikuti revolusi apa pun, menerjemahkan teks revolusioner ke dalam kode hukum sehari-hari. Dengan demikian, mereka menciptakan masa depan matematikawan, tidak didasarkan pada kesetaraan, tetapi pada kesetaraan.
Menara kesetaraan tak berujung
Kesetaraan matematika tampaknya paling tidak kontroversial dari semua ide. Dua manik-manik ditambah satu manik sama dengan tiga manik-manik. Apa lagi yang bisa dibicarakan? Namun, ide-ide paling sederhana bisa menjadi yang paling menipu.
Sejak akhir abad ke-19, dasar-dasar matematika telah dibangun di atas set objek yang disebut set. Teori himpunan menetapkan aturan, atau aksioma, untuk penciptaan dan penanganan himpunan ini. Salah satu aksioma ini, misalnya, mengklaim bahwa Anda dapat menambahkan satu set elemen ke set dua elemen dan mendapatkan set baru tiga elemen: 2 + 1 = 3.
Cara formal untuk menunjukkan kesetaraan dua kuantitas adalah untuk mencocokkan pasangan satu sama lain. Cocokkan satu manik di sebelah kanan tanda sama dengan satu manik di sebelah kiri. Setelah semua perbandingan, tidak akan ada manik-manik tambahan yang tersisa.
Teori himpunan mengakui bahwa dua set dari tiga objek masing-masing dapat secara tepat dicocokkan satu sama lain, tetapi tidak berarti semua cara yang mungkin berbeda dari perbandingan semacam itu. Manik pertama di sebelah kanan dapat mengambil sepasang dalam bentuk manik pertama di sebelah kiri, atau mencocokkan yang pertama di sebelah kanan dengan yang kedua di sebelah kiri, dan seterusnya (bisa ada enam pasang seperti itu). Mengatakan bahwa dua tambah satu sama dengan tiga, dan mengakhiri ini berarti tidak melihat semua cara yang mungkin untuk menyamakan mereka. "Masalahnya adalah bahwa ada banyak cara untuk berpasangan," kata Campbell. "Dan kita melupakan mereka ketika kita mengatakan kesetaraan."
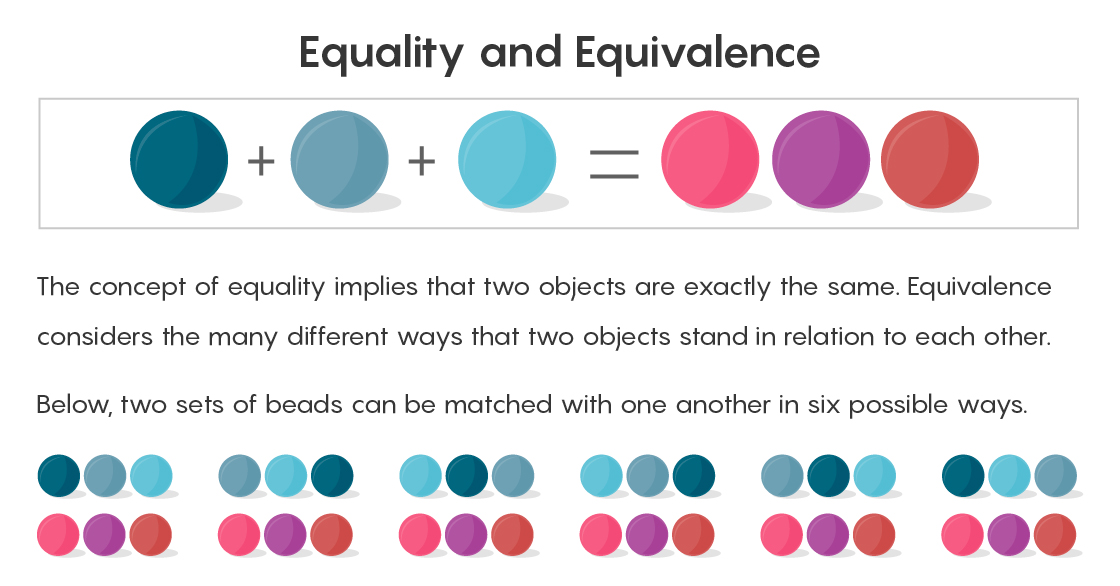
Di sinilah kesetaraan berperan. Jika persamaan adalah hubungan yang jelas - dua hal sama atau tidak - kesetaraan bisa berbeda.
Saat Anda secara tepat mencocokkan setiap elemen dari satu set dengan setiap elemen lainnya, Anda mendapatkan kesetaraan yang kuat. Tetapi, misalnya, dalam bidang matematika seperti
homotopy , dua bentuk (atau angka geometris) adalah setara jika seseorang dapat ditransformasikan menjadi yang lain dengan meregangkan atau mengompres tanpa putus.
Dari sudut pandang teori homotopy, cakram datar dan titik dalam ruang adalah ekuivalen - cakram dapat dikompresi ke titik. Namun, Anda tidak dapat mencocokkan titik pada disk dengan titik pada titik. Memang, disk poin memiliki angka tak terbatas, dan satu poin hanyalah satu poin.
Sejak pertengahan abad ke-20, matematikawan telah berusaha mengembangkan alternatif untuk menetapkan teori di mana matematika akan lebih mudah ditangani dalam hal kesetaraan. Pada tahun 1945, ahli matematika
Samuel Eileberg dan
Saunders MacLane memperkenalkan objek fundamental baru dengan persamaan
bawaan . Mereka menyebutnya kategori.
Suatu kategori dapat diisi dengan apa saja. Anda dapat mengambil kategori mamalia, yang akan mencakup semua makhluk berdarah panas berbulu yang menghasilkan susu. Atau Anda dapat membuat kategori objek matematika: set, bentuk geometris, atau sistem numerik.
Kategori adalah himpunan dengan metadata tambahan: deskripsi semua cara untuk mencocokkan satu objek dengan yang lain, yang mencakup deskripsi semua fitur yang dapat dianggap setara oleh dua objek. Kategori juga dapat dibayangkan sebagai objek geometris di mana setiap elemen kategori diwakili oleh sebuah titik.
Bayangkan, misalnya, permukaan bola. Setiap titik pada permukaan ini dapat menunjukkan jenis segitiga. Jalur antara titik mengekspresikan hubungan ekivalensi antara objek. Dari sudut pandang teori kategori, kita lupa cara spesifik untuk menggambarkan suatu objek dan alih-alih berkonsentrasi pada tempat yang ditempati objek tersebut dalam kaitannya dengan semua objek lain dari jenis ini.
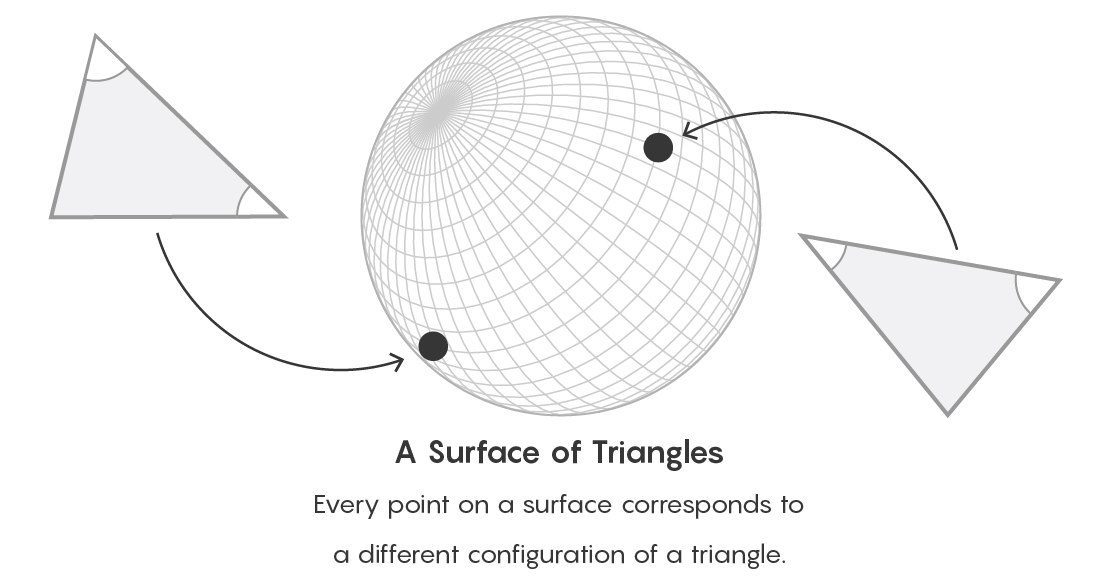Setiap titik di permukaan sesuai dengan jenis segitiga tertentu."Kami memperlakukan banyak hal sebagai hal, meskipun dalam kenyataannya mereka adalah hubungan antara banyak hal," kata Zakharevich. - Frasa "suamiku" berarti sesuatu yang kita anggap sebagai objek, tetapi Anda dapat menganggapnya sebagai suatu hubungan. Bagian tertentu dari itu ditentukan oleh hubungan dengan saya. "
Versi kategori dari Eilenberg dan MacLane sangat cocok untuk bekerja dengan opsi kesetaraan yang kuat. Tetapi pada paruh kedua abad ke-20, matematikawan semakin menggunakan bentuk-bentuk ekivalensi yang lebih lemah, seperti homotopy. "Matematika menjadi lebih halus, dan mau tidak mau kita memiliki keinginan untuk ide-ide yang lebih halus tentang hal-hal biasa," kata Emily Riel, seorang ahli matematika di Universitas Johns Hopkins. Dalam versi kesetaraan yang lebih halus ini, jumlah informasi tentang hubungan antara dua objek meningkat tajam. Kategori dasar Eilenberg dan MacLane tidak dimaksudkan untuk ini.
Untuk melihat peningkatan jumlah informasi, pertama-tama ingatlah lingkup kita, yang menunjukkan segitiga yang berbeda. Dua segitiga secara homogen sama jika satu dapat ditransformasikan menjadi yang lain dengan peregangan atau deformasi lainnya. Dua titik pada suatu permukaan secara homogen sama jika ada jalur yang menghubungkannya. Dengan mempelajari jalur homotop antara titik-titik pada suatu permukaan, Anda sebenarnya mempelajari berbagai cara berbeda bahwa segitiga yang dilambangkan dengan titik-titik ini saling terhubung satu sama lain.
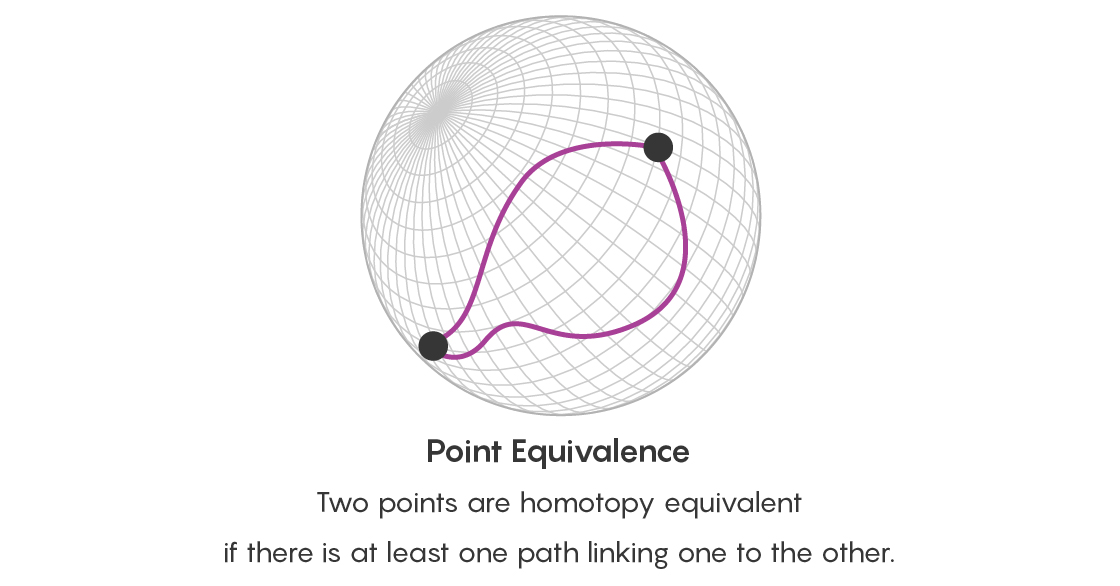
Namun, tidak cukup untuk menyatakan bahwa dua titik terhubung dalam banyak cara yang setara. Penting juga untuk memikirkan kesetaraan semua jalan ini. Oleh karena itu, selain pertanyaan tentang kesetaraan poin, sekarang Anda mengajukan pertanyaan tentang kesetaraan dari dua jalur yang dimulai dan berakhir pada titik yang sama - dan apakah ada jalur yang menghubungkan jalur ini. Jalur ini yang menghubungkan jalur tersebut berbentuk cakram, yang batasnya adalah dua jalur ini.
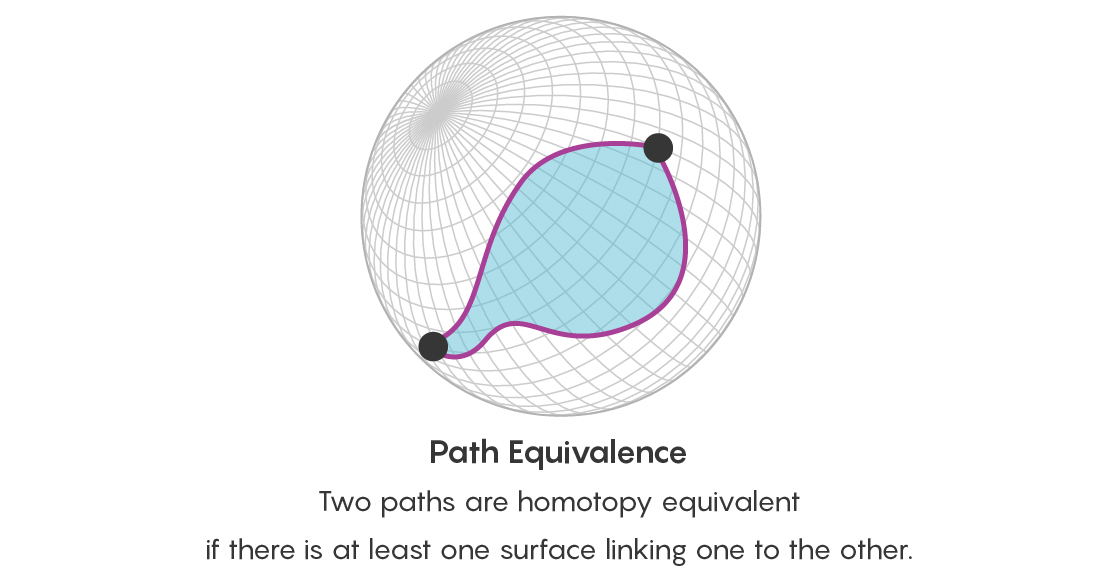
Anda dapat mengembangkan ide ini lebih lanjut. Dua disk setara jika dihubungkan oleh jalur - dan jalur ini akan berbentuk objek tiga dimensi. Objek tiga dimensi seperti itu sendiri dapat dihubungkan oleh jalur empat dimensi (jalur antara dua objek selalu memiliki satu dimensi lebih dari objek itu sendiri).
Akibatnya, Anda membangun menara kesetaraan tak berujung antara ekuivalensi. Berdebat tentang keseluruhan doktrin, Anda menghasilkan pandangan umum dari semua objek yang telah Anda tandai dengan titik-titik di bola.
"Ini hanya sebuah bola, tetapi ternyata untuk memahami bentuk bola, Anda harus pergi hingga tak terbatas dengan cara tertentu," kata
David Ben-Zvi dari University of Texas di Austin.
Dalam dekade terakhir abad ke-20, banyak ahli matematika telah bekerja pada teori "kategori ketidakterbatasan" - pada apa yang mampu melacak menara tak terbatas kesetaraan antara kesetaraan. Beberapa dari mereka telah mencapai kesuksesan serius. Tetapi hanya satu yang mencapai akhir.
Menulis ulang Matematika
Karya pertama Jacob Lurie dalam kategori infinity tidak terlalu berhasil. Pada 5 Juni 2003, ilmuwan berusia 25 tahun itu menerbitkan dokumen setebal 60 halaman berjudul "
On the Topos of Infinity " di situs pracetak ilmiah arxiv.org. Di sana ia mulai membuat draf kasar aturan yang dengannya matematikawan dapat bekerja dengan kategori tak terhingga.
Tidak semua orang menerima karya pertama dengan cara yang sama. Tak lama setelah membaca,
Peter May , seorang ahli matematika di University of Chicago, menulis kepada atasan Lurie, Michael Hopkins, bahwa meskipun karya Lurie mengandung ide-ide menarik, itu terlihat belum selesai dan memerlukan pendekatan yang lebih disiplin.
"Aku menjelaskan komentar kita kepada Mike, dan dia meneruskannya pada Jacob," kata May.
Masih belum diketahui apakah Lurie menganggap surat May sebagai tantangan, atau apakah ia sudah merencanakan langkah selanjutnya (Lurie menolak banyak permintaan wawancara). Jelas bahwa setelah menerima komentar kritis, Lurie mencapai periode produktivitas multi-tahun, yang kemudian menjadi legendaris.
"Saya tidak bisa masuk ke otak Jacob, dan karena itu saya tidak tahu persis apa yang dipikirkannya," kata May. "Tapi ada perbedaan besar antara konsep yang kami ulas dan versi final, yang sudah pada tingkat matematika yang sama sekali berbeda."
Pada tahun 2006, Lurie memposting di arxiv.org sebuah konsep "Theories of Highestos Topos". Dalam karya monumental ini, ia menciptakan alat yang diperlukan untuk mengganti teori himpunan dengan basis baru untuk matematika berdasarkan kategori tak terhingga. “Dia menciptakan ribuan halaman perangkat fundamental ini yang kita semua gunakan sekarang,” kata Charles Rezk, seorang ahli matematika di University of Illinois di Urbana-Champaign, yang melakukan pekerjaan penting sejak awal dalam mengembangkan kategori infinity. "Saya tidak bisa membayangkan bagaimana mungkin membuat karya seperti 'Teori Topos Tertinggi' seumur hidup - dan dia menciptakannya dalam dua atau tiga tahun."
Kemudian pada tahun 2011, Lurie memberi pekerjaan lain yang lebih lama. Di dalamnya, ia menemukan kembali aljabar.
Aljabar memberi kita seperangkat aturan formal yang luar biasa untuk memanipulasi persamaan. Matematikawan terus-menerus menggunakan aturan ini untuk membuktikan teorema. Namun, aljabar melakukan senam di bar tetap dengan tanda sama. Hapus bilah ini, ganti dengan konsep kesetaraan yang lebih singkat, dan beberapa operasi akan menjadi sangat rumit.
Ambil salah satu aturan aljabar pertama yang dipelajari anak-anak di sekolah: asosiatif. Jumlah atau produk dari tiga angka atau lebih tidak tergantung pada pengelompokannya: 2 × (3 × 4) = (2 × 3) × 4.
Sangat mudah untuk membuktikan properti associativity untuk daftar tiga angka atau lebih jika Anda bekerja dengan kesetaraan. Ini sulit ketika Anda bekerja bahkan dengan konsep kesetaraan yang kuat. Tetapi ketika Anda beralih ke versi kesetaraan yang lebih halus, dengan menara jalurnya yang tak berujung yang menghubungkan jalur, bahkan aturan sederhana, mirip dengan asosiatif, berubah menjadi hutan gelap.
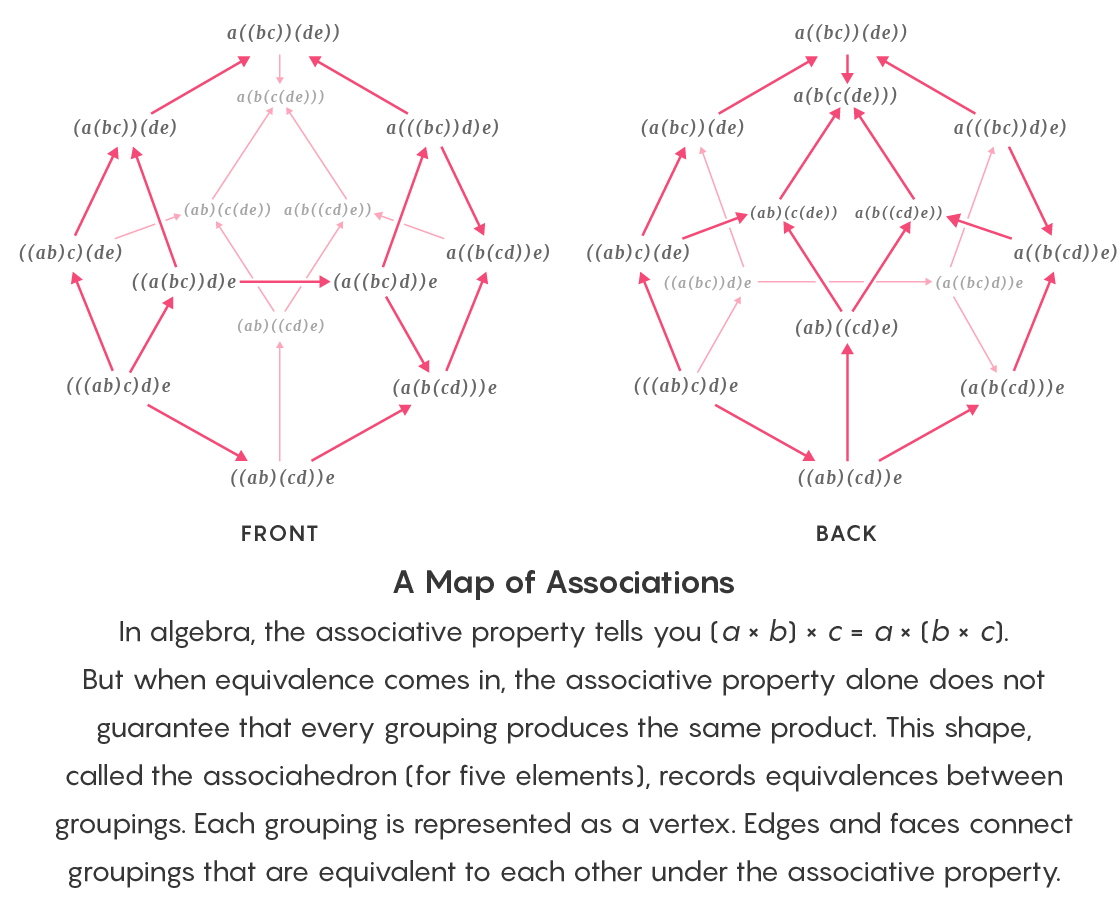Dalam aljabar, asosiasi menyatakan bahwa (a × b) × c = a × (b × c). Tetapi dengan penggunaan kesetaraan, asosiatif saja tidak menjamin bahwa pengelompokan unsur apa pun akan menghasilkan hasil penggandaan yang sama. Assocahedron ini berisi catatan kesetaraan grup. Setiap titik berhubungan dengan pengelompokan. Tepi dan wajah menggabungkan kelompok yang secara asosiatif setara satu sama lain."Ini membuat masalah menjadi sangat rumit, yang membuatnya tidak mungkin untuk bekerja dengan versi matematika yang baru ini," kata David Isla, seorang ahli matematika di University of Montana.
Dalam Aljabar Tinggi, versi terbaru yang membentang lebih dari 1553 halaman, Lurie mengembangkan opsi asosiatif untuk kategori tak terhingga - serta banyak teorema aljabar lainnya yang bersama-sama membentuk dasar matematika kesetaraan.
Dua buku ini menghasilkan efek bom yang meledak; karya-karya semacam itu memunculkan revolusi ilmiah. “Skalanya luar biasa,” kata Reel. "Itu adalah pencapaian level
Grothendieck dalam geometri aljabar."
Namun, revolusi membutuhkan waktu, dan, ketika matematikawan menemukan setelah penerbitan buku-buku Lurie, tahun-tahun ini dapat kacau balau.
Cerna sapi
Matematikawan dianggap orang dengan pemikiran yang tidak ambigu: buktinya benar atau tidak; idenya bisa berhasil atau tidak. Namun, ahli matematika juga orang biasa, dan mereka bereaksi terhadap ide-ide baru dengan cara yang sama seperti orang biasa: secara subjektif, emosional, memiliki motif pribadi.
"Saya pikir banyak teks telah ditulis tentang ahli matematika dengan nada sedemikian rupa sehingga mereka mencari kebenaran yang sangat jelas," kata Campbell. "Tapi ini tidak terjadi." Mereka adalah orang-orang dengan selera mereka sendiri, zona nyaman, dan mereka dapat menyangkal hal-hal yang tidak mereka sukai karena alasan estetika atau pribadi. "
Dalam hal ini, pekerjaan Lurie telah menjadi tantangan yang kompleks bagi masyarakat. Sebenarnya, itu provokatif: inilah cara baru dan lebih baik untuk melakukan matematika. Pesan ini ditujukan terutama untuk ahli matematika, yang menghabiskan seluruh karir mereka mengembangkan metode yang Lurie unggul.
"Orang tidak selalu ingin melihat generasi berikutnya menulis ulang pekerjaan mereka, dan proses ini menciptakan ketegangan," kata Francis. "Ini adalah salah satu fitur dari teori kategori tak terbatas - sebagian besar karya sebelumnya bersesuaian."
Pekerjaan Lurie sulit dicerna karena alasan lain. Volume bahan berarti bahwa matematikawan harus menghabiskan bertahun-tahun membaca buku-bukunya. Hampir tidak mungkin untuk menuntut dari ahli matematika yang sibuk yang berada di tengah-tengah karir, dan bagi mahasiswa pascasarjana yang hanya memiliki beberapa tahun untuk memberikan hasil yang memungkinkan mereka untuk mencari pekerjaan, ini sangat berisiko.
Karya Lurie juga sangat abstrak, bahkan dibandingkan dengan sifat sangat abstrak dari semua studi matematika tingkat lanjut. Dan tidak semua orang menyukainya. "Banyak orang mengira pekerjaan Lurie adalah sampah abstrak, dan banyak yang jatuh cinta padanya," kata Campbell. "Ada beberapa opsi menengah, termasuk yang tidak mengerti sama sekali."
Gulungan EmilyKomunitas ilmiah terus-menerus merasakan ide-ide baru, tetapi biasanya ini terjadi secara perlahan dan dengan perasaan bahwa setiap orang bergerak pada saat yang sama. Munculnya ide-ide baru menciptakan kesulitan bagi aparat intelektual masyarakat. "Banyak hal baru muncul segera - ini seperti seekor boa yang mencoba mencerna seekor sapi," kata Campbell. "Massa besar melewati komunitas."
Jika Anda seorang ahli matematika yang percaya bahwa pendekatan Lurie adalah cara terbaik untuk melakukan matematika, maka jalan Anda ke depan akan kesepian. Hanya sedikit orang yang membaca karya Lurie, tidak ada buku teks untuk menceritakannya secara singkat, dan tidak ada seminar untuk membantu Anda mendapatkan perhatian Anda. "Hanya ada satu cara untuk mempelajari semua ini dengan sangat rinci - untuk duduk dan melakukan semuanya sendiri," kata Peter Heine, seorang mahasiswa pascasarjana di MIT yang menghabiskan satu tahun membaca karya Lurie. - Saya pikir ini yang paling sulit. “Tidak mudah untuk duduk, dan mencari tahu sendiri sendiri - yaitu, untuk duduk dan membaca 800 halaman Teori Topos Teori sendiri.
Seperti banyak penemuan baru, teori topos yang lebih tinggi membutuhkan ahli matematika untuk secara aktif berinteraksi dengan peralatan, yang memungkinkannya untuk bekerja. 16- , , . « , », — , , .
, . . : ?
"Ada situasi di mana karya tersebut kembali dari majalah dengan ulasan yang absurd, dari mana kurangnya pemahaman terlihat, atau butuh beberapa tahun untuk menerbitkannya," kata Barvik. "Ini bisa menjadi banyak ketidaknyamanan, karena karya yang tidak dipublikasikan yang telah ada di situs Anda selama bertahun-tahun terlihat semakin konyol."Namun, masalah terbesar bukanlah karya yang tidak dipublikasikan, tetapi bekerja menggunakan kategori tak terhingga, dan diterbitkan - tetapi mengandung kesalahan.. , . , – , , , - , .
« , —
, , . – , , , , – , , - , . , ».
. , , .
« », — .
Terlepas dari semua formalismenya, matematika seharusnya tidak menjadi teks suci yang hanya bisa dibaca oleh pendeta. Di area ini tidak hanya volume tebal diperlukan, tetapi juga buklet, tidak hanya wahyu awal, tetapi juga interpretasi deskripsi mereka. Sementara itu, teori kategori tak terbatas ada, sebagian besar, dalam bentuk beberapa buku besar di rak."Kamu bisa mengambil pendekatan. 'Yakub akan memberitahumu apa yang harus dilakukan, dan semuanya beres," kata Rezk. "Atau Anda dapat memutuskan bahwa 'Kami tidak tahu cara menyajikan topik kami dengan cukup baik sehingga orang dapat menggunakannya."Namun, beberapa matematikawan dapat menerima tantangan dan menjadikan kategori infinity sebagai teknologi yang dapat digunakan lebih banyak orang dari bidang studi mereka.Teori Ramah Pengguna
Untuk menerjemahkan kategori infinitas ke dalam objek yang mampu melakukan pekerjaan matematika nyata, Lurie harus membuktikan teorema yang terkait dengannya. Dan untuk ini, ia harus memilih lanskap yang akan dijadikan bukti ini - seperti halnya orang yang bergerak dalam bidang geometri, perlu untuk memilih sistem koordinat untuk bekerja. Matematikawan menyebut pemilihan model ini.Lurie mengembangkan kategori infinitas pada model quasicategories. Matematikawan lain sebelum dia mengembangkan kategori tak terbatas pada model lain. Dan meskipun pekerjaan mereka tidak selengkap pekerjaan Lurie, dalam beberapa situasi lebih mudah untuk berurusan dengan mereka. "Yakub memilih model dan memeriksa bahwa semuanya berfungsi di dalamnya, tetapi seringkali itu bukan yang termudah," kata Zakharevich.Dalam geometri, matematikawan memahami dengan jelas cara berpindah antara sistem koordinat yang berbeda. Mereka juga membuktikan bahwa teorema terbukti dalam beberapa kondisi berfungsi di orang lain.Untuk kategori tak terhingga, jaminan semacam itu tidak ada. Namun, ketika matematikawan menulis karya menggunakan kategori infinities, mereka sering dengan mudah beralih di antara model, menyarankan (tetapi tidak membuktikan) portabilitas hasil. "Orang-orang tidak merinci apa yang mereka lakukan, mereka beralih di antara semua model yang berbeda ini, dan mereka berkata: Ah, itu adalah hal yang sama," kata Heine. "Tapi itu bukan bukti."Selama enam tahun terakhir, beberapa ahli matematika telah mencoba untuk mendapatkan jaminan ini. Ryl dan Dominic Veritydari McUyra University di Australia, mengembangkan cara untuk menggambarkan kategori tak terhingga, mengatasi kesulitan yang muncul di platform sebelumnya menggunakan model-model tertentu. Pekerjaan mereka, berdasarkan karya-karya Barvik dan yang lain sebelumnya, membuktikan bahwa banyak teorema Teori Topos Tinggi tetap benar terlepas dari model yang digunakan. Dan mereka membuktikan kompatibilitas ini dengan cara yang tepat: "Kami mempelajari kategori-kategori ketidakterbatasan, objek-objeknya adalah kategori ketidakterbatasan," kata Ril. "Teori kategori menggigit ekornya.". , . , , , , , , , « ».
« , , — . – , ».
.
Kerodon, yang ia rencanakan berubah menjadi semacam buku referensi tentang teori kategori tertinggi, mirip dengan Wikipedia. Tiga belas tahun setelah Teori Topos meresmikan matematika kesetaraan, inisiatif ini mencoba untuk memperbaiki dan menyebarkan ide-ide ini - untuk membuat matematika kesetaraan lebih mudah diakses."Genius memiliki peran penting dalam pengembangan matematika, tetapi pengetahuan itu sendiri adalah hasil kerja seluruh komunitas," kata Zhoyal. "Tujuan sebenarnya dari pengetahuan adalah untuk menjadi pengetahuan seluruh komunitas, dan bukan untuk menjadi milik satu atau dua orang."