Dalam jejak
"Kemenangan kami: TopCoder Open 2019" Saya menerbitkan tugas dari jalur Algoritma
(pemrograman olahraga klasik. Dalam satu setengah jam, Anda perlu menyelesaikan tiga masalah di Jawa, C #, C ++ atau Python.)1. Pai untuk enam
Pernyataan masalahBatas waktu adalah 4 detik.
Anda punya kue. Dilihat dari atas, kue tersebut berbentuk poligon cembung (ketat). Anda diberi koordinat titik dalam bilangan bulat X dan Y.
Anda punya lima teman. Anda ingin membagi kue menjadi enam bagian dengan luas yang sama (tetapi tidak harus dengan bentuk yang sama). Tentu saja, siapa pun dapat melakukannya dalam lima potongan, tetapi hanya pro yang dapat melakukannya dalam tiga potongan.
Temukan tiga potongan garis lurus melalui satu titik yang akan membagi kue menjadi enam bagian yang berukuran sama. Cetak {x, y, d1, d2, d3}, di mana (x, y) adalah titik umum dari ketiga bagian, dan d1, d2, d3 adalah sudut arah dari bagian dalam radian.
DefinisiKelas: CakeForSix
Metode: potong
Parameter: int [], int []
Pengembalian: dua kali lipat []
Metode tanda tangan: gandakan [] potong (int [] x, int [] y)
(pastikan metode Anda bersifat publik)
Catatan- Arah positif sepanjang sumbu x adalah 0 (radian), arah positif sepanjang sumbu y adalah pi / 2 (radian).
- Pemotongan dalam arah d mirip dengan pemotongan dalam arah pi * k + d untuk bilangan bulat k.
- Anda dapat menampilkan arah apa pun, tidak harus dari [0, pi).
- Grader akan menghitung luas enam potong kue Anda menjadi dua kali lipat. Jawabannya akan diterima jika perbedaan relatif atau absolut di antara mereka kurang dari 10 ^ (- 4).
- Lebih tepatnya, biarkan X dan Y menjadi yang terkecil dan terbesar dari enam area Anda yang dihitung oleh grader. Maka jawaban Anda akan diterima jika Y <maks (X + 10 ^ (- 4), X * 1 + 10 ^ (- 4)))).
- (Dalam versi asli masalah, akurasi 1e-7 digunakan sebagai pengganti 1e-4. Untuk mengatasi masalah ini dalam arsip, batas akurasi berkurang karena adanya kasus panggilan yang kemungkinan besar membuat tugas tidak dapat diselesaikan dengan akurasi 1e-7. Di dunia yang ideal, pembatasan jangan biarkan kasus seperti itu dan masih membutuhkan akurasi tinggi, jadi menyelesaikan masalah dengan beberapa optimasi numerik umum tidak mudah.)
Keterbatasan- x mengandung mulai dari 3 hingga 50 elemen.
- y berisi elemen sebanyak x.
- semua koordinat antara 0 dan 10.000 inklusif
- x dan y mendefinisikan poligon cembung dalam arah berlawanan arah jarum jam.
Asli dalam bahasa InggrisPernyataan Masalah
Batas waktu adalah 4 detik.
Anda punya kue. Dilihat dari atas, kuenya adalah poligon cembung (ketat). Anda diberikan koordinat simpulnya di int [] sx dan y.
Anda punya lima teman. Anda sekarang ingin memotong kue menjadi enam bagian dengan luas yang sama (tetapi bentuknya tidak harus sama). Tentu saja, siapa pun dapat melakukannya dalam lima pemotongan - tetapi hanya seorang profesional sejati yang dapat melakukannya dalam tiga pemotongan!
Temukan tiga potongan garis lurus melewati titik yang sama yang memotong kue menjadi enam bagian yang sama besar. Kembali {x, y, d1, d2, d3}, di mana (x, y) adalah titik umum dari tiga potongan, dan d1, d2, d3 adalah arah mereka dalam radian.
Definisi
Kelas: CakeForSix
Metode: potong
Parameter: int [], int []
Pengembalian: dua kali lipat []
Metode tanda tangan: gandakan [] potong (int [] x, int [] y)
(pastikan metode Anda bersifat publik)
Catatan
- Arah positif sepanjang sumbu x adalah 0 (radian), arah positif sepanjang sumbu y adalah pi / 2 (radian).
- Pemotongan arah d sama dengan pemotongan pada arah pi * k + d untuk bilangan bulat k.
- Anda dapat mengembalikan arah apa pun, tidak harus dari [0, pi).
- Grader akan menghitung luas enam potong kue Anda menjadi dua kali lipat. Jawabannya akan diterima jika perbedaan relatif atau absolut di antara mereka kurang dari 10 ^ (- 4).
- Lebih tepatnya, biarkan X dan Y menjadi yang terkecil dan terbesar dari enam area Anda, seperti yang dihitung oleh grader. Kemudian, jawaban Anda akan diterima jika Y <maks (X + 10 ^ (- 4), X * (1 + 10 ^ (- 4)))).
- (Versi asli dari masalah menggunakan presisi 1e-7 dan bukan 1e-4. Untuk pemecahan masalah ini dalam arsip, batas presisi diturunkan karena adanya kasus tantangan yang kemungkinan besar membuat tugas tidak dapat diselesaikan dengan presisi 1e-7 Dalam dunia ideal kendala tidak akan memungkinkan kasus seperti itu dan masih membutuhkan presisi tinggi, sehingga tidak mudah untuk menyelesaikan masalah melalui beberapa optimasi numerik umum.)
Kendala
- x akan memiliki antara 3 dan 50 elemen, inklusif.
- y akan memiliki jumlah elemen yang sama dengan x.
- Semua koordinat antara 0 dan 10.000, inklusif.
- x dan y akan menjelaskan poligon cembung dalam urutan berlawanan arah jarum jam.
Contohnya
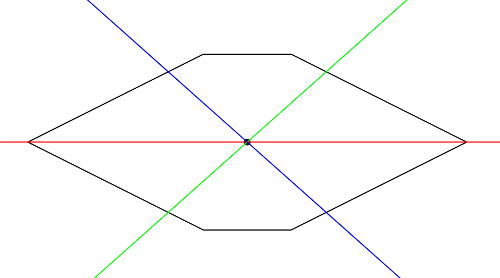
0){0, 20, 30, 50, 30, 20}
{10, 0, 0, 10, 20, 20}
Pengembalian:
{24.999999999437453, 9.999999999500002, 0,0, 0,7266423406817211, 2,4149503129080787}
Hexagon simetris tetapi tidak teratur. Contoh jawaban terkait dengan memotongnya menjadi dua secara horizontal dan membuat dua potongan lainnya di tengah, yang membagi setiap bagian menjadi tiga bagian.
 1)
1){0, 1000, 0}
{0, 0, 1000}
Pengembalian:
{333.3333333331763, 333.3333333332546, 0.7853981633986264, 2.0344439357948154, 2.6779450445891753}
Segitiga kanan Sekali lagi, kita bisa mulai dengan salah satu dari tiga potongan di sepanjang sumbu simetri.
 2)
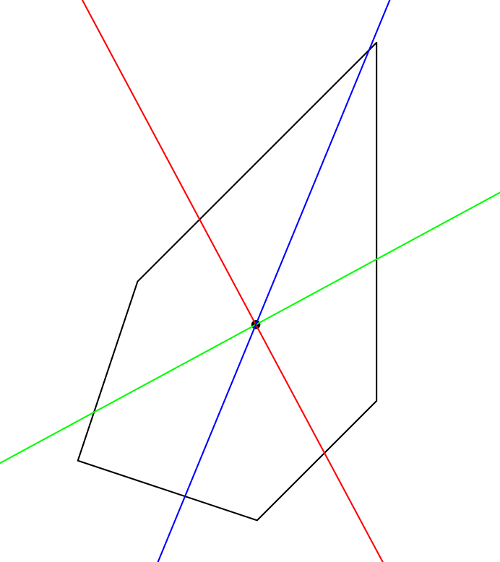
2){40, 70, 90, 90, 50}
{30, 20, 40, 100, 60}
Pengembalian:
{69.79517771922892, 52.77575974637605, 2.0616329654335885, 3.637826104091601, 4.32123485812475}
Pentagon salah.
 3)
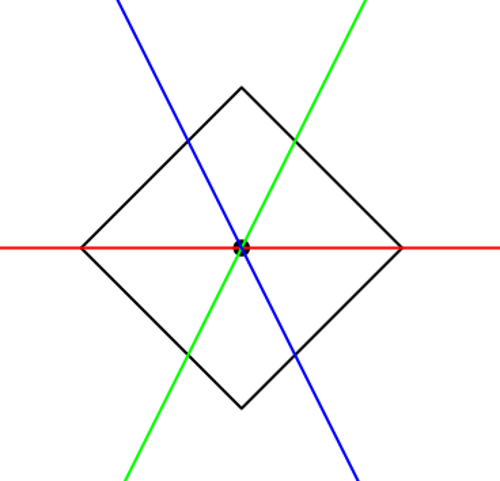
3){300, 400, 300, 200}
{500, 600, 700, 600}
Pengembalian: {299.99999999974995, 599.9999999995, 0.0, 1.107148717794088, 2.034443935795705}
Sebuah kotak diputar 45 derajat.
[
Sumber ]