Kuda itu bergerak sedikit. Bitboard Catur

Selamat siang Saya menulis artikel ini terutama untuk siswa dari kursus "Algoritma untuk Pengembang" di OTUS dan hari ini saya ingin membagikannya dengan semua pembaca blog kami.

Seekor kuda catur berdiri di atas papan catur dan menatap papan catur dengan serius.
Berapa banyak gerakan berbeda yang bisa dia lakukan?



Alhamdulillah bagi penemu catur, ada 64 sel di papan tulis.
Puji arsitek komputer - tipe ulong juga memiliki 64 bit.
Kebetulan ini harus terjadi!
Ide cemerlang menyarankan dirinya sendiri - untuk menyimpan seluruh papan dalam satu nomor penuh ! Bahkan ada istilah khusus untuk solusi ini - Bitboard - papan bit.

Jadi bagaimana cara cepat menemukan jumlah gerakan kuda catur menggunakan ide ini?

Diberikan: knightNr - nomor sel papan tempat kuda berada (dari 0 hingga 63).
Itu perlu: moveCount - jumlah bidang di mana ia bisa pergi (dari 2 hingga 8).

Algoritma

1. Konversikan nomor kandang kuda menjadi ulong - nilai papan bit
knightNr -> knightBits

2. Tetapkan bit untuk semua kemungkinan gerakan kuda
knightBits -> movesBits

3. Hitung jumlah bit unit
moveBits -> movesCount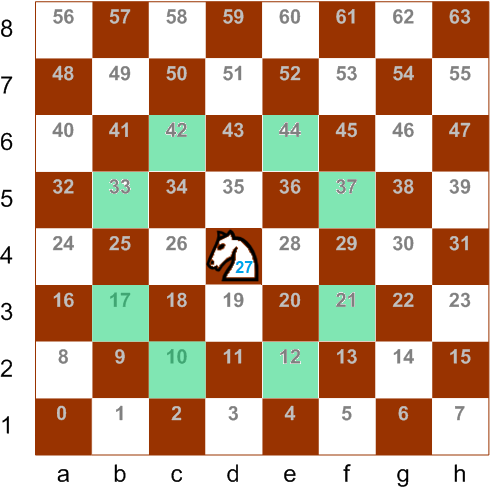



Langkah pertama sangat sederhana, Anda perlu menggeser bit nol ke kiri dengan jumlah posisi yang ditentukan.

ulong knightBits = 1 << knightNr; 

Langkah kedua sedikit lebih rumit. Seekor kuda dapat pergi ke 8 arah yang berbeda. Kami akan mempertimbangkan offset ini bukan "horizontal / vertikal", tetapi dengan posisi bit. Artinya, kami mempertimbangkan berapa banyak posisi yang Anda butuhkan untuk menggeser bit awal untuk setiap gerakan. Kemudian kita "menjumlahkan" semuanya dengan operasi logis "atau".

Mari kita mulai mendaftar gerakan dari sisi kiri papan ke kanan:

  movesBits = knightBits << 6 | knightBits >> 10 //  b5  b3 | knightBits << 15 | knightBits >> 17 //  c6  c2 | knightBits << 17 | knightBits >> 15 //  e6  e2 | knightBits << 10 | knightBits >> 6 //  f5  f3; 

Benar, keren!?

Sayangnya, ada "lubang hitam" di tepi papan. Misalnya, menurut algoritme ini, dari sel a4 (bit # 24) Anda bisa sampai ke sel g2 (bit # 14 = 24 - 10), lompatan ini adalah teleportasi dari kuda catur berbentuk bola dalam ruang hampa pada papan melalui lubang hitam ke vertikal ekstrem ...

Untuk mengecualikan lompatan kuantum kuda di tepi papan, perlu untuk "melepaskan" band-band ekstrim setelah bergerak. Misalnya, untuk bergerak +6 dan -10 (dua sel ke kiri), perlu untuk membatalkan nilai yang diperoleh pada g dan h vertikal, karena Anda tidak dapat berakhir pada vertikal ini setelah memindahkan "kiri" dua gerakan.

Untuk melakukan ini, kita memerlukan konstanta 4 bit grid, di mana semua bit diatur ke 1, kecuali untuk vertikal yang ditunjukkan. Yaitu:

  ulong nA = 0xFeFeFeFeFeFeFeFe; ulong nAB = 0xFcFcFcFcFcFcFcFc; ulong nH = 0x7f7f7f7f7f7f7f7f; ulong nGH = 0x3f3f3f3f3f3f3f3f; 

Di bagian atas dan bawah papan catur ada juga "lubang hitam" yang benar-benar menyerap kuda, sehingga mereka tidak perlu diperiksa secara terpisah.

Sekarang algoritma untuk menghasilkan gerakan kuda yang diizinkan terlihat seperti ini:

  movesBits = nGH & (knightBits << 6 | knightBits >> 10) | nH & (knightBits << 15 | knightBits >> 17) | nA & (knightBits << 17 | knightBits >> 15) | nAB & (knightBits << 10 | knightBits >> 6); 

Ini bekerja sangat (!) Cepat.

Beberapa kutu - dan kami memiliki bitmap dari semua kemungkinan petualangan kuda. Yang paling menakjubkan adalah bahwa algoritma ini berfungsi dengan baik walaupun ada beberapa kuda di papan. Dia sekaligus menghasilkan semua gerakan yang mungkin untuk semua kuda! Benar hebat!

Tetap menghitung jumlah bit

Cara termudah adalah dengan menggeser angka 1 bit ke kanan dan menghitung yang. Kesulitan - 64 operasi. Memori - 64 bit.

Cara tercepat adalah membuat cache / array dengan 65536 elemen, di mana jumlah bit untuk setiap indeks ditulis dari 0 hingga 65535. Dan tambahkan 4 elemen dari array ini yang sesuai dengan segmen 16-bit berikutnya dari angka tersebut.
Kesulitan - 4 operasi. Memori - 64 kilobyte.

Tetapi kami akan mempertimbangkan cara yang paling rumit , kompleksitasnya sama dengan jumlah bit tunggal dalam angka. Karena tidak banyak gerakan, pendekatan ini akan menjadi yang paling optimal bagi kami.

Untuk memulainya, kami mencatat bahwa dengan mengurangi satu unit dari angka, kami mengubah semua nol "benar" menjadi satuan, dan unit terluar menjadi nol:

 1001010100010000 - 1 = 1001010100001111 

Selanjutnya, terapkan operasi logis “dan” untuk angka-angka ini:

 1001010100010000 & 1001010100001111 = 1001010100000000 

Seperti yang Anda lihat, dengan cara yang rumit kami mereset unit paling kanan ke nol. Ulangi operasi ini sampai hasilnya nol. Berapa banyak iterasi, begitu banyak bit tunggal. Benar hebat!

Beginilah cara algoritma ini ditulis secara lengkap:

  int movesCount = 0; while (movesBits != 0) { movesBits &= (movesBits - 1); movesCount ++; } 

Masalahnya terpecahkan!

Tugas ini memiliki solusi lain, sangat sederhana, murni logis: untuk menentukan jarak ksatria dari tepi papan catur (di sudut ada 2 gerakan, di bagian tepi ada 3 hingga 6 gerakan, di tengah ada 8 gerakan). Tetapi jika kita harus memecahkan masalah "head on" dengan cara ini, kita tidak akan tahu tentang papan bit, tentang topeng bit vertikal, tentang algoritma untuk dengan cepat menghitung bit tunggal dan tentang lubang hitam untuk kuda bola dalam ruang hampa ...

Sekarang kita tahu semua tentang itu. Kehidupan programmer catur menjadi lebih kaya dan lebih bermakna, tepuk tangan!

Kerjakan sendiri: lakukan hal yang sama untuk Raja Catur.