Geekly articles weekly

Optimalisasi Strategi Monte Carlo Blackjack

Terjemahan artikel disiapkan khusus untuk siswa kursus Pembelajaran Mesin .



Pelatihan yang diperkuat mengambil dunia Kecerdasan Buatan. Mulai dari AlphaGo dan AlphaStar , semakin banyak kegiatan yang sebelumnya didominasi oleh manusia sekarang ditaklukkan oleh agen AI berdasarkan pelatihan penguatan. Singkatnya, pencapaian ini bergantung pada pengoptimalan tindakan agen dalam lingkungan tertentu untuk mencapai hadiah maksimum. Dalam beberapa artikel terakhir dari GradientCrescent, kami telah melihat berbagai aspek mendasar dari pembelajaran yang diperkuat, dari dasar-dasar sistem bandit dan pendekatan berbasis kebijakan hingga mengoptimalkan perilaku berbasis imbalan di lingkungan Markov . Semua pendekatan ini membutuhkan pengetahuan lengkap tentang lingkungan kita. Pemrograman dinamis , misalnya, mengharuskan kita memiliki distribusi probabilitas lengkap dari semua transisi keadaan yang mungkin. Namun, pada kenyataannya, kami menemukan bahwa sebagian besar sistem tidak dapat sepenuhnya ditafsirkan, dan bahwa distribusi probabilitas tidak dapat diperoleh secara eksplisit karena kompleksitas, ketidakpastian yang melekat, atau keterbatasan dalam kemampuan komputasi. Sebagai analogi, pertimbangkan tugas ahli meteorologi - jumlah faktor yang terlibat dalam peramalan cuaca bisa sangat besar sehingga tidak mungkin untuk secara akurat menghitung probabilitas.

Untuk kasus seperti itu, metode pengajaran seperti Monte Carlo adalah solusinya. Istilah Monte Carlo umumnya digunakan untuk menggambarkan pendekatan apa pun terhadap estimasi pengambilan sampel acak. Dengan kata lain, kita tidak memprediksikan pengetahuan tentang lingkungan kita, tetapi belajar dari pengalaman dengan melalui urutan negara contoh, tindakan dan penghargaan yang diperoleh sebagai hasil interaksi dengan lingkungan. Metode-metode ini bekerja dengan mengamati secara langsung hadiah yang dikembalikan oleh model selama operasi normal untuk menilai nilai rata-rata dari kondisinya. Menariknya, bahkan tanpa pengetahuan tentang dinamika lingkungan (yang harus dianggap sebagai distribusi probabilitas transisi negara), kita masih bisa mendapatkan perilaku optimal untuk memaksimalkan imbalan.

Sebagai contoh, perhatikan hasil lemparan 12 dadu. Mempertimbangkan lemparan ini sebagai satu negara, kita dapat merata-rata hasil ini untuk lebih dekat dengan hasil prediksi yang sebenarnya. Semakin besar sampel, semakin akurat kita akan mendekati hasil yang diharapkan.


Jumlah rata-rata yang diharapkan pada 12 dadu untuk 60 tembakan adalah 41,57

Jenis penilaian berbasis pengambilan sampel ini mungkin tampak akrab bagi pembaca, karena pengambilan sampel seperti itu juga dilakukan untuk sistem k-bandit. Alih-alih membandingkan bandit yang berbeda, metode Monte Carlo digunakan untuk membandingkan kebijakan yang berbeda di lingkungan Markov, menentukan nilai negara sebagai kebijakan tertentu diikuti sampai pekerjaan selesai.

Estimasi nilai Monte Carlo


Dalam konteks pembelajaran penguatan, metode Monte Carlo adalah cara untuk mengevaluasi signifikansi keadaan model dengan rata-rata hasil sampel. Karena kebutuhan untuk keadaan terminal, metode Monte Carlo secara inheren berlaku untuk lingkungan episodik. Karena keterbatasan ini, metode Monte Carlo biasanya dianggap "otonom" di mana semua pembaruan dilakukan setelah mencapai keadaan terminal. Analogi sederhana dengan menemukan jalan keluar dari labirin dapat diberikan - pendekatan otonom akan memaksa agen untuk mencapai akhir sebelum menggunakan pengalaman perantara yang diperoleh untuk mencoba mengurangi waktu yang dibutuhkan untuk melewati labirin. Di sisi lain, dengan pendekatan online, agen akan terus mengubah perilakunya selama lorong labirin, mungkin dia akan melihat bahwa koridor hijau mengarah ke jalan buntu dan memutuskan untuk menghindarinya, misalnya. Kami akan membahas pendekatan online di salah satu artikel berikut.

Metode Monte Carlo dapat dirumuskan sebagai berikut:



Untuk lebih memahami bagaimana metode Monte Carlo bekerja, pertimbangkan diagram transisi status di bawah ini. Hadiah untuk setiap transisi negara ditampilkan dalam warna hitam, faktor diskon 0,5 diterapkan untuk itu. Mari kita kesampingkan nilai aktual negara dan fokus pada menghitung hasil satu lemparan.


Diagram transisi keadaan. Nomor status ditampilkan dalam warna merah, hasilnya hitam.
Mengingat bahwa keadaan terminal mengembalikan hasil yang sama dengan 0, mari kita menghitung hasil dari setiap keadaan, dimulai dengan keadaan terminal (G5). Harap dicatat bahwa kami telah menetapkan faktor diskon ke 0,5, yang akan mengarah pada pembobotan terhadap status selanjutnya.



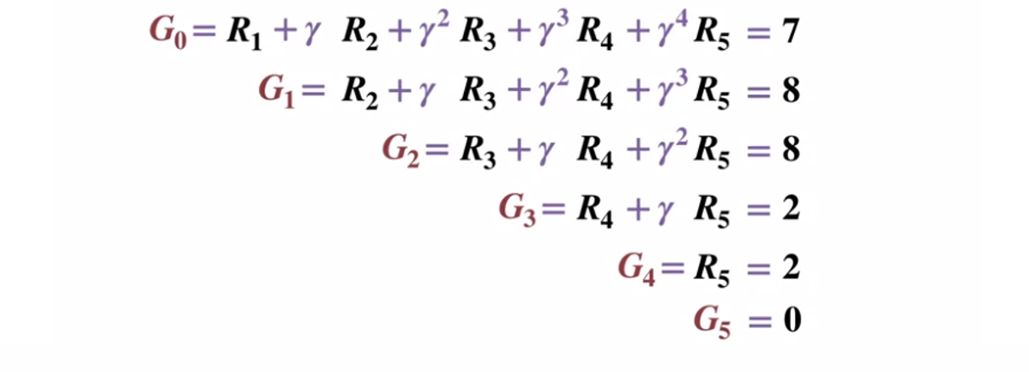
Atau lebih umum:



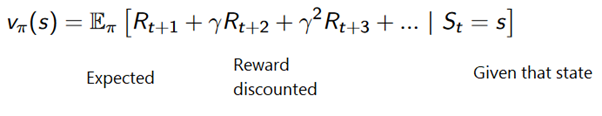
Untuk menghindari menyimpan semua hasil dalam daftar, kita dapat melakukan prosedur memperbarui nilai keadaan dalam metode Monte Carlo secara bertahap, menggunakan persamaan yang memiliki beberapa kesamaan dengan penurunan gradien tradisional:


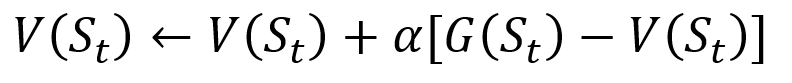Prosedur pembaruan bertahap Monte Carlo. S adalah status, V adalah nilainya, G adalah hasilnya, dan A adalah parameter nilai langkah.

Sebagai bagian dari pelatihan penguatan, metode Monte Carlo bahkan dapat diklasifikasikan sebagai Kunjungan Pertama atau Setiap Kunjungan. Singkatnya, perbedaan antara keduanya adalah berapa kali suatu negara bagian dapat dikunjungi sebelum pembaruan Monte Carlo. Metode Kunjungan Pertama Monte Carlo memperkirakan nilai semua negara bagian sebagai nilai rata-rata hasil setelah kunjungan tunggal ke masing-masing negara bagian sebelum penyelesaian, sedangkan metode setiap kunjungan Monte Carlo rata-rata hasil setelah n kunjungan sampai selesai. Kami akan menggunakan Kunjungan Pertama Monte Carlo di seluruh artikel ini karena kesederhanaannya.

Manajemen Kebijakan Monte Carlo


Jika model tidak dapat menyediakan kebijakan, Monte Carlo dapat digunakan untuk mengevaluasi nilai tindakan negara. Ini lebih berguna daripada sekadar makna negara, karena gagasan makna setiap tindakan (q) dalam keadaan tertentu memungkinkan agen untuk secara otomatis merumuskan kebijakan dari pengamatan di lingkungan yang tidak dikenal.

Secara lebih formal, kita dapat menggunakan Monte Carlo untuk memperkirakan q (s, a, pi) , hasil yang diharapkan ketika mulai dari negara, tindakan a, dan kebijakan selanjutnya Pi . Metode Monte Carlo tetap sama, kecuali bahwa ada dimensi tindakan tambahan yang diambil untuk keadaan tertentu. Dipercayai bahwa tindakan negara (s, a) berpasangan dikunjungi selama bagian ini jika keadaan pernah dikunjungi dan tindakan a dilakukan di dalamnya. Demikian pula, evaluasi tindakan nilai dapat dilakukan dengan menggunakan pendekatan "Kunjungan Pertama" dan "Setiap kunjungan".

Seperti dalam pemrograman dinamis, kita dapat menggunakan kebijakan iterasi umum (GPI) untuk membentuk kebijakan dari mengamati nilai tindakan negara.



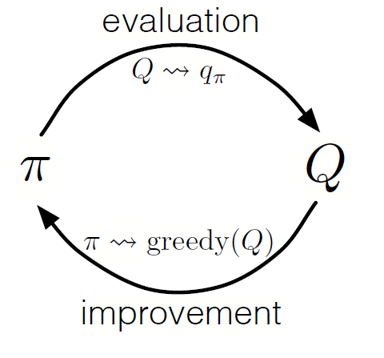
Dengan bergantian langkah-langkah evaluasi kebijakan dan peningkatan kebijakan, dan termasuk penelitian untuk memastikan bahwa semua tindakan yang mungkin dikunjungi, kita dapat mencapai kebijakan optimal untuk setiap kondisi. Untuk GPI Monte Carlo, rotasi ini biasanya dilakukan setelah akhir setiap pass.


GPI Monte Carlo

Strategi blackjack


Untuk lebih memahami bagaimana metode Monte Carlo bekerja dalam praktik dalam tugas menilai berbagai nilai negara, mari kita lakukan demonstrasi langkah demi langkah dari contoh permainan blackjack. Untuk memulai, mari kita tentukan aturan dan ketentuan permainan kami:

  • Kami akan bermain hanya melawan dealer, tidak akan ada pemain lain. Ini akan memungkinkan kami untuk mempertimbangkan tangan dealer sebagai bagian dari lingkungan.
  • Nilai kartu dengan angka sama dengan nilai nominal. Nilai kartu gambar: Jack, King and Queen adalah 10. Nilai kartu as dapat 1 atau 11 tergantung pada pilihan pemain.
  • Kedua belah pihak menerima dua kartu. Dua kartu pemain menghadap ke atas, salah satu kartu dealer juga menghadap ke atas.
  • Tujuan permainan adalah bahwa jumlah kartu yang ada adalah <= 21. Nilai lebih besar dari 21 adalah angka, jika kedua belah pihak memiliki nilai 21, maka permainan dimainkan secara seri.
  • Setelah pemain melihat kartunya dan kartu dealer pertama, pemain dapat memilih untuk membawanya kartu baru ("belum") atau tidak ("cukup") sampai ia puas dengan jumlah nilai kartu di tangannya.
  • Kemudian dealer menunjukkan kartu keduanya - jika jumlah yang dihasilkan kurang dari 17, ia wajib mengambil kartu hingga mencapai 17 poin, setelah itu ia tidak mengambil kartu lagi.

Mari kita lihat bagaimana metode Monte Carlo bekerja dengan aturan-aturan ini.

Babak 1.


Anda mendapatkan total 19. Tetapi Anda mencoba untuk menangkap keberuntungan dengan ekor, ambil kesempatan, dapatkan 3 dan bangkrut. Ketika Anda bangkrut, dealer hanya memiliki satu kartu terbuka dengan jumlah 10. Ini dapat direpresentasikan sebagai berikut:



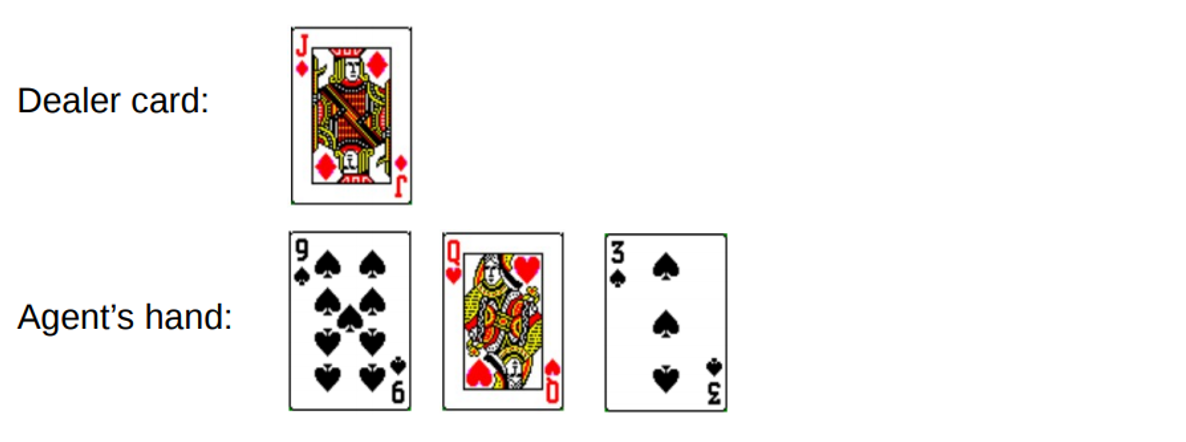
Jika kami bangkrut, hadiah kami untuk putaran adalah -1. Mari kita tetapkan nilai ini sebagai hasil pengembalian dari kondisi kedua dari belakang, menggunakan format berikut [Jumlah agen, jumlah dealer, kartu as?]:



Nah, sekarang kita kurang beruntung. Mari kita beralih ke babak lain.

Babak 2


Anda mengetik total 19. Kali ini Anda memutuskan untuk berhenti. Dealer memanggil 13, mengambil kartu dan bangkrut. Kondisi kedua dari belakang dapat dijelaskan sebagai berikut.



Mari kita jelaskan kondisi dan penghargaan yang kami terima di babak ini:



Dengan akhir bagian ini, kita sekarang dapat memperbarui nilai semua negara bagian kita di babak ini menggunakan hasil yang dihitung. Mengambil faktor diskon 1, kami hanya menyebarkan hadiah tangan baru kami, seperti yang dilakukan dengan transisi negara sebelumnya. Karena negara V (19, 10, tidak) sebelumnya dikembalikan -1, kami menghitung nilai pengembalian yang diharapkan dan menugaskannya ke negara kami:


Nilai status final untuk demonstrasi menggunakan blackjack sebagai contoh .

Implementasi


Mari kita menulis permainan blackjack menggunakan metode Monte Carlo kunjungan pertama untuk mengetahui semua nilai status yang mungkin (atau berbagai kombinasi di tangan) dalam permainan menggunakan Python. Pendekatan kami akan didasarkan pada pendekatan Sudharsan et. al. . Seperti biasa, Anda dapat menemukan semua kode dari artikel di GitHub kami .

Untuk mempermudah implementasi, kami akan menggunakan gym dari OpenAI. Pikirkan lingkungan sebagai antarmuka untuk memulai blackjack dengan jumlah kode minimal, ini akan memungkinkan kita untuk fokus pada penerapan pembelajaran yang diperkuat. Mudahnya, semua informasi yang dikumpulkan tentang status, tindakan, dan hadiah disimpan dalam variabel "observasi" , yang diakumulasikan selama sesi permainan saat ini.

Mari kita mulai dengan mengimpor semua perpustakaan yang kita butuhkan untuk mendapatkan dan mengumpulkan hasil kita.

import gym import numpy as np from matplotlib import pyplot import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from collections import defaultdict from functools import partial %matplotlib inline plt.style.use('ggplot')

Selanjutnya, mari kita inisialisasi lingkungan gym kita dan menetapkan kebijakan yang akan mengoordinasikan tindakan agen kami. Bahkan, kami akan terus mengambil kartu sampai jumlah di tangan mencapai 19 atau lebih, setelah itu kami berhenti.

 #Observation here encompassess all data about state that we need, as well as reactions to it env = gym.make('Blackjack-v0') #Define a policy where we hit until we reach 19. # actions here are 0-stand, 1-hit def sample_policy(observation): score, dealer_score, usable_ace = observation return 0 if score >= 19 else 1

Mari kita tentukan metode untuk menghasilkan data pass menggunakan kebijakan kami. Kami akan menyimpan informasi tentang status, tindakan yang diambil, dan remunerasi untuk tindakan tersebut.

 def generate_episode(policy, env): # we initialize the list for storing states, actions, and rewards states, actions, rewards = [], [], [] # Initialize the gym environment observation = env.reset() while True: # append the states to the states list states.append(observation) # now, we select an action using our sample_policy function and append the action to actions list action = sample_policy(observation) actions.append(action) # We perform the action in the environment according to our sample_policy, move to the next state observation, reward, done, info = env.step(action) rewards.append(reward) # Break if the state is a terminal state (ie done) if done: break return states, actions, rewards

Akhirnya, mari kita mendefinisikan kunjungan pertama fungsi prediksi Monte Carlo. Pertama, kami menginisialisasi kamus kosong untuk menyimpan nilai status saat ini dan kamus yang menyimpan jumlah catatan untuk setiap negara bagian dalam lintasan yang berbeda.

 def first_visit_mc_prediction(policy, env, n_episodes): # First, we initialize the empty value table as a dictionary for storing the values of each state value_table = defaultdict(float) N = defaultdict(int)

Untuk setiap pass, kami memanggil metode generate_episode kami untuk mendapatkan informasi tentang nilai-nilai status dan hadiah yang diterima setelah keadaan terjadi. Kami juga menginisialisasi variabel untuk menyimpan hasil tambahan kami. Kemudian kami mendapatkan hadiah dan nilai status saat ini untuk setiap negara yang dikunjungi selama pass, dan meningkatkan pengembalian variabel kami dengan nilai hadiah per langkah.

 for _ in range(n_episodes): # Next, we generate the epsiode and store the states and rewards states, _, rewards = generate_episode(policy, env) returns = 0 # Then for each step, we store the rewards to a variable R and states to S, and we calculate for t in range(len(states) — 1, -1, -1): R = rewards[t] S = states[t] returns += R # Now to perform first visit MC, we check if the episode is visited for the first time, if yes, #This is the standard Monte Carlo Incremental equation. # NewEstimate = OldEstimate+StepSize(Target-OldEstimate) if S not in states[:t]: N[S] += 1 value_table[S] += (returns — value_table[S]) / N[S] return value_table

Biarkan saya mengingatkan Anda bahwa karena kami menerapkan kunjungan pertama Monte Carlo, kami mengunjungi satu negara bagian dalam satu pass. Oleh karena itu, kami melakukan pemeriksaan bersyarat pada kamus negara bagian untuk melihat apakah negara tersebut telah dikunjungi. Jika kondisi ini terpenuhi, kami dapat menghitung nilai baru menggunakan prosedur yang didefinisikan sebelumnya untuk memperbarui nilai keadaan menggunakan metode Monte Carlo dan meningkatkan jumlah pengamatan untuk keadaan ini dengan 1. Kemudian kami mengulangi proses untuk lulus berikutnya untuk akhirnya mendapatkan nilai rata-rata dari hasil .

Ayo jalankan apa yang kita dapatkan dan lihat hasilnya!

 value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000) for i in range(10): print(value.popitem())


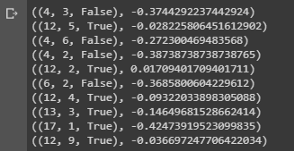Kesimpulan sampel yang menunjukkan nilai keadaan berbagai kombinasi di tangan dalam blackjack.

Kami dapat terus melakukan pengamatan Monte Carlo untuk 5000 lintasan dan membangun distribusi nilai-nilai negara yang menggambarkan nilai-nilai kombinasi apa pun di tangan pemain dan dealer.

 def plot_blackjack(V, ax1, ax2): player_sum = np.arange(12, 21 + 1) dealer_show = np.arange(1, 10 + 1) usable_ace = np.array([False, True]) state_values = np.zeros((len(player_sum), len(dealer_show), len(usable_ace))) for i, player in enumerate(player_sum): for j, dealer in enumerate(dealer_show): for k, ace in enumerate(usable_ace): state_values[i, j, k] = V[player, dealer, ace] X, Y = np.meshgrid(player_sum, dealer_show) ax1.plot_wireframe(X, Y, state_values[:, :, 0]) ax2.plot_wireframe(X, Y, state_values[:, :, 1]) for ax in ax1, ax2: ax.set_zlim(-1, 1) ax.set_ylabel('player sum') ax.set_xlabel('dealer sum') ax.set_zlabel('state-value') fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8),subplot_kw={'projection': '3d'}) axes[0].set_title('state-value distribution w/o usable ace') axes[1].set_title('state-value distribution w/ usable ace') plot_blackjack(value, axes[0], axes[1])


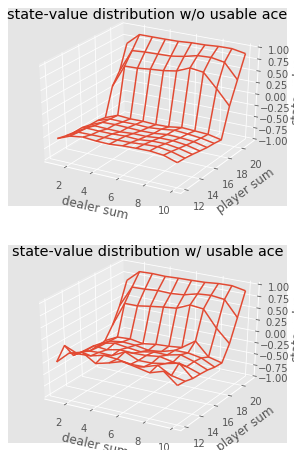Visualisasi nilai keadaan berbagai kombinasi di blackjack.

Jadi, mari kita simpulkan apa yang kita pelajari.

  • Metode pembelajaran berbasis sampel memungkinkan kita untuk mengevaluasi nilai keadaan dan kondisi tindakan tanpa dinamika transisi, hanya dengan pengambilan sampel.
  • Pendekatan Monte Carlo didasarkan pada pengambilan sampel acak model, mengamati imbalan yang dikembalikan oleh model, dan mengumpulkan informasi selama operasi normal untuk menentukan nilai rata-rata negara bagian.
  • Menggunakan metode Monte Carlo, kebijakan iterasi umum mungkin.
  • Nilai semua kemungkinan kombinasi di tangan pemain dan dealer di blackjack dapat diperkirakan menggunakan beberapa simulasi Monte Carlo, membuka jalan bagi strategi yang dioptimalkan.

Ini menyimpulkan pengantar metode Monte Carlo. Dalam artikel kami berikutnya, kami akan beralih ke metode pengajaran bentuk pembelajaran Perbedaan Temporal.

Sumber:


Sutton et. al, Pembelajaran Penguatan
White et. al, Fundamentals of Reinforcement Learning, University of Alberta
Silva et. al, Pembelajaran Penguatan, UCL
Platt et. Al, Universitas Northeaster

Itu saja. Sampai jumpa di lapangan !

Source: https://habr.com/ru/post/id477042/

More articles:


All Articles