Mengoptimalkan kompiler adalah dasar dari perangkat lunak modern: mereka memungkinkan pemrogram untuk menulis kode dalam bahasa yang mereka pahami, kemudian mengubahnya menjadi kode yang dapat dieksekusi secara efisien oleh peralatan. Tugas mengoptimalkan kompiler adalah untuk memahami apa program input yang Anda lakukan dan membuat program output yang melakukan hal yang sama, hanya lebih cepat.
Pada artikel ini, kita akan melihat beberapa teknik inferensi dasar dalam mengoptimalkan kompiler: bagaimana merancang program yang dengannya kompiler dapat bekerja dengan mudah; pengurangan apa yang dapat dilakukan dalam program Anda dan bagaimana menggunakannya untuk mengurangi dan mempercepatnya.
Pengoptimal program dapat dijalankan di mana saja: sebagai langkah dalam proses kompilasi yang besar (
Scala Optimizer ); sebagai program terpisah, diluncurkan setelah kompiler dan sebelum eksekusi (
Proguard ); atau sebagai bagian dari lingkungan runtime yang mengoptimalkan program selama pelaksanaannya (
JVM JIT compiler ). Keterbatasan dalam SEO bervariasi tergantung pada situasi, tapi masalahnya adalah sama: untuk mengambil program sumber dan mengubah output, yang melakukan hal yang sama, tapi lebih cepat.
Pertama, kita akan melihat beberapa contoh optimisasi rancangan program, sehingga Anda memahami apa yang biasanya dilakukan pengoptimal dan bagaimana melakukannya secara manual. Kemudian kami akan mempertimbangkan beberapa cara untuk mempresentasikan program, dan akhirnya kami akan menganalisis algoritma dan teknik yang dengannya Anda dapat menganalisis program dan kemudian membuatnya lebih kecil dan lebih cepat.
Program konsep
Semua contoh akan diberikan di Jawa. Bahasa ini sangat umum dan dikompilasi menjadi assembler yang relatif sederhana -
Java Bytecode . Jadi kami akan membuat fondasi yang baik, berkat itu kami dapat menjelajahi teknik optimisasi kompilasi menggunakan contoh nyata yang dapat dieksekusi. Semua teknik yang dijelaskan di bawah ini berlaku di hampir semua bahasa pemrograman lainnya.
Pertama, pertimbangkan konsep program. Ini berisi berbagai logika, mendaftarkan hasil standar di dalam proses dan mengembalikan hasil yang dihitung. Program itu sendiri tidak masuk akal, tetapi akan digunakan sebagai ilustrasi tentang apa yang dapat dioptimalkan sambil mempertahankan perilaku yang ada:
static int main(int n){ int count = 0, total = 0, multiplied = 0; Logger logger = new PrintLogger(); while(count < n){ count += 1; multiplied *= count; if (multiplied < 100) logger.log(count); total += ackermann(2, 2); total += ackermann(multiplied, n); int d1 = ackermann(n, 1); total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
Untuk saat ini, kami menganggap bahwa program ini adalah semua yang kami miliki, tidak ada bagian lain dari kode yang menyebutnya. Itu hanya memasukkan data ke
main , mengeksekusi, dan mengembalikan hasilnya. Sekarang mari kita optimalkan program ini.
Contoh Pengoptimalan
Pemain dan inlining
Anda mungkin telah memperhatikan bahwa variabel
logger memiliki tipe yang tidak akurat: terlepas dari label
Logger , berdasarkan kode, kita dapat menyimpulkan bahwa ini adalah subkelas khusus -
PrintLogger :
- Logger logger = new PrintLogger(); + PrintLogger logger = new PrintLogger();
Sekarang kita tahu bahwa
logger adalah
PrintLogger , dan kita tahu bahwa memanggil
logger.log dapat memiliki implementasi tunggal. Anda dapat sebaris:
- if (multiplied < 100) logger.logcount(); + if (multiplied < 100) System.out.println(count);
Ini akan mengurangi program dengan menghapus kelas
ErrLogger tidak perlu yang tidak digunakan, serta dengan menghapus berbagai metode
log public Logger , karena kami sebariskan ke satu tempat panggilan.
konstanta koagulasi
Selama eksekusi program,
count dan
total perubahan, tetapi
multiplied tidak: itu dimulai pada
0 dan dikalikan setiap kali melalui
multiplied = multiplied * count , tetap sama dengan
0 . Jadi, Anda bisa menggantinya di seluruh program dengan
0 :
static int main(int n){ - int count = 0, total = 0, multiplied = 0; + int count = 0, total = 0; PrintLogger logger = new PrintLogger(); while(count < n){ count += 1; - multiplied *= count; - if (multiplied < 100) System.out.println(count); + if (0 < 100) logger.log(count); total += ackermann(2, 2); - total += ackermann(multiplied, n); + total += ackermann(0, n); int d1 = ackermann(n, 1); - total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
Akibatnya, kita melihat bahwa
d1 * multiplied selalu
0 , yang berarti
total += d1 * multiplied tidak melakukan apa-apa dan dapat dihapus:
- total += d1 * multiplied
Penghapusan Kode Mati
Setelah
multiplied dan menyadari bahwa
total += d1 * multiplied tidak melakukan apa-apa, Anda dapat menghapus definisi
int d1 :
- int d1 = ackermann(n, 1);
Ini bukan lagi bagian dari program, dan karena
ackermann adalah fungsi murni, menghapus instalan tidak akan mempengaruhi hasil program.
Demikian pula, setelah inlining
logger.log sendiri
logger tidak lagi digunakan dan dapat dihapus:
- PrintLogger logger = new PrintLogger();
Pemindahan Cabang
Sekarang transisi kondisional pertama dalam siklus kita tergantung pada
0 < 100 . Karena ini selalu benar, Anda dapat menghapus kondisinya:
- if (0 < 100) System.out.println(count); + System.out.println(count);
Transisi bersyarat apa pun yang selalu benar dapat sejalan dengan tubuh kondisi, dan untuk transisi yang selalu salah, Anda dapat menghapus kondisi bersama tubuhnya.
Perhitungan sebagian
Sekarang kami menganalisis tiga panggilan yang tersisa ke
ackermann :
total += ackermann(2, 2); total += ackermann(0, n); int d2 = ackermann(n, count);
- Yang pertama memiliki dua argumen konstan. Fungsi murni, dan sementara menghitung
ackermann(2, 2) harus sama dengan 7. - Panggilan kedua memiliki satu argumen konstan
0 dan satu tidak diketahui n . Anda dapat meneruskannya ke definisi ackermann , dan ternyata ketika m adalah 0 , fungsi selalu mengembalikan n + 1.
- Dalam panggilan ketiga, kedua argumen tidak diketahui:
n dan count . Mari kita biarkan mereka di tempat untuk saat ini.
Mengingat bahwa banding ke
ackermann didefinisikan sebagai berikut:
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Anda dapat menyederhanakannya untuk:
- total += ackermann(2, 2); + total += 7 - total += ackermann(0, n); + total += n + 1 int d2 = ackermann(n, count);
akhir pengiriman
Definisi
d2 hanya digunakan dalam
if (count % 2 == 0) kondisional
if (count % 2 == 0) . Karena perhitungan
ackermann bersih, Anda dapat mentransfer panggilan ini ke
ackermann kondisional sehingga tidak diproses sampai digunakan:
- int d2 = ackermann(n, count); - if (count % 2 == 0) total += d2; + if (count % 2 == 0) { + int d2 = ackermann(n, count); + total += d2; + }
Ini akan menghindari setengah panggilan ke
ackermann(n, count) , mempercepat eksekusi program.
Sebagai perbandingan, fungsi
System.out.println tidak bersih, yang berarti tidak dapat ditransfer di dalam atau di luar lompatan bersyarat tanpa mengubah semantik program.
Hasil yang Dioptimalkan
Setelah mengumpulkan semua optimasi, kami mendapatkan kode sumber berikut:
static int main(int n){ int count = 0, total = 0; while(count < n){ count += 1; System.out.println(count); total += 7; total += n + 1; if (count % 2 == 0) { total += d2; int d2 = ackermann(n, count); } } return total; } static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Meskipun kami telah dioptimalkan secara manual, semua ini dapat dilakukan secara otomatis. Berikut ini adalah hasil dekompilasi pengoptimal prototipe yang saya tulis untuk program JVM:
static int main(int var0) { new Demo.PrintLogger(); int var1 = 0; int var3; for(int var2 = 0; var2 < var0; var2 = var3) { System.out.println(var3 = 1 + var2); int var10000 = var3 % 2; int var7 = var1 + 7 + var0 + 1; var1 = var10000 == 0 ? var7 + ackermann(var0, var3) : var7; } return var1; } static int ackermann__I__TI1__I(int var0) { if (var0 == 0) return 2; else return ackermann(var0 - 1, var0 == 0 ? 1 : ackermann__I__TI1__I(var0 - 1);); } static int ackermann(int var0, int var1) { if (var0 == 0) return var1 + 1; else return var1 == 0 ? ackermann__I__TI1__I(var0 - 1) : ackermann(var0 - 1, ackermann(var0, var1 - 1)); } static class PrintLogger implements Demo.Logger {} interface Logger {}
Kode yang didekompilasi sedikit berbeda dari versi yang dioptimalkan secara manual. Sesuatu yang tidak dapat dioptimalkan oleh kompiler (misalnya, panggilan yang tidak digunakan untuk
new PrintLogger ), tetapi sesuatu dilakukan dengan sedikit berbeda (misalnya,
ackermann dan
ackermann__I__TI1__I ). Tetapi untuk sisanya, pengoptimal otomatis melakukan hal yang sama seperti yang saya lakukan, menggunakan logika yang tertanam di dalamnya.
Muncul pertanyaan: bagaimana?
Tampilan menengah
Jika Anda mencoba membuat pengoptimal Anda sendiri, pertanyaan pertama yang muncul mungkin yang paling penting: apa itu "program"?
Tidak diragukan lagi, Anda terbiasa menulis dan mengubah program dalam bentuk kode sumber. Anda pasti mengeksekusi mereka dalam bentuk binari yang dikompilasi, bahkan mungkin men-debug binari. Anda mungkin menemukan program dalam bentuk
pohon sintaksis ,
kode tiga-alamat ,
A-Normal ,
Gaya Berlanjut Kelanjutan, atau
Penugasan Statis Tunggal .
Ada seluruh kebun binatang dari berbagai representasi program. Di sini kita akan membahas cara paling penting untuk mewakili "program" di dalam optimizer.
Kode sumber
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Kode sumber yang tidak dikompilasi juga merupakan representasi dari program Anda. Ini relatif kompak, dapat dibaca manusia, tetapi memiliki dua kelemahan:
- Kode sumber berisi semua detail nama dan pemformatan, yang penting bagi programmer, tetapi tidak berguna untuk komputer.
- Ada banyak program yang lebih keliru dalam bentuk kode sumber daripada yang benar, dan selama optimasi, Anda perlu memastikan bahwa program Anda dikonversi dari kode sumber input yang benar ke kode sumber keluaran yang benar.
Faktor-faktor ini menyulitkan pengoptimal untuk bekerja dengan program dalam bentuk kode sumber. Ya, Anda
dapat mengonversi program seperti itu, misalnya, menggunakan
ekspresi reguler untuk mengidentifikasi dan mengganti pola. Namun, yang pertama dari dua faktor membuatnya sulit untuk mengidentifikasi dengan andal pola dengan banyak detail asing. Dan faktor kedua sangat meningkatkan kemungkinan menjadi bingung dan mendapatkan program yang salah.
Pembatasan ini dapat diterima untuk konverter program yang dijalankan di bawah pengawasan manusia, misalnya, ketika Anda dapat menggunakan
Codemod untuk
memperbaiki dan mengubah basis kode. Namun, Anda tidak dapat menggunakan kode sumber sebagai model utama pengoptimal otomatis.
Pohon sintaksis abstrak
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) ) "), "=", Literal ( static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) ) ", BinOp (Ident ( "m"), "-", Literal ( static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) )

Abstract Syntax Trees (AST) adalah format perantara lain yang umum. Mereka terletak pada langkah berikutnya dari tangga abstraksi dibandingkan dengan kode sumber. Biasanya, AST membuang semua pemformatan kode sumber, indentasi, dan komentar, tetapi tetap menggunakan nama-nama variabel lokal yang dibuang dalam representasi yang lebih abstrak.
Seperti kode sumber, AST menderita dari kemungkinan pengkodean informasi yang tidak perlu yang tidak mempengaruhi semantik sebenarnya dari program. Sebagai contoh, dua fragmen kode berikut secara semantik identik; mereka hanya berbeda dalam nama variabel lokal, tetapi masih memiliki AST yang berbeda:
static int ackermannA(int m, int n){ int p = n; int q = m; if (q == 0) return p + 1; else if (p == 0) return ackermannA(q - 1, 1); else return ackermannA(q - 1, ackermannA(q, p - 1)); } Block( Assign("p", Ident("n")), Assign("q", Ident("m")), IfElse( cond = BinOp(Ident("q"), "==", Literal(0)), then = Return(BinOp(Ident("p"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("p"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("q"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("q"), "-", Literal(1)), Call("ackermann", Ident("q"), BinOp(Ident("p"), "-", Literal(1))) ) ) ) ) ) static int ackermannB(int m, int n){ int r = n; int s = m; if (s == 0) return r + 1; else if (r == 0) return ackermannB(s - 1, 1); else return ackermannB(s - 1, ackermannB(s, r - 1)); } Block( Assign("r", Ident("n")), Assign("s", Ident("m")), IfElse( cond = BinOp(Ident("s"), "==", Literal(0)), then = Return(BinOp(Ident("r"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("r"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("s"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("s"), "-", Literal(1)), Call("ackermann", Ident("s"), BinOp(Ident("r"), "-", Literal(1))) ) ) ) ) )
Poin kuncinya adalah bahwa walaupun AST memiliki struktur pohon, mereka mengandung node yang berperilaku semantik tidak seperti pohon: nilai-nilai
Ident("r") dan
Ident("s") ditentukan bukan oleh isi dari sub-sub-sub mereka, tetapi oleh upstream
Assign("r", ...) node-node)
Assign("r", ...) dan
Assign("s", ...) . Bahkan, ada hubungan semantik tambahan antara
Ident dan
Assign yang sama pentingnya dengan tepi dalam struktur pohon AST:

Koneksi ini membentuk struktur grafik umum, termasuk siklus dengan adanya definisi fungsi rekursif.
Bytecode
Karena kami memilih Java sebagai bahasa utama, program yang dikompilasi disimpan sebagai Java bytecode dalam file .class.
Ingat fungsi
ackermann kami:
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Ini mengkompilasi bytecode ini:
0: iload_0 1: ifne 8 4: iload_1 5: iconst_1 6: iadd 7: ireturn 8: iload_1 9: ifne 20 12: iload_0 13: iconst_1 14: isub 15: iconst_1 16: invokestatic ackermann:(II)I 19: ireturn 20: iload_0 21: iconst_1 22: isub 23: iload_0 24: iload_1 25: iconst_1 26: isub 27: invokestatic ackermann:(II)I 30: invokestatic ackermann:(II)I 33: ireturn
Java Virtual Machine (JVM), yang menjalankan bytecode Java, adalah mesin dengan kombinasi tumpukan dan register: ada tumpukan operan (STACK) di mana nilai dimanipulasi, dan array variabel lokal (LOCALS) di mana nilai-nilai ini dapat disimpan. Fungsi dimulai dengan parameter N di slot N pertama variabel lokal. Ketika dijalankan, fungsi memindahkan data ke stack, beroperasi pada mereka, menempatkan mereka kembali ke dalam variabel, memanggil
return untuk mengembalikan nilai ke pemanggil dari tumpukan operan.
Jika Anda memberi anotasi bytecode di atas untuk mewakili nilai yang bergerak antara stack dan tabel variabel lokal, itu akan terlihat seperti ini:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Di sini, menggunakan
a0 dan
a1 mempresentasikan argumen untuk fungsi, yang disimpan dalam tabel LOCALS di awal fungsi.
1 mewakili konstanta yang dimuat melalui
iconst_1 , dan dari
v1 ke
v7 , nilai tengah yang dihitung. Ada tiga instruksi untuk mengembalikan
v1 ,
v3 dan
v7 . Fungsi ini tidak mendefinisikan variabel lokal lainnya, jadi array LOCALS hanya menyimpan argumen input.
Di atas, kami melihat dua varian fungsi kami -
ackermannA dan
ackermannB . Jadi mereka mencari bytecode:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| | | a0 | BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| | | a0 | BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| | | a0 | BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| | | a0 | BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| |
Karena kode sumber mengambil dua argumen dan menempatkannya dalam variabel lokal, bytecode memiliki instruksi yang sesuai untuk memuat nilai argumen dari indeks LOCAL 0 dan 1 dan menyimpannya di bawah indeks 2 dan 3. Namun, bytecode tidak tertarik pada nama-nama variabel lokal Anda: ia bekerja dengan oleh mereka secara eksklusif seperti dengan indeks dalam array LOCALS. Oleh karena itu,
ackermannA dan
ackermannB akan memiliki bytecode yang identik. Ini logis, karena mereka secara semantik setara!
Namun,
ackermannA dan
ackermannB tidak dikompilasi ke dalam bytecode yang sama dengan
ackermann asli: meskipun bytecode diabstraksi dari nama-nama variabel lokal, itu masih tidak sepenuhnya abstrak dari memuat dan menyimpan ke / dari variabel-variabel ini. Masih penting bagi kita bagaimana nilai-nilai bergerak bersama LOKAL dan STACK, meskipun mereka tidak mempengaruhi perilaku aktual program.
Selain kurangnya abstraksi dari pemuatan / penghematan, bytecode memiliki kelemahan lain: seperti kebanyakan perakit linier, ia sangat dioptimalkan dalam hal kekompakan, dan bisa sangat sulit untuk memodifikasinya ketika datang ke optimasi.
Untuk membuatnya lebih jelas, mari kita lihat bytecode dari fungsi
ackermann asli:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Apakah perubahan kotor: biarkan fungsi panggilan
30: invokestatic ackermann:(II)I tidak menggunakan argumen pertama mereka. Dan kemudian panggilan ini dapat diganti dengan panggilan setara
30: invokestatic ackermann2:(I)I , yang hanya membutuhkan satu argumen. Ini adalah optimasi umum, yang memungkinkan menggunakan "penghapusan kode mati" untuk membuang kode apa pun yang digunakan untuk menghitung argumen pertama
30: invokestatic ackermann:(II)IUntuk melakukan ini, kita tidak hanya perlu mengganti instruksi
30 , tetapi juga perlu melihat daftar instruksi dan memahami di mana argumen pertama dihitung (
v4 dalam
STACK ), dan juga menghapusnya. Kami kembali dari instruksi
30 hingga
22 , dan dari
22 hingga
21 dan
20 . Versi terakhir:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | - 20: iload_0 |a0|a1| | - 21: iconst_1 |a0|a1| | - 22: isub |a0|a1| | 23: iload_0 |a0|a1| |a0| 24: iload_1 |a0|a1| |a0|a1| 25: iconst_1 |a0|a1| |a0|a1| 1| 26: isub |a0|a1| |a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v6| - 30: invokestatic ackermann:(II)I |a0|a1| |v7| + 30: invokestatic ackermann2:(I)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Kita masih bisa membuat perubahan sederhana ke fungsi
ackermann sederhana. Namun dalam fungsi besar yang digunakan dalam proyek-proyek nyata, itu akan jauh lebih sulit untuk membuat berbagai, perubahan saling terkait. Secara umum, setiap perubahan semantik kecil untuk program Anda mungkin memerlukan banyak perubahan sepanjang bytecode.
Anda mungkin memperhatikan bahwa kami membuat perubahan yang dijelaskan di atas dengan menganalisis nilai dalam LOCAL dan STACK: kami mengamati bagaimana
v4 diteruskan ke instruksi
30 dari instruksi
22 , dan
22 mengambil data ke
a0 dan
1 , yang berasal dari instruksi
21 dan
20 . Nilai-nilai ini ditransfer antara LOCALS dan STACK sesuai dengan prinsip grafik: dari instruksi yang menghitung nilai ke tempat penggunaan selanjutnya.
Seperti pasangan
Ident /
Assign dalam AST kami, nilai-nilai yang dikirimkan antara LOCALS dan STACK membentuk grafik antara titik-titik perhitungan nilai-nilai dan titik-titik penggunaannya. Jadi mengapa kita tidak mulai bekerja langsung dengan grafik?
Grafik Aliran Data
Grafik aliran data adalah tingkat abstraksi berikutnya setelah bytecode. Jika kami memperluas pohon sintaks kami dengan hubungan
Ident /
Assign , atau jika kami melacak bagaimana bytecode memindahkan nilai antara LOCALS dan STACK, kami dapat membuat grafik. Untuk fungsi
ackermann tampilannya seperti ini:

Tidak seperti AST atau Java stack-bytecode bytecode, grafik aliran data tidak menggunakan konsep "variabel lokal": sebaliknya, grafik berisi koneksi langsung antara setiap nilai dan di mana ia digunakan. Ketika menganalisis bytecode, seringkali perlu untuk menginterpretasikan secara LOCAL dan STACK secara abstrak untuk memahami bagaimana nilai bergerak; Analisis AST melibatkan pelacakan pohon dan bekerja dengan tabel simbol yang berisi asosiasi
Assign /
Ident ; dan menganalisis grafik aliran data sering kali merupakan pelacakan transisi secara langsung - gagasan murni "nilai-nilai bergerak" tanpa sekam menyajikan program.
ackermann juga lebih mudah untuk dimanipulasi daripada bytecode linier: mengganti sebuah node dengan
ackermann dengan
ackermann2 dan
ackermann2 salah satu argumen hanya mengubah simpul grafik (ditandai dengan warna hijau) dan menghapus salah satu tautan input bersama dengan node transit (ditandai dengan warna merah):

Seperti yang Anda lihat, perubahan kecil dalam program (mengganti
ackermann(int n, int m) dengan
ackermann2(int m) ) berubah menjadi perubahan yang relatif terlokalisasi dalam grafik aliran data.
Secara umum, bekerja dengan grafik jauh lebih mudah dibandingkan dengan bytecode linear atau AST: hanya menganalisis dan perubahan.
Tidak ada banyak detail dalam uraian grafik ini: selain representasi fisik aktual dari grafik, ada banyak cara lain untuk memodelkan kontrol keadaan dan aliran, yang lebih sulit untuk bekerja dengan dan di luar ruang lingkup artikel. Saya juga menghilangkan sejumlah detail tentang mengubah grafik, misalnya, menambahkan dan menghapus tautan, transisi maju dan mundur, transisi horizontal dan vertikal (lebar dan kedalaman), dll. Jika Anda mempelajari algoritma, maka semua ini harus Anda ketahui .
Akhirnya, kami menghilangkan algoritma konversi dari bytecode linier ke grafik, dan kemudian dari grafik kembali ke bytecode. Ini sendiri merupakan tugas yang menarik, tetapi kami serahkan kepada Anda untuk belajar mandiri.
Analisis
Setelah kami mendapatkan ide program, kami perlu menganalisanya: cari tahu beberapa fakta yang memungkinkan Anda mengubah program tanpa mengubah perilakunya. Banyak optimasi yang dibahas di atas didasarkan pada analisis program:
- Konstan lipat: Apakah hasil dari ekspresi bekerja dengan nilai konstan yang diketahui? Apakah perhitungan ekspresi murni?
- Ketik casting dan inlining: adalah metode panggilan ketik tipe dengan implementasi tunggal dari metode yang disebut?
- : ?
- : «»? - ? ?
- : , ?
, , , . , , , .
, , , — , . .
(Inference Lattice)
, . , «» - :
Integer ? String ? Array[Float] ? PrintLogger ?
CharSequence ? String , - StringBuilder ?
Any , , ?
:

: ,
"hello" String ,
String CharSequence .
"hello" , (Singleton Type) — . :

, , . , . , , ,
String StringBuilder , , :
CharSequence . ,
0 ,
1 ,
2 , ,
Integer .

, , :

, , . , .
count
main :
static int main(int n){ int count = 0, multiplied = 0; while(count < n){ if (multiplied < 100) logger.log(count); count += 1; multiplied *= count; } return ...; }
ackermann ,
count ,
multiplied logger . :

,
count 0 block0 .
block1 , ,
count < n : ,
block3 return ,
block2 ,
count 1 count ,
block1 . ,
< false ,
block3 .
?
block0 . , count = 0.
block1 , , n ( , Integer ), , if . block2 block3.block3 , , block1b , block2 , , block1c . , block2 count , 1 count.- ,
count 0 1 : count Integer. - :
block1 n count Integer .
block2 , count Integer + 1 -> Integer . , count Integer , .
multiplied
,
multiplied :
block0 . , multiplied 0.
block1 , , . block2 block3 ( ).
block2 , block2 ( 0 ) count ( Integer ). 0 * Integer -> 0 , multiplied 0.
block1 block2 . multiplied 0 , .
multiplied 0 , , :
multiplied < 100 true.
if (multiplied < 100) logger.log(count); logger.log(count) .
- ,
multiplied , , 0 .
:

:

:
static int main(int n){ int count = 0; while(count < n){ logger.log(count); count += 1; } return ...; }
, , , , .
multiplied -> 0 , , . , , . , .
, . :
count ,
multiplied . ,
multiplied count ,
count multiplied . , .
, — : , . , ( ) . .
while , ,
O( ) . (, ) , , .
, .
, . , , , , .
. :
static int main(int n){ return called(n, 0); } static int called(int x, int y){ return x * y; }
:

main :
main(n)
called(n, 0)
called(n, 0) 0
main(n) 0
, , . .
,
called(n, 0) 0 , :

:
static int main(int n){ return 0; }
: A B, C, D, D C, B, D A. A B B A, A A, , !
, Java:
public static Any factorial(int n) { if (n == 1) { return 1; } else { return n * factorial(n - 1); } }
n int ,
Any : . ,
factorial int (
Integer ).
factorial ,
factorial factorial , ! ?
Bottom
Bottom :

« , , ».
Bottom factorial :

block0 . n Integer , 1 1 , n == 1 , true false .
true : return 1 .
false n - 1 n Integer .
factorial — , Bottom .
* n: Integer factorial : Bottom Bottom .
return Bottom .factorial 1 Bottom , 1 .
1 factorial , Bottom .
Integer * 1 Integer .
return Integer .factorial Integer 1 , Integer .
factorial , Integer . * n: Integer factorial: Integer , Integer , .
factorial Integer , , .
, .
Bottom , , .
* :
(n: Integer) * (factorial: Bottom)
(n: Integer) * (factorial: 1)
(n: Integer) * (factorial: Integer)
multiplied ,
O( ) . , , .
— , « ». , (« »), , (« »). .
main :
static int main(int n){ int count = 0, total = 0, multiplied = 0; while(count < n){ if (multiplied > 100) count += 1; count += 1; multiplied *= 2; total += 1; } return count; }
,
if (multiplied > 100) multiplied *= count multiplied *= 2 . .
, :
multiplied > 100 true , count += 1 («»).
total , («»).
, :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
, .
:

, , :
block0 ,
block1 , ,
block1b , ,
block1c , ,
return block3 .
,
multiplied -> 0 , :

:

,
block1b (
0 > 100 )
true .
false block1c (
if ):
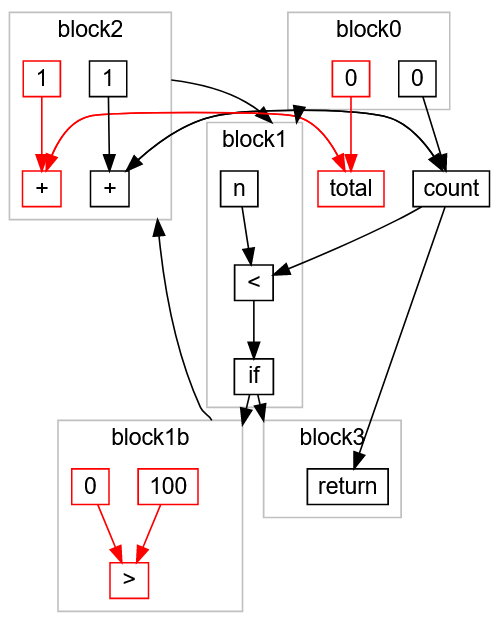
, « »
total > , - , , . ,
return ,
:
> ,
100 ,
0 block1b ,
total ,
0 ,
+ 1 ,
total block0 block2 . :

«» :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
Kesimpulan
:
- -.
- , .
- , . .
- : «» «» , , .
- : , .
- , .
, , .
, . . , :