Saya terus menerbitkan kuliah saya, awalnya ditujukan untuk siswa yang belajar di spesialisasi "geologi digital". Ini adalah publikasi ketiga dari siklus di hub, artikel pertama adalah pengantar, tidak perlu dibaca. Namun, untuk memahami artikel ini, perlu membaca pengantar sistem persamaan linear, bahkan jika Anda tahu apa itu, karena saya akan merujuk banyak contoh untuk pengantar ini.

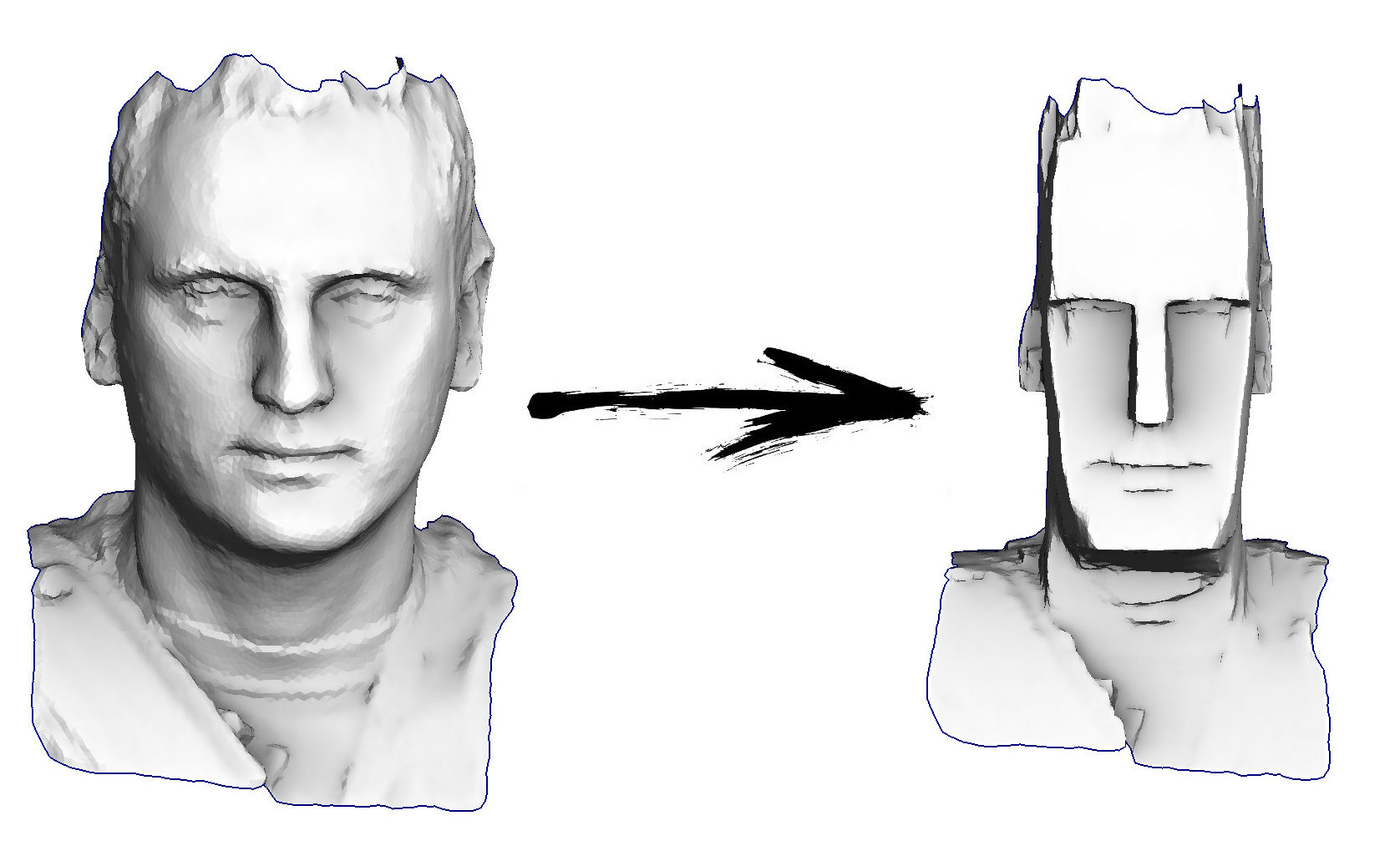
Jadi, tugas hari ini: mempelajari pemrosesan geometri yang paling sederhana, misalnya, untuk dapat mengubah kepalaku menjadi idola dari Pulau Paskah:



Rencana kuliah saat ini:

• Program pendidikan tentang teori probabilitas (artikel pengantar, opsional)
  
• Pengantar sistem persamaan linear
  
• Minimalisasi bentuk kuadratik dan contoh masalah OLS
  
• Dari Kotak Terkecil ke Jaringan Saraf Tiruan
  

Repositori kursus resmi tinggal di sini . Buku ini belum selesai, saya perlahan menyusun artikel yang diterbitkan di Habré.

Pada artikel ini, alat utama saya adalah menemukan fungsi kuadrat minimum; tetapi sebelum kita mulai menggunakan alat ini, Anda harus setidaknya memahami di mana ia memiliki tombol on / off. Pertama, menyegarkan ingatan dan mengingat matriks apa, angka positif apa, dan juga apa turunannya.

Matriks dan angka

Dalam teks ini saya akan banyak menggunakan notasi matriks, jadi mari kita ingat apa itu. Jangan melihat lebih jauh dalam teks, berhenti sebentar, dan cobalah untuk merumuskan apa itu matriks.

Interpretasi matriks yang berbeda

Jawabannya sangat sederhana. Matriks hanyalah sebuah kabinet di mana lobak disimpan. Setiap kotoran terletak di selnya, sel dikelompokkan dalam baris dalam baris dan kolom. Dalam kasus khusus kami, bilangan real yang biasa adalah omong kosong; paling mudah bagi seorang programmer untuk menyajikan sebuah matriks $$$A$ suka sesuatu

float A[m][n]; 

Mengapa penyimpanan seperti itu dibutuhkan? Apa yang mereka gambarkan? Mungkin saya akan mengecewakan Anda, tetapi matriks itu sendiri tidak menggambarkan apa pun, itu menyimpan. Misalnya, di dalamnya Anda dapat menyimpan koefisien fungsi apa pun. Mari kita lupakan matriksnya sebentar, dan bayangkan kita punya nomor $$$a$ . Apa artinya Ya, iblis tahu ... Sebagai contoh, itu mungkin suatu koefisien di dalam suatu fungsi yang mengambil satu angka sebagai input dan memberikan nomor lain sebagai output:

$$

$$f (x): \ mathbb R \ rightarrow \ mathbb R$$

Seorang ahli matematika dapat menulis satu versi dari fungsi seperti itu

$$

$$f (x) = kapak$$

Nah, di dunia programmer, akan terlihat seperti ini:

 float f(float x) { return a*x; } 

Di sisi lain, mengapa fungsi seperti itu, dan bukan yang lain? Mari kita ambil yang lain!

$$

$$f (x) = ax ^ 2$$

Sejak saya mulai tentang programmer, saya harus menulis kodenya :)

 float f(float x) { return x*a*x; } 

Salah satu dari fungsi ini adalah linear, dan yang kedua adalah kuadratik. Yang mana yang benar? Tidak, angkanya sendiri $$$a$ tidak mendefinisikannya, itu hanya menyimpan beberapa nilai! Fungsi apa yang Anda butuhkan, bangun satu seperti itu.

Hal yang sama terjadi dengan matriks, ini adalah penyimpanan yang diperlukan jika tidak ada cukup angka tunggal (skalar), semacam perluasan angka. Di atas matriks, seperti halnya angka-angka, operasi penjumlahan dan perkalian didefinisikan.

Mari kita bayangkan kita memiliki matriks $$$A$ Misalnya, ukuran 2x2:

$$

$$A = \ begin {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix}$$

Matriks ini sendiri tidak berarti apa-apa, misalnya, dapat diartikan sebagai fungsi

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2, \ quad f (x) = Ax$$

 vector<float> f(vector<float> x) { return vector<float>{a11*x[0] + a12*x[1], a21*x[0] + a22*x[1]}; } 

Fungsi ini mengubah vektor dua dimensi menjadi vektor dua dimensi. Secara grafis, mudah untuk menyajikan ini sebagai konversi gambar: kami memberikan gambar ke input, dan pada output kami mendapatkan versi yang diregangkan dan / atau diputar (bahkan mungkin dicerminkan!). Segera saya akan memberikan gambar dengan berbagai contoh interpretasi seperti matriks.

Dan bisa dengan matriks $$$A$ bayangkan sebagai fungsi yang mengubah vektor dua dimensi menjadi skalar:

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R, \ quad f (x) = x ^ \ top A x = \ jumlah \ limit_i \ jumlah \ limit_j a_ {ij} x_i x_j$$

Perhatikan bahwa eksponensial tidak terlalu didefinisikan dengan vektor, jadi saya tidak bisa menulis $$$x ^ 2$ , Seperti yang ia tulis dalam kasus angka biasa. Saya sangat merekomendasikan bagi mereka yang tidak terbiasa dengan mudah menangani perkalian matriks, sekali lagi mengingat aturan perkalian matriks, dan memverifikasi bahwa ekspresi $$$x ^ \ top A x$ umumnya diizinkan dan benar-benar memberikan skalar di pintu keluar. Untuk melakukan ini, misalnya, Anda dapat memasang tanda kurung secara eksplisit $$$x ^ \ top A x = (x ^ \ top A) x$ . Saya mengingatkan Anda bahwa kami punya $$$x$ Adalah vektor dimensi 2 (disimpan dalam matriks dimensi 2x1), kami menulis secara eksplisit semua dimensi:

$$

$$\ underbrace {\ underbrace {\ left (\ underbrace {x ^ \ top} _ {1 \ times 2} \ times \ underbrace {A} _ {2 \ times 2} \ kanan)} _ {1 \ times 2} \ times \ underbrace {x} _ {2 \ times 1}} _ {1 \ times 1}$$

Kembali ke dunia programmer yang hangat dan lembut, kita dapat menulis fungsi kuadratik yang sama seperti ini:

 float f(vector<float> x) { return x[0]*a11*x[0] + x[0]*a12*x[1] + x[1]*a21*x[0] + x[1]*a22*x[1]; } 

Apa itu angka positif?

Sekarang saya akan mengajukan pertanyaan yang sangat bodoh: berapakah angka positif? Kami memiliki alat hebat yang disebut predikat lagi $$$>$ . Tetapi luangkan waktu Anda untuk menjawab nomor itu $$$a$ positif jika dan hanya jika $$$a> 0$ Itu terlalu mudah. Mari kita definisikan positif sebagai berikut:

Definisi 1

Nomor $$$a$ positif jika dan hanya jika untuk semua bukan nol nyata $$$x \ dalam \ mathbb R, \ x \ neq 0$ kondisinya puas $$$ax ^ 2> 0$ .

Ini terlihat sangat rumit, tetapi ini berlaku untuk matriks:

Definisi 2

Matriks persegi $$$A$ disebut positif pasti jika, untuk bukan nol $$$x$ kondisinya puas $$$x ^ \ top A x> 0$ yaitu, bentuk kuadratik yang sesuai benar-benar positif di mana-mana kecuali asal.

Mengapa saya perlu kepositifan? Seperti yang saya sebutkan di awal artikel, alat utama saya adalah mencari minimum fungsi kuadratik. Tetapi untuk setidaknya mencari, itu tidak akan buruk jika ada! Misalnya, suatu fungsi $$$f (x) = - x ^ 2$ minimum jelas tidak ada, karena angka -1 tidak positif, dan $$$f (x)$ berkurang tanpa henti dengan pertumbuhan $$$x$ : cabang parabola $$$f (x)$ lihat ke bawah. Matriks pasti positif baik karena bentuk kuadrat yang sesuai membentuk parabola yang memiliki minimum (unik). Ilustrasi berikut menunjukkan tujuh contoh matriks yang berbeda. $$$2 \ kali 2$ , pasti positif dan simetris, dan tidak begitu. Baris atas: interpretasi matriks sebagai fungsi $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2$ . Baris tengah: interpretasi matriks sebagai fungsi $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R$ .



Dengan demikian, saya akan bekerja dengan matriks pasti positif, yang merupakan generalisasi dari angka positif. Selain itu, khususnya dalam kasus saya, matriks juga akan simetris! Sangat mengherankan bahwa cukup sering ketika orang berbicara tentang kepastian positif, mereka juga menyiratkan simetri, yang dapat secara tidak langsung dijelaskan oleh pengamatan berikut (opsional untuk memahami teks berikutnya).

Penyimpangan liris pada simetri matriks bentuk kuadrat

Mari kita lihat bentuk kuadratik $$$x ^ \ top M x$ untuk matriks arbitrer $$$M$ ; lalu ke $$$M$ tambahkan dan segera kurangi setengah dari versi yang dipindahkan:

$$

$$M = \ underbrace {\ frac {1} {2} (M + M ^ \ top)} _ {: = M_s} + \ underbrace {\ frac {1} {2} (MM ^ \ top)} _ { : = M_a} = M_s + M_a$$

Matriks $$$M_s$ simetris: $$$M_s ^ \ top = M_s$ ; matriks $$$M_a$ antisimetri: $$$M_a ^ \ top = -M_a$ . Fakta yang luar biasa adalah bahwa untuk setiap matriks antisimetri, bentuk kuadratik yang sesuai sama dengan nol. Ini mengikuti dari pengamatan berikut:

$$

$$q = x ^ \ top M_a x = (x ^ \ top M_a ^ \ top x) ^ \ top = - (x ^ \ top M_a x) ^ \ top = -q$$

Artinya, bentuk kuadratik $$$x ^ \ top M_a x$ secara bersamaan sama $$$q$ dan $$$-q$ , yang hanya mungkin bila $$$q \ equiv 0$ . Dari fakta ini berarti bahwa untuk matriks arbitrer $$$M$ bentuk kuadrat yang sesuai $$$x ^ \ top M x$ dapat diekspresikan melalui matriks simetris $$$M_s$ :

$$

$$x ^ \ top M x = x ^ \ top (M_s + M_a) x = x ^ \ top M_s x + x ^ \ top M_a x = x ^ \ top M_s x.$$

Kami mencari fungsi kuadrat minimum

Mari kita kembali sebentar ke dunia satu dimensi; Saya ingin mencari fungsi minimum $$$f (x) = ax ^ 2 - 2bx$ . Nomor $$$a$ positif, oleh karena itu minimum ada; untuk menemukannya, kami menyamakan dengan nol turunan yang sesuai: $$$\ frac {d} {dx} f (x) = 0$ . Membedakan fungsi kuadratik satu dimensi dari persalinan bukanlah: $$$\ frac {d} {dx} f (x) = 2ax - 2b = 0$ ; jadi masalah kita bermuara pada penyelesaian persamaan $$$ax-b = 0$ , di mana, melalui upaya yang mengerikan, kami mendapatkan solusi $$$x ^ * = b / a$ . Gambar berikut menggambarkan kesetaraan dua masalah: solusi $$$x ^ *$ persamaan $$$ax-b = 0$ bertepatan dengan solusi persamaan $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ .



Saya cenderung pada fakta bahwa tujuan global kami adalah untuk meminimalkan fungsi kuadrat, tetapi kita berbicara tentang kuadrat terkecil. Tetapi pada saat yang sama, apa yang benar-benar kita ketahui bagaimana melakukannya dengan baik adalah menyelesaikan persamaan linear (dan sistem persamaan linear). Dan sangat keren bahwa satu setara dengan yang lain!

Satu-satunya hal yang tersisa bagi kita adalah memastikan bahwa kesetaraan dalam dunia satu dimensi ini meluas ke kasus ini $$$n$ variabel. Untuk memverifikasi ini, pertama-tama kita membuktikan tiga teorema.

Tiga teorema, atau membedakan ekspresi matriks

Teorema pertama menyatakan bahwa matriks $$$1 \ kali 1$ invarian terkait dengan transposisi:

Teorema 1

$$$x \ in \ mathbb R \ Rightarrow x ^ \ top = x$

Buktinya sangat rumit sehingga saya harus menghilangkannya untuk singkatnya, tetapi cobalah untuk menemukannya sendiri.

Teorema kedua memungkinkan kita untuk membedakan fungsi-fungsi linear. Dalam kasus fungsi nyata dari satu variabel, kita tahu itu $$$\ frac {d} {dx} (bx) = b$ tetapi apa yang terjadi dalam kasus fungsi nyata $$$n$ variabel?

Teorema 2

$$$\ nabla b ^ \ top x = \ nabla x ^ \ top b = b$

Artinya, tidak ada kejutan, hanya rekaman matriks hasil sekolah yang sama. Buktinya sangat mudah, cukup tulis definisi gradien:

$$

$$\ nabla (b ^ \ top x) = \ begin {bmatrix} \ frac {\ partial (b ^ \ top x)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partial (b ^ \ top x)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} \ frac {\ partial (b_1 x_1 + \ dots + b_n x_n)} {\ partial x_1} \\ \ vdots \\ \ frac {\ parsial (b_1 x_1 + \ dots + b_n x_n)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} b_1 \\ \ vdots \\ b_n \ end {bmatrix} = b$$

Menerapkan teorema pertama $$$b ^ \ top x = x ^ \ top b$ , kami melengkapi buktinya.

Sekarang kita beralih ke bentuk kuadratik. Kita tahu bahwa dalam kasus fungsi nyata dari satu variabel $$$\ frac {d} {dx} (ax ^ 2) = 2 max$ , dan apa yang akan terjadi dalam kasus bentuk kuadratik?

Teorema 3

$$$\ nabla (x ^ \ top A x) = (A + A ^ \ top) x$

By the way, perhatikan bahwa jika matriks $$$A$ simetris, maka teorema mengatakan itu $$$\ nabla (x ^ \ top A x) = 2Ax$ .

Bukti ini juga mudah, cukup tulis bentuk kuadratik sebagai jumlah ganda:

$$

$$x ^ \ atas A x = \ jumlah \ limit_i \ jumlah \ limit_j a_ {ij} x_i x_j$$

Dan kemudian mari kita lihat apa turunan parsial dari jumlah ganda ini sehubungan dengan variabel $$$x_i$ :
\ begin {align *}
\ frac {\ partial (x ^ \ top A x)} {\ partial x_i}
& = \ frac {\ partial} {\ partial x_i} \ kiri (\ jumlah \ limit_ {k_1} \ jumlah \ limit_ {k_2} a_ {k_1 k_2} x_ {k_1} x_ {k_2} \ kanan) = \\
& = \ frac {\ partial} {\ partial x_i} \ kiri (
\ underbrace {\ jumlah \ limit_ {k_1 \ neq i} \ jumlah \ limit_ {k_2 \ neq i} a_ {ik_2} x_ {k_1} x_ {k_2}} _ {k_1 \ neq i, k_2 \ neq i} + underbrace {\ jumlah \ limit_ {k_2 \ neq i} a_ {ik_2} x_i x_ {k_2}} _ {k_1 = i, k_2 \ neq i} +
\ underbrace {\ sum \ limit_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} x_i} _ {k_1 \ neq i, k_2 = i} +
\ underbrace {a_ {ii} x_i ^ 2} _ {k_1 = i, k_2 = i} \ kanan) = \\
& = \ jumlah \ limit_ {k_2 \ neq i} a_ {ik_2} x_ {k_2} + \ jumlah \ limit_ {k_1 \ neq i} a_ {k_1 saya} x_ {k_1} + 2 a_ {ii} x_i = \\
& = \ jumlah \ limit_ {k_2} a_ {ik_2} x_ {k_2} + \ sum \ limit_ {k_1} a_ {k_1 i} x_ {k_1} = \\
& = \ jumlah \ limit_ {j} (a_ {ij} + a_ {ji}) x_j \\
\ end {align *}
Saya membagi jumlah ganda menjadi empat kasus, yang disorot oleh kawat gigi. Masing-masing dari empat kasus ini berbeda sepele. Masih melakukan tindakan terakhir, mengumpulkan turunan parsial dalam vektor gradien:

$$

$$\ nabla (x ^ \ top A x) = \ begin {bmatrix} \ frac {\ partial (x ^ \ Axe atas)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partial (x ^ \ top A x)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} \ jumlah \ Limit_ {j} (a_ {1j} + a_ {j1}) x_j \\ \ vdots \\ \ sum \ limit_ {j} (a_ {nj} + a_ {jn}) x_j \ end {bmatrix} = (A + A ^ \ top) x$$

Minimum fungsi kuadratik dan solusi sistem linier

Jangan lupa arah perjalanan. Kami melihat itu dengan angka positif $$$a$ dalam kasus fungsi nyata dari satu variabel, pecahkan persamaannya $$$ax = b$ atau meminimalkan fungsi kuadratik $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ Adalah satu hal yang sama.

Kami ingin menunjukkan koneksi yang sesuai dalam kasus matriks definitif positif simetris $$$A$ .
Jadi kami ingin menemukan fungsi kuadrat minimum

$$

$$\ mathrm {argmin} _ {x \ in \ mathbb R ^ n} (x ^ \ top A x - 2b ^ \ top x).$$

Persis seperti di sekolah, kami menyamakan turunan ke nol:

$$

$$\ nabla (x ^ \ top A x - 2b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}.$$

Operator Hamilton adalah linier, sehingga kami dapat menulis ulang persamaan kami dalam bentuk berikut:

$$

$$\ nabla (x ^ \ top A x) - 2 \ nabla (b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Sekarang kita menerapkan teorema diferensiasi kedua dan ketiga:

$$

$$(A + A ^ \ atas) x - 2b = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Ingat itu $$$A$ simetris, dan membagi persamaan menjadi dua, kita mendapatkan sistem persamaan linear yang kita butuhkan:

$$

$$Ax = b$$

Hore, pindah dari satu variabel ke banyak, kita tidak kehilangan apa-apa, dan kita dapat secara efektif meminimalkan fungsi kuadratik!

Kami melewati kuadrat terkecil

Akhirnya, kita bisa beralih ke konten utama dari kuliah ini. Bayangkan kita memiliki dua poin di pesawat $$$(x_1, y_1)$ dan $$$(x_2, y_2)$ , dan kami ingin menemukan persamaan garis yang melewati dua titik ini. Persamaan garis dapat ditulis sebagai $$$y = \ alpha x + \ beta$ , yaitu, tugas kami adalah menemukan koefisien $$$\ alpha$ dan $$$\ beta$ . Latihan ini untuk kelas tujuh-delapan sekolah, kami menuliskan sistem persamaan:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ end {split} \ kanan.$$

Kami memiliki dua persamaan dengan dua tidak diketahui ( $$$\ alpha$ dan $$$\ beta$ ), sisanya diketahui.

Dalam kasus umum, solusi ada dan unik. Untuk kenyamanan, kami menulis ulang sistem yang sama dalam bentuk matriks:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \ end {bmatrix}} _ {: = A} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \ end {bmatrix}} _ {: = b}$$

Kami mendapatkan persamaan tipe $$$Ax = b$ yang sepele dipecahkan $$$x ^ * = A ^ {- 1} b$ .

Sekarang bayangkan bahwa kita memiliki tiga poin di mana kita perlu menggambar garis lurus:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ alpha x_3 + \ beta & = y_3 \\ \ end {split} \ kanan .$$

Dalam bentuk matriks, sistem ini ditulis sebagai berikut:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix}} _ {: = A \, (3 \ kali 2)} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x \, (2 \ kali 1)} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}} _ { : = b \, (3 \ kali 1)}$$

Sekarang kita memiliki matriks $$$A$ persegi panjang, dan itu tidak ada terbalik! Ini sepenuhnya normal, karena kita hanya memiliki dua variabel dan tiga persamaan, dan dalam kasus umum sistem ini tidak memiliki solusi. Ini adalah situasi yang benar-benar normal di dunia nyata, ketika poinnya adalah data dari pengukuran bising, dan kita perlu menemukan parameternya $$$\ alpha$ dan $$$\ beta$ data pengukuran perkiraan terbaik. Kami sudah mempertimbangkan contoh ini di kuliah pertama, ketika dikalibrasi stely. Tapi kemudian solusi kami murni aljabar dan sangat rumit. Mari kita coba cara yang lebih intuitif.

Sistem kami dapat ditulis sebagai berikut:

$$

$$\ alpha \ underbrace {\ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix}} _ {: = \ vec {i}} + \ beta \ underbrace {\ begin {bmatrix} 1 \\ 1 \ \ 1 \ end {bmatrix}} _ {: = \ vec {j}} = \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}$$

Atau, lebih singkat,

$$

$$\ alpha \ vec {i} + \ beta \ vec {j} = \ vec {b}.$$

Vektor $$$\ vec i$ , $$$\ vec j$ dan $$$\ vec b$ diketahui, perlu menemukan skalar $$$\ alpha$ dan $$$\ beta$ .
Kombinasi yang jelas linier $$$\ alpha \ vec {i} + \ beta \ vec {j}$ memunculkan pesawat, dan jika vektor $$$\ vec b$ tidak berbaring di pesawat ini, maka tidak ada solusi yang tepat; namun, kami mencari solusi perkiraan.

Mari kita mendefinisikan kesalahan keputusan sebagai $$$\ vec {e} (\ alpha, \ beta): = \ alpha \ vec {i} + \ beta \ vec {j} - \ vec b$ . Tujuan kami adalah menemukan nilai parameter tersebut $$$\ alpha$ dan $$$\ beta$ yang meminimalkan panjang vektor $$$\ vec {e} (\ alpha, \ beta)$ . Dengan kata lain, masalahnya ditulis sebagai $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ .
Berikut ini ilustrasi:.



Setelah diberi vektor $$$\ vec i$ , $$$\ vec j$ dan $$$\ vec b$ , kami mencoba meminimalkan panjang vektor kesalahan $$$\ vec e$ . Jelas, panjangnya diminimalkan jika tegak lurus terhadap bidang yang direntangkan di atas vektor $$$\ vec i$ dan $$$\ vec j$ .

Tapi tunggu, di mana kotak paling sedikit? Sekarang mereka akan menjadi. Fungsi ekstraksi akar $$$\ sqrt {\ cdot}$ karena itu monoton $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ = $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ !

Cukup jelas bahwa panjang vektor kesalahan diminimalkan jika tegak lurus terhadap bidang yang direntangkan di atas vektor $$$\ vec i$ dan $$$\ vec j$ , yang dapat ditulis dengan menyamakan dengan nol produk skalar yang sesuai:

$$

$$\ left \ {\ begin {split} \ vec {i} ^ \ top \ vec {e} (\ alpha, \ beta) & = 0 \\ \ vec {j} ^ \ top \ vec {e} (\ alpha, \ beta) & = 0 \ end {split} \ benar.$$

Dalam bentuk matriks, sistem yang sama ini dapat ditulis sebagai

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ kiri (\ alpha \ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix} + \ beta \ begin {bmatrix} 1 \\ 1 \\ 1 \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ kanan) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix }$$

atau yang lainnya

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ kiri (\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix} \ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ kanan) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix }$$

Tapi kami tidak akan berhenti di situ, karena catatan dapat dikurangi lebih lanjut:

$$

$$A ^ \ top (Ax - b) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix}$$

Dan transformasi terbaru:

$$

$$A ^ \ top Axe = A ^ \ top b.$$

Mari kita hitung dimensi. Matriks $$$A$ memiliki ukuran $$$3 \ kali 2$ oleh karena itu $$$A ^ \ top A$ memiliki ukuran $$$2 \ kali 2$ . Matriks $$$b$ memiliki ukuran $$$3 \ kali 1$ tetapi vektor $$$A ^ \ top b$ memiliki ukuran $$$2 \ kali 1$ . Yaitu, dalam kasus umum, matriks $$$A ^ \ top A$ reversibel! Selain itu, $$$A ^ \ top A$ Ini memiliki beberapa properti yang bagus.

Teorema 4

$$$A ^ \ top A$ simetris.

Ini sama sekali tidak sulit untuk ditunjukkan:

$$

$$(A ^ \ top A) ^ \ top = A ^ \ top (A ^ \ top) ^ \ top = A ^ \ top A.$$

Teorema 5

$$$A ^ \ top A$ semi-pasti positif: $$$\ forall x \ in \ mathbb R ^ n \ quad x ^ \ top A ^ \ top A x \ geq 0.$

Ini mengikuti dari kenyataan itu $$$x ^ \ top A ^ \ top A x = (A x) ^ \ top A x> 0$ .

Juga $$$A ^ \ top A$ pasti positif jika $$$A$ memiliki kolom bebas linear (peringkat $$$A$ sama dengan jumlah variabel dalam sistem).

Secara total, untuk sistem dengan dua yang tidak diketahui, kami membuktikan bahwa meminimalkan fungsi kuadratik $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ setara dengan memecahkan sistem persamaan linear $$$A ^ \ top A x = A ^ \ top b$ . Tentu saja, semua alasan ini berlaku untuk sejumlah variabel lainnya, tetapi mari kita kompak menulis semuanya lagi dengan perhitungan aljabar sederhana. Kita mulai dengan masalah kuadrat terkecil, sampai pada minimalisasi fungsi kuadratik dari bentuk yang sudah dikenal, dan dari sini kita menyimpulkan bahwa itu setara dengan memecahkan sistem persamaan linear. Jadi, ayo pergi:

$$

$$\ begin {split} \ mathrm {argmin} \ | Kapak - b \ | ^ 2 & = \ mathrm {argmin} (Ax-b) ^ \ top (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top - b ^ \ top) (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - b ^ \ top Axe - x ^ \ top A ^ \ top b + \ underbrace {b ^ \ top b} _ {\ rm const}) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - 2b ^ \ top Axe) = \\ & = \ mathrm {argmin} ( x ^ \ top \ underbrace {(A ^ \ top A)} _ {: = A '} x - 2 \ underbrace {(A ^ \ top b)} _ {: = b'} \ phantom {} ^ \ top x) \ end {split}$$

Jadi masalah kuadrat terkecil $$$\ mathrm {argmin} \ | Ax - b \ | ^ 2$ setara dengan meminimalkan fungsi kuadratik $$$\ mathrm {argmin} (x ^ \ top A 'x - 2b' ^ \ top x)$ dengan (dalam kasus umum) matriks pasti positif simetris $$$A '$ , yang, pada gilirannya, sama dengan memecahkan sistem persamaan linear $$$A'x = b '$ . Uff. Teorinya sudah berakhir.

Mari kita lanjutkan berlatih

Contoh Satu, Satu Dimensi

Mari kita ingat satu contoh dari artikel sebelumnya :

 # initialize the data array x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. # smooth the array values other than at indices 0,18,31 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1] + x[i+1])/2. 

Kami memiliki x array reguler dari 32 elemen, diinisialisasi sebagai berikut:



Dan kemudian kita akan melakukan prosedur berikut ini ribuan kali: untuk setiap sel x [i] kita menuliskan nilai rata-rata sel tetangga ke dalamnya: x [i] = (x [i-1] + x [i + 1]) / 2. Satu-satunya pengecualian: kami tidak akan menulis ulang elemen array dengan angka 0, 18 dan 31. Ini adalah bagaimana evolusi array terlihat dalam seratus lima puluh iterasi pertama:



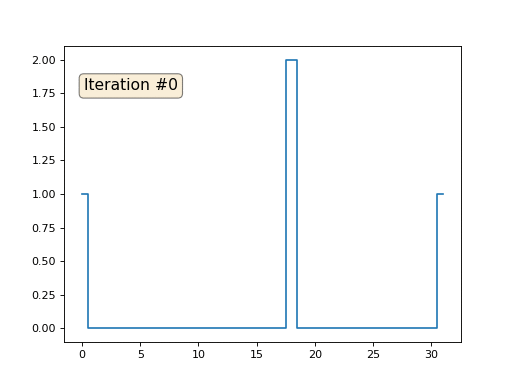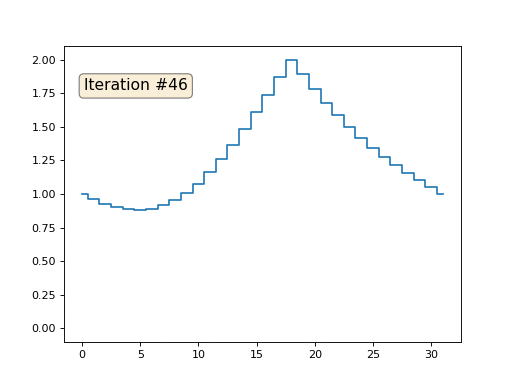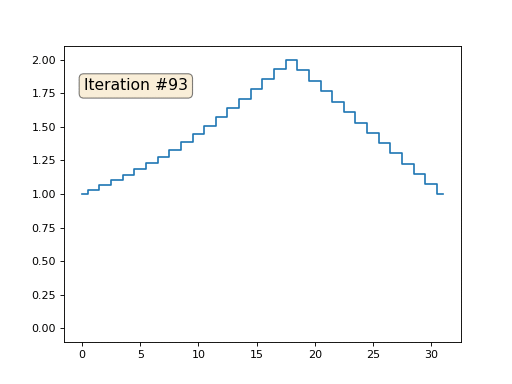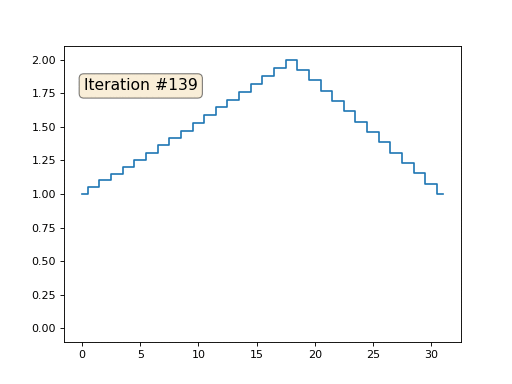
Seperti yang kami temukan di artikel sebelumnya , ternyata megacode kode python empat baris kami menyelesaikan sistem persamaan linear berikut dengan metode Gauss-Seidel:



Mereka tahu, tetapi dari mana sistem ini berasal? Sihir macam apa? Mari kita menyimpang sebentar, dan mencoba memecahkan sistem yang sedikit berbeda. Saya masih memiliki 32 variabel, tetapi sekarang saya ingin mereka semua sama-sama sama satu sama lain. Ini tidak sulit untuk ditulis, cukup untuk menuliskan sistem persamaan yang menyatakan bahwa semua elemen tetangga adalah sama berpasangan:



Kode Python di atas, pada prinsipnya, tidak menyentuh nilai-nilai dari tiga variabel: x0, x18, x31, jadi mari kita transfer mereka ke sisi kanan sistem persamaan, yaitu, mengecualikan dari set yang tidak diketahui:



Saya memperbaiki nilai awal x0 = 1, persamaan pertama mengatakan x1 = x0 = 1, persamaan kedua mengatakan x2 = x1 = x0 = 1 dan seterusnya, sampai kita mencapai persamaan 1 = x0 = x17 = x18 = 2 Oh Tetapi sistem ini tidak memiliki solusi: ((

Dan tidak peduli, kami adalah programmer! Mari kita hubungi kuadrat terkecil untuk bantuan! Sistem kami yang tidak dapat diselesaikan dapat ditulis dalam bentuk matriks $$$Ax = b$ ; untuk menyelesaikan sistem kami, cukup untuk menyelesaikan sistem $$$A^\top Ax=A^\top b$ .Dan ternyata ini adalah sistem persamaan satu-satu dari artikel sebelumnya!

Secara intuitif, kita dapat membayangkan proses menciptakan matriks sistem sebagai berikut: kita terhubung dengan memunculkan nilai-nilai yang ingin dicapai kesetaraannya. Sebagai contoh, dalam kasus kami, kami inginkan$$x saya sama$x_i$$$x i + 1 , jadi kita tambahkan persamaan$x_{i+1}$$$$x_i - x_{i+1}=0$ , , . x0, x18 x31 , , , ( ) - .

, . , - , , . , , - :

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # eliminate the constrained variables from the matrix A = A[:,[*range(1,18)] + [*range(19,31)]] b = np.matrix(np.zeros((n-1, 1))) b[0,0] = 1. b[17,0] = -2. b[18,0] = 2. b[n-2,0] = -1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] # re-introduce the constrained variables x.insert(0, 1.) x.insert(18, 2.) x.append(1.) 

x 32 , . $$A , membangun vektor$A$$$b , kami mendapatkan vektor dengan solusi$b$$$x = ( A ⊤ A ) - 1 A ⊤ b , dan kemudian kami memasukkan nilai tetap kami x0 = 1, x18 = 2 dan x31 = 1 ke dalam vektor ini. Kode ini berfungsi, tetapi agak tidak menyenangkan untuk mentransfer nilai variabel tetap ke sisi kanan. Apakah mungkin menipu? Kamu bisa! Mari kita lihat kode berikut:$x = (A^\top A)^{-1}A^\top b$

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1+3, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # enforce the constraints through the quadratic penalty A[n-1+0, 0] = 100. A[n-1+1,18] = 100. A[n-1+2,31] = 100. b = np.matrix(np.zeros((n-1+3, 1))) b[n-1+0,0] = 100.*1. b[n-1+1,0] = 100.*2. b[n-1+2,0] = 100.*1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] 

, x , A b . ? , :



:
100 x0 = 100 * 1
100 x18 = 100 * 2
100 x31 = 100 * 1

?
x0 = 1
x18 = 2
x31 = 1

, . , , x0 1, x18 2 , , x31 .

100 . , , , . 100 , x0, x18 x32 , (100^2) $$$x_i = x_{i+1}$ . , , . — , ( ), .

,

- , ! , . , , :



, :

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

wavefront .obj , . OpenNL, . , : , / 1000 x 1000 , $$A ⊤ A kita akan memiliki ukuran satu juta per juta! Namun, dalam praktiknya, paling sering sebagian besar elemen dari matriks ini adalah nol, jadi semuanya tidak begitu menakutkan, tetapi Anda masih perlu menggunakan pemecah khusus. Jadi mari kita lihat kodenya. Untuk memulai, saya mengumumkan kepada pemecah apa yang ingin saya lakukan:$A^\top A$

  nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); 

Saya ingin memiliki matriks $$A ⊤ A dalam ukuran (jumlah simpul) x (jumlah simpul). Perhatian, kami memberikan pemecah sebuah matriks$A^\top A$$$A , dan$A$$$$A^\top A$ , ! , , x,y z ( , , - !)

. , :

  for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } 

, 100^2 .

1 :

  for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } 

, . , .

:



, , , :

  for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } 

. ? , , . (, 0.2) , , , :

  for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } 

, , , : , .

!

  for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } 

. , , , .

.

, . - , , , . , :

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" const Vec3f axes[] = {Vec3f(1,0,0), Vec3f(-1,0,0), Vec3f(0,1,0), Vec3f(0,-1,0), Vec3f(0,0,1), Vec3f(0,0,-1)}; int snap(Vec3f n) { // returns the coordinate axis closest to the given normal double nmin = -2.0; int imin = -1; for (int i=0; i<6; i++) { double t = n*axes[i]; if (t>nmin) { nmin = t; imin = i; } } return imin; } int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); std::vector<int> nearest_axis(m.nfaces()); for (int i=0; i<m.nfaces(); i++) { Vec3f v[3]; for (int j=0; j<3; j++) v[j] = m.point(m.vert(i, j)); Vec3f n = cross(v[1]-v[0], v[2]-v[0]).normalize(); nearest_axis[i] = snap(n); } for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); int axis = nearest_axis[i/3]/2; if (d!=axis) continue; nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

- , ; snap() . , . , , . , , , ! snap():



, , . :

  nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); 

Yaitu, kami menginstruksikan setiap tepi permukaan output untuk menyerupai tepi yang sesuai dari permukaan input, kekakuan pegas 1. Dan kemudian, jika kita membiarkan, misalnya, dimensi x, dan tepi harus vertikal, maka kita hanya mengatakan bahwa satu simpul sama dengan yang lain dengan kekakuan pegas 2:

  nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); 

Nah, inilah hasil dari program kami:



Pertanyaan yang masuk akal: berhala-berhala dari Pulau Paskah, ini, tentu saja, keren, tapi apa hubungannya geologi dengan itu? Apakah ada contoh masalah nyata?

Ya tentu saja :



, () , , . ( 3) , , ( 3). , , () :



, , , .

Kesimpulan

— , , . , — , () , .

, . , , . , . !