Dimengerti RayTracing dalam 256 baris telanjang C ++
Ini adalah bab lain dari kuliah singkat saya tentang grafik komputer . Kali ini kita berbicara tentang penelusuran sinar. Seperti biasa, saya mencoba menghindari perpustakaan pihak ketiga, karena saya percaya itu membuat siswa memeriksa apa yang terjadi di bawah tenda. Periksa juga proyek tinykaboom .
Ada banyak artikel raytracing di web; namun masalahnya adalah bahwa hampir semuanya menunjukkan perangkat lunak yang sudah jadi yang bisa sangat sulit untuk dipahami. Ambil, misalnya, tantangan pelacak ray kartu bisnis yang sangat terkenal. Ini menghasilkan program yang sangat mengesankan, tetapi sangat sulit untuk memahami cara kerjanya. Daripada menunjukkan bahwa saya dapat melakukan rendering, saya ingin memberi tahu Anda secara rinci bagaimana Anda bisa melakukannya sendiri.
Catatan: Tidak masuk akal hanya untuk melihat kode saya, atau hanya membaca artikel ini dengan secangkir teh di tangan. Artikel ini dirancang agar Anda dapat menggunakan keyboard dan menerapkan mesin rendering Anda sendiri. Itu pasti akan lebih baik daripada milikku. Paling tidak ubahlah bahasa pemrograman!
Jadi, tujuan hari ini adalah mempelajari cara membuat gambar seperti itu:

Langkah 1: menulis gambar ke disk
Saya tidak ingin repot dengan manajer jendela, pemrosesan mouse / keyboard dan hal-hal seperti itu. Hasil dari program kami adalah gambar sederhana yang disimpan di disk. Jadi, hal pertama yang perlu kita lakukan adalah menyimpan gambar ke disk. Di sini Anda dapat menemukan kode yang memungkinkan kami melakukan ini. Biarkan saya daftar file utama:
#include <limits> #include <cmath> #include <iostream> #include <fstream> #include <vector> #include "geometry.h" void render() { const int width = 1024; const int height = 768; std::vector<Vec3f> framebuffer(width*height); for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } } std::ofstream ofs; // save the framebuffer to file ofs.open("./out.ppm"); ofs << "P6\n" << width << " " << height << "\n255\n"; for (size_t i = 0; i < height*width; ++i) { for (size_t j = 0; j<3; j++) { ofs << (char)(255 * std::max(0.f, std::min(1.f, framebuffer[i][j]))); } } ofs.close(); } int main() { render(); return 0; }
Hanya render () yang dipanggil dalam fungsi utama dan tidak ada yang lain. Apa yang ada di dalam fungsi render ()? Pertama-tama, saya mendefinisikan framebuffer sebagai array satu dimensi dari nilai Vec3f, yaitu vektor tiga dimensi sederhana yang memberi kita (r, g, b) nilai untuk setiap piksel. Kelas vektor tinggal di file geometry.h, saya tidak akan menjelaskannya di sini: itu benar-benar manipulasi sepele dari vektor dua dan tiga dimensi (penambahan, pengurangan, penugasan, perkalian dengan skalar, produk skalar).
Saya menyimpan gambar dalam format ppm . Ini adalah cara termudah untuk menyimpan gambar, meskipun tidak selalu cara yang paling nyaman untuk melihatnya lebih jauh. Jika Anda ingin menyimpan dalam format lain, saya sarankan Anda menautkan perpustakaan pihak ketiga, seperti stb . Ini adalah perpustakaan yang hebat: Anda hanya perlu memasukkan satu file header stb_image_write.h dalam proyek, dan itu akan memungkinkan Anda untuk menyimpan gambar dalam format paling populer.
Peringatan: kode saya penuh dengan bug, saya memperbaikinya di hulu, tetapi komitmen yang lebih lama terpengaruh. Lihat masalah ini .
Jadi, tujuan dari langkah ini adalah untuk memastikan bahwa kita dapat a) membuat gambar dalam memori + menetapkan warna yang berbeda dan b) menyimpan hasilnya ke disk. Kemudian Anda dapat melihatnya di perangkat lunak pihak ketiga. Inilah hasilnya:

Langkah 2, yang penting: penelusuran sinar
Ini adalah langkah paling penting dan sulit dari keseluruhan rantai. Saya ingin mendefinisikan satu bola dalam kode saya dan menggambarnya tanpa terobsesi dengan bahan atau pencahayaan. Beginilah hasilnya akan terlihat seperti:

Demi kenyamanan, saya memiliki satu komit per langkah dalam repositori saya; Github membuatnya sangat mudah untuk melihat perubahan yang dilakukan. Di sini, misalnya , apa yang diubah oleh komit kedua.
Untuk memulainya, apa yang kita butuhkan untuk mewakili lingkup dalam memori komputer? Empat angka sudah cukup: vektor tiga dimensi untuk pusat bola dan skalar yang menggambarkan jari-jari:
struct Sphere { Vec3f center; float radius; Sphere(const Vec3f &c, const float &r) : center(c), radius(r) {} bool ray_intersect(const Vec3f &orig, const Vec3f &dir, float &t0) const { Vec3f L = center - orig; float tca = L*dir; float d2 = L*L - tca*tca; if (d2 > radius*radius) return false; float thc = sqrtf(radius*radius - d2); t0 = tca - thc; float t1 = tca + thc; if (t0 < 0) t0 = t1; if (t0 < 0) return false; return true; } };
Satu-satunya hal non-sepele dalam kode ini adalah fungsi yang memungkinkan Anda untuk memeriksa apakah sinar yang diberikan (berasal dari asal dalam arah dir) berpotongan dengan bola kami. Penjelasan terperinci dari algoritma untuk persimpangan ray-sphere dapat ditemukan di sini , saya sangat menyarankan Anda untuk melakukan ini dan memeriksa kode saya.
Bagaimana cara kerja penelusuran sinar? Ini sangat sederhana. Pada langkah pertama kita baru saja mengisi gambar dengan gradien warna:
for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } }
Sekarang untuk setiap piksel kita akan membentuk sinar yang berasal dari asal dan melewati piksel kita, dan kemudian memeriksa apakah sinar ini berpotongan dengan bola:

Jika tidak ada persimpangan dengan bola, kami menggambar piksel dengan color1, sebaliknya dengan color2:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { float sphere_dist = std::numeric_limits<float>::max(); if (!sphere.ray_intersect(orig, dir, sphere_dist)) { return Vec3f(0.2, 0.7, 0.8);
Pada titik ini, saya sarankan Anda untuk mengambil pensil dan memeriksa di atas kertas semua perhitungan (persimpangan ray-sphere dan menyapu gambar dengan sinar). Untuk jaga-jaga, kamera kami ditentukan oleh hal-hal berikut:
- lebar gambar
- tinggi gambar
- bidang sudut pandang
- lokasi kamera, Vec3f (0.0.0)
- lihat arah, sepanjang sumbu z, ke arah minus tanpa batas
Biarkan saya menggambarkan bagaimana kita menghitung arah awal sinar untuk dilacak. Pada loop utama kita memiliki rumus ini:
float x = (2*(i + 0.5)/(float)width - 1)*tan(fov/2.)*width/(float)height; float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.);
Dari mana asalnya? Cukup sederhana. Kamera kami ditempatkan di tempat asal dan menghadap ke arah -z. Biarkan saya menggambarkan hal-hal, gambar ini menunjukkan kamera dari atas, sumbu y menunjukkan layar:
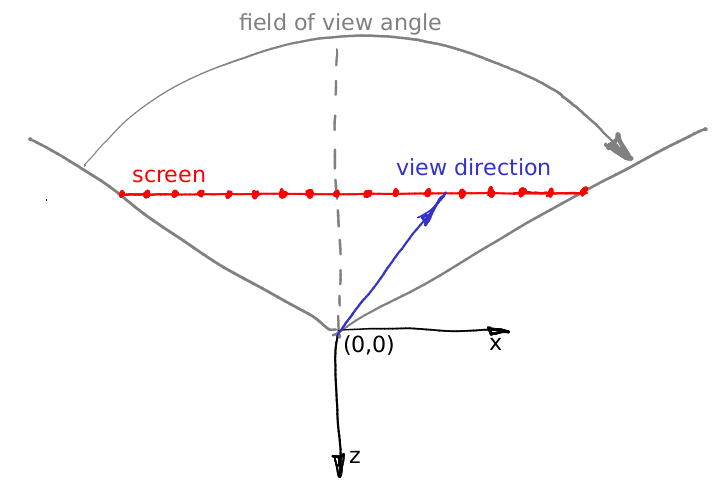
Seperti yang saya katakan, kamera ditempatkan di tempat asal, dan pemandangan diproyeksikan di layar yang terletak di bidang z = -1. Bidang pandang menentukan sektor ruang apa yang akan terlihat di layar. Dalam gambar kami layarnya 16 piksel lebar; dapatkah Anda menghitung panjangnya dalam koordinat dunia? Ini cukup sederhana: mari kita fokus pada segitiga yang dibentuk oleh garis putus-putus merah, abu-abu dan abu-abu. Sangat mudah untuk melihat tan itu (bidang pandang / 2) = (lebar layar) 0,5 / (jarak layar kamera). Kami menempatkan layar pada jarak 1 dari kamera, dengan demikian (lebar layar) = 2 tan (bidang pandang / 2).
Sekarang mari kita katakan bahwa kita ingin membuat vektor melalui tengah piksel ke-12 layar, yaitu kita ingin menghitung vektor biru. Bagaimana kita bisa melakukan itu? Berapa jarak dari kiri layar ke ujung vektor biru? Pertama-tama, itu adalah 12 + 0,5 piksel. Kita tahu bahwa 16 piksel layar sesuai dengan 2 tan (fov / 2) unit dunia. Dengan demikian, ujung vektor terletak di (12 + 0,5) / 16 2 tan (fov / 2) satuan dunia dari tepi kiri, atau pada jarak (12 + 0,5) 2/16 * tan (fov / 2) - tan (fov / 2) dari persimpangan antara layar dan sumbu -z. Tambahkan rasio aspek layar ke perhitungan dan Anda akan menemukan formula untuk arah ray.
Langkah 3: tambahkan lebih banyak bola
Bagian tersulit sudah berakhir, dan sekarang jalan kita sudah jelas. Jika kita tahu cara menggambar satu bola, kita tidak perlu waktu lama untuk menambahkan beberapa bola lagi. Periksa perubahan dalam kode, dan ini adalah gambar yang dihasilkan:

Langkah 4: pencahayaan
Gambar sempurna dalam semua aspek, kecuali kurangnya cahaya. Sepanjang sisa artikel kita akan berbicara tentang pencahayaan. Mari kita tambahkan beberapa sumber cahaya titik:
struct Light { Light(const Vec3f &p, const float &i) : position(p), intensity(i) {} Vec3f position; float intensity; };
Menghitung iluminasi global yang nyata adalah tugas yang sangat, sangat sulit, jadi seperti orang lain, kita akan menipu mata dengan menggambar sepenuhnya hasil non-fisik, tetapi masuk akal secara visual. Pertama-tama: mengapa dingin di musim dingin dan panas di musim panas? Karena pemanasan permukaan bumi tergantung pada sudut datangnya sinar matahari. Semakin tinggi matahari terbit di atas cakrawala, semakin terang permukaannya. Sebaliknya, semakin rendah di atas cakrawala, semakin redupnya. Dan setelah matahari terbenam di cakrawala, foton bahkan tidak mencapai kita sama sekali.
Kembali bola kami: kami memancarkan sinar dari kamera (tidak ada hubungannya dengan foton!) Saat itu berhenti di bola. Bagaimana kita tahu intensitas pencahayaan titik persimpangan? Bahkan, cukup untuk memeriksa sudut antara vektor normal pada titik ini dan vektor yang menggambarkan arah cahaya. Semakin kecil sudutnya, semakin baik permukaannya menyala. Ingatlah bahwa produk skalar antara dua vektor a dan b sama dengan produk norma vektor kali kosinus sudut antara vektor: a * b = | a | | b | cos (alpha (a, b)). Jika kita mengambil vektor satuan panjang, produk titik akan memberi kita intensitas pencahayaan permukaan.
Jadi, dalam fungsi cast_ray, alih-alih warna konstan, kami akan mengembalikan warna dengan mempertimbangkan sumber cahaya:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { [...] float diffuse_light_intensity = 0; for (size_t i=0; i<lights.size(); i++) { Vec3f light_dir = (lights[i].position - point).normalize(); diffuse_light_intensity += lights[i].intensity * std::max(0.f, light_dir*N); } return material.diffuse_color * diffuse_light_intensity; }
Modifikasi wrt langkah sebelumnya tersedia di sini , dan inilah hasilnya:

Langkah 5: pencahayaan specular
Trik produk titik memberikan perkiraan yang baik tentang pencahayaan permukaan matt, dalam literatur itu disebut iluminasi difus. Apa yang harus kita lakukan jika kita ingin menggambar permukaan yang mengkilap? Saya ingin mendapatkan gambar seperti ini:

Periksa seberapa sedikit modifikasi yang diperlukan. Singkatnya, semakin terang cahaya pada permukaan mengkilap, semakin sedikit sudut antara arah tampilan dan arah cahaya yang dipantulkan .
Ini tipuan dengan pencahayaan permukaan matt dan mengkilap dikenal sebagai model refleksi Phong . Wiki memiliki deskripsi yang cukup rinci tentang model pencahayaan ini. Bisa menyenangkan untuk membacanya berdampingan dengan kode sumber. Inilah gambar kunci untuk memahami keajaiban:

Langkah 6: bayangan
Mengapa kita memiliki cahaya, tetapi tidak ada bayangan? Itu tidak baik! Saya ingin gambar ini:

Hanya enam baris kode memungkinkan kami untuk mencapai ini: ketika menggambar setiap titik, kami hanya memastikan bahwa segmen antara titik saat ini dan sumber cahaya tidak memotong objek pemandangan kami. Jika ada persimpangan, kami lewati sumber cahaya saat ini. Hanya ada sedikit kehalusan: Saya mengganggu titik dengan memindahkannya ke arah normal:
Vec3f shadow_orig = light_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
Kenapa begitu? Hanya saja titik kita terletak pada permukaan objek, dan (kecuali untuk pertanyaan kesalahan numerik) sinar apa pun dari titik ini akan memotong objek itu sendiri.
Langkah 7: refleksi
Ini luar biasa, tetapi untuk menambahkan refleksi ke render kami, kami hanya perlu menambahkan tiga baris kode:
Vec3f reflect_dir = reflect(dir, N).normalize(); Vec3f reflect_orig = reflect_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
Lihat sendiri: ketika memotong bola, kami hanya menghitung sinar yang dipantulkan (dengan bantuan fungsi yang sama yang kami gunakan untuk sorotan specular!) Dan secara rekursif memanggil fungsi cast_ray ke arah sinar yang dipantulkan. Pastikan untuk bermain dengan kedalaman rekursi , saya atur ke 4, coba nilai yang berbeda pengisian dari 0, apa yang akan berubah dalam gambar? Inilah hasil saya dengan refleksi dan kedalaman rekursi 4:

Langkah 8: refraksi
Jika kita tahu melakukan refleksi, pembiasan itu mudah . Kita perlu menambahkan satu fungsi untuk menghitung sinar yang dibiaskan ( menggunakan hukum Snell ), dan tiga baris kode lainnya dalam cast_ray fungsi rekursif kami. Inilah hasil di mana bola terdekat "terbuat dari kaca", itu memantulkan dan membiaskan cahaya pada saat yang bersamaan:

Steo 9: di luar bola
Hingga saat ini kami hanya memberikan bidang karena merupakan salah satu objek matematika nontrivial yang paling sederhana. Mari kita tambahkan pesawat. Papan catur adalah pilihan klasik. Untuk tujuan ini, cukup menambahkan beberapa baris .
Dan inilah hasilnya:

Seperti yang dijanjikan, kode memiliki 256 baris kode, periksa sendiri !
Langkah 10: tugas rumah
Kami telah menempuh perjalanan panjang: kami telah belajar cara menambahkan objek ke pemandangan, cara menghitung pencahayaan yang agak rumit. Biarkan saya meninggalkan Anda dua tugas sebagai pekerjaan rumah. Benar-benar semua pekerjaan persiapan telah dilakukan dalam pekerjaan rumah cabang _ tugas . Setiap tugas akan membutuhkan sepuluh baris kode puncak.
Tugas 1: peta lingkungan
Saat ini, jika sinar tidak memotong objek apa pun, kami hanya mengatur piksel ke warna latar belakang konstan. Dan mengapa, sebenarnya, apakah itu konstan? Mari kita mengambil foto bulat (file envmap.jpg ) dan menggunakannya sebagai latar belakang! Untuk membuat hidup lebih mudah, saya menautkan proyek kami dengan perpustakaan stb untuk kenyamanan bekerja dengan format jpg. Seharusnya memberi kita gambar seperti itu:

Tugas 2: dukun!
Kita dapat membuat bola dan pesawat (lihat kotak-kotak). Jadi mari kita menggambar jerat segitiga! Saya telah menulis kode yang memungkinkan Anda membaca file .obj, dan saya telah menambahkan fungsi persimpangan ray-triangle ke dalamnya. Sekarang menambahkan bebek ke adegan kita seharusnya cukup sepele:

Kesimpulan
Tujuan utama saya adalah menunjukkan proyek yang menarik (dan mudah!) Ke program. Saya yakin bahwa untuk menjadi programmer yang baik, seseorang harus melakukan banyak proyek sampingan. Saya tidak tahu tentang Anda, tetapi saya pribadi tidak tertarik dengan perangkat lunak akuntansi dan permainan kapal penyapu ranjau, bahkan jika kompleksitas kode ini cukup sebanding.
Beberapa jam dan dua ratus lima puluh baris kode memberi kita raytracer. Lima ratus baris rasterizer perangkat lunak dapat dilakukan dalam beberapa hari. Grafik sangat keren untuk mempelajari pemrograman!