
Pada bulan Oktober, kejuaraan pemrograman kedua diadakan. Kami menerima 12.500 aplikasi, lebih dari 6.000 orang mencoba di kompetisi. Kali ini, para peserta dapat memilih salah satu lagu berikut: backend, frontend, pengembangan ponsel dan pembelajaran mesin. Di setiap trek, ia harus melewati tahap kualifikasi dan final.
Secara tradisi, kami akan menerbitkan analisis trek di Habré. Mari kita mulai dengan tugas fase kualifikasi pembelajaran mesin. Tim menyiapkan lima tugas seperti itu, di mana ada dua opsi untuk tiga tugas: di versi pertama ada tugas A1, B1 dan C, di yang kedua - A2, B2 dan C. Opsi ini didistribusikan secara acak di antara para peserta. Penulis tugas C adalah pengembang kami Pavel Parkhomenko, tugas yang tersisa dilakukan oleh rekannya Nikita Senderovich.
Untuk tugas algoritmik sederhana pertama (A1 / A2), peserta bisa mendapatkan 50 poin dengan menyebutkan jawaban dengan benar. Untuk tugas kedua (B1 / B2) kami berikan dari 10 hingga 100 poin - tergantung pada efektivitas solusi. Untuk mendapatkan 100 poin, diperlukan untuk menerapkan metode pemrograman dinamis. Tugas ketiga dikhususkan untuk membangun model klik berdasarkan pada data pelatihan yang disediakan. Untuk itu diperlukan penerapan metode untuk bekerja dengan atribut kategorikal dan penggunaan model pembelajaran non-linear (misalnya, peningkatan gradien). Untuk tugas itu memungkinkan untuk mendapatkan hingga 150 poin - tergantung pada nilai fungsi kerugian pada sampel uji.
A1. Kembalikan panjang carousel
Ketentuan
Sistem rekomendasi harus secara efektif menentukan kepentingan orang. Dan selain metode pembelajaran mesin, solusi antarmuka khusus digunakan untuk melakukan tugas ini, yang secara eksplisit menanyakan kepada pengguna apa yang menarik baginya. Salah satu solusi tersebut adalah korsel.
Korsel adalah pita kartu horizontal, yang masing-masing menawarkan berlangganan ke sumber atau topik tertentu. Kartu yang sama dapat ditemukan di korsel beberapa kali. Korsel dapat digulir dari kiri ke kanan, sedangkan setelah kartu terakhir pengguna kembali melihat yang pertama. Bagi pengguna, transisi dari kartu terakhir ke yang pertama tidak terlihat, dari sudut pandangnya rekaman itu tidak ada habisnya.
Pada titik tertentu, seorang pengguna yang penasaran Vasily memperhatikan bahwa kaset itu benar-benar dililitkan, dan memutuskan untuk mencari tahu panjang korsel yang sebenarnya. Untuk melakukan ini, ia mulai menggulir kaset dan secara berurutan menuliskan kartu rapat, untuk memudahkan, menunjuk setiap kartu dengan huruf Latin kecil. Jadi Vasily menulis kartu n pertama di selembar kertas. Dijamin bahwa dia melihat semua kartu korsel setidaknya sekali. Kemudian Vasily pergi tidur, dan di pagi hari dia menemukan bahwa seseorang telah menumpahkan segelas air pada catatannya dan sekarang beberapa surat tidak dapat dikenali.
Menurut informasi yang tersisa, bantu Vasily menentukan jumlah kartu sekecil mungkin di korsel.
Format dan Contoh I / OFormat input
Baris pertama berisi bilangan bulat tunggal n (1 ≤ n ≤ 1000) - jumlah karakter yang ditulis oleh Vasily.
Baris kedua berisi urutan yang ditulis oleh Vasily. Ini terdiri dari n karakter - huruf Latin kecil dan tanda #, yang berarti bahwa huruf pada posisi ini tidak dapat dikenali.
Format output
Cetak angka positif bilangan bulat tunggal - jumlah kartu terkecil yang ada di korsel.
Contoh 1
Contoh 2
Contoh 3
Contoh 4
Catatan
Pada contoh pertama, semua huruf dikenali, korsel minimum dapat terdiri dari 3 kartu - abc.
Pada contoh kedua, semua huruf dikenali, korsel minimum dapat terdiri dari 3 kartu - abb. Harap dicatat bahwa kartu kedua dan ketiga dalam korsel ini adalah sama.
Pada contoh ketiga, panjang korsel terkecil yang mungkin diperoleh jika kita mengasumsikan bahwa simbol a berada di posisi ketiga. Kemudian baris awal adalah ababa, korsel minimum terdiri dari 2 kartu - ab.
Pada contoh keempat, string sumber bisa berupa apa saja, misalnya ffffff. Kemudian korsel dapat terdiri dari satu kartu - f.
Sistem penilaian
Hanya setelah melewati semua tes untuk tugas itu Anda bisa mendapatkan
50 poin .
Dalam sistem pengujian, tes 1-4 adalah contoh dari kondisi tersebut.
Solusi
Cukup untuk memilah panjang korsel yang mungkin dari 1 hingga n dan untuk setiap pemeriksaan panjang tetap apakah bisa seperti itu. Jelas bahwa jawabannya selalu ada, karena nilai n dijamin menjadi kemungkinan jawaban. Untuk p panjang korsel tetap, cukup untuk memverifikasi bahwa dalam string yang ditransmisikan untuk semua i dari 0 hingga (p - 1) di semua posisi i, i + p, i + 2p, dll., Karakter atau # yang sama ditemukan. Jika setidaknya untuk beberapa i ada 2 karakter yang berbeda dari rentang dari ke z, maka korsel tidak boleh panjang p. Karena dalam kasus terburuk, untuk setiap p, Anda perlu menjalankan semua karakter string sekali, kompleksitas algoritma ini adalah O (n
2 ).
def check_character(char, curchar): return curchar is None or char == "#" or curchar == char def need_to_assign_curchar(char, curchar): return curchar is None and char != "#" n = int(input()) s = input().strip() for p in range(1, n + 1): is_ok = True for i in range(0, p): curchar = None for j in range(i, n, p): if not check_character(s[j], curchar): is_ok = False break if need_to_assign_curchar(s[j], curchar): curchar = s[j] if not is_ok: break if is_ok: print(p) break
A2. Kembalikan panjang carousel
Ketentuan
Sistem rekomendasi harus secara efektif menentukan kepentingan orang. Dan selain metode pembelajaran mesin, solusi antarmuka khusus digunakan untuk melakukan tugas ini, yang secara eksplisit menanyakan kepada pengguna apa yang menarik baginya. Salah satu solusi tersebut adalah korsel.
Korsel adalah pita kartu horizontal, yang masing-masing menawarkan berlangganan ke sumber atau topik tertentu. Kartu yang sama dapat ditemukan di korsel beberapa kali. Korsel dapat digulir dari kiri ke kanan, sedangkan setelah kartu terakhir pengguna kembali melihat yang pertama. Bagi pengguna, transisi dari kartu terakhir ke yang pertama tidak terlihat, dari sudut pandangnya rekaman itu tidak ada habisnya.
Pada titik tertentu, seorang pengguna yang ingin tahu Vasily memperhatikan bahwa rekaman itu benar-benar dililitkan, dan memutuskan untuk mencari tahu panjang korsel yang sebenarnya. Untuk melakukan ini, ia mulai menggulir kaset dan secara berurutan menuliskan kartu rapat, untuk memudahkan, menunjuk setiap kartu dengan huruf Latin kecil. Jadi Vasily menulis kartu n pertama. Dijamin bahwa dia melihat semua kartu korsel setidaknya sekali. Karena Vasily terganggu oleh isi kartu, ketika menulis, dia bisa keliru mengganti satu huruf dengan yang lain, tetapi diketahui bahwa total dia membuat tidak lebih dari k kesalahan.
Rekaman yang dibuat oleh Vasily jatuh ke tangan Anda, Anda juga tahu nilai k. Tentukan berapa sedikit kartu yang bisa berada di korselnya.
Format dan Contoh I / OFormat input
Baris pertama berisi dua bilangan bulat: n (1 ≤ n ≤ 500) - jumlah karakter yang ditulis oleh Basil, dan k (0 ≤ k ≤ n) - jumlah kesalahan maksimum yang dengan mudah dilakukan.
Baris kedua berisi n huruf kecil dari alfabet Latin - urutan yang ditulis oleh Vasily.
Format output
Cetak angka positif bilangan bulat tunggal - jumlah kartu sekecil mungkin dalam korsel.
Contoh 1
Contoh 2
Contoh 3
Contoh 4
Catatan
Pada contoh pertama, k = 0, dan kami tahu pasti bahwa Vasily tidak salah, korsel minimum dapat terdiri dari 3 kartu - abc.
Pada contoh kedua, panjang korsel terkecil yang mungkin diperoleh jika kita mengasumsikan bahwa Vasily dengan keliru mengganti huruf ketiga a dengan c. Maka garis yang sebenarnya adalah ababa, korsel minimum terdiri dari 2 kartu - ab.
Pada contoh ketiga, diketahui bahwa Vasily bisa membuat satu kesalahan. Namun, ukuran korsel minimal, dengan asumsi bahwa dia tidak melakukan kesalahan. Korsel minimum terdiri dari 3 kartu - abb. Harap dicatat bahwa kartu kedua dan ketiga dalam korsel ini adalah sama.
Pada contoh keempat, kita dapat mengatakan bahwa Vasily salah dalam memasukkan semua huruf, dan baris asli sebenarnya bisa berupa apa saja, misalnya ffffff. Kemudian korsel dapat terdiri dari satu kartu - f.
Sistem penilaian
Hanya setelah melewati semua tes untuk tugas itu Anda bisa mendapatkan
50 poin .
Dalam sistem pengujian, tes 1-4 adalah contoh dari kondisi tersebut.
Solusi
Cukup untuk memilah panjang korsel yang mungkin dari 1 hingga n dan untuk setiap pemeriksaan panjang tetap apakah bisa seperti itu. Jelas bahwa jawabannya selalu ada, karena nilai n dijamin menjadi jawaban yang mungkin, berapapun nilai k. Untuk p panjang korsel tetap, cukup untuk menghitung secara independen semua i dari 0 hingga (p - 1) berapa jumlah kesalahan minimum yang dilakukan pada posisi i, i + p, i + 2p, dll. Jumlah kesalahan ini minimal jika dianggap benar simbol adalah yang paling sering ditemukan di posisi ini. Kemudian jumlah kesalahan sama dengan jumlah posisi di mana surat lain berdiri. Jika untuk beberapa p jumlah total kesalahan tidak melebihi k, maka nilai p adalah jawaban yang mungkin. Karena untuk setiap p Anda perlu memeriksa semua karakter string sekali, kompleksitas algoritma ini adalah O (n
2 ).
n, k = map(int, input().split()) s = input().strip() for p in range(1, n + 1): mistakes = 0 for i in range(0, p): counts = [0] * 26 for j in range(i, n, p): counts[ord(s[j]) - ord("a")] += 1 mistakes += sum(counts) - max(counts) if mistakes <= k: print(p) break
B1. Rekaman rekomendasi optimal
Ketentuan
Pembentukan bagian selanjutnya dari penerbitan pribadi rekomendasi untuk pengguna bukanlah tugas yang mudah. Pertimbangkan n publikasi yang dipilih dari basis rekomendasi berdasarkan pemilihan kandidat. Nomor publikasi i ditandai dengan skor relevansi s
i dan satu set atribut k binary a
i1 , a
i2 , ..., a
ik . Setiap atribut ini sesuai dengan beberapa properti publikasi, misalnya, apakah pengguna berlangganan ke sumber publikasi ini, apakah publikasi itu dibuat dalam 24 jam terakhir, dll. Publikasi dapat memiliki beberapa properti ini sekaligus, dalam hal ini atribut yang sesuai mengambil nilai. 1, atau mungkin tidak memilikinya - dan semua atributnya adalah 0.
Agar umpan pengguna menjadi beragam, perlu untuk memilih di antara kandidat dan publikasi sehingga di antara mereka ada setidaknya publikasi A
1 yang memiliki properti pertama, setidaknya publikasi A
2 yang memiliki properti kedua, ..., publikasi yang memiliki properti dari angka k. Temukan skor relevansi total maksimum yang mungkin untuk publikasi yang memenuhi persyaratan ini, atau tentukan bahwa set publikasi seperti itu tidak ada.
Format dan Contoh I / OFormat input
Baris pertama berisi tiga bilangan bulat - n, m, k (1 ≤ n ≤ 50, 1 ≤ m ≤ min (n, 9), 1 ≤ k ≤ 5).
N baris berikutnya menunjukkan karakteristik publikasi. Publikasi ke-i diberikan integer s
i (1 ≤ s
i ≤ 10
9 ) - penilaian relevansi publikasi ini, dan kemudian ruang karakter k, yang masing-masing adalah 0 atau 1, adalah nilai dari masing-masing atribut dari publikasi ini.
Baris terakhir berisi k bilangan bulat yang dipisahkan oleh spasi - nilai A
1 , ..., A
k (0 ≤ A
i ≤ m) yang menetapkan persyaratan untuk set publikasi m terakhir.
Format output
Jika tidak ada set publikasi yang memenuhi batasan, cetak angka 0. Jika tidak, cetak angka positif bilangan bulat tunggal - skor relevansi total maksimum yang mungkin.
Contoh 1
Contoh 2
Catatan
Dalam contoh pertama, dari empat publikasi dengan dua properti, dua harus dipilih sehingga setidaknya ada satu publikasi yang memiliki properti pertama dan satu yang memiliki properti kedua. Jumlah relevansi terbesar dapat diperoleh jika kita mengambil publikasi kedua dan ketiga, meskipun opsi dengan publikasi keempat juga cocok untuk pembatasan.
Dalam contoh kedua, tidak mungkin untuk memilih dua publikasi sehingga keduanya memiliki properti kedua, karena hanya publikasi pertama yang memilikinya.
Sistem penilaian
Tes untuk tugas ini terdiri dari lima kelompok. Poin untuk masing-masing kelompok diberikan hanya ketika melewati semua tes grup dan semua tes grup
sebelumnya . Lulus tes dari kondisi diperlukan untuk mendapatkan poin untuk grup mulai dari yang kedua. Total untuk tugas Anda bisa mendapatkan
100 poin .
Dalam sistem pengujian, pengujian 1-2 adalah contoh dari kondisi tersebut.
1.
(10 poin) tes 3–10: k = 1, m ≤ 3, s
i ≤ 1000, tidak diperlukan tes dari kondisi tersebut
2.
(20 poin) menguji 11–20: k ≤ 2, m ≤ 3
3.
(20 poin) menguji 21–29: k ≤ 2
4.
(20 poin) menguji 30–37: k ≤ 3
5.
(30 poin) menguji 38–47: tidak ada batasan tambahan
Solusi
Ada n publikasi, masing-masing memiliki kecepatan dan k bendera Boolean, perlu untuk memilih kartu m sehingga jumlah relevansi maksimum dan persyaratan k dari bentuk "di antara publikasi m yang dipilih harus memiliki ≥ kartu
i dengan bendera ke-i" terpenuhi, atau menentukan bahwa set publikasi seperti itu tidak ada.
Keputusannya adalah 10 poin : jika hanya ada satu bendera, cukup untuk mengambil publikasi A
1 dengan bendera ini yang paling relevan (jika kartu kurang dari A
1 , maka set yang diinginkan tidak ada), dan sisanya (m - A
1 ) harus diambil oleh yang tersisa kartu dengan relevansi terbaik.
Solusinya adalah 30 poin : jika m tidak melebihi 3, maka Anda dapat menemukan jawabannya dengan pencarian lengkap dari semua kemungkinan O (n
3 ) tiga kali lipat kartu, pilih opsi terbaik dalam hal relevansi total yang memenuhi batasan.
Keputusannya adalah 70 poin (50 poin sama, hanya lebih mudah diimplementasikan): jika tidak ada lebih dari 3 bendera, maka Anda dapat membagi semua publikasi menjadi 8 kelompok terpisah berdasarkan kumpulan bendera yang mereka miliki: 000, 001, 010, 011, 100, 101, 110, 111. Publikasi di setiap kelompok harus disortir dalam urutan relevansi yang menurun. Kemudian, untuk O (m
4 ), kita dapat memilah-milah berapa banyak publikasi terbaik yang kita ambil dari kelompok 111, 011, 110 dan 101. Dari masing-masing kita ambil dari publikasi 0 hingga m, totalnya tidak lebih dari m. Setelah itu, menjadi jelas berapa banyak publikasi yang perlu dikumpulkan dari grup 100, 010 dan 001 untuk memenuhi persyaratan. Masih harus terbiasa dengan kartu yang tersisa dengan relevansi terbaik.
Solusi lengkap : pertimbangkan fungsi pemrograman dinamis dp [i] [a] ... [z]. Ini adalah skor total relevansi maksimum yang dapat diperoleh dengan menggunakan publikasi i persis sehingga ada publikasi dengan flag A, ..., z publikasi dengan flag Z. Kemudian, awalnya dp [0] [0] ... [0] = 0, dan untuk semua set parameter lainnya, kami menetapkan nilai sama dengan -1 untuk memaksimalkan nilai ini di masa mendatang. Selanjutnya, kita akan “masuk ke dalam permainan” kartu satu per satu dan menggunakan setiap kartu untuk meningkatkan nilai fungsi ini: untuk setiap keadaan dinamika (i, a, b, ..., z) menggunakan publikasi j-th dengan bendera (a
j , b
j , ..., z
j ), kita dapat mencoba membuat transisi ke keadaan (i + 1, a + a
j , b + b
j , ..., z + z
j ) dan memeriksa apakah hasilnya membaik di negara ini. Penting: selama transisi, kami tidak tertarik pada keadaan di mana saya ≥ m, oleh karena itu, keadaan total dinamika tersebut tidak lebih dari
mk +1 , dan perilaku asimptotik yang dihasilkan adalah O (nm
k +1 ). Ketika keadaan dinamika dihitung, jawabannya adalah keadaan yang memenuhi kendala dan memberikan skor relevansi total tertinggi.
Dari sudut pandang implementasi, sangat berguna untuk menyimpan keadaan pemrograman dinamis dan bendera dari setiap publikasi dalam bentuk yang dikemas dalam satu angka penuh untuk mempercepat pekerjaan program (lihat kode), dan tidak dalam daftar atau tupel. Solusi ini menggunakan lebih sedikit memori dan memungkinkan Anda untuk memperbarui keadaan dinamika secara efektif.
Kode Solusi Lengkap:
def pack_state(num_items, counts): result = 0 for count in counts: result = (result << 8) + count return (result << 8) + num_items def get_num_items(state): return state & 255 def get_flags_counts(state, num_flags): flags_counts = [0] * num_flags state >>= 8 for i in range(num_flags): flags_counts[num_flags - i - 1] = state & 255 state >>= 8 return flags_counts n, m, k = map(int, input().split()) scores, attributes = [], [] for i in range(n): score, flags = input().split() scores.append(int(score)) attributes.append(list(map(int, flags))) limits = list(map(int, input().split())) dp = {0 : 0} for i in range(n): score = scores[i] state_delta = pack_state(1, attributes[i]) dp_temp = {} for state, value in dp.items(): if get_num_items(state) >= m: continue new_state = state + state_delta if value + score > dp.get(new_state, -1): dp_temp[new_state] = value + score dp.update(dp_temp) best_score = 0 for state, value in dp.items(): if get_num_items(state) != m: continue flags_counts = get_flags_counts(state, k) satisfied_bounds = True for i in range(k): if flags_counts[i] < limits[i]: satisfied_bounds = False break if not satisfied_bounds: continue if value > best_score: best_score = value print(best_score)
B2. Aproksimasi fungsi
Ketentuan
Untuk menilai tingkat relevansi dokumen, berbagai metode pembelajaran mesin digunakan - misalnya, pohon keputusan. Pohon keputusan k-ary memiliki aturan keputusan di setiap node yang membagi objek ke dalam kelas k sesuai dengan nilai beberapa atribut. Dalam praktiknya, pohon keputusan biner biasanya digunakan. Pertimbangkan versi sederhana dari masalah optimisasi, yang harus diselesaikan di setiap simpul pohon keputusan k-ary.
Biarkan fungsi diskrit f didefinisikan pada titik i = 1, 2, ..., n. Hal ini diperlukan untuk menemukan fungsi konstanta piecewise g yang terdiri dari tidak lebih dari k bagian dari konstancy sehingga nilai SSE =
(g (i) - f (i))
2 minimal.
Format dan Contoh I / OFormat input
Baris pertama berisi dua bilangan bulat n dan k (1 ≤ n ≤ 300, 1 ≤ k ≤ min (n, 10)).
Baris kedua berisi n bilangan bulat f (1), f (2), ..., f (n) - nilai-nilai fungsi perkiraan pada titik 1, 2, ..., n (–10
6 ≤ f (i) ≤ 10
6 ).
Format output
Cetak satu nomor - nilai minimum yang mungkin dari SSE. Jawabannya dianggap benar jika kesalahan absolut atau relatif tidak melebihi 10
–6 .
Contoh 1
Contoh 2
Contoh 3
Catatan
Pada contoh pertama, fungsi optimal g adalah konstanta g (i) = 2.
SSE = (2 - 1)
2 + (2 - 2)
2 + (2 - 3)
2 = 2.
Dalam contoh kedua, ada 2 opsi. Baik g (1) = 1 dan g (2) = g (3) = 2.5, atau g (1) = g (2) = 1.5 dan
g (3) = 3. Dalam hal apa pun, SSE = 0,5.
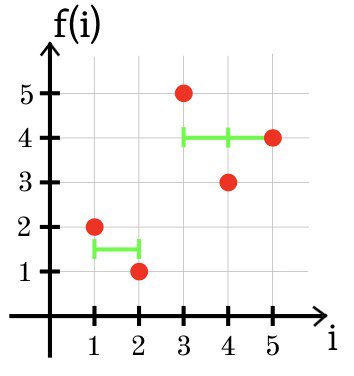
Pada contoh ketiga, perkiraan optimal dari fungsi f menggunakan dua bagian konstanta ditunjukkan di bawah ini: g (1) = g (2) = 1,5 dan g (3) = g (4) = g (5) = 4.
SSE = (1.5 + 2)
2 + (1.5 - 1)
2 + (4 - 5)
2 + (4 - 3)
2 + (4 - 4)
2 = 2.5.
Sistem penilaian
Tes untuk tugas ini terdiri dari lima kelompok. Poin untuk masing-masing kelompok diberikan hanya ketika melewati semua tes grup dan semua tes grup
sebelumnya . Lulus tes dari kondisi diperlukan untuk mendapatkan poin untuk grup mulai dari yang kedua. Total untuk tugas Anda bisa mendapatkan
100 poin .
Dalam sistem pengujian, pengujian 1-3 adalah contoh dari kondisi tersebut.
1.
(10 poin) tes 4-22: k = 1, tidak ada tes yang diperlukan dari kondisi tersebut
2.
(20 poin) menguji 23–28: k ≤ 2
3.
(20 poin) menguji 29–34: k ≤ 3
4.
(20 poin) menguji 35–40: k ≤ 4
5.
(30 poin) menguji 41–46: tidak ada batasan tambahan
Solusi
Seperti yang Anda ketahui, konstanta yang meminimalkan nilai SSE untuk sekumpulan nilai f1, f2, ...,
fn adalah rata-rata dari nilai yang tercantum di sini. Selain itu, karena mudah untuk memverifikasi dengan perhitungan sederhana, nilai SSE =
.
Keputusannya adalah 10 poin : kami hanya mempertimbangkan rata-rata semua nilai fungsi dan SSE sebagai O (n).
Keputusannya adalah 30 poin : kami memilah poin terakhir yang terkait dengan bagian pertama dari keteguhan keduanya, untuk partisi tetap kami menghitung SSE dan memilih yang optimal. Selain itu, penting untuk tidak lupa membongkar kasus ketika hanya ada satu bagian dari keteguhan. Kesulitan - O (n
2 ).
Keputusannya adalah 50 poin : kami mengurutkan batas divisi menjadi bagian-bagian dari konstancy untuk O (n
2 ), untuk partisi tetap menjadi 3 segmen, kami menghitung SSE dan memilih yang optimal. Kesulitan - O (n
3 ).
Keputusannya adalah 70 poin : kami menghitung jumlah dan jumlah kuadrat dari nilai f
i pada awalan, ini akan memungkinkan Anda untuk dengan cepat menghitung rata-rata dan SSE pada segmen mana pun. Kami mengurutkan batas partisi menjadi 4 bagian dari konstancy untuk O (n
3 ), menggunakan nilai pra-perhitungan pada awalan untuk O (1), kami menghitung SSE. Kesulitan - O (n
3 ).
Solusi lengkap : pertimbangkan fungsi pemrograman dinamis dp [s] [i]. Ini adalah nilai SSE terkecil jika kami memperkirakan nilai i pertama menggunakan segmen s. Lalu
dp [0] [0] = 0, dan untuk semua set parameter lainnya, kami menetapkan nilai sama dengan tak terhingga untuk lebih meminimalkan nilai ini. Kami akan memecahkan masalah, secara bertahap meningkatkan nilai s. Bagaimana cara menghitung dp [s] [i] jika nilai dinamika untuk semua s yang lebih kecil sudah dihitung? Cukup untuk menentukan t jumlah poin pertama yang dicakup oleh segmen (s - 1) sebelumnya, dan mengurutkan semua nilai t, dan memperkirakan poin (i - t) yang tersisa menggunakan segmen yang tersisa. Penting untuk memilih nilai terbaik t untuk SSE akhir pada poin i. Jika kita menghitung jumlah dan jumlah kuadrat dari nilai f
i pada awalan, maka perkiraan ini akan dilakukan dalam O (1), dan nilai dp [s] [i] dapat dihitung dalam O (n). Jawaban akhirnya adalah dp [k] [n]. Kompleksitas total algoritma adalah O (kn
2 ).
Kode Solusi Lengkap:
n, k = map(int, input().split()) f = list(map(float, input().split())) prefix_sum = [0.0] * (n + 1) prefix_sum_sqr = [0.0] * (n + 1) for i in range(1, n + 1): prefix_sum[i] = prefix_sum[i - 1] + f[i - 1] prefix_sum_sqr[i] = prefix_sum_sqr[i - 1] + f[i - 1] ** 2 def get_best_sse(l, r): num = r - l + 1 s_sqr = (prefix_sum[r] - prefix_sum[l - 1]) ** 2 ss = prefix_sum_sqr[r] - prefix_sum_sqr[l - 1] return ss - s_sqr / num dp_curr = [1e100] * (n + 1) dp_prev = [1e100] * (n + 1) dp_prev[0] = 0.0 for num_segments in range(1, k + 1): dp_curr[num_segments] = 0.0 for num_covered in range(num_segments + 1, n + 1): dp_curr[num_covered] = 1e100 for num_covered_previously in range(num_segments - 1, num_covered): dp_curr[num_covered] = min(dp_curr[num_covered], dp_prev[num_covered_previously] + get_best_sse(num_covered_previously + 1, num_covered)) dp_curr, dp_prev = dp_prev, dp_curr print(dp_prev[n])
C. Prediksi klik pengguna
Ketentuan
. , .
..
2 : (train.csv) (test.csv). , . :
— sample_id — id ,
— item — id ,
— publisher — id ,
— user — id ,
topic_i, weight_i — id i- ( 0 100) (i = 0, 1, 2, 3, 4),
— target — (1 — , 0 — ). .
.
, item, publisher, user, topic .
csv-, : sample_id target, sample_id — id , target — . test.csv. sample_id ( , test.csv). target 0 1.
logloss.
150 . logloss :
logloss . 2 , logloss 4 .
/train.csv:
test.csv:
:
Catatan
:
yadi.sk/d/pVna8ejcnQZK_A . , .
logloss :
EPS = 1e-4
def logloss(y_true, y_pred):
if abs (y_pred - 1) < EPS:
y_pred = 1 - EPS
if abs (y_pred) < EPS:
y_pred = EPS
return -y_true ∗ log(y_pred) - (1 - y_true) ∗ log(1 - y_pred)logloss logloss .
logloss :
def score(logloss):
if logloss > 0.5:
return 0.0
return min(150, (200 ∗ (0.5 - logloss)) ∗∗ 2) , . . , (, , , ) , — , - , .
, 100 ( 150).
— CatBoost . CatBoost ( ), . , . , -:
( ), , , , - ( ).
. , - , : FM (Factorization Machines) FFM (Field-aware Factorization Machines).
,
ML- .