Lapisan konvolusional: konvolusi cepat sesuai dengan metode Shmuel Vinograd

Pendahuluan

Artikel ini merupakan kelanjutan dari serangkaian artikel yang menggambarkan algoritma yang mendasarinya.
Synet adalah kerangka kerja untuk meluncurkan jaringan saraf pra-terlatih pada CPU.

Dalam artikel sebelumnya , saya menjelaskan metode berdasarkan perkalian matriks. Metode ini dengan upaya minimal dapat mencapai dalam banyak kasus lebih dari 80% dari maksimum teoritis. Tampaknya, yah, di mana kita bisa memperbaikinya lebih lanjut? Ternyata kamu bisa! Ada metode matematika yang dapat mengurangi jumlah operasi yang diperlukan untuk konvolusi. Kami akan membiasakan diri dengan salah satu metode ini, algoritma konvolusi dengan metode Vinograd, dalam artikel ini.


Shmuel Winograd 1936.01.04 - 2019.03.25 - seorang ilmuwan komputer Israel dan Amerika yang luar biasa, pencipta algoritma untuk perkalian matriks cepat, konvolusi dan transformasi Fourier.

Sedikit matematika

Meskipun, dalam pembelajaran mesin, konvolusi dengan inti kuadrat paling sering digunakan, untuk menyederhanakan presentasi, pertama-tama kita akan mempertimbangkan kasus satu dimensi. Misalkan kita memiliki input ukuran gambar satu dimensi $$$1 \ times4$:

$$

$$d = \ begin {bmatrix} d_0 & d_1 & d_2 & d_3 \ end {bmatrix} ^ T,$$

dan ukuran filter $$$1 \ times3$:

$$

$$g = \ begin {bmatrix} g_0 & g_1 & g_2 \ end {bmatrix} ^ T,$$

maka hasil konvolusi adalah:

$$

$$F (2,3) = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix}.$$

Ungkapan-ungkapan ini akan ditulis ulang dalam bentuk matriks:

$$

$$F (2,3) = \ begin {bmatrix} d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \ end {bmatrix} \ begin {bmatrix} g_0 \\ g_1 \\ g_2 \ end {bmatrix} = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix} = \ begin {bmatrix} m_1 + m_2 + m_3 \\ m_2 - m_3 - m_4 \ end {bmatrix}, (1)$$

di mana notasi digunakan:

$$

$$m_1 = (d_0-d_2) g_0, \\ m_2 = (d_1 + d_2) \ frac {g_0 + g_1 + g_2} {2}, \\ m_3 = (d_2-d_1) \ frac {g_0-g_1 + g_2} {2}, \\ m_4 = (d_1-d_3) g_2.$$

Pada pandangan pertama, penggantian terakhir terlihat agak sia-sia - jelas ada lebih banyak operasi. Tapi ekspresi $$$\ frac {g_0 + g_1 + g_2} {2}$dan $$$\ frac {g_0-g_1 + g_2} {2}$hanya perlu dihitung sekali. Dengan mengingat hal ini, kita hanya perlu melakukan 4 operasi perkalian, sedangkan dalam rumus asli mereka harus dilakukan 6.
Kami menulis ulang ekspresi (1):

$$

$$F (2,3) = A ^ T [(G g) \ odot (B ^ T d)], (2)$$

dimana $$$\ odot$menunjukkan penggandaan elemen-bijaksana, dan notasi berikut juga digunakan:

$$

$$B ^ T = \ begin {bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1 \ end { bmatrix}, (3) \\ G = \ begin {bmatrix} 1 & 0 & 0 \\ \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {2} \\ \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {2} \\ 0 & 0 & 1 \ end {bmatrix}, (4) \\ A ^ T = \ mulai {bmatrix} 1 & 1 & 1 & 0 \\ 0 & 1 & -1 & -1 \ end {bmatrix}. (5)$$

Ekspresi (2) dapat digeneralisasi ke kasus dua dimensi:

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[Gg G ^ T] \ odot [B ^ T d B] \ bigg] A. (6)$$

Jumlah operasi penggandaan yang diperlukan untuk $$$F (2 \ times2,3 \ times3)$menyusut dari $$$2 \ times2 \ times3 \ times3 = 36$sebelumnya $$$4 \ times4 = 16$. Jadi kami mendapatkan keuntungan komputasi di $$$\ frac {36} {16} = $ 2.2$kali. Jika kita memvisualisasikan, maka sebenarnya kita, alih-alih secara terpisah menghitung lilitan untuk setiap titik gambar, kami akan segera menghitungnya untuk blok ukuran $$$2 \ times2$:

Dalam hal apapun, untuk berbelit-belit dengan jendela $$$r \ kali s$dan ukuran blok $$$m \ kali n$jumlah perkalian yang dibutuhkan akan

$$

$$count = (m + r - 1) \ kali (n + s - 1), (7)$$

dan gain dijelaskan oleh rumus:

$$

$$k = \ frac {m \ kali n \ kali r \ kali s} {(m + r - 1) \ kali (n + s - 1)}. (8)$$

Dalam batas, cukup besar $$$m$dan $$$n$untuk konvolusi apa pun, hanya 1 operasi perkalian pada satu titik sudah cukup! Sayangnya, peningkatan ukuran blok menyebabkan peningkatan input overhead yang cepat $$$B ^ T d B$dan akhir pekan $$$A ^ T [...] A$gambar, jadi dalam prakteknya biasanya tidak menggunakan ukuran blok lebih besar dari $$$4 \ times4$.

Contoh implementasi

Untuk implementasi praktis dari algoritma Vinograd, saya ingin mempertimbangkan kasus paling sederhana - konvolusi dengan kernel $$$3 \ times3$untuk blok $$$2 \ times2$. Untuk lebih menyederhanakan presentasi, kami juga akan menganggap bahwa tidak ada padding gambar input, dan ukuran gambar input dan output adalah kelipatan 2.

Implementasi konvolusi berdasarkan perkalian matriks akan terlihat seperti:

float relu(float value) { return value > 0 ? return value : 0; } void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; for (int sc = 0; sc < srcC; ++sc) for (int ky = 0; ky < kernelY; ++ky) for (int kx = 0; kx < kernelX; ++kx) for (int dy = 0; dy < dstH; ++dy) for (int dx = 0; dx < dstW; ++dx) *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx]; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int M = dstC; int N = dstH * dstW; int K = srcC * kernelY * kernelX; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf); gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Mereka yang ingin memahami secara rinci apa yang terjadi di sini harus beralih ke artikel saya sebelumnya . Implementasi saat ini diperoleh dari yang sebelumnya, jika kita menempatkan:

 strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0. 

Algoritma konvolusi yang dimodifikasi

Saya berikan di sini lagi rumus (6):

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[Gg G ^ T] \ odot [B ^ T d B] \ bigg] A.$$

Jika Anda beralih dari ukuran gambar output $$$2 \ times2$ke gambar ukuran sewenang-wenang, maka kita harus memecahnya menjadi blok ukuran $$$2 \ times2$. Untuk setiap blok tersebut, gambar input akan dibentuk $$$(2 + 3 - 1) \ kali (2 + 3 - 1) = $ 1$nilai-nilai yang termasuk dalam 16 dikonversi $$$B ^ T d B$input gambar dikurangi setengahnya. Kemudian, masing-masing dari 16 matriks ini dikalikan dengan matriks yang sesuai dari bobot yang diubah $$$G g G ^ T$. 16 matriks yang dihasilkan dikonversi ke gambar output $$$A ^ T \ bigg [... \ bigg] A$. Di bawah proses ini digambarkan dalam diagram:



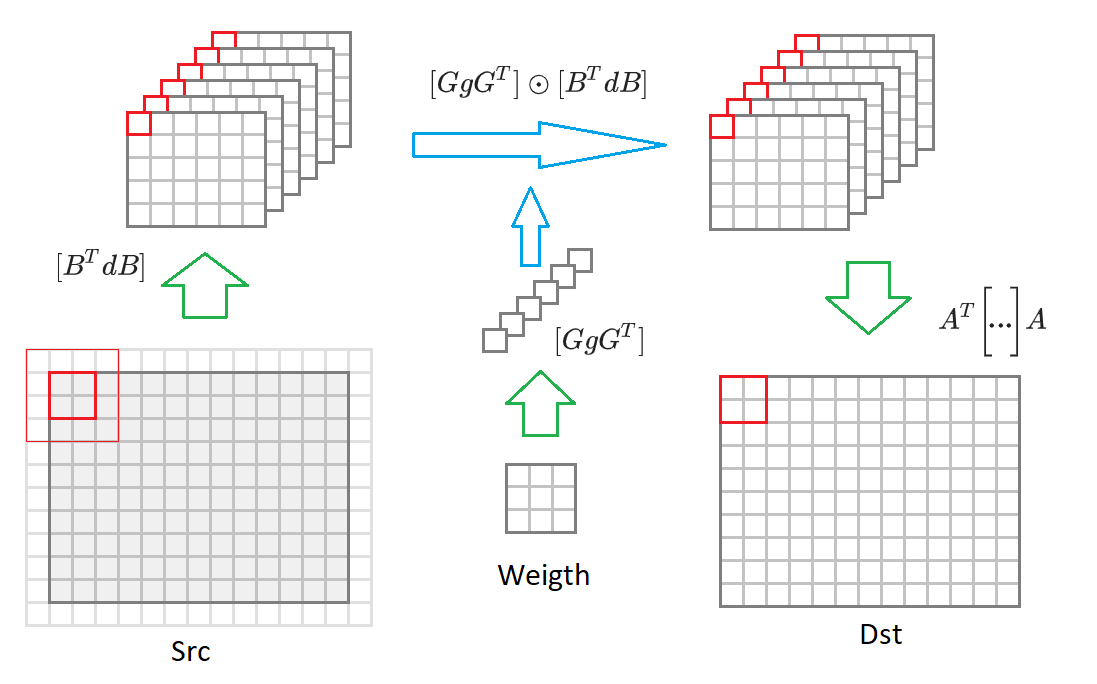
Dengan komentar ini, algoritma konvolusi berbentuk:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { const int block = 2, kernel = 3; int count = (block + kernel - 1)*(block + kernel - 1); // 16 int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int tileH = dstH / block; int tileW = dstW / block; int sizeW = srcC * dstC; int sizeS = srcC * tileH * tileW; int sizeD = dstC * tileH * tileW; int M = dstC; int N = tileH * tileW; int K = srcC; float * bufW = buf; float * bufS = bufW + sizeW*count; float * bufD = bufS + sizeS*count; set_filter(weight, sizeW, bufW); for (int b = 0; b < batch; ++b) { set_input(src, srcC, srcH, srcW, bufS, sizeS); for (int i = 0; i < count; ++i) gemm_nn(M, N, K, 1, bufW + i * sizeW, K, bufS + i * sizeS, N, 0, bufD + i * sizeD, N)); set_output(bufD, sizeD, dst, dstC, dstH, dstW); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Jumlah operasi yang diperlukan tanpa memperhitungkan transformasi akun dari input dan output gambar: ~ srcC * dstC * dstH * dstW * dihitung . Selanjutnya, kami menjelaskan algoritma untuk mengkonversi bobot, input dan output gambar.

Konversikan skala convolutional

Seperti yang dapat dilihat dari ekspresi (6), transformasi berikut harus dilakukan pada bobot konvolusi: $$$G g G ^ T$dimana matriksnya $$$G$didefinisikan dalam ekspresi (4). Kode untuk konversi ini akan terlihat seperti ini:

 void set_filter(const float * src, int size, float * dst) { for (int i = 0; i < size; i += 1, src += 9, dst += 1) { dst[0 * size] = src[0]; dst[1 * size] = (src[0] + src[2] + src[1])/2; dst[2 * size] = (src[0] + src[2] - src[1])/2; dst[3 * size] = src[2]; dst[4 * size] = (src[0] + src[6] + src[3])/2; dst[5 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4; dst[6 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4; dst[7 * size] = (src[2] + src[8] + src[5])/2; dst[8 * size] = (src[0] + src[6] - src[3])/2; dst[9 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4; dst[10 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4; dst[11 * size] = (src[2] + src[8] - src[5])/2; dst[12 * size] = src[6]; dst[13 * size] = (src[6] + src[8] + src[7])/2; dst[14 * size] = (src[6] + src[8] - src[7])/2; dst[15 * size] = src[8]; } } 

Untungnya, konversi ini perlu dilakukan hanya 1 kali. Oleh karena itu, itu tidak mempengaruhi kinerja akhir.

Input Konversi Gambar

Seperti yang dapat dilihat dari ekspresi (6), transformasi berikut harus dilakukan pada gambar input: $$$B ^ T d B$dimana matriksnya $$$B ^ T$didefinisikan dalam ekspresi (3). Kode untuk konversi ini akan terlihat seperti ini:

 void set_input(const float * src, int srcC, int srcH, int srcW, float * dst, int size) { int dstH = srcH - 2; int dstW = srcW - 2; for (int c = 0; c < srcC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[16]; for (int r = 0; r < 4; ++r) for (int c = c; c < 4; ++c) tmp[r * 4 + c] = src[(row + r) * srcW + col + c]; dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]); dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]); dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]); dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]); dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]); dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]); dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]); dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]); dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]); dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]); dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]); dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]); dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]); dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]); dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]); dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]); dst++; } } src += srcW * srcH; } } 

Jumlah operasi yang diperlukan untuk konversi ini adalah: ~ srcH * srcW * srcC * count .

Keluarkan Konversi Gambar

Seperti yang dapat dilihat dari ekspresi (6), transformasi berikut harus dilakukan pada gambar output: $$$A ^ T [...] A$dimana matriksnya $$$B ^ T$didefinisikan dalam ekspresi (5). Kode untuk konversi ini akan terlihat seperti ini:

 void set_output(const float * src, int size, float * dst, int dstC, int dstH, int dstW) { for (int c = 0; c < dstC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[8]; tmp[0] = src[0 * size] + src[1 * size] + src[2 * size]; tmp[1] = src[1 * size] - src[2 * size] - src[3 * size]; tmp[2] = src[4 * size] + src[5 * size] + src[6 * size]; tmp[3] = src[5 * size] - src[6 * size] - src[7 * size]; tmp[4] = src[8 * size] + src[9 * size] + src[10 * size]; tmp[5] = src[9 * size] - src[10 * size] - src[11 * size]; tmp[6] = src[12 * size] + src[13 * size] + src[14 * size]; tmp[7] = src[13 * size] - src[14 * size] - src[15 * size]; dst[col + 0] = tmp[0] + tmp[2] + tmp[4]; dst[col + 1] = tmp[1] + tmp[3] + tmp[5]; dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6]; dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7]; src++; } dst += 2*dstW; } } } 

Jumlah operasi yang diperlukan untuk konversi ini adalah: ~ dstH * dstW * dstC * count .

Fitur implementasi praktis

Dalam contoh di atas, kami menggambarkan algoritma Vinohrad untuk ukuran blok $$$2 \ times2$. Dalam praktiknya, versi algoritma yang lebih maju paling sering digunakan: $$$F (4 \ times4,3 \ times3)$. Dalam hal ini, ukuran blok akan menjadi $$$4 \ times4$, dan jumlah matriks yang ditransformasikan adalah 36. Keuntungan komputasi, sesuai dengan rumus (8), akan mencapai 4 . Skema umum dari algoritma adalah sama, hanya matriks dari algoritma transformasi yang berbeda.

Ada proyek kecil di Github yang memungkinkan Anda menghitung matriks ini dengan koefisien untuk ukuran kernel konvolusi dan ukuran blok yang berubah-ubah.

Kami menyajikan varian dari algoritma Vinograd untuk format gambar NCHW , tetapi algoritma tersebut dapat diimplementasikan dengan cara yang sama untuk format NHWC (saya berbicara lebih detail tentang format gambar ini di artikel sebelumnya .

Terlepas dari adanya transformasi tambahan, beban komputasi utama dalam algoritma Vinograd (tentu saja dengan aplikasi kompetennya) masih terletak pada perkalian matriks. Untungnya, ini adalah operasi standar dan diterapkan secara efektif di banyak perpustakaan.

Fungsi transformasi yang dioptimalkan untuk berbagai platform untuk algoritma Vinohrad dapat ditemukan di sini .

Pro dan Kontra dari Algoritma Grape

Pertama, tentu saja, pro:

• Algoritme memungkinkan beberapa kali (paling sering 2-3 kali) untuk mempercepat perhitungan konvolusi. Dengan demikian, adalah mungkin untuk menghitung konvolusi lebih cepat daripada batas "teoritis".
• Algoritme bergantung pada implementasinya pada algoritma multiplikasi matriks standar.
• Ini dapat diimplementasikan untuk berbagai format gambar input: NCHW , NHWC .
• Ukuran buffer untuk menyimpan nilai-nilai perantara lebih kecil dari yang dibutuhkan untuk algoritma perkalian matriks.

Nah dan di mana tanpa minus:

• Algoritme membutuhkan implementasi yang terpisah dari fungsi konversi untuk setiap ukuran kernel konvolusi, serta untuk setiap ukuran blok. Mungkin ini adalah salah satu alasan utama hampir di semua tempat hanya diterapkan untuk konvolusi dengan kernel. $$$3 \ times3$.
• Saat ukuran blok bertambah, kompleksitas penerapan fungsi konversi tumbuh dengan cepat. Oleh karena itu, praktis tidak ada implementasi dengan ukuran blok lebih besar dari $$$4 \ times4$.
• Algoritma memberlakukan batasan ketat pada parameter konvolusi strideY = strideY = dilationY = dilationX = group = 1 . Meskipun secara teoritis, dimungkinkan untuk mengimplementasikan algoritma ketika pembatasan ini dilanggar, dalam praktiknya itu kecil berlaku karena efisiensi yang rendah.
• Efisiensi algoritma berkurang jika jumlah saluran input atau output dalam gambar kecil (ini disebabkan oleh biaya konversi gambar input dan output).
• Efisiensi algoritma berkurang untuk ukuran kecil dari gambar input (matriks yang dihasilkan dari gambar input terlalu kecil, dan algoritma penggandaan matriks standar menjadi tidak efektif untuk mereka).

Kesimpulan

Metode perhitungan konvolusi berdasarkan algoritma Vinograd dapat secara signifikan meningkatkan efisiensi komputasi dibandingkan dengan metode yang didasarkan pada perkalian matriks sederhana. Sayangnya, ini tidak universal dan cukup sulit untuk diterapkan. Untuk sejumlah kasus khusus, ada pendekatan yang lebih cepat, uraian yang ingin saya tunda untuk artikel selanjutnya dari seri ini. Menunggu umpan balik dan komentar dari pembaca. Saya harap Anda tertarik!

PS Ini dan pendekatan lainnya diterapkan oleh saya dalam Kerangka Konvolusi sebagai bagian dari perpustakaan Simd .
Kerangka kerja ini mendasari Synet , kerangka kerja untuk menjalankan jaringan saraf pra-terlatih pada CPU.