Bayangkan Anda dikelilingi oleh tembok yang tinggi tak terhingga, tetapi sama sekali tidak ada yang diketahui tentang apa yang ada di balik tembok itu. Sekarang bayangkan bahwa personifikasi tembok ini adalah persamaan ini:
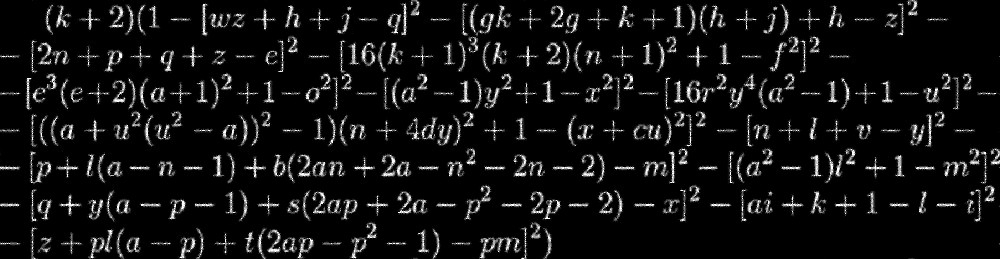
Metafora ini akan lebih mudah dipahami jika kita menggambar analogi dengan lubang hitam: kita tidak tahu apa yang ada di bawah cakrawala peristiwa, dan untuk mengetahui kita perlu menemukan cara untuk sampai ke sana. Sesuatu yang serupa ada di dunia matematika. Persamaan ini adalah "formula" nyata dari bilangan prima, tetapi untuk menggunakannya, kita perlu mencari cara mencari yang cocok
{a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, w, v, x, y, z} .
Lubang hitam dan persamaan ini adalah kondisi pamungkas dari sesuatu yang nyata dan abstrak. Dan, jika ada cukup tebakan dan gagasan tentang yang pertama, maka tentang yang kedua, praktis tidak ada yang diketahui. Tapi, bagaimana jika itu benar-benar lubang hitam "matematika"? Tidakkah kamu penasaran apa yang akan terjadi jika kita jatuh di bawah cakrawala?
Terdiri dari apa tembok itu?
Bilangan - mereka tidak ada di dunia nyata. Ada tujuh dadu, tujuh atom, tujuh dosa mematikan, tetapi ketujuh itu sendiri tidak ada - itu adalah abstraksi. Ya, kita dapat mengatakan bahwa angka hanyalah banyak objek abstrak, namun, ini adalah seluruh dunia. Dunia di mana, seperti di dunia nyata, ada hukum. Pemikiran ini sangat aneh. Namun demikian, keberadaan cabang matematika seperti teori bilangan menunjukkan bahwa "keanehan" ini sangat penting bagi kita.
Hal yang paling menarik adalah di antara objek imajiner ini ada yang spesial - bilangan prima. Mereka seperti kekacauan deterministik - dapat diprediksi dan tidak dapat diprediksi pada saat yang sama, tergantung pada skala pertimbangan mereka. Misalnya, berada di sebelah mereka, kita dapat melihat bahwa jumlah mereka di depan beberapa nomor arbitrer n tidak akan melebihi:
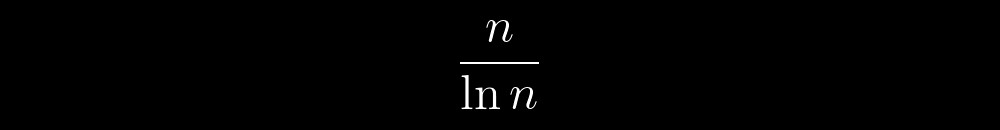
Mengubah skala, kita mulai memperhatikan banyak petunjuk tentang semacam aturan internal perilaku mereka. Secara bertahap, petunjuk ini menjadi terlalu banyak. Semakin sering pertanyaan "Dari mana asalnya?", "Bagaimana jika ada algoritma tertentu untuk mendapatkan bilangan prima?", "Bagaimana jika setiap bilangan prima dapat diperoleh dengan menggunakan algoritma yang sama?"
Bagaimana dinding itu muncul
Jika urutan angka tertentu diperoleh sebagai hasil dari operasi algoritma tertentu, maka himpunan angka dalam urutan ini dianggap dapat dihitung, meskipun itu bisa sangat besar. Set yang disebutkan memiliki satu sifat yang luar biasa - Diophantine. Ini berarti bahwa setiap rangkaian tersebut dapat diwakili oleh persamaan Diophantine - polinomial dengan koefisien dan kekuatan positif bilangan bulat.
Pernyataan berikut mungkin tampak sepenuhnya tidak masuk akal, tetapi berdasarkan definisi ini, kami dapat menyatakan bahwa semua kunci keamanan dan nilai fungsi hash (bahkan bitcoin) dapat diekspresikan melalui persamaan Diophantine. yaitu persamaan yang diselesaikan dalam bilangan bulat. Dan ya, secara teoritis, seseorang dapat mempelajari rahasia apa pun, menjadi orang yang kaya dan kuat tanpa batas. Tetapi, untuk menjadi orang seperti itu, persamaan ini pertama-tama harus disimpulkan, dan kemudian diselesaikan.
Komputer dapat mengatasi tugas merepresentasikan set oleh persamaan Diophantine, sebagian atau seluruhnya. Tetapi di sini muncul masalah lain - persamaan Diophantine tidak terpecahkan dalam bentuk umum, mis. tidak ada algoritma tunggal untuk menyelesaikannya. Ini tampaknya tidak menjadi masalah besar, karena kita tahu bahwa beberapa persamaan dibedakan menjadi bentuk yang terpisah, untuk solusi yang telah ditemukan metode yang efektif.
Tetapi meskipun ada metode ini, kami menghadapi kesulitan komputasi yang terkait dengan akurasi perhitungan atau dengan kecepatan iterasi.
Bagaimana bisa terjadi bahwa bilangan prima dapat dihitung? Proses menciptakan persamaan yang mewakili set enumerable bergantung pada dasar matematika - aritmatika dan logika. Dan jika kita memiliki pengetahuan yang cukup tentang sifat-sifat objek set tertentu, maka, berdasarkan pengetahuan ini, kita dapat membuat asumsi tentang algoritma yang memungkinkan mereka diperoleh. Dan, ternyata, pengetahuan tentang sifat-sifat bilangan prima terakumulasi cukup untuk tujuan ini. Persamaan telah diperoleh, dan sekarang semua pertanyaan yang terkait dengan bilangan prima dikurangi menjadi itu saja.
Tetapi kita tidak bisa menyelesaikannya.
Ketebalan dan kekuatan dinding
Faktanya, kita ditantang. Dan kita tahu sebelumnya tentang kekalahan yang tak terhindarkan. Mungkin retret akan menjadi keputusan yang paling bijaksana. Tetapi bukankah kita membutuhkan kekalahan ini untuk melampaui diri kita sendiri? Mari kita coba menyelesaikannya sedikit saja.
Lihatlah persamaannya lagi:
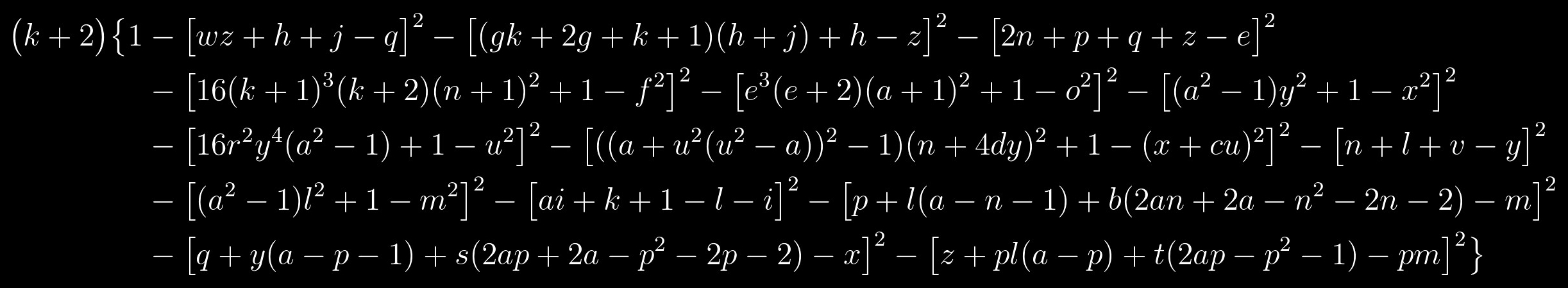
Ini adalah polinomial yang himpunan nilai positifnya bertepatan dengan himpunan bilangan prima. Ini terdiri dari dua faktor: faktor kiri akan menjadi prima hanya ketika faktor kanan, ditunjukkan oleh kurung keriting, sama dengan satu, dan ini, pada gilirannya, hanya mungkin jika setiap istilah dalam faktor ini, ditunjukkan oleh kurung siku, sama dengan nol . Ternyata pertanyaan pemecahan persamaan ini berkurang menjadi pemecahan sistem persamaan berikut:
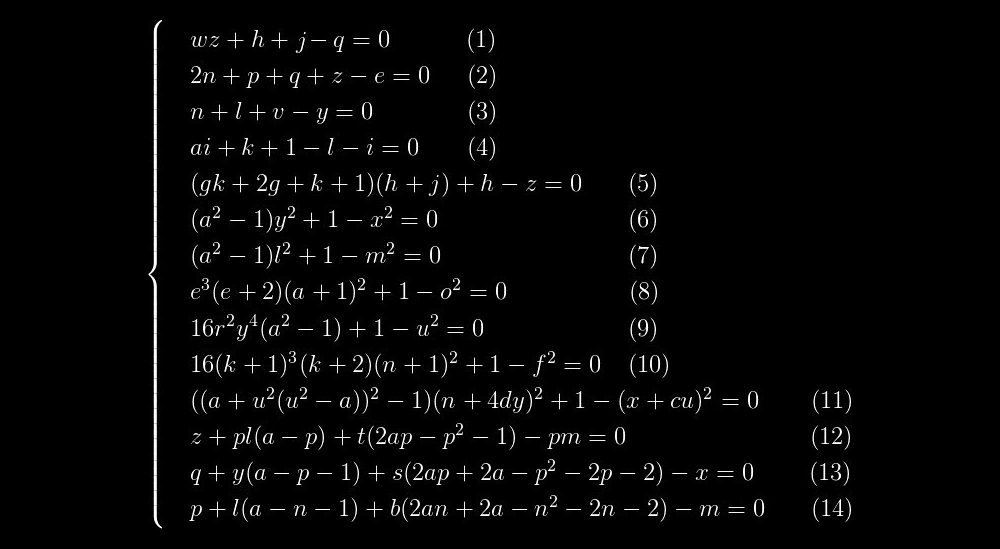
Jika kita menyelesaikan sistem persamaan ini dan menambahkan 2 ke nilai
k yang ditemukan , maka kita mendapatkan bilangan prima. Tapi kita bisa pergi ke arah lain. Ambil beberapa bilangan prima, kurangi 2 dari itu, sehingga memperoleh nilai
k , lalu gantilah nilai ini ke dalam sistem dan cobalah untuk menemukan nilai-nilai variabel yang tersisa relatif terhadapnya. Dengan cara ini kita akan pergi - cobalah untuk menemukan setidaknya satu solusi untuk polinomial ini.
Semua variabel tunduk pada dua batasan ketat, mereka harus bilangan bulat dan tidak boleh negatif. Jika kita mengambil
k = 0 , maka bilangan prima pertama yang bisa kita dapatkan adalah 2. Ini akan menjadi titik awal kita. Setelah mengganti nilai ini ke dalam sistem persamaan, ia akan mengambil bentuk berikut:
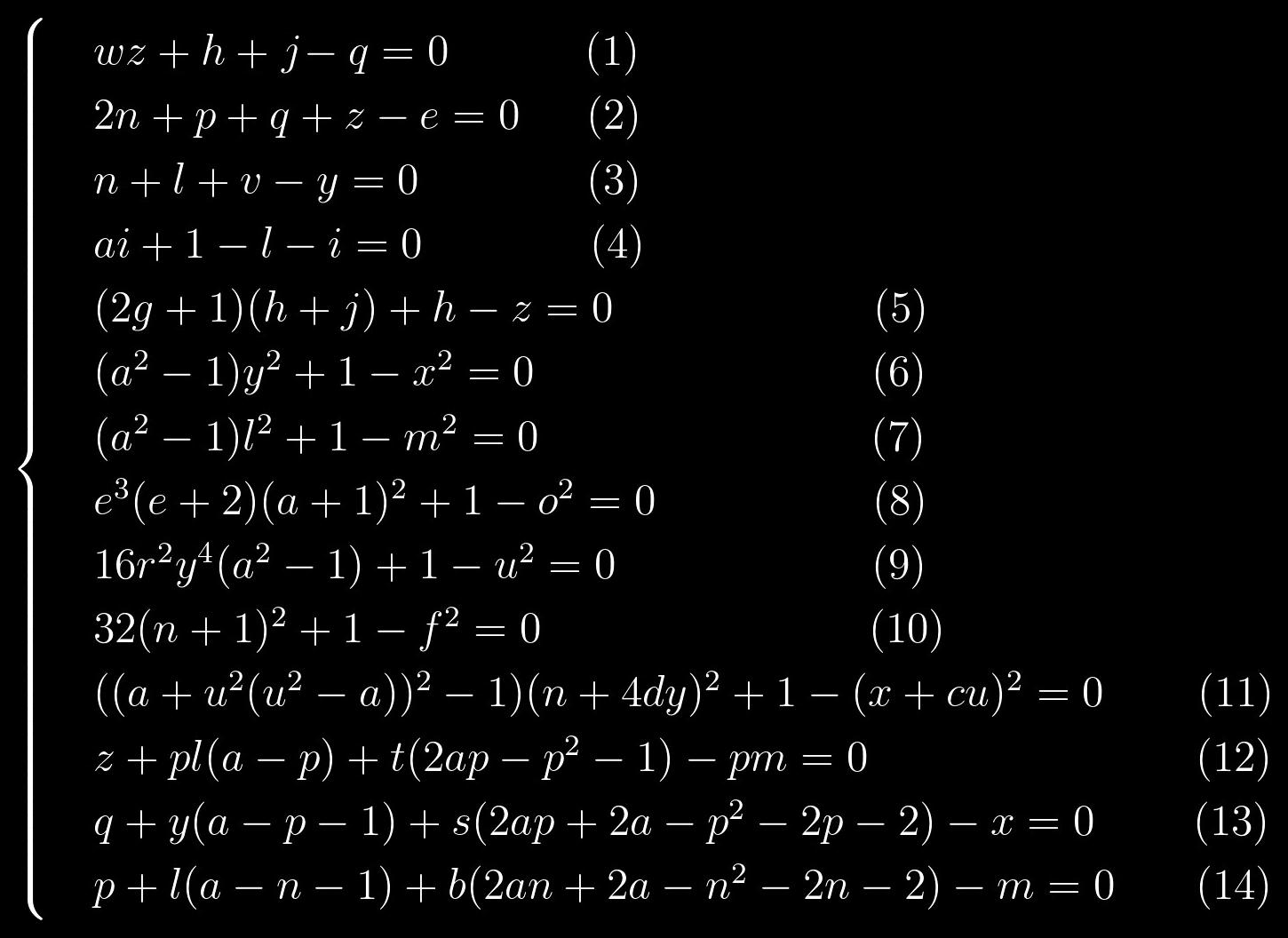
Persamaan (1) - (5) adalah persamaan linear, yaitu derajat semua variabel adalah 1. Persamaan (6) - (11) memiliki struktur yang sangat mirip. Dan akhirnya, persamaan (12) - (14) juga menonjol dalam kelompok yang terpisah, dan persamaan (13) dan (14) mirip satu sama lain, seperti dua tetes air.
Kita dapat menyingkirkan variabel, atau menurunkan derajat, tetapi kita telah melakukan ini sebelumnya. Penurunan jumlah variabel mengarah ke peningkatan kuat dalam derajat variabel lain, dan penurunan derajat variabel hanya mungkin melalui peningkatan jumlah mereka. Jadi mari kita coba selesaikan sistem ini dalam formulir ini.
Persamaan (6) - (11) adalah modifikasi dari persamaan Pell:
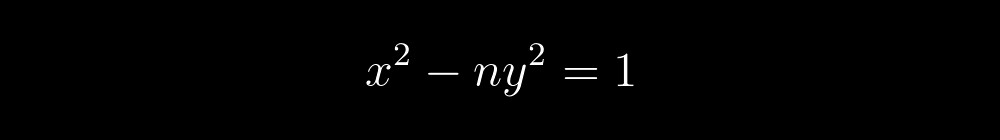
Bahkan, jika Anda menulis ulang mereka seperti ini:
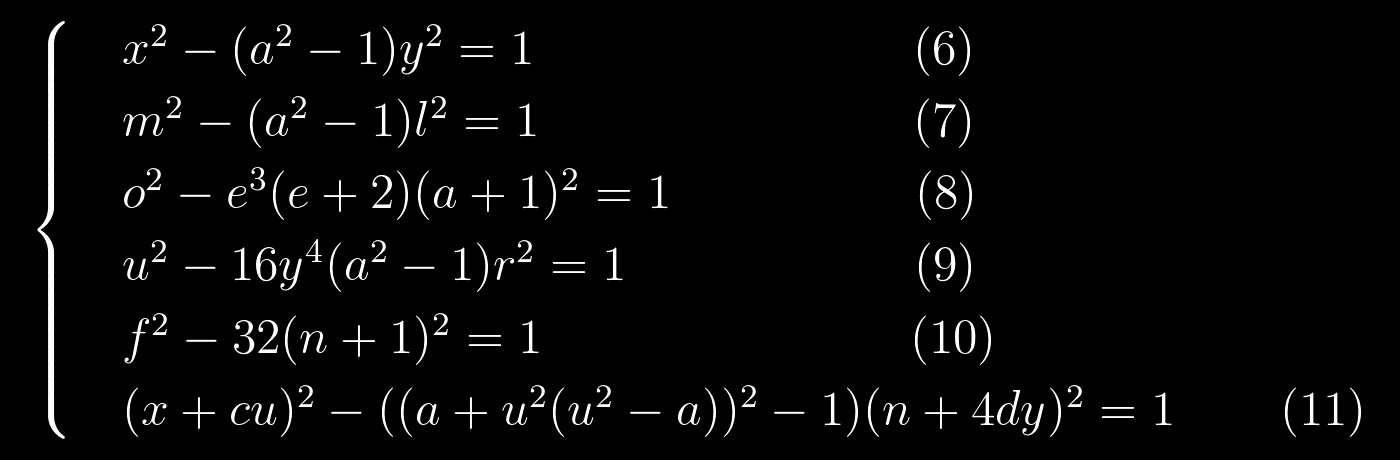
maka kesamaan menjadi jelas. Ini sangat menggembirakan, karena kita dapat menyelesaikan persamaan Pell dengan cukup baik. Kita dapat mencoba menyelesaikan sistem ini seperti ini: pertama kita menyelesaikan satu persamaan, mengganti solusinya dengan yang lain, yang juga kita selesaikan, dan seterusnya, sampai akhir. Kedengarannya cukup sederhana, tetapi tidak ada salahnya untuk menggambar sesuatu seperti grafik permutasi untuk setidaknya secara kasar mengetahui di mana untuk menyelesaikan persamaan:
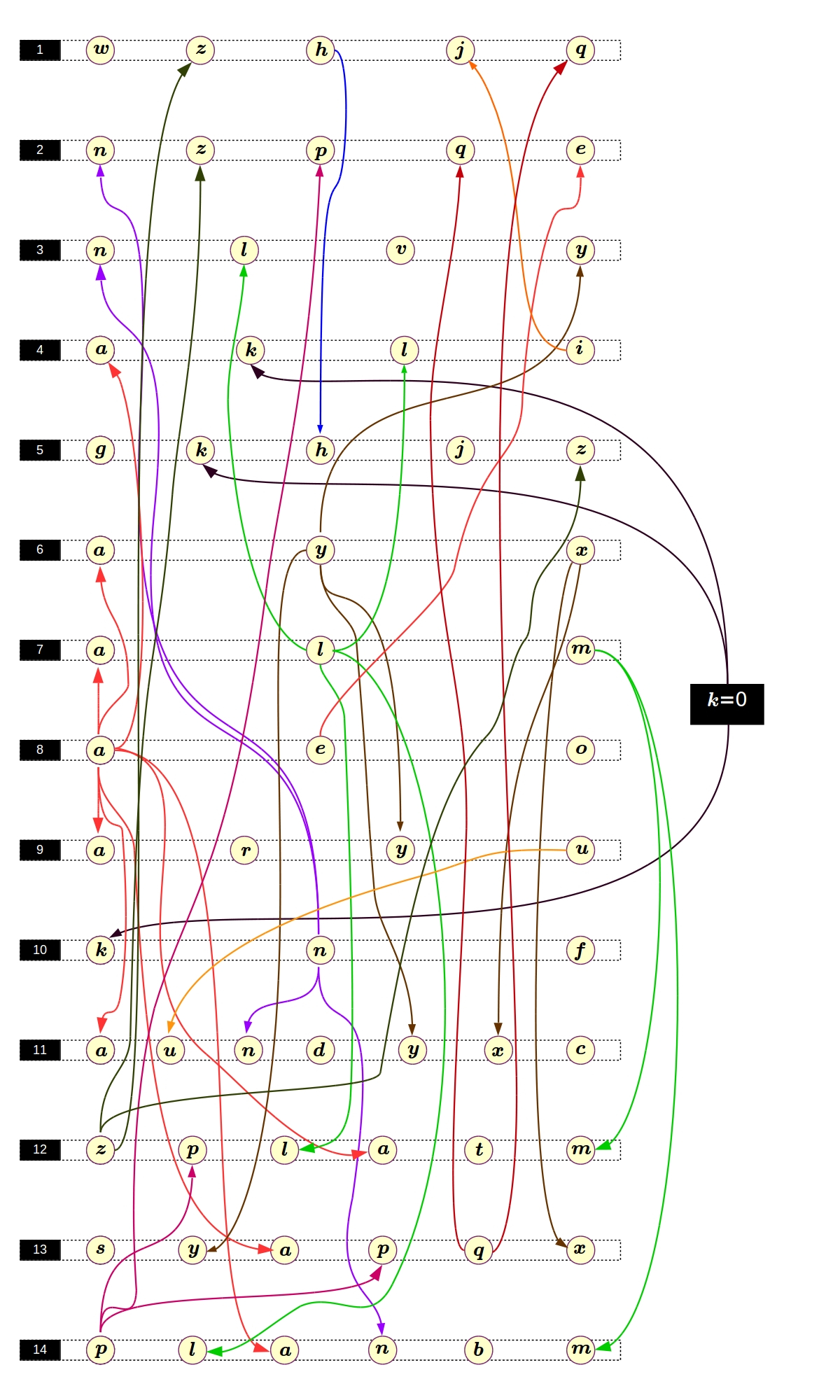
Tampaknya semuanya sederhana.
Tendangan di dinding
Kita mulai dengan persamaan Pell. Untuk menyelesaikannya, kami akan menulis skrip kecil:
from decimal import * getcontext().prec = 50 def peq_dec(N): n = Decimal(N).sqrt() a = int(n) x = n - a p0, q0 = 1, 0 p1, q1 = int(a), 1 while True: a = int(1/x) x = 1/x - a p_i = a*p1 + p0 q_i = a*q1 + q0 if p_i**2 - N*q_i**2 == 1: return p_i, q_i break p0, q0 = p1, q1 p1, q1 = p_i, q_i
Berkat dia, kita dapat segera menemukan solusi untuk persamaan (10)
n = 2 ,
f = 17 . Namun, sebelum melanjutkan, kita perlu tahu sesuatu tentang persamaan Pell.
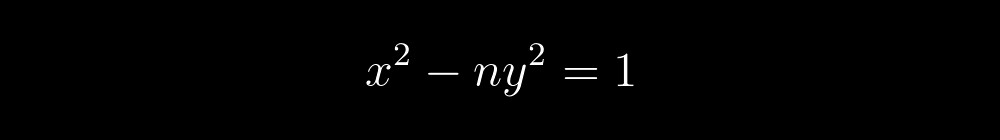
Untuk memulainya,
n tidak boleh berbentuk persegi penuh. Selain itu, setiap persamaan Pell memiliki jumlah solusi yang tak terbatas, di antaranya selalu ada yang sepele:
x = 1 dan
y = 0 . Setiap keputusan selanjutnya dapat diperoleh atas dasar keputusan sebelumnya, sesuai dengan rumus perulangan berikut:
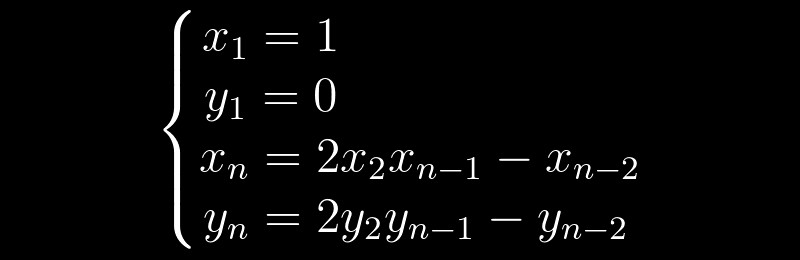
Ternyata itu cukup bagi kita untuk menemukan solusi minimal non-sepele, dan kita bisa mendapatkan sisanya menggunakan algoritma sederhana. Misalnya, untuk
n = 2, kita dapat dengan mudah menemukan solusi seperti itu, yaitu
x = 3 dan
y = 2 , maka solusi selanjutnya akan terlihat seperti ini:
17, 12 99, 70 577, 408 3363, 2378 19601, 13860 114243, 80782 665857, 470832 3880899, 2744210 22619537, 15994428 131836323, 93222358 768398401, 543339720 4478554083, 3166815962 26102926097, 18457556052 152139002499, 107578520350 886731088897, 627013566048
Apakah layak melanjutkan keputusan selanjutnya? Tentu saja itu sepadan, tetapi ... kita dapat mencoba memprediksi apa yang ada di depan.
Mari kita bayangkan sekarang bahwa kita sedang memecahkan sistem persamaan tiga persamaan Pell dari bentuk berikut:
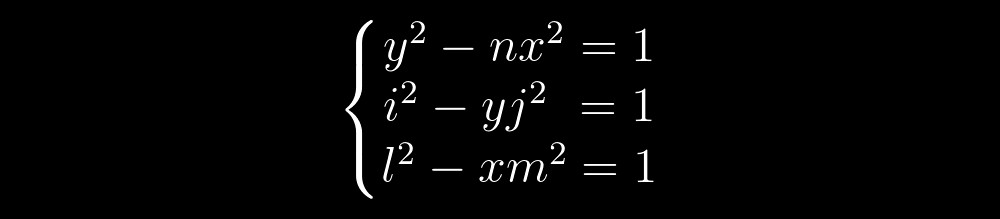
Solusi untuk persamaan Pell adalah titik hiperbola dengan koordinat bilangan bulat. Lalu, kita bisa membayangkan solusi untuk dua persamaan pertama seperti ini:
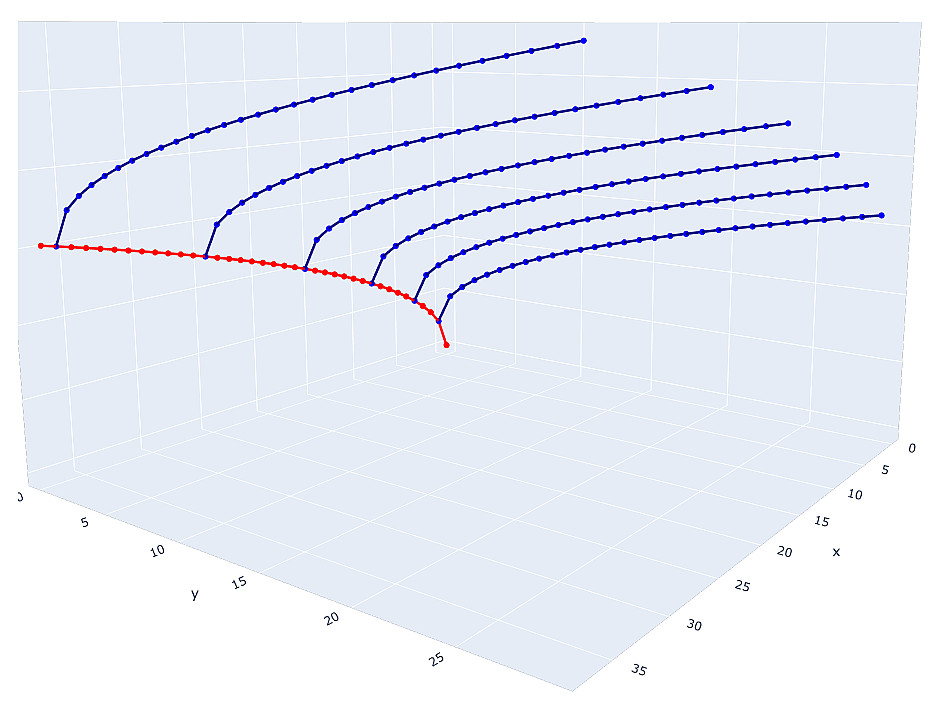
Solusi untuk persamaan pertama adalah titik integer dari hiperbola merah, tetapi koordinat
y dari setiap titik tersebut hadir dalam persamaan kedua dan dapat menghasilkan hiperbola biru yang titik integernya akan menjadi solusi untuk persamaan kedua.
Bahkan diagram skematik ini cukup untuk memahami bahwa kita berhadapan dengan sejumlah besar kandidat potensial untuk menyelesaikan sistem. Mengapa kandidat? Karena beberapa titik integer dari hiperbola akan menjadi kuadrat penuh, mis. solusi yang tidak pantas. Dan jika Anda membayangkan bahwa ada ketentuan tambahan yang dikenakan pada setiap variabel dalam sistem, maka menemukan kandidat untuk solusi akan menjadi sangat sulit. Dan sejauh ini kita hanya berbicara tentang sistem tiga persamaan.
Tapi mari kita kembali ke "formula" bilangan prima kita. Apa yang ada di depan kita?
Cepat atau lambat, kita akan menemukan bahwa parameter
n dalam persamaan Pell akan menjadi sangat besar. Metode pecahan lanjutan akan menjadi tidak berguna. Kami pasti akan mencoba sesuatu yang lain, misalnya menghitung nilai dengan menyaring, entah bagaimana menggeneralisasi seluruh proses dan datang ke algoritma seperti saringan kuadratik atau saringan bidang angka. Pada akhirnya, kita akan fokus pada metode "chakraval", meskipun itu juga akan mengalami beberapa kesulitan.
Pada saat tertentu, kita akan merasakan kepercayaan pada solusi dari masing-masing persamaan sistem. Tetapi tidak seluruh sistem. Kami akan mencoba menerapkan beberapa metode optimasi heuristik, misalnya, algoritma anil, atau algoritma semut. Tapi di sini kita akan gagal. Untuk setidaknya memahami bagaimana kegagalan ini terjadi, kita harus menyelami sedikit ke dalam geometri aljabar dan topologi. Secara bertahap, kita akan mendapatkan beberapa gagasan tentang "substansi yang dapat dikristalisasi". Kita dapat membayangkan dari jauh struktur wajah yang kita lepaskan semut.
Berdasarkan ide-ide ini, kami akan mencoba meningkatkan algoritme kami. Untuk melakukan ini, kami akan mengambil prestasi terbaik dari banyak cabang matematika. Berangsur-angsur, ada sedikit peluang dalam algoritme, tetapi Anda masih tidak bisa menyingkirkannya. Apa yang akan terjadi selanjutnya? Kami tiba-tiba menemukan bahwa banyak kandidat yang cocok untuk keputusan yang benar di beberapa tempat secara paradoks padat. Setiap kepadatan seperti itu akan memberi harapan bahwa di suatu tempat di pusatnya jawaban tersembunyi itu tersembunyi. Kepadatan seperti itu akan "tampak" bagi semut sebagai sesuatu seperti saluran saluran masuk terbalik. Kami akan mencoba untuk "memukul" pusat dan tertinggi mereka. Tapi apa yang akan terjadi?
Apa yang ada di balik dinding?
Saya mungkin tidak tahu caranya, tetapi kami akan menyelesaikan persamaan ini. Mungkin komputer kuantum atau (!) Quark akan membantu kita. Tapi ini tidak akan menjadi lubang di dinding. Mungkin, bilangan prima Gaussian dan persamaan yang bahkan lebih rumit yang akan mewakili banyak dari mereka akan menunggu kita lebih jauh. Kemudian, mungkin, di antara angka-angka hypercomplex lainnya, kita akan menemukan beberapa jenis perilaku "sederhana". Mungkin ini, pada akhirnya, akan menjadi batas, semacam horizon peristiwa untuk black hole matematika.
Apa yang mungkin ada di bawah cakrawala ini? Mungkin semacam singularitas matematika. Mungkin, kita akan tahu segalanya tentang semua set, kita akan bisa menyelesaikan persamaan dan masalah apa pun. Atau mungkin tidak akan ada lagi pertanyaan dan tugas baru?
Justru pemikiran seperti itulah yang muncul. Sebenarnya, ajukan pertanyaan tentang bilangan prima dan terima kasih untuk persamaan ini Anda bisa mendapatkan jawabannya. Apakah jumlah bilangan prima kembar tak terbatas? Pecahkan persamaan ini, buat beberapa perhitungan aljabar dan dapatkan jawabannya. Apa bilangan prima yang diakhiri dengan 1, 3, 7, atau 9? Algoritma yang sama: beberapa perhitungan dan penggantian persamaan. Apakah Anda ingin cepat menguraikan angka menjadi faktor utama? ..
Kesimpulannya
Saya pertama kali bertemu persamaan ini pada 2008, saat itu saya sudah tergila-gila pada kriptografi dan teori bilangan, khususnya, skema RSA dan masalah faktorisasi. Tentu saja, polinomial yang menghasilkan bilangan prima menurut saya merupakan topik yang sangat menarik, tetapi terlalu rumit. Namun, semua masalah yang bisa atau tidak bisa diselesaikan entah bagaimana terhubung dengan persamaan Diophantine. Oleh karena itu, sudah pada tahun 2014, saya kembali beralih ke polinomial ini, memutuskan untuk hanya menjelajahi semua bagian matematika secara berturut-turut dan mencari sesuatu yang dapat berguna dalam menyelesaikannya. Tentu saja, tidak ada pembicaraan tentang budaya akademis dari semua karya saya - saya tidak pernah menyimpan catatan sistematis, tidak pernah mengumpulkan kode yang dihasilkan. Ini hanya hobi saya.
Pikiran menulis artikel ini muncul setelah saya melihat film Interstellar. Saya tidak bisa percaya bahwa lubang hitam dan gravitasi dapat diwakili dengan sangat menarik. Tapi, ternyata, dunia matematika yang "tidak ada" memberi saya kesan yang sama sepanjang waktu. Dunia ini juga memiliki "ruang dalam" yang tidak dapat diakses dan "partikel elementer" sendiri.
Dengan artikel ini saya ingin menunjukkan bahwa mungkin untuk mendekati setidaknya sedikit untuk tugas apa pun, paling sulit, bahkan tidak mungkin. Ada banyak tugas seperti itu, dan Anda dapat memilih salah satu yang Anda sukai dan paling dekat dengan bidang yang diminati. Tentu saja, kompleksitas yang berlebihan dan kekalahan dijamin akan menghilangkan keinginan sedikit pun dalam usaha ini. Tetapi seluruh paradoksnya adalah bahwa perjalanan dan petualangan yang paling menarik, bahkan di dunia matematika yang "tidak ada", paling sering, dimulai dengan cara ini.