Sebuah studi baru-baru ini,
"Menggunakan dan menghubungkan potongan kode Stack Overflow dalam proyek GitHub," tiba-tiba menemukan bahwa sebagian besar waktu dalam proyek sumber terbuka,
jawaban saya ditulis hampir sepuluh tahun yang lalu. Ironisnya, ada bug.
Sekali waktu ...
Kembali pada tahun 2010, saya duduk di kantor saya dan melakukan omong kosong: Saya
menyukai golf kode dan
menambahkan peringkat ke Stack Overflow.
Pertanyaan berikut ini menarik perhatian saya: bagaimana cara menampilkan jumlah byte dalam format yang dapat dibaca? Artinya, bagaimana mengkonversi sesuatu seperti 123456789 byte menjadi "123,5 MB".
 Antarmuka 2010 yang bagus, terima kasih The Wayback Machine
Antarmuka 2010 yang bagus, terima kasih The Wayback MachineSecara implisit, hasilnya adalah angka antara 1 dan 999.9 dengan unit yang sesuai.
Sudah ada satu jawaban dengan satu lingkaran. Idenya sederhana: periksa semua derajat dari unit terbesar (EB = 10
18 byte) ke terkecil (B = 1 byte) dan terapkan yang pertama, yang kurang dari jumlah byte. Dalam kode pseudo, tampilannya seperti ini:
suffixes = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ] magnitudes = [ 10^18, 10^15, 10^12, 10^9, 10^6, 10^3, 10^0 ] i = 0 while (i < magnitudes.length && magnitudes[i] > byteCount) i++ printf("%.1f %s", byteCount / magnitudes[i], suffixes[i])
Biasanya, dengan jawaban yang benar dengan peringkat positif, sulit untuk mengejarnya. Di Stack Overflow, ini disebut
masalah penembak tercepat di Barat . Tetapi di sini jawabannya memiliki beberapa kekurangan, jadi saya masih berharap untuk mengatasinya. Setidaknya kode dengan loop dapat sangat dikurangi.
Nah ini aljabar, semuanya sederhana!
Kemudian saya sadar. Awalannya adalah kilo-, mega-, giga-, ... - tidak lebih dari derajat 1000 (atau 1024 dalam standar IEC), sehingga awalan yang benar dapat ditentukan menggunakan logaritma, dan bukan siklusnya.
Berdasarkan ide ini, saya menerbitkan yang berikut:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
Tentu saja, ini tidak terlalu mudah dibaca, dan log / pow lebih rendah efisiensinya daripada opsi lain. Tapi tidak ada loop dan hampir tidak ada percabangan, jadi hasilnya cukup indah, menurut saya.
Matematika itu sederhana . Jumlah byte dinyatakan sebagai byteCount = 1000 s , di mana s mewakili derajat (dalam notasi biner, basisnya adalah 1024.) Solusi s memberikan s = log 1000 (byteCount).
Tidak ada log ekspresi sederhana 1000 di API, tetapi kami dapat mengungkapkannya dalam bentuk logaritma natural sebagai berikut s = log (byteCount) / log (1000). Lalu kami mengonversi s ke int, jadi jika, misalnya, kami memiliki lebih dari satu megabita (tetapi tidak satu gigabita penuh), maka MB akan digunakan sebagai unit pengukuran.
Ternyata jika s = 1, maka dimensinya adalah kilobyte, jika s = 2 - megabita dan seterusnya. Bagilah byteCount dengan 1000 s dan tampar huruf yang sesuai ke dalam awalan.
Yang tersisa hanyalah menunggu dan melihat bagaimana masyarakat memahami jawabannya. Saya tidak dapat berpikir bahwa potongan kode ini akan menjadi yang paling banyak beredar dalam sejarah Stack Overflow.
Studi Atribusi
Maju cepat ke 2018. Mahasiswa pascasarjana Sebastian Baltes menerbitkan sebuah artikel di jurnal ilmiah
Empirical Software Engineering berjudul
"Menggunakan dan Mengaitkan Potongan Kode Stack Overflow dalam Proyek GitHub" . Topik penelitiannya adalah seberapa besar lisensi Stack Overflow CC BY-SA 3.0 dihormati, yaitu, yang penulis tunjukkan ke tautan Stack Overflow sebagai sumber kode.
Untuk analisis, potongan kode diekstraksi dari
dump Stack Overflow dan dipetakan ke kode di repositori GitHub publik. Kutipan dari abstrak:
Kami menyajikan hasil studi empiris skala besar yang menganalisis penggunaan dan atribusi fragmen non-sepele kode Java dari jawaban SO dalam proyek GitHub (GH) publik.
(Spoiler: tidak, sebagian besar programmer tidak mematuhi persyaratan lisensi).
Artikel memiliki tabel seperti itu:
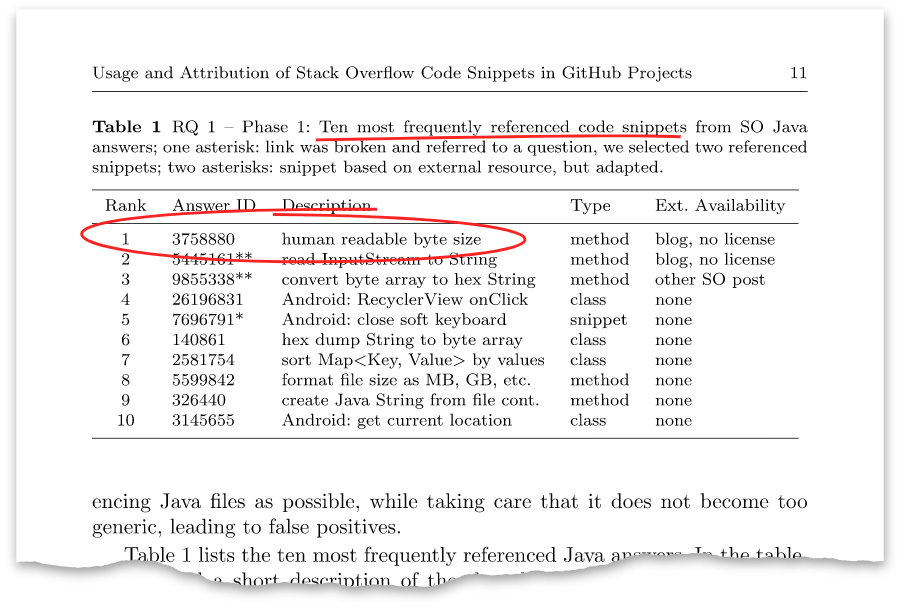
Jawaban di atas dengan pengidentifikasi
3758880 ternyata menjadi jawaban yang saya posting delapan tahun lalu. Saat ini, ia memiliki lebih dari seratus ribu pandangan dan lebih dari seribu plus.
Pencarian cepat di GitHub benar-benar menghasilkan ribuan repositori dengan kode
humanReadableByteCount .
Cari fragmen ini di repositori Anda:
$ git grep humanReadableByteCount
Sebuah cerita lucu , ketika saya mengetahui tentang penelitian ini.
Sebastian menemukan kecocokan dalam repositori OpenJDK tanpa atribusi apa pun, dan lisensi OpenJDK tidak kompatibel dengan CC BY-SA 3.0. Pada milis jdk9-dev, ia bertanya: apakah kode Stack Overflow disalin dari OpenJDK atau sebaliknya?
Yang lucu adalah saya hanya bekerja di Oracle, dalam proyek OpenJDK, jadi mantan kolega dan teman saya menulis yang berikut ini:
Hai
Mengapa tidak bertanya kepada penulis postingan ini langsung di SO (aioobe)? Dia adalah anggota OpenJDK dan bekerja di Oracle ketika kode ini muncul di repositori sumber OpenJDK.
Oracle menangani masalah ini dengan sangat serius. Saya tahu bahwa beberapa manajer merasa lega ketika mereka membaca jawaban ini dan menemukan "pelakunya".
Lalu Sebastian menulis kepada saya untuk mengklarifikasi situasi, yang saya lakukan: kode ini ditambahkan sebelum saya bergabung dengan Oracle dan saya tidak ada hubungannya dengan komit. Lebih baik tidak bercanda dengan Oracle. Beberapa hari setelah tiket dibuka, kode ini dihapus .
Bug
Saya yakin Anda sudah memikirkan hal itu. Apa jenis kesalahan dalam kode?
Sekali lagi:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
Apa saja pilihannya?
Setelah exabytes (10
18 ) adalah zettabytes (10
21 ). Mungkin jumlah yang sangat besar akan melampaui kMGTPE? Tidak. Nilai maksimum adalah 2
63 -1 ≈ 9,2 × 10
18 , jadi tidak ada nilai yang akan melampaui exabytes.
Mungkin kebingungan antara unit SI dan sistem biner? Tidak. Ada kebingungan dalam versi pertama jawaban, tetapi itu diperbaiki cukup cepat.
Mungkin exp berakhir dengan zeroing, menyebabkan charAt (exp-1) macet? Tidak juga. Pernyataan if pertama mencakup kasus ini. Nilai exp akan selalu minimal 1.
Mungkin beberapa kesalahan pembulatan yang aneh dalam ekstradisi? Yah, akhirnya ...
Banyak sembilan
Solusinya bekerja sampai mendekati 1 MB. Ketika
"1000,0 kB" byte ditentukan sebagai input, hasilnya (dalam mode SI) adalah
"1000,0 kB" . Meskipun 999.999 lebih dekat ke 1000 × 1000
1 daripada ke 999.9 × 1000
1 , 1000 penanda dilarang oleh spesifikasi. Hasil yang benar adalah
"1.0 MB" .
Dalam pembelaan saya, saya dapat mengatakan bahwa pada saat penulisan, kesalahan semacam itu ada di semua 22 jawaban yang dipublikasikan, termasuk Apache Commons dan perpustakaan Android.
Bagaimana cara memperbaikinya? Pertama-tama, kami mencatat bahwa eksponen (exp) harus berubah dari 'k' ke 'M' segera setelah jumlah byte lebih dekat ke 1 × 1.000
2 (1 MB) daripada ke 999.9 × 1000
1 (999.9 k ) Ini terjadi pada 999.950. Demikian juga, kita harus beralih dari 'M' ke 'G' ketika kita melewati 999.950.000 dan seterusnya.
Kami menghitung ambang ini dan meningkatkan
exp jika
bytes lebih besar:
if (bytes >= Math.pow(unit, exp) * (unit - 0.05)) exp++;
Dengan perubahan ini, kode berfungsi dengan baik hingga jumlah byte mendekati 1 EB.
Lebih banyak Nines
Saat menghitung 999 949 999 999 999 999 999, kodenya memberikan
1000.0 PB , dan hasil yang benar adalah
999.9 PB . Secara matematis, kodenya akurat, jadi apa yang terjadi di sini?
Sekarang kita dihadapkan pada kendala
double .
Pengantar aritmatika floating point
Menurut spesifikasi IEEE 754, nilai floating point mendekati nol memiliki representasi yang sangat padat, sedangkan nilai besar memiliki representasi yang sangat jarang. Bahkan, setengah dari semua nilai adalah antara -1 dan 1, dan ketika datang ke angka besar, nilai ukuran Long.MAX_VALUE tidak berarti apa-apa. Dalam arti harfiah.
double l1 = Double.MAX_VALUE; double l2 = l1 - Long.MAX_VALUE; System.err.println(l1 == l2); // prints true
Lihat "Bit Poin Mengambang" untuk detailnya.
Masalahnya diwakili oleh dua perhitungan:
- Divisi dalam
String.format dan
- Ambang ekspansi
exp
Kita bisa beralih ke
BigDecimal , tapi itu membosankan. Selain itu, masalah juga muncul di sini, karena API standar tidak memiliki logaritma untuk
BigDecimal .
Mengurangi nilai antara
Untuk mengatasi masalah pertama, kita dapat mengurangi nilai
bytes ke rentang yang diinginkan, di mana akurasi lebih baik, dan menyesuaikan
exp . Bagaimanapun, hasil akhir dibulatkan, jadi tidak masalah bahwa kita membuang angka yang paling tidak signifikan.
if (exp > 4) { bytes /= unit; exp--; }
Pengaturan bit paling tidak signifikan
Untuk menyelesaikan masalah kedua
, bit paling
tidak penting penting bagi kami (99994999 ... 9 dan 99995000 ... 0 harus memiliki derajat yang berbeda), jadi kami harus menemukan solusi yang berbeda.
Pertama, perhatikan bahwa ada 12 nilai ambang yang berbeda (6 untuk setiap mode), dan hanya satu yang mengarah ke kesalahan. Hasil yang salah dapat diidentifikasi secara unik karena berakhir pada D00
16 . Jadi Anda bisa memperbaikinya secara langsung.
long th = (long) (Math.pow(unit, exp) * (unit - 0.05)); if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 52 : 0)) exp++;
Karena kami bergantung pada pola bit tertentu dalam hasil floating point, kami menggunakan pengubah ff ketat untuk memastikan bahwa kode bekerja secara independen dari perangkat keras.
Nilai input negatif
Tidak jelas dalam keadaan apa sejumlah byte negatif mungkin masuk akal, tetapi karena Java tidak memiliki
long tidak ditandatangani, yang terbaik adalah menangani opsi ini. Saat ini, input seperti
-10000 B menghasilkan
-10000 BMari kita menulis
absBytes :
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
Ekspresi ini sangat verbose karena
-Long.MIN_VALUE == Long.MIN_VALUE . Sekarang kita melakukan semua perhitungan
exp menggunakan
absBytes bukan
bytes .
Versi final
Ini adalah versi terakhir dari kode, disingkat dan diringkas dalam semangat versi aslinya:
Perhatikan bahwa ini dimulai sebagai upaya untuk menghindari loop dan percabangan yang berlebihan. Tetapi setelah menghaluskan semua situasi perbatasan, kode tersebut menjadi lebih mudah dibaca daripada versi aslinya. Secara pribadi, saya tidak akan menyalin fragmen ini dalam produksi.
Untuk versi terbaru dari kualitas produksi, lihat artikel terpisah:
"Memformat ukuran byte dalam format yang dapat dibaca .
"Temuan Kunci
- Mungkin ada kesalahan dalam jawaban untuk Stack Overflow, bahkan jika mereka memiliki ribuan nilai tambah.
- Periksa semua kasus batas, terutama dalam kode dengan Stack Overflow.
- Aritmatika titik mengambang rumit.
- Pastikan untuk menyertakan atribusi yang benar saat menyalin kode. Seseorang mungkin membawa Anda ke air bersih.