Di hampir setiap permainan kartu setelah permainan, Anda perlu mengocok kartu. Sementara saya mengocok kartunya, pertanyaan selalu muncul di hadapan saya: "Sudah cukup?" Ini adalah pertanyaan serius - saya tidak ingin menghabiskan terlalu banyak waktu, dan bermain di geladak yang dibebankan juga tidak menyenangkan.

Artikel itu akan membahas situasinya.

Cara Acak

Ada cara-cara keren untuk mengacak kartu, mengacak, misalnya.

Saya tidak tahu caranya, dan kartu kardus tidak dapat dikocok seperti itu, jadi saya mengocoknya dengan cara yang sederhana, tampilannya seperti ini:

Pertama, saya memisahkan bagian dari dek, kemudian saya membuang bagian ini ke sisi lain, dan kemudian saya melaporkan bagian yang tersisa. Menurut pengamatan saya, orang mengocok kartu persis seperti ini atau dekat dengannya. Secara umum, ini dapat dibagi menjadi sejumlah besar bagian, tetapi ini sudah detail. Dalam artikel ini kita akan menganalisis metode acak ini.

Apa itu tata letak kartu acak?

Hal pertama yang terpikir oleh saya adalah tata letaknya yang baik, kartu apa pun bisa berada di posisi ke-i.

Tetapi ini tidak cukup. Misalnya, jika Anda memotong dek - membaginya menjadi dua di tempat acak dan menukar mereka - maka kartu pertama akan sama-sama mungkin ada. Tetapi pada saat yang sama, ini jelas tata letak yang buruk: setelah masing-masing kartu, kecuali beberapa, kartu yang sama akan pergi yang meletakkan setelah itu sebelum "memotong". Artinya, pemain akan menerima kartu "berkorelasi". Dalam kasus orang bodoh, yang satu akan dipukuli, dan yang lain akan dipukuli, dan ini tidak akan disengaja.

Pendekatan lain untuk menentukan tata letak yang baik adalah bahwa di tempat i + 1 ada kartu yang terpisah dari kartu di tempat ke-i. Anda dapat membayangkannya seperti ini: jika Anda melihat kartu paling atas dari kartu, Anda tidak dapat menebak kartu mana yang akan berikutnya.

Pendekatan ini mungkin juga memiliki masalah yang diselesaikan dengan mempertimbangkan distribusi bersama yang besar, tetapi untuk analisis saat ini akan sangat cocok untuk kita.

Bagaimana mengukur "kebaikan" dari tata letak

Kami mengambil deck yang tersisa dari game sebelumnya. Kami menomori semua kartu secara berurutan. Situasi yang buruk adalah ketika setelah mengocok di beberapa tempat setelah kartu dengan nomor i ada kartu dengan nomor i +1. Oleh karena itu, kami akan mengukur proporsi kartu yang berurutan setelah pengocokan.

def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total 

Jelas bahwa meskipun dalam tumpukan yang dikocok dengan baik, beberapa kartu akan jatuh secara berurutan. Bagian mereka akan rata-rata 1 / (n-1), di mana n adalah jumlah kartu di dek.

Hasil

Kami menghitung probabilitas kartu berturut-turut untuk setumpuk 52 kartu, tergantung pada jumlah iterasi pencampuran.

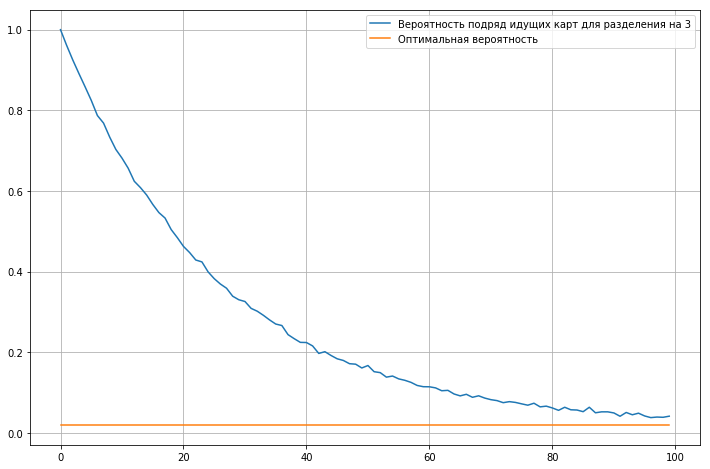
Grafik menunjukkan bahwa bahkan setelah ratusan iterasi, probabilitas kartu berurutan adalah sekitar dua kali lebih tinggi dari probabilitas ideal.

 import random def two_split_shuffle(a): s1 = random.randint(1,len(a)-1) s2 = random.randint(1,len(a)-1) s_min = min(s1, s2) s_max = max(s1, s2) p1 = a[:s_min] p2 = a[s_min:s_max] p3 = a[s_max:] return p3 + p2 + p1 def shuffle_n(a, f, n): for _ in range(n): a = f(a) return a def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total def expected(f, n = 100): s = 0 for _ in range(n): s += f() return s / n def get_expected_next_stat(shuf, n, cards): return expected(lambda: next_stat(shuffle_n(range(cards), shuf, n))) cards = 52 x = range(100) y = map(lambda i: get_expected_next_stat(two_split_shuffle, i, cards), x) import matplotlib.pyplot as plt %matplotlib inline plt.figure(figsize=(12,8)) plt.plot(x, y, label = u'       3') plt.plot(x, [1./(cards-1)] * len(x), label = u' ') plt.grid() plt.legend() 

Secara umum, kita dapat mengasumsikan bahwa 60 iterasi adalah jumlah optimal, lebih sedikit pasti buruk. Saya melakukan sekitar 16-17 iterasi dalam 30 detik. Ini berarti bahwa untuk pengocokan normal akan memakan waktu hampir dua menit .

Teman-teman saya dan saya tidak pernah mengocok kartu sebanyak itu. Dan ini berarti bahwa game kami sangat dipengaruhi oleh keseimbangan dari game terakhir.

Hati-hati :)