Metode Newton-Cotes adalah kombinasi teknik integrasi perkiraan berdasarkan:
- pemisahan interval integrasi ke dalam interval yang sama;
- perkiraan integrand pada interval yang dipilih oleh polinomial;
- menemukan luas total trapesium melengkung yang diperoleh.
Artikel ini akan membahas beberapa metode Newton-Cotes:
- metode trapesium;
- Metode Simpson;
- Metode Romberg.
Metode trapesium
Metode trapesium adalah yang paling sederhana dari yang dipertimbangkan. Sebagai contoh, ambil integral berikut:
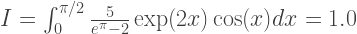
Keakuratan perkiraan tergantung pada jumlah N segmen ke dalam mana interval integrasi dibagi. Dengan demikian, panjang celah:
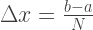
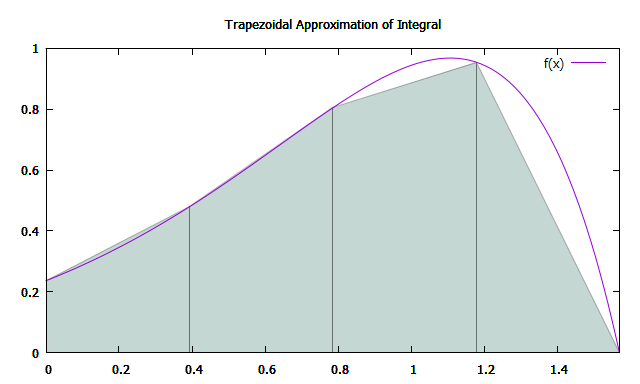
Luas trapesium dapat dihitung dengan rumus:
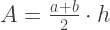
Merangkum semua hal di atas, nilai perkiraan integral dihitung dengan rumus:
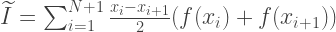
Fungsi yang menghitung integral dengan metode trapesium harus mengambil 4 parameter:
- batas-batas segmen integrasi;
- fungsi integrand;
- angka N interval partisi.
double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double trapezoidal_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2)); } return trapezoidal_integral; }
Metode Simpson
Metode Simpson terdiri dalam mengintegrasikan polinomial interpolasi tingkat kedua dari fungsi f (x) dengan simpul interpolasi a, b, dan m = (a + b) / 2, parabola p (x). Untuk meningkatkan akurasi, masuk akal untuk membagi interval integrasi ke dalam N interval yang sama ( dengan analogi dengan metode trapesium), yang masing-masing menerapkan metode Simpson.
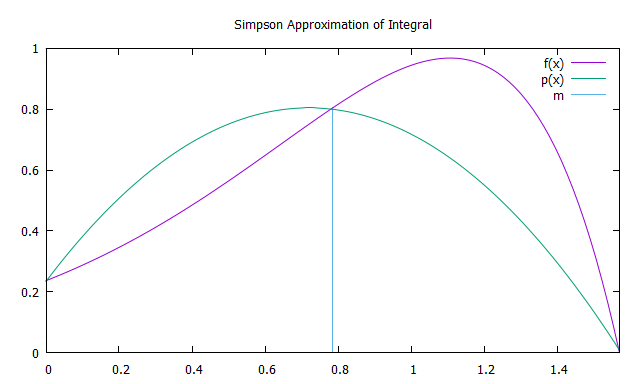
Luas parabola dapat ditemukan dengan menjumlahkan luas 6 persegi panjang dengan lebar yang sama. Ketinggian yang pertama harus sama dengan f (a), dari yang ketiga hingga kelima - f (m), keenam - f (m). Dengan demikian, perkiraan dengan metode Simpson ditemukan oleh rumus:
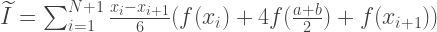
double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double simpson_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2)); } return simpson_integral; }
Metode Romberg
Misalkan T (x) menjadi pendekatan integral yang diperoleh dengan metode trapesium dengan langkah x. Kami mendapatkan 3 perkiraan seperti itu, mengurangi ukuran langkah sebanyak 2 kali dengan setiap perhitungan.

Kami sekarang membangun parabola simetris sehubungan dengan sumbu y, melewati titik T (1) dan T (1/2) untuk mengekstrapolasi nilai yang diperoleh untuk x cenderung ke 0.
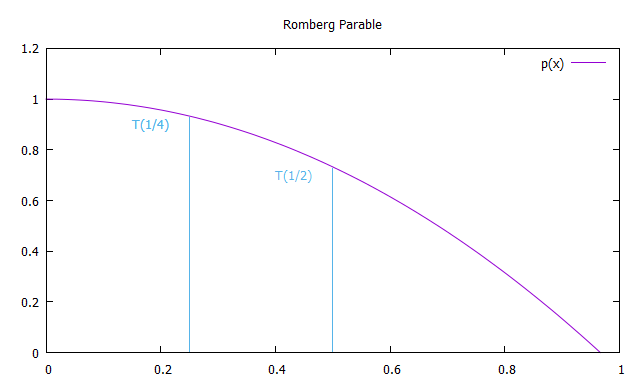
Oleh karena itu, setiap anggota kolom pertama R (n, 0) dari pendekatan Romberg setara dengan solusi yang diperoleh dengan metode trapesium, dan setiap solusi dari kolom kedua R (n, 1) setara dengan metode Simpson. Dengan demikian, rumus untuk perkiraan integrasi dengan metode Romberg:
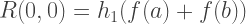
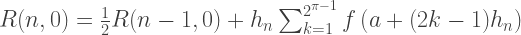
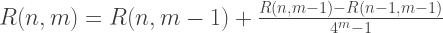
Implementasi C ++:
std::vector<std::vector<double>> rombergIntegral(double a, double b, size_t n, const std::function<double (double)> &f) { std::vector<std::vector<double>> romberg_integral(n, std::vector<double>(n)); romberg_integral.front().front() = trapezoidalIntegral(a, b, 1, f); double h = ba; for(size_t step = 1; step < n; step++) { h *= 0.5; double trapezoidal_integration = 0; size_t stepEnd = pow(2, step - 1); for(size_t tzStep = 1; tzStep <= stepEnd; tzStep++) { const double deltaX = (2*tzStep - 1)*h; trapezoidal_integration += f(a + deltaX); } romberg_integral[step].front() = 0.5*romberg_integral[step - 1].front() + trapezoidal_integration*h; for(size_t rbStep = 1; rbStep <= step; rbStep++) { const double k = pow(4, rbStep); romberg_integral[step][rbStep] = (k*romberg_integral[step][rbStep-1] - romberg_integral[step-1][rbStep-1])/(k-1); } } return romberg_integral; }