Warna Bulan dan Matahari dari ruang angkasa dalam hal RGB dan suhu warna

Tampaknya pertanyaan tentang warna Bulan dan Matahari dari ruang angkasa bagi sains modern begitu sederhana sehingga di abad kita seharusnya tidak ada masalah sama sekali dengan jawabannya. Kita berbicara tentang warna ketika mengamati dengan tepat dari luar angkasa, karena atmosfer menyebabkan perubahan warna karena hamburan cahaya Rayleigh. "Tentunya di suatu tempat di ensiklopedia tentang ini secara rinci, dalam jumlah yang telah lama ditulis," Anda akan mengatakan. Nah, sekarang coba cari di internet untuk informasi tentang itu. Terjadi? Kemungkinan besar tidak. Maksimum yang akan Anda temukan adalah beberapa kata tentang fakta bahwa Bulan memiliki warna kecoklatan, dan Matahari kemerahan. Tetapi Anda tidak akan menemukan informasi tentang apakah warna ini dapat dilihat oleh mata manusia atau tidak, terutama arti warna dalam RGB atau setidaknya suhu warna. Tetapi Anda akan menemukan banyak foto dan video di mana Bulan dari ruang angkasa benar-benar abu-abu, sebagian besar dalam foto-foto program Apollo Amerika, dan di mana Matahari dari ruang angkasa digambarkan putih dan bahkan biru.

Khususnya pendapat pribadi saya hanyalah konsekuensi dari intervensi politik dalam sains. Lagi pula, warna-warna Bulan dan Matahari dari angkasa langsung berhubungan dengan penerbangan orang Amerika ke Bulan.

Saya mencari melalui banyak artikel ilmiah dan buku-buku untuk mencari informasi tentang warna Bulan dan Matahari dari luar angkasa. Untungnya, ternyata meskipun mereka tidak memiliki jawaban langsung ke RGB, ada informasi lengkap tentang kerapatan spektral radiasi matahari dan reflektifitas Bulan melintasi spektrum. Ini cukup untuk mendapatkan warna akurat dalam nilai RGB. Anda hanya perlu menghitung dengan cermat apa yang sebenarnya saya lakukan. Pada artikel ini saya akan membagikan hasil perhitungan dengan Anda dan, tentu saja, saya akan memberi tahu Anda secara rinci tentang perhitungan itu sendiri. Dan Anda akan melihat Bulan dan Matahari dari ruang angkasa dalam warna-warna asli!

Saya melakukan perhitungan dalam program Mathcad dan, dengan demikian, fragmen kode akan berada dalam bahasa pemrograman built-in, yang cukup cocok karena dapat dimengerti untuk semua kode semu.

Pada saat yang sama saya akan memberi tahu Anda secara rinci apa model warna RGB, yang, saya pikir, Anda semua sudah familiar. Pertanyaan ini juga tidak sepenuhnya sederhana. Misalnya, coba jawab dua pertanyaan berikut. Biarkan warna diatur ke rgb (120,80.100) .
1) Nilai RGB apa yang memiliki warna 2 kali lebih gelap dari yang ditentukan?
2) Berapa nilai RGB berwarna abu-abu dengan kecerahan yang sama dengan yang ditentukan?
Tampaknya ada pemikiran, dibagi 2 dalam kasus pertama, yaitu rgb (60.40.50) dan rata-rata dalam kasus kedua, yaitu rgb (100.100.100) . Sayangnya, jawaban yang benar adalah: 1) rgb (86.56.71) ; 2) rgb (92.92.92) . Anda akan mengetahui mengapa jawabannya persis seperti itu.

Juga bicarakan suhu warna dan cara menghitungnya.

Ruang warna XYZ

XYZ adalah model warna utama, yang didefinisikan dalam pengertian matematika yang ketat oleh CIE (International Commission on Illumination) Organisasi Internasional untuk Penerangan pada tahun 1931. Model CIE XYZ adalah model master dari hampir semua model warna lain yang digunakan dalam bidang teknis. Warna XYZ diatur sebagai berikut:

$$

$$X = \ int _ {390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {x}} (\ lambda) \, d \ lambda \\ Y = \ int _ { 390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda \\ Z = \ int _ {390 \, nm} ^ { 830 \, nm} I (\ lambda) \, {\ overline {z}} (\ lambda) \, d \ lambda$$

dimana $$$I (\ lambda)$ - kerapatan spektral dari setiap nilai fotometrik energi (misalnya, fluks radiasi, kecerahan energi, dll., secara absolut atau relatif) pada rentang panjang gelombang dari 390 hingga 830 nm (ini menurut 2006, pada 1931 kisaran berasal dari 380 hingga 780 nm ); $$${\ overline {x}} (\ lambda)$ , $$${\ overline {y}} (\ lambda)$ , $$${\ overline {z}} (\ lambda)$ - fungsi pencocokan warna. Selain itu, yang penting bagi kami, koordinat Y sesuai dengan kecerahan visual sinyal.

Saya mengunduh fungsi pencocokan warna ini dari sini: [ 1 ]. Di sana, fungsi pencocokan warna didefinisikan untuk bidang tampilan 2 derajat dan 10 derajat . Saya memutuskan untuk melakukan perhitungan untuk kedua kasus, membandingkan hasilnya dan memastikan bahwa, seperti yang diharapkan, koordinat warna sedikit berbeda. Secara alami, saya menggunakan data fungsi dengan resolusi maksimum yang disediakan, yaitu, dengan langkah 0,1 nm . Grafik fungsi pencocokan warna adalah sebagai berikut:



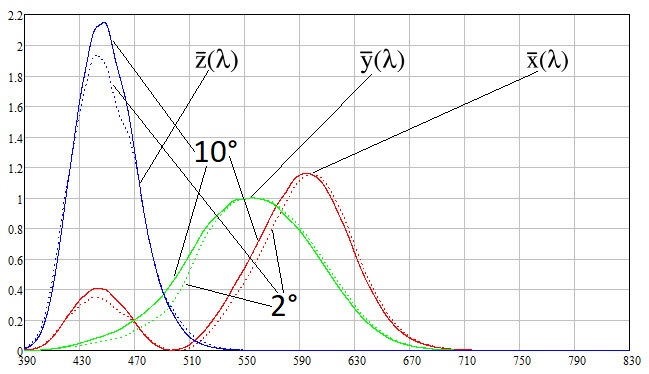
Dari grafik dapat dilihat bahwa di atas 710 nm , fungsi menjadi diabaikan dalam arti bahwa ketika mengamati warna mendekati putih, kerapatan spektral pada kisaran di atas 710 nm membuat hampir tidak ada kontribusi. Meskipun kita tahu bahwa cahaya tampak terletak pada kisaran hingga 780 nm , tetapi kita harus memahami bahwa ini adalah radiasi monokromatik. Saya memiliki semua ini dengan fakta bahwa dalam perhitungan saya harus memperkirakan dalam beberapa kasus data yang hilang pada reflektifitas Bulan hanya untuk rentang di mana fungsi pencocokan warna pada dasarnya kecil. Oleh karena itu, kemungkinan kesalahan ekstrapolasi tidak mengarah ke kesalahan nyata dalam warna yang dihitung.

Saya menghitung integral di atas dengan aturan trapesium :


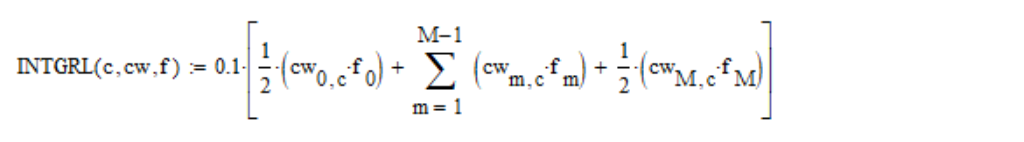
di mana c - adalah bilangan koordinat ruang warna (masing-masing 1, 2, 3 untuk X, Y, Z); cw - adalah tabel fungsi pencocokan warna; f - adalah kerapatan spektral; M = (830-390) /0.1=4400 - jumlah langkah kisi.

Fungsi pencocokan warna yang benar memiliki properti bahwa area di bawah ketiga kurva adalah sama:

$$

$$\ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {x}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {y}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {z}} (\ lambda) \, d \ lambda$$

Ini dilakukan agar spektrum yang seragam memiliki nilai koordinat XYZ yang sama. Periksa apakah properti ini menampung:


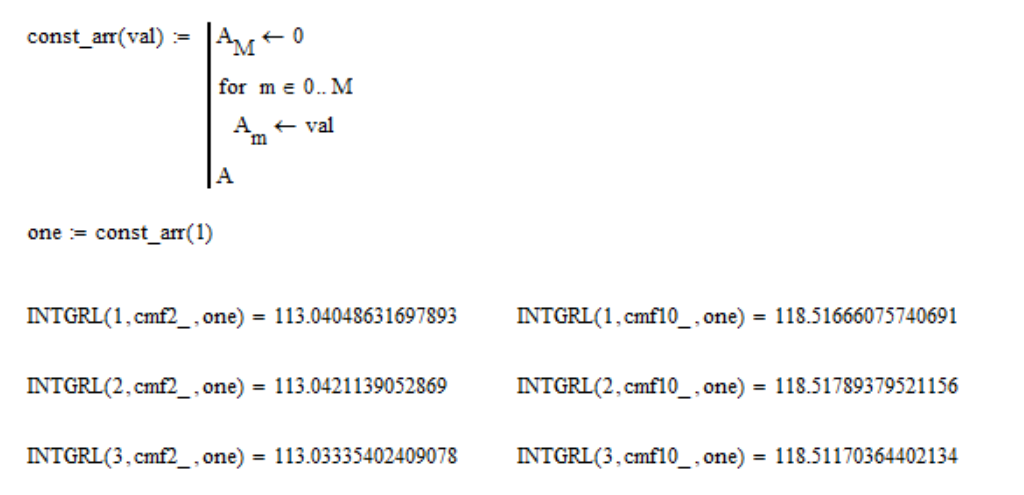
di mana "satu" - adalah array dari 1; cmf2_ dan cmf10_ - masing-masing adalah tabel fungsi pencocokan warna untuk bidang tampilan 2 derajat dan 10 derajat . Seperti yang Anda lihat, properti dilakukan dengan akurasi sekitar 0,01% , yang cukup bagus. Tapi tetap saja, aktifkan kembali fungsi untuk kesetiaan:

Normalisasi kecerahan

Pertimbangkan karya kamera digital. Elemen utama dari kamera digital adalah matriks, yang terdiri dari fotosensor. Ketika gambar diproyeksikan ke matriks, muatan listrik diakumulasikan di masing-masing fotosensornya, yang sebanding dengan energi radiasi fotosensor. Fotosensor menangkap kecerahan elemen gambar, tanpa membawa informasi apa pun tentang warnanya. Untuk informasi tentang warna, matriks sensor fotosensor ditutup oleh filter miniatur. Filter ini menjalankan peran fungsi pencocokan warna. Setiap piksel terdiri dari beberapa sensor foto, yang digabungkan dalam jumlah berbagai filter cahaya.

Jadi, sebagai fungsi $$$I (\ lambda)$ kita harus mengambil kerapatan spektral energi radiasi satu piksel. Kepadatan spektral seperti itu dapat direpresentasikan sebagai

$$

$$I (\ lambda) = coef \ cdot ilumination (\ lambda) \ cdot albedo (\ lambda)$$

di mana iluminasi - adalah kerapatan spektral sumber cahaya; Albedo - reflektifitas permukaan objek yang difoto; coef - adalah koefisien konstan tertentu, yang ditentukan oleh waktu bukaan, bukaan, jarak dari sumber cahaya ke objek yang sedang difoto dan faktor lainnya. Reflektansi mengacu pada albedo yang terlihat , yang didefinisikan sebagai rasio kecerahan elemen permukaan datar yang diterangi oleh sinar paralel terhadap kecerahan permukaan yang benar-benar putih yang terletak tegak lurus terhadap sinar.

Sekarang bayangkan bahwa kita sedang melakukan pekerjaan photoexposure meter, dengan mana fotografer mengatur kecepatan rana dan apertur pada kamera. Dengan kata lain, kita perlu memilih nilai koefisien agar gambar normal dalam kecerahan, tidak terlalu gelap, tidak terlalu cerah. Bayangkan ada layar putih di belakang objek yang sedang difoto. Albedo reflektifitas layar seperti itu menurut definisi sama dengan 1 pada semua panjang gelombang. Tetapkan nilai koefisien sehingga kecerahan visual Y pada layar ini sama dengan 1. Mengapa 1? Karena dalam model warna RGB, nilai kecerahan maksimum yang dimungkinkan adalah 1, yang dicapai dengan rgb (255.255.255) , yaitu, dengan putih. Saya akan menceritakannya nanti. Karena tubuh normal lebih gelap warnanya daripada layar benar-benar putih, gambar akan normal dalam kecerahan. Dari pertimbangan ini, kita mendapatkan ungkapan berikut untuk coef :

$$

$$coef = \ frac {1} {\ int _ {390 \, nm} ^ {830 \, nm} iluminasi (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda}$$

Perlu dicatat bahwa normalisasi semacam itu tidak menjamin bahwa nilai setiap koordinat RGB akan kurang dari atau sama dengan 255. Misalnya, jika Anda memotret layar yang benar-benar putih dengan sumber cahaya merah, maka warna RGB akan padam. skalanya.

Jadi, saya menghitung nilai koordinat ruang warna XYZ sebagai berikut:


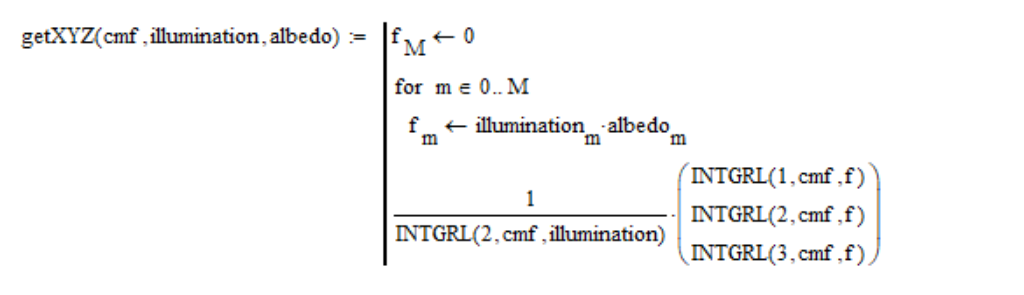
Kita perlu entah bagaimana mengekspresikan warna Matahari. Kami tidak dapat memotretnya secara langsung, dan dalam model matematika kami, kami belum meramalkan kasus ekstrim seperti itu. Jelas, kita perlu memotret permukaan yang benar-benar putih yang diterangi oleh Matahari. Karena Matahari dari luar angkasa memiliki warna kemerahan, maka, seperti yang saya katakan, warna layar yang benar-benar putih tidak sesuai dengan skala. Karena itu, kita harus mengambil permukaan yang lebih gelap. Secara empiris saya menemukan bahwa kita harus mengambil kertas putih dengan albedo 0,91. Albedo lebih banyak tidak dapat diambil, mulai keluar dari skala. Jadi untuk mendapatkan warna Matahari, saya cukup mengatur nilai albedo menjadi 0,91 pada semua panjang gelombang dalam rumus di atas:

ruang warna sRGB

Ruang warna yang paling umum menggunakan model RGB adalah sRGB. Oleh karena itu, ketika mereka berbicara tentang RGB tanpa klarifikasi, itu adalah ruang warna sRGB yang merupakan standar untuk mewakili spektrum warna menggunakan model RGB. Standar ini dibuat oleh Konsorsium Warna Internasional (ICC) pada tahun 1996 untuk menyatukan penggunaan model RGB di monitor, printer dan situs Internet. Mari kita menganalisis standar ini, deskripsi yang tersedia di [ 2 ].

Konversi XYZ ke sRGB berlangsung dalam tiga tahap. Pertama, koordinat XYZ dikonversi menjadi koordinat RGB linier, kemudian koordinat linier dikonversi ke koordinat RGB non-linier, dan pada akhirnya koordinat non-linear dikonversi ke koordinat RGB 8-bit, yang, pada kenyataannya, adalah koordinat dari ruang warna sRGB.

Konversi koordinat XYZ ke koordinat RGB linear adalah sebagai berikut:



dan yang sebaliknya adalah:



Saya bertanya-tanya dari mana angka-angka aneh ini berasal dari matriks persegi? Dan mereka datang dari rekomendasi ITU-R BT.709 [ 3 ]. Nyatakan matriks kuadrat pertama oleh XYZ_to_RGB , dan yang kedua oleh RGB_to_XYZ . Jelas, mereka saling terbalik. Rekomendasi ITU-R BT.709 menetapkan persyaratan untuk matriks kedua. Dari persyaratan ini, Anda dapat secara unik menghitung matriks kedua, dan yang pertama sama dengan matriks terbalik dari yang kedua.

Kami memperkenalkan fungsi-fungsi berikut:

$$

$$XYZ (R, G, B) = RGB \ _to \ _XYZ \ cdot {\ begin {bmatrix} R \\ G \\ B \ end {bmatrix}} \\ W (R, G, B) = XYZ_1 (R , G, B) + XYZ_2 (R, G, B) + XYZ_3 (R, G, B) \\ xy (R, G, B) = \ frac {1} {W (R, G, B)} \ cdot {\ begin {bmatrix} XYZ_1 (R, G, B) \\ XYZ_2 (R, G, B) \ end {bmatrix}}$$

Kemudian persyaratan rekomendasi ITU-R BT.709 mengambil bentuk berikut:

$$

$$xy (1,0,0) = {\ begin {bmatrix} 0.64 \\ 0.33 \ end {bmatrix}}, \; xy (0,1,0) = {\ begin {bmatrix} 0.30 \\ 0.60 \ end {bmatrix}}, \; xy (0,0,1) = {\ begin {bmatrix} 0,15 \\ 0,06 \ end {bmatrix}} \\ xy (1,1,1) = {\ begin {bmatrix} 0,3127 \\ 0,3290 \ end {bmatrix }}$$

Kami memiliki 8 persamaan, ketika kami memiliki 9 elemen yang tidak diketahui dari matriks RGB_to_XYZ , mis. Satu persamaan lagi tidak ada. Dan persamaan yang hilang diberikan secara implisit, saya harus menebak sendiri sebelumnya. Inti dari persamaan ini adalah untuk warna putih, kecerahan visual Y harus sama dengan 1:

$$

$$XYZ_2 (1,1,1) = 1$$

Saya menemukan solusi tepat dari persamaan ini dalam bilangan rasional:


Jika Anda membulatkan angka dalam hasil saya ke empat tempat desimal setelah titik, Anda mendapatkan angka aneh dalam standar Konsorsium Warna Internasional. Dalam perhitungan saya, saya menggunakan matriks tidak bulat, tetapi yang tepat yang disebutkan di atas (sejauh angka floating-point dengan presisi ganda memungkinkan).

Jadi, koordinat linier RGB berdasarkan tabel fungsi pencocokan warna (cmf), kepadatan radiasi spektral (iluminasi) dan reflektivitas (albedo) saya hitung sebagai berikut:



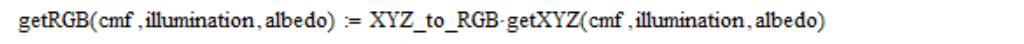
Saya juga menggunakan koordinat linier RGB, rata-rata pada bidang tampilan 2 derajat dan 10 derajat :



Dari koordinat linier RGB, kecerahan visual Y dihitung menggunakan rumus berikut (secara default, array Mathcad diberi nomor mulai dari elemen nol):


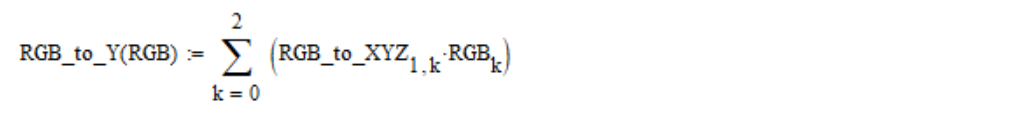
Kami terus membongkar standar. Setiap koordinat linier RGB dikonversi menjadi nonlinear menggunakan fungsi nonlinear lin2bit, dan kembali ke bit2lin, yang didefinisikan sebagai berikut:


Grafik fungsi-fungsi ini terlihat seperti ini:



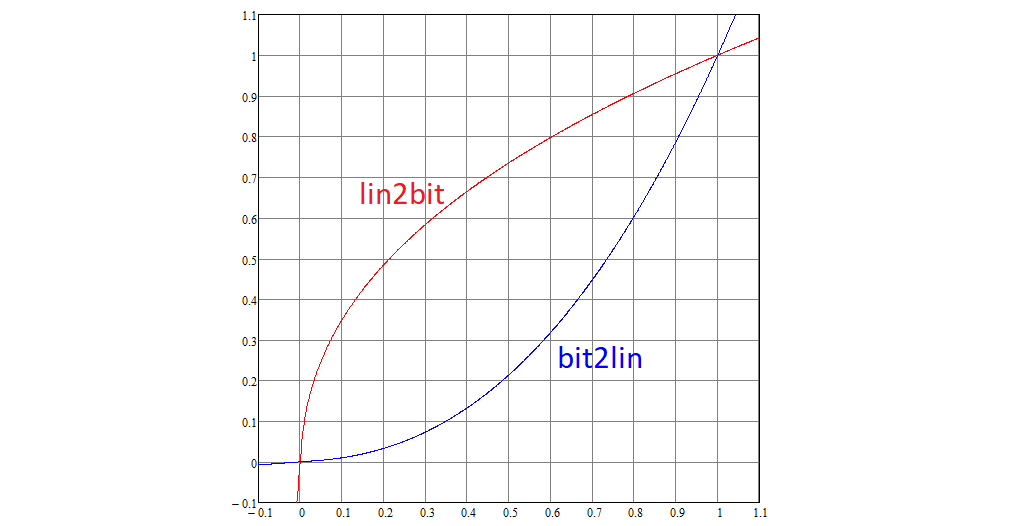
Perhatikan bahwa 0 dikonversi ke 0, 1 ke 1.

Pada akhirnya, koordinat non-linear RGB dikonversi menjadi 8-bit dengan mengalikannya dengan 255, diikuti dengan pembulatan ke angka integer.

Jadi, saya mendefinisikan fungsi-fungsi berikut untuk mengubah koordinat RGB linier menjadi 8-bit dan kembali:

Sekarang kita siap untuk menyelesaikan masalah dari pendahuluan. Saya ingatkan kondisinya.

Biarkan warna diatur ke rgb (120,80.100) .
1) Apa nilai-nilai RGB memiliki warna yang 2 kali lebih gelap dari yang ditentukan?
2) Berapa nilai RGB untuk abu-abu dengan kecerahan yang sama dengan yang diberikan?

Solusi:

Jawaban: 1) rgb (86.56.71) ; 2) rgb (92.92.92) .

Suhu warna

Suhu warna sumber cahaya, diukur dalam Kelvin, ditentukan oleh suhu benda hitam yang terletak di bagan warna di tempat yang sama dengan sumber radiasi yang sedang dipertimbangkan. Jika sumber cahaya tidak jatuh pada kurva Planck (kurva yang ditentukan oleh set titik warna benda hitam pada suhu yang berbeda), suhu warna berkorelasi digunakan untuk menggambarkannya. Nilai ini juga diukur dalam Kelvin ditentukan oleh suhu benda hitam, yang warnanya sedekat mungkin dengan warna sumber cahaya. Untuk menemukan suhu warna berkorelasi dari sumber radiasi pada bagan warna yang dibangun dalam koordinat (u, v) , titik terdekat dengan sumber pada kurva Planck ditentukan (yaitu, jarak geometris terpendek). Suhu benda hitam yang terletak pada titik ini akan sesuai dengan suhu warna berkorelasi dari sumber yang dipertimbangkan [ 4 ].

Untuk benda hitam bersuhu T, daya radiasi per satuan luas permukaan radiasi dalam interval panjang gelombang satuan dinyatakan oleh hukum Planck :

$$

$$R (\ lambda, T) = \ frac {2 \ pi h c ^ 2} {\ lambda ^ 5} \ frac {1} {e ^ {h c / \ lambda k T} -1}$$

Oleh karena itu, saya menghitung kepadatan spektral radiasi benda hitam sebagai berikut (dalam kolom nol dari tabel fungsi pencocokan warna cmf2 adalah nilai panjang gelombang dalam nanometer):



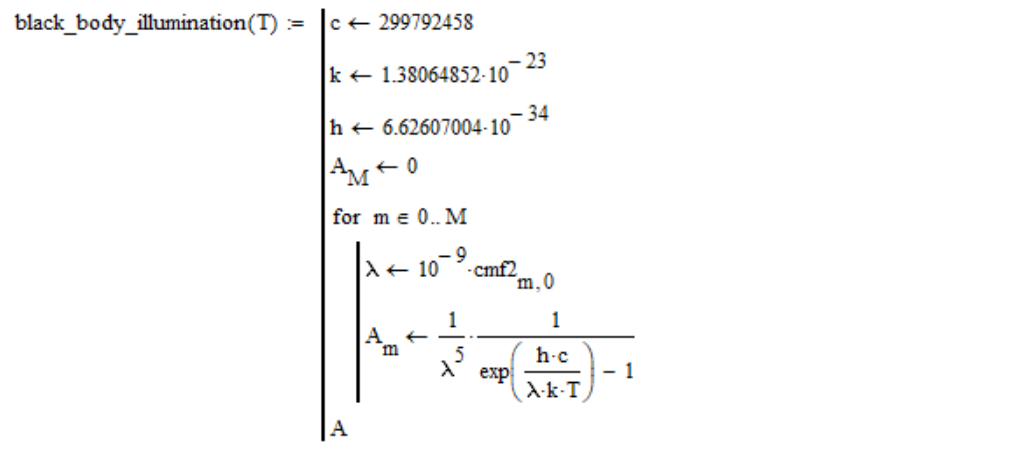
Harap dicatat, saya melewatkan faktor konstan, karena masih dikurangi dengan normalisasi kecerahan lebih lanjut (kecerahan sumber cahaya tidak mempengaruhi suhu warna).

Lalu saya menghitung koordinat linier RGB:



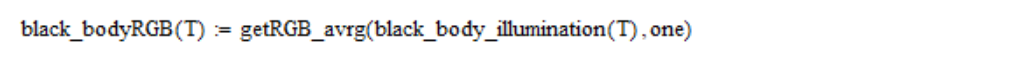
Koordinat linier RGB dikonversi ke (u, v) koordinat sebagai berikut:



Pada bidang (u, v) , jarak geometris antara titik-titik warna yang dipertimbangkan dan warna benda hitam dari suhu tertentu T dihitung:



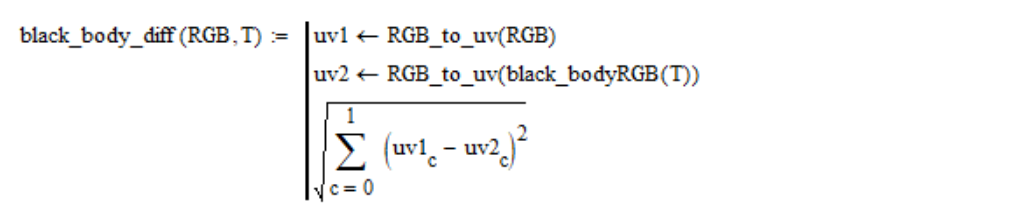
Misalnya, untuk sumber cahaya putih standar, ketergantungan jarak ini pada suhu terlihat seperti ini:



Nilai T di mana ketergantungan ini memiliki minimum adalah suhu warna dari sumber cahaya yang dianggap.

Kepadatan radiasi matahari

Data kepadatan spektral radiasi matahari tanpa atmosfer yang saya unduh dari sini: [ 5 ]. Sumber cahaya yang berhubungan dengan Matahari dari luar angkasa, saya akan sebut sebagai E490 di masa depan. Juga untuk perbandingan dalam perhitungan, saya menganggap D65 standar penerangan . Sumber ini mewakili cahaya putih. Saya melihatnya untuk menunjukkan seperti apa bulan jika matahari putih. Data kepadatan spektral radiasi D65 I illuminant standar yang diunduh dari sini: [ 6 ].

Seperti yang akan ditunjukkan di bawah ini, sumber cahaya D65 dan E490 masing-masing memiliki suhu warna 6467K dan 5912K. Kerapatan radiasi spektral dari sumber cahaya D65, E490 dan benda yang benar-benar hitam pada suhu yang sesuai adalah sebagai berikut:



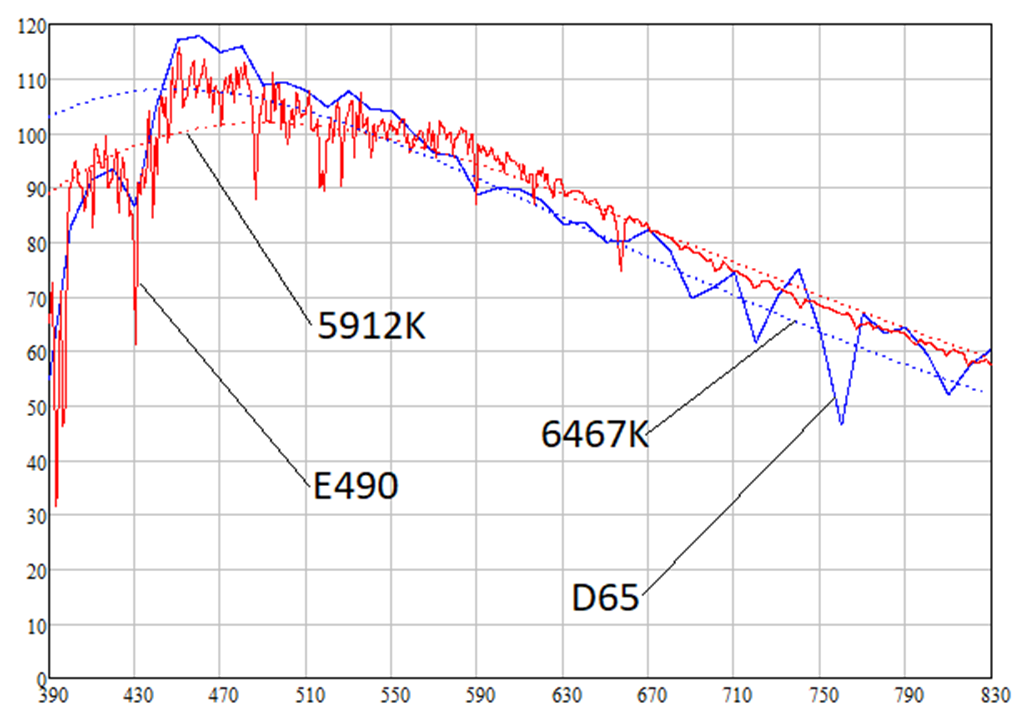
Anda dapat melihat bahwa kerapatan spektrum radiasi matahari lebih tinggi daripada sumber cahaya putih pada panjang gelombang yang lebih panjang, yaitu pada panjang gelombang cahaya merah (620-770 nm). Ini berarti bahwa Matahari memiliki warna kemerahan. Memang, perhitungan memberikan warna berikut dari sumber cahaya D65, E490 dan blackbodies dari suhu yang sesuai (seperti yang saya katakan, kertas putih dengan albedo 0,91 dipertimbangkan):



Perhatikan, koordinat sRGB Matahari dan suhu benda hitam 5912K sama persis. Ini tidak dijelaskan oleh apa pun, itu hanya terjadi.

Warna lingkaran pada gambar terakhir adalah warna sebenarnya dari Matahari dari luar angkasa. Mata manusia dengan jelas melihat warna kemerahan Matahari. Jadi, fakta bahwa Matahari dari ruang angkasa berwarna putih adalah mitos besar! Perlu dicatat bahwa karena alasan tertentu warna ini tidak diamati pada foto dan video Apollo. Dalam foto asli, warna kemerahan Matahari yang terlihat jelas akan muncul di permukaan putih bendera Amerika dan pakaian antariksa. Dan seperti yang akan ditunjukkan di bawah ini, warna Matahari ini memberikan kontribusi yang signifikan terhadap "kemerahan" Bulan dari luar angkasa.

Apakah Bulan berbeda atau warnanya sama?

Penentang teori konspirasi bulan mempromosikan versi bahwa Bulan memiliki warna berbeda. Diduga, Bulan berwarna abu-abu di beberapa tempat, berwarna cokelat di beberapa tempat, dan Apolos mendarat di tempat Bulan berwarna abu-abu. Tetapi versi ini secara langsung bertentangan dengan data ilmiah. Artikel [ 7 ] dengan jelas menyatakan:

Perbedaan warna di Bulan sangat kecil.

Shevchenko juga menulis dalam bukunya [ 8 ]:

Selama bertahun-tahun, peneliti Amerika terkenal T. McCord bekerja ke arah ini. Dia memperoleh lebih dari 200 spektrum untuk berbagai bagian permukaan bulan masing-masing 10-20 km. Semua kurva yang diperoleh pada dasarnya serupa dalam penampilan.

Jadi, tidak, Bulan tidak berbeda warna, tetapi sama.

Data berwarna menurut Shevchenko

Shevchenko dalam bukunya [ 8 ] memberikan ketergantungan reflektifitas berikut pada panjang gelombang.



Dalam perhitungan saya, saya menerapkan interpolasi linear piecewise data ini. Data yang hilang pada interval 820-830 nm, saya terima dengan kelanjutan langsung dari segmen pada interval 690-820 nm.

Warna data menurut LRO

Ketergantungan reflektifitas permukaan bulan pada kondisi iluminasi dan pengamatan pada panjang gelombang dari 321 nm hingga 689 nm diberikan dalam [ 9 ]. Parameter model dihitung berdasarkan analisis data yang diperoleh oleh Lunar Reconnaissance Orbiter (LRO). Kondisi pencahayaan dan pengamatan ditentukan oleh tiga parameter i (sudut datang), e (sudut refleksi) dan g (sudut fase). Sudut-sudut ini ditunjukkan pada diagram berikut:



Sudut fase dapat dinyatakan dalam sudut azimuth $$$\ varPsi$ menggunakan hukum bola cosinus sebagai berikut:

$$

$$g = \ arccos \ kiri (\ cos \ kiri (i \ kanan) \ cos \ kiri (e \ kanan) + \ sin \ kiri (i \ kanan) \ sin \ kiri (e \ kanan) \ cos \ kiri ( \ varPsi \ kanan) \ kanan)$$

Dalam perhitungan, saya mengambil nilai tradisional dari sudut i = g = 30 °, e = 0 °. Untuk sudut seperti itu, ketergantungan berikut reflektifitas pada panjang gelombang diperoleh (grafik lro30):


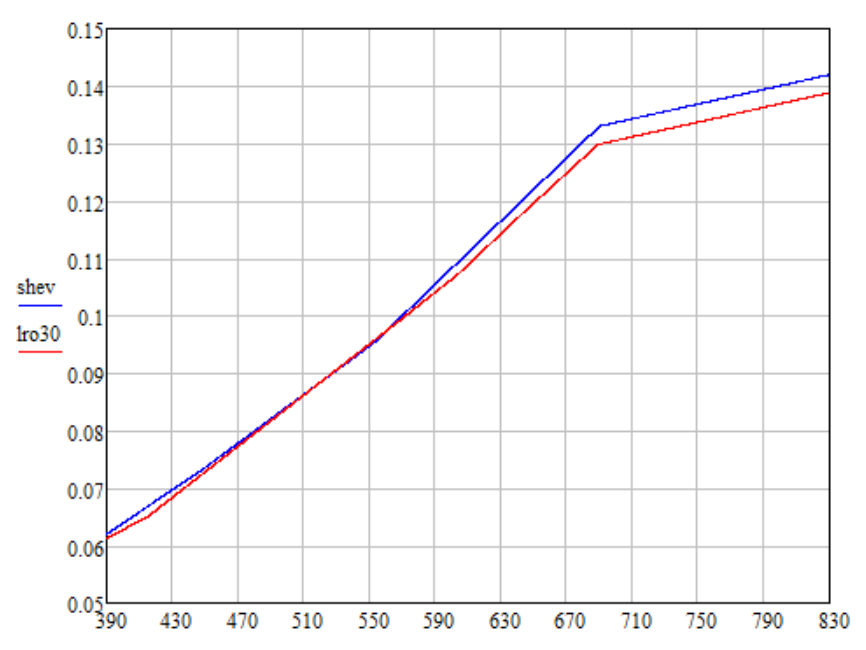
Saya melakukan ekstrapolasi linear data LRO selama interval 689-830 nm sehingga rasio nilai pada titik 830 nm dan 689 nm sama dengan data Shevchenko (plot shev). Saya juga memperbarui nama data Shevchenko dengan mengalikannya dengan 0,8315 sehingga kecerahan warna yang dihasilkan menurut Shevchenko dan LRO adalah sama.

Data berwarna menurut "Kaguya"

Dalam [ 10 ], data yang diperoleh oleh satelit buatan Jepang kedua Bulan disajikan. Sayangnya, reflektivitas dalam rentang panjang gelombang terlihat diberikan dengan resolusi sangat rendah, jadi saya tidak menggunakannya dalam perhitungan saya.

Tetapi karya ini menarik karena berbicara tentang perbedaan kolosal antara data Kaguya dan data misi Apollo 16. Dan ini adalah salah satu kasus yang jarang terjadi ketika komunitas ilmiah secara terbuka berbicara tentang inkonsistensi terkait dengan penerbangan orang Amerika ke Bulan.

Hasil perhitungan

Selanjutnya saya akan menggunakan notasi berikut:
D65 - sumber cahaya putih standar D65;
E490 - sumber cahaya dari Matahari tanpa adanya atmosfer;
W-0.91 - kertas putih dengan Albedo 0.91;
LRO (30 °) - Data LRO untuk sudut tradisional i = g = 30 °, e = 0 °;
Shevch. - data oleh Shevchenko;
lin. (2 °) - koordinat linier RGB dengan bidang pandang 2 derajat ;
lin. (10 °) - koordinat linier RGB dengan bidang pandang 10 derajat ;
lin. (rata-rata) - koordinat linier RGB, rata-rata pada bidang tampilan 2 derajat dan 10 derajat ;
sRGB (100%) - koordinat sRGB, diperoleh dari koordinat linier RGB, rata-rata di atas bidang tampilan 2 derajat dan 10 derajat ;
sRGB (200%) - koordinat sRGB, diperoleh dari koordinat linier berganda RGB, dirata-ratakan pada bidang pandang 2 derajat dan 10 derajat ;
sRGB (300%) - koordinat sRGB, diperoleh dari koordinat linier tiga kali lipat dari RGB, rata-rata pada bidang pandang 2 derajat dan 10 derajat ;
sRGB (400%) - koordinat sRGB, diperoleh dari koordinat linier empat kali lipat dari RGB, rata-rata di atas bidang pandang 2 derajat dan 10 derajat ;
cl. temp. - suhu warna yang diperoleh dari koordinat linier RGB, rata-rata pada bidang tampilan 2 derajat dan 10 derajat ;

D65

	W-0,91	LRO (30 °)	Shevch.
lin. (2 °)	0.9076.0.9120.0.8968	0.1177,0.0931.0.0688	0.1202,0.0931.0.0697
lin. (10 °)	0.9084.0.9122.0.8929	0.1165.0.0916.0.0687	0.1188,0.0917.0.0696
lin. (rata-rata)	0.9080.0.9121.0.8948	0.1171,0.0924.0.0688	0.1195,0.0924.0.0697
sRGB (100%)	rgb (244.245.243)	rgb (96.86.74)	rgb (97.86.75)
sRGB (200%)	-	rgb (133.119.104)	rgb (134.119.104)
sRGB (300%)	-	rgb (160.144.125)	rgb (161.144.126)
sRGB (400%)	-	rgb (182.164.143)	rgb (184.164.144)
cl. temp.	6467K	4928K	4891K

E490

	W-0,91	LRO (30 °)	Shevch.
lin. (2 °)	1.0005.0.8892.0.8490	0.1283.0.0909.0.0649	0.1310.0.0909.0.0657
lin. (10 °)	1,0021,0,8888,0,8483	0.1272.0.0895.0.0650	0.1297.0.0895.0.0659
lin. (rata-rata)	1,0013,0,8890,0,8486	0.1277,0.0902,0.0649	0.1303.0.0902.0.0658
sRGB (100%)	rgb (255.242.237)	rgb (100.85.72)	rgb (101.85.73)
sRGB (200%)	-	rgb (138.118.101)	rgb (140.118.102)
sRGB (300%)	-	rgb (166.142.122)	rgb (168.142.123)
sRGB (400%)	-	rgb (189.162.139)	rgb (191.162.140)
cl. temp.	5912K	4550K	4512K

Gambar berikut menunjukkan warna permukaan Bulan sRGB (100%) , sRGB (200%) (kecerahan dua kali lipat), sRGB (300%) (kecerahan tiga kali lipat), sRGB (400%) (kecerahan empat kali lipat) dengan sumber cahaya E490 (yaitu ketika diamati dari luar angkasa) menurut LRO dan Shevchenko.



Seperti yang Anda lihat, Bulan dari ruang angkasa memiliki warna cokelat, baik menurut data LRO, dan menurut data Shevchenko. Shevchenko ternyata sedikit (hampir tidak terasa) lebih merah dari LRO.

Warna Bulan di foto

Pada bagian ini kita akan melakukan pewarnaan foto. Biarkan img gambar dan warna dalam koordinat linier RGB diberikan. Setiap piksel gambar digantikan oleh piksel warna yang diberikan dengan kecerahan yang sama dengan piksel sumber. Gambar dalam program Mathcad direpresentasikan sebagai matriks koordinat sRGB tunggal, yang diperoleh dengan menjahit tiga matriks "R", "G", "B" dari kiri ke kanan. Dengan mengingat hal ini, prosedur pewarnaan adalah sebagai berikut:

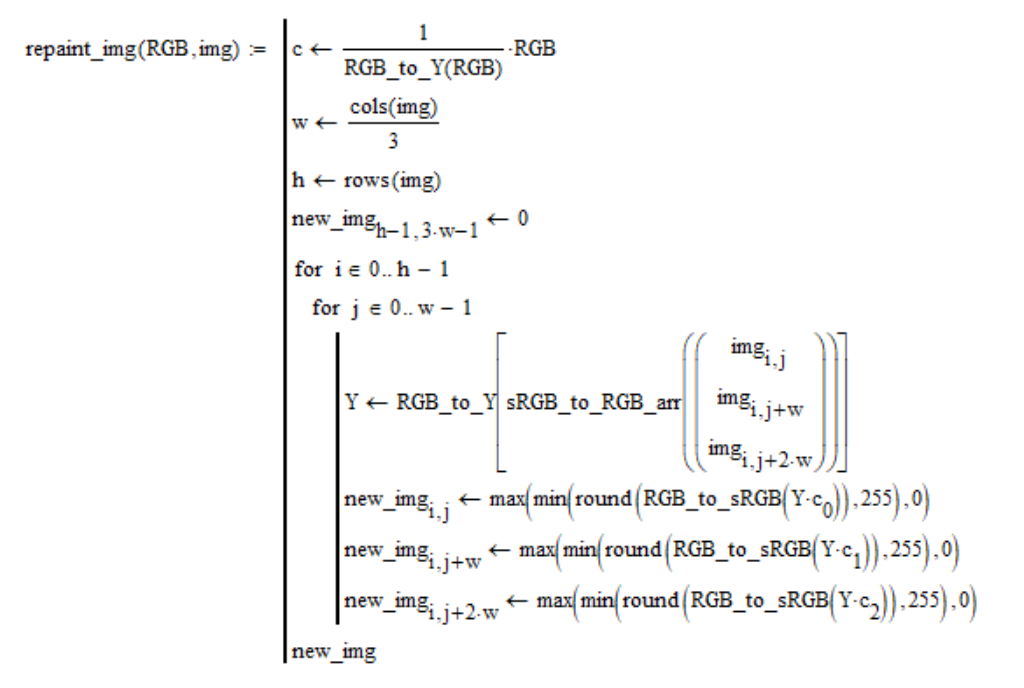
Yang menarik, saya mengambil foto-foto album foto Apollo yang menggambarkan permukaan bulan program Amerika dan mengecatnya dalam warna yang diperoleh dari perhitungan saya. Saya hanya memberikan hasil, dan kesimpulan bahwa ini foto asli atau palsu, buat sendiri.

Hasil gambar AS11-44-6552 mewarnai:



Di tengah adalah foto asli. Di sebelah kiri, foto-foto dicat dalam warna sesuai dengan data LRO pada sudut tradisional i = g = 30 °, e = 0 °, dan di kanan, menurut data Shevchenko. Baris atas sesuai dengan D65 iluminan standar, yaitu baris atas menunjukkan warna permukaan Bulan, yang akan diperoleh jika Matahari berwarna putih. Baris bawah sesuai dengan sumber cahaya E490, yaitu, baris bawah menunjukkan warna alami dari permukaan Bulan seperti yang terlihat dari luar angkasa.

Seperti yang Anda lihat, warna kemerahan Matahari memberi kontribusi signifikan pada "kemerahan" permukaan Bulan, yang pada akhirnya terlihat cokelat, dan bukan abu-abu sama sekali.

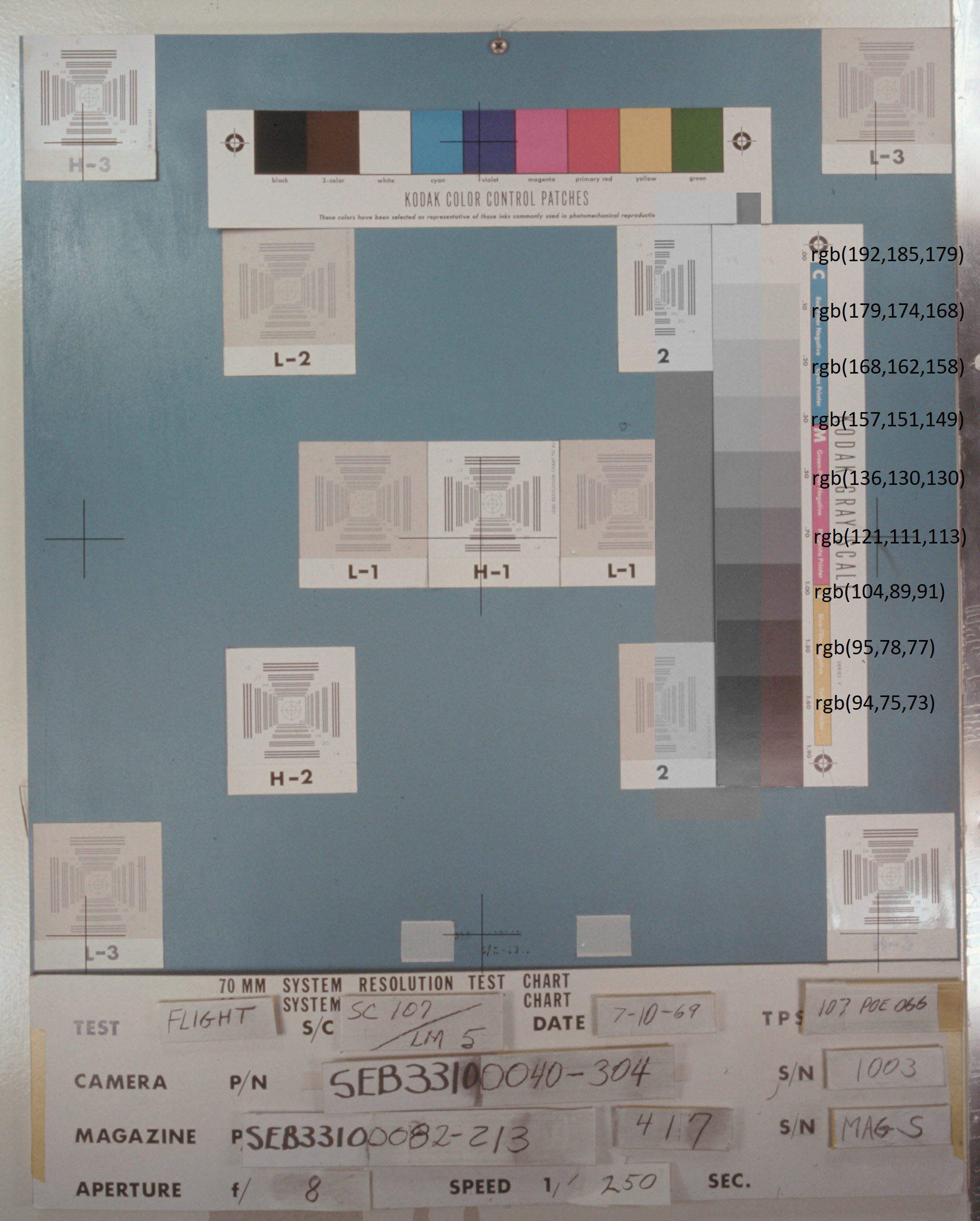
Warna abu-abu Bulan dalam foto-foto NASA dapat dijelaskan oleh fakta bahwa untuk beberapa alasan film "pergi" menjadi biru, tetapi versi ini segera menghilang jika kita menganalisis gambar-gambar gradasi abu-abu di akhir album. Foto as11-44-chart menunjukkan snapshot untuk foto terakhir di atas. Saya menempatkan abu-abu nyata dengan kecerahan yang sama seperti pada foto di sebelah kiri gradasi abu-abu, dan juga menuliskan nilai koordinat sRGB. Hasilnya adalah gambar berikut:



Seperti yang Anda lihat, film ini tidak hanya tidak "pergi" dengan warna biru, tetapi bahkan sedikit "pergi" ke arah yang berlawanan dari biru. Penyimpangan seperti itu tidak bisa berubah menjadi coklat menjadi abu-abu.

Hasil foto mewarnai AS11-40-5903 :



Dalam foto asli, permukaan bulan di tempat-tempat tidak hanya memiliki warna abu-abu, tetapi bahkan sedikit kebiruan. Foto as11-40-grafik menunjukkan gambar gradasi abu-abu yang sesuai:



Film "pergi" bukan ke warna "biru", tetapi ke "merah". Dan bahkan setelah itu, untuk beberapa alasan, permukaan bulan di foto NASA berwarna abu-abu.

Hasil foto mewarnai AS11-37-5455 :



Ini adalah salah satu foto langka dari program "Apollo", di mana permukaan bulan memiliki warna cokelat, meskipun tidak seluruhnya. Penentang teori konspirasi bulan suka menunjukkannya, kata mereka, lihat, cokelat. Tapi triknya sudah merayap di sini. Mari kita menganalisis foto as11-37-chart , yang menunjukkan gambar gradasi abu-abu yang sesuai:



Film ini hanya "meninggalkan" berwarna cokelat. Itulah alasan keseluruhan warna cokelat dari permukaan bulan di foto-foto NASA.

Ketergantungan warna permukaan bulan pada kondisi pencahayaan dan pengamatan

Menggunakan data LRO yang diberikan dalam [ 9 ], kami menyelidiki bagaimana warna permukaan Bulan bervariasi dari kondisi pencahayaan dan pengamatan. Pertimbangkan sumber cahaya E490 (Matahari dari luar angkasa) dan nilai yang berbeda dari sudut i , e , $$$\ varPsi$ . Gambar berikut menunjukkan hasilnya, di mana di baris atas adalah warna dengan kecerahan tiga, dan di baris bawah adalah warna dikurangi menjadi kecerahan yang sama Y = 0,5 .



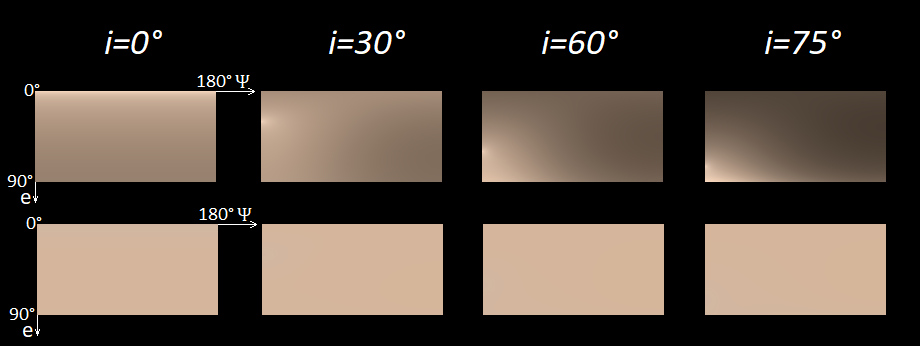
Seperti yang bisa dilihat dari gambar, hanya kecerahan yang berubah. Di baris paling bawah, warnanya hampir sama di mana-mana untuk mata manusia. Meskipun, jika Anda mencermati, dalam kasus i = 0 °, Anda dapat melihat deviasi yang sangat sedikit pada arah abu-abu saat e mendekati nol.

Warna tanah bulan

Situs NASA memiliki foto yang sangat aneh, yaitu foto sampel tanah bulan No. 10005 .



Tanah bulan pada foto terlihat coklat, bahkan terlalu coklat mengingat fakta bahwa pencahayaan dihasilkan oleh sumber cahaya putih. Kebenaran white balance dapat diperiksa oleh warna kertas putih yang masuk ke dalam bingkai.

Mungkin ini adalah tanah oranye yang sama dengan yang ditemukan para astronot Apollo 17? Tidak! Dokumen [ 11 ] dengan jelas menyatakan bahwa sampel diambil oleh para astronot Apollo 11.

Dan sekarang mari kita dengarkan apa yang dikatakan Neil Armstrong (astronot Apollo 11) dalam sebuah wawancara dengan Patrick Moore [ 12 ] yang dia berikan pada tahun 1970.

Ketika Anda melihat bahan dari jarak dekat, seolah-olah di tangan Anda, Anda menemukan itu abu-abu arang sebenarnya, dan kami tidak pernah dapat menemukan hal-hal yang sangat berbeda dari warna itu.

Ternyata, Neil Armstrong, tidak takut dengan kata itu, berbohong.

Sastra

1. Laboratorium Penelitian Warna & Visi - Fungsi CIE XYZ baru yang diubah dari fungsi LMS CIE (2006)
2. International Color Consortium - Ruang Warna Default Standar untuk Internet: sRGB
3. Rekomendasi ITU-RBT.709 - Nilai parameter untuk standar HDTV untuk produksi dan pertukaran program internasional
4. Robertson R. "Perhitungan suhu warna berkorelasi dan suhu distribusi" / .Opt. Soc. Am. 58, 1528 (1968).
5. Referensi Spektrum Ekstraterrestrial Standar ASTM 2000 E-490-00
6. CIE Standard Illuminant D65
7. "Hasil pertama dari penentuan sifat fisikomekanis dari tanah Bulan", M .: 1970. Gosstroy dari USSR, ed. prof. Dr. Techn. Ilmu Pengetahuan VG Bulycheva, hlm. 8. ("Hasil Pertama Menentukan Sifat Fisika-Mekanik Tanah Bulan", Moskow: 1970. Gosstroy dari Uni Soviet, di bawah kepemimpinan Prof. Dr. Sc. VG Bulychev, hal. 8.)
8. Shevchenko VV, Bulan dan Pengamatannya, 1983, hlm. 91-92. (Shevchenko V.V., Moon dan pengamatannya, 1983, hlm. 91-92.)
9. Hapke, B., B. Denevi, H. Sato, S. Braden, dan M. Robinson (2012), Ketergantungan panjang gelombang dari kurva fase bulan seperti yang terlihat oleh Lunar Reconnaissance Orbiter Kamera Wide-Angle, J. Geophys. Res., 117, E00H15
10. Ohtake, M. et al. (2010), Mendapatkan Reflektansi Absolut Permukaan Lunar Menggunakan SELENE (Kaguya) Data Imager Multiband, Space Sci. Pdt., 154, 57-77
11. THE APOLLO 11 DRIVE TABUNG, Diseksi dan deskripsi oleh Judith H. Allton, NASA (1978)
12. BBC Neil Armstrong berbicara dengan Patrick Moore (1970)