Kami membawa persamaan regresi linier ke dalam bentuk matriks

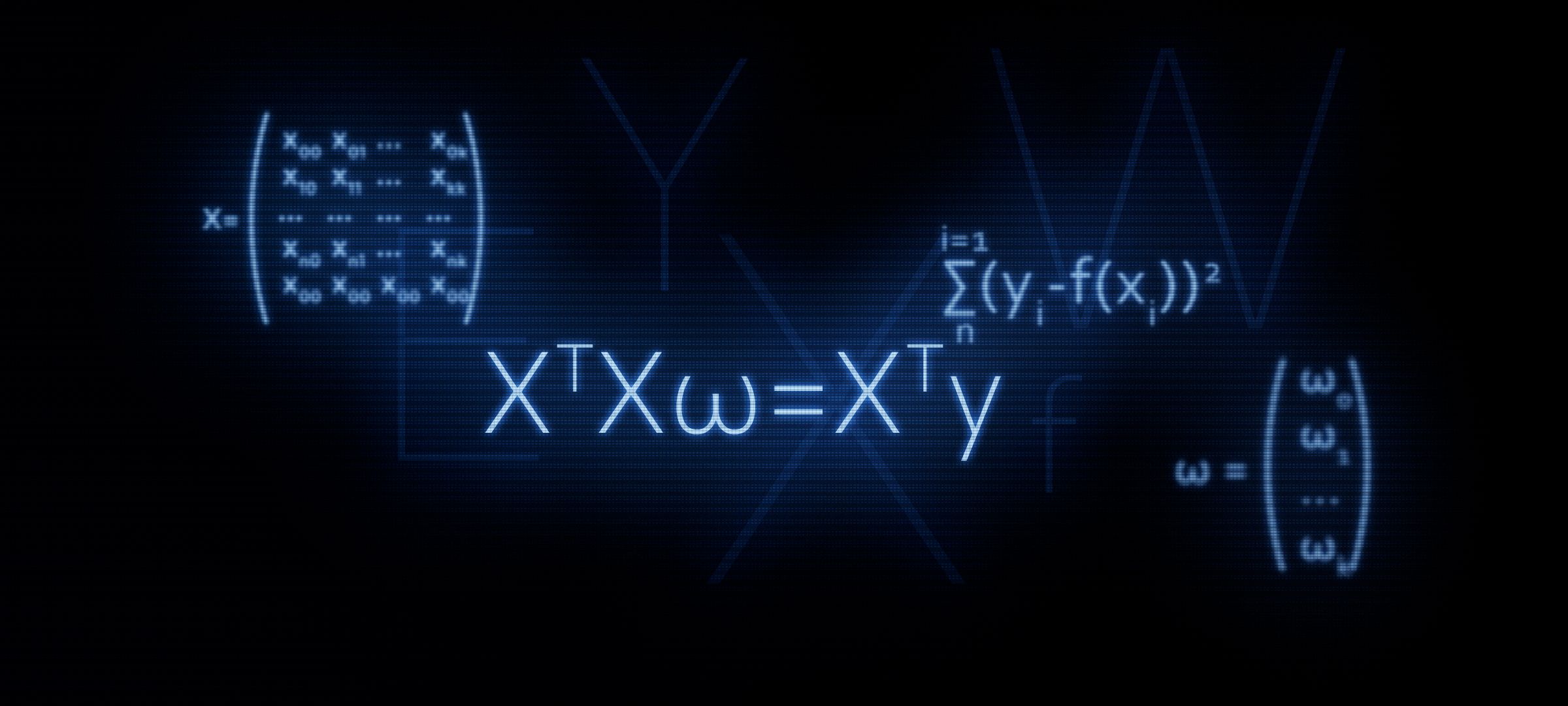
Tujuan artikel ini adalah untuk memberikan dukungan kepada ahli data pemula. Pada artikel sebelumnya, kami menguji tiga metode untuk menyelesaikan persamaan regresi linier: solusi analitis, gradient descent, stochastic gradient descent. Kemudian untuk solusi analitis kami menerapkan formula $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ . Dalam artikel ini, sebagai berikut dari judul, kami akan membenarkan penggunaan formula ini, atau dengan kata lain, kami akan mendapatkannya secara mandiri.

Mengapa masuk akal untuk memberi perhatian lebih pada formula $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ ?

Ini adalah persamaan matriks yang dalam banyak kasus, kenalan dengan regresi linier dimulai. Pada saat yang sama, kalkulasi terperinci tentang bagaimana formula itu diturunkan jarang terjadi.

Misalnya, di kursus pembelajaran mesin Yandex, ketika siswa diperkenalkan dengan regularisasi, mereka menyarankan menggunakan fungsi dari perpustakaan sklearn , sementara tidak ada kata yang disebutkan tentang representasi matriks dari algoritma. Pada saat inilah beberapa pendengar mungkin ingin memahami masalah ini secara lebih rinci - menulis kode tanpa menggunakan fungsi yang sudah jadi. Dan untuk ini, pertama-tama kita harus menyajikan persamaan dengan regulator dalam bentuk matriks. Artikel ini akan memungkinkan mereka yang ingin menguasai keterampilan seperti itu. Mari kita mulai.

Baseline

Target

Kami memiliki sejumlah nilai target. Misalnya, target mungkin harga aset: minyak, emas, gandum, dolar, dll. Pada saat yang sama, dengan sejumlah nilai indikator target yang kami maksud adalah jumlah pengamatan. Pengamatan seperti itu mungkin, misalnya, harga minyak bulanan untuk tahun ini, yaitu, kita akan memiliki 12 nilai target. Kami mulai memperkenalkan notasi. Kami menetapkan setiap nilai target sebagai $$$y_i$ . Total yang kita miliki $$$n$ pengamatan, yang berarti kita bisa membayangkan pengamatan kita sebagai $$$y_1, y_2, y_3 ... y_n$ .

Regresi

Kami berasumsi bahwa ada beberapa faktor yang sampai batas tertentu menjelaskan nilai-nilai indikator target. Sebagai contoh, nilai tukar pasangan dolar / rubel sangat dipengaruhi oleh harga minyak, nilai Fed, dll. Faktor-faktor semacam itu disebut sebagai regressor. Pada saat yang sama, setiap nilai indikator target harus sesuai dengan nilai regressor, yaitu, jika kita memiliki 12 target untuk setiap bulan pada 2018, maka kita juga harus memiliki 12 regressor untuk periode yang sama. Nyatakan nilai masing-masing regresi oleh $$$x_i: x_1, x_2, x_3 ... x_n$ . Biarkan dalam kasus kami ada $$$k$ regressors (yaitu $$$k$ faktor-faktor yang mempengaruhi nilai target). Jadi regressor kami dapat direpresentasikan sebagai berikut: untuk regressor pertama (misalnya, harga minyak): $$$x_ {11}, x_ {12}, x_ {13} ... x_ {1n}$ , untuk regressor ke-2 (misalnya, suku bunga Fed): $$$x_ {21}, x_ {22}, x_ {23} ... x_ {2n}$ untuk $$$k$ "regressor: $$$x_ {k1}, x_ {k2}, x_ {k3} ... x_ {kn}$

Ketergantungan target pada regressor

Asumsikan Ketergantungan Target $$$y_i$ dari regressor " $$$i$ -th "observasi dapat diekspresikan melalui persamaan regresi linear dari bentuk:

$$

$$f (w, x_i) = w_0 + w_1 x_ {1i} + ... + w_k x_ {ki}$$

dimana $$$x_i$ - " $$$i$ nilai regressor dari 1 ke $$$n$ ,

$$$k$ - jumlah regresi dari 1 hingga $$$k$

$$$w$ - koefisien sudut yang mewakili jumlah dimana indikator target yang dihitung akan berubah rata-rata ketika regressor berubah.

Dengan kata lain, kami untuk semua orang (kecuali $$$w_0$ ) dari regressor kita menentukan koefisien "kita" $$$w$ , lalu gandakan koefisien dengan nilai-nilai dari regressor " $$$i$ -th "observasi, sebagai hasilnya kita mendapatkan perkiraan tertentu" $$$i$ "target.

Oleh karena itu, kita perlu memilih koefisien tersebut $$$w$ dimana nilai-nilai fungsi aproksimasi kami $$$f (w, x_i)$ akan ditempatkan sedekat mungkin dengan nilai target.

Estimasi kualitas fungsi aproksimasi

Kami akan menentukan estimasi kualitas fungsi aproksimasi dengan metode kuadrat terkecil. Fungsi penilaian kualitas dalam kasus ini akan mengambil bentuk berikut:

$$

$$Err = \ jumlah \ limit_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ rightarrow min$$

Kita perlu memilih nilai koefisien seperti $ w $ untuk mana nilainya $$$Err$ akan menjadi yang terkecil.

Kami menerjemahkan persamaan ke dalam bentuk matriks

Tampilan vektor

Pertama, untuk membuat hidup Anda lebih mudah, Anda harus memperhatikan persamaan regresi linier dan perhatikan bahwa koefisien pertama $$$w_0$ tidak dikalikan dengan setiap regressor. Selain itu, ketika kita menerjemahkan data ke dalam bentuk matriks, keadaan di atas akan sangat menyulitkan perhitungan. Dalam hal ini, diusulkan untuk memperkenalkan regressor lain untuk koefisien pertama $$$w_0$ dan samakan dengan satu. Atau lebih tepatnya, masing-masing " $$$i$ "nilai" dari regresi ini menyamakan dengan kesatuan - karena ketika dikalikan dengan kesatuan, tidak ada yang akan berubah dalam hal hasil perhitungan, dan dari sudut pandang aturan untuk produk matriks, siksaan kita akan berkurang secara signifikan.

Sekarang, untuk sementara, untuk menyederhanakan materi, misalkan kita hanya punya satu " $$$i$ "observasi. Lalu, bayangkan nilai-nilai dari para regresor" $$$i$ Pengamatan th sebagai vektor $$$\ vec {x_i}$ . Vektor $$$\ vec {x_i}$ memiliki dimensi $$$(k \ kali 1)$ itu adalah $$$k$ baris dan 1 kolom:

$$

$$\ vec {x_i} = \ begin {pmatrix} x_ {0i} \\ x_ {1i} \\ ... \\ x_ {ki} \ end {pmatrix} \ qquad$$

Koefisien yang diinginkan dapat direpresentasikan sebagai vektor $$$\ vec {w}$ berdimensi $$$(k \ kali 1)$ :

$$

$$\ vec {w} = \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$$

Persamaan regresi linier untuk " $$$i$ -th "observasi akan mengambil bentuk:

$$

$$f (w, x_i) = \ vec {x_i} ^ T \ vec {w}$$

Fungsi penilaian kualitas model linier akan berbentuk:

$$

$$Err = \ jumlah \ limit_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 \ rightarrow min$$

Perhatikan bahwa sesuai dengan aturan perkalian matriks, kami perlu mengubah vektor $$$\ vec {x_i}$ .

Representasi matriks

Sebagai hasil dari penggandaan vektor, kita mendapatkan nomor: $$$(1 \ kali k) \ centerdot (k \ kali 1) = 1 \ kali 1$ seperti yang diharapkan. Angka ini adalah perkiraan " $$$i$ -th "target. Tapi kita perlu memperkirakan tidak satu nilai dari target, tetapi semua. Untuk melakukan ini, kita menulis semuanya" $$$i$ matriks regresi $$$X$ . Matriks yang dihasilkan memiliki dimensi $$$(n \ kali k)$ :

$$$$ menampilkan $$ X = \ mulai {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $$ menampilkan $$ $$

Sekarang persamaan regresi linier akan berbentuk:

$$

$$f (w, X) = X \ vec {w}$$

Nyatakan nilai-nilai indikator target (semua $$$y_i$ ) per vektor $$$\ vec {y}$ dimensi $$$(n \ kali 1)$ :

$$

$$\ vec {y} = \ begin {pmatrix} y_ {0} \\ y_ {1} \\ ... \\ y_ {n} \ end {pmatrix} \ qquad$$

Sekarang kita dapat menulis dalam format matriks persamaan untuk menilai kualitas model linier:

$$

$$Err = (X \ vec {w} - \ vec {y}) ^ 2 \ rightarrow min$$

Sebenarnya, dari formula ini kita selanjutnya mendapatkan formula yang kita kenal $$$X ^ T X w = X ^ T y$

Bagaimana ini dilakukan? Kurung dibuka, diferensiasi dilakukan, ekspresi yang dihasilkan diubah, dll., Dan itulah yang akan kita lakukan sekarang.

Transformasi matriks

Perluas kurung

$$$(X \ vec {w} - \ vec {y}) ^ 2 = (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y})$

$$$= (X \ vec {w}) ^ TX \ vec {w} - \ vec {y} ^ TX \ vec {w} - (X \ vec {w}) ^ T \ vec {y} + \ vec { y} ^ T \ vec {y}$

Siapkan persamaan untuk diferensiasi

Untuk melakukan ini, kami melakukan beberapa transformasi. Dalam perhitungan selanjutnya, akan lebih nyaman bagi kita jika vektor $$$\ vec {w} ^ T$ akan disajikan pada awal setiap pekerjaan dalam persamaan.

Konversi 1

$$$\ vec {y} ^ TX \ vec {w} = (X \ vec {w}) ^ T \ vec {y} = \ vec {w} ^ TX ^ T \ vec {y}$

Bagaimana ini bisa terjadi? Untuk menjawab pertanyaan ini, lihat saja ukuran dari matriks yang dikalikan dan lihat bahwa pada output kita mendapatkan angka atau sebaliknya $$$const$ .

Kami menulis dimensi dari ekspresi matriks.

$$$\ vec {y} ^ TX \ vec {w}: (1 \ kali n) \ centerdot (n \ kali k) \ centerdot (k \ kali 1) = (1 \ kali 1) = const$

$$$(X \ vec {w}) ^ T \ vec {y}: ((n \ kali k) \ centerdot (k \ kali 1)) ^ T \ centerdot (n \ kali 1) = (1 \ kali n) \ centerdot (n \ kali 1) = (1 \ kali 1) = const$

$$$\ vec {w} ^ TX ^ T \ vec {y}: (1 \ kali k) \ centerdot (k \ kali n) \ centerdot (n \ kali 1) = (1 \ kali 1) = const$

Konversi 2

$$$(X \ vec {w}) ^ TX \ vec {w} = \ vec {w} ^ TX ^ TX \ vec {w}$

Kami menulis mirip dengan transformasi 1

$$$(X \ vec {w}) ^ TX \ vec {w}: ((n \ kali k) \ centerdot (k \ kali 1)) ^ T \ centerdot (n \ kali k) \ centerdot (k \ kali 1 ) = (1 \ kali 1) = const$

$$$\ vec {w} ^ TX ^ TX \ vec {w}: (1 \ kali k) \ centerdot (k \ kali n) \ centerdot (n \ kali k) \ centerdot (k \ kali 1) = (1 \ kali 1) = const$

Pada output, kita mendapatkan persamaan yang harus kita bedakan:
$$$Err = \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

Kami membedakan fungsi menilai kualitas model

Bedakan dengan vektor $$$\ vec {w}$ :

$$

$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}}$$

$$$(\ vec {w} ^ TX ^ TX \ vec {w}) '- (2 \ vec {w} ^ TX ^ T \ vec {y})' + (\ vec {y} ^ T \ vec {y} }) '= 0$

$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} + 0 = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

Pertanyaan mengapa $$$(\ vec {y} ^ T \ vec {y}) '= 0$ seharusnya tidak, tetapi operasi untuk menentukan turunannya dalam dua ekspresi lainnya, kami akan menganalisis secara lebih rinci.

Diferensiasi 1

Kami mengungkapkan perbedaan: $$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w})} {d \ vec {w}} = 2X ^ TX \ vec {w}$

Untuk menentukan turunan dari matriks atau vektor, Anda perlu melihat apa yang ada di dalamnya. Kami melihat:

$$$ inline $ \ vec {w} ^ T = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$\ vec {w} = \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$

$$$ sebaris $ X ^ T = \ begin {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} & x_ {11} & ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $ $$$ $ inline $ X = \ begin {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $

Nyatakan produk matriks $$$X ^ TX$ melalui matriks $$$A$ . Matriks $$$A$ persegi dan terlebih lagi, itu simetris. Properti ini akan berguna bagi kita lebih jauh, ingatlah. Matriks $$$A$ memiliki dimensi $$$(k \ kali k)$ :

$$$ inline $ A = \ begin {pmatrix} a_ {00} & a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad $ inline $ $

Sekarang tugas kita adalah dengan benar mengalikan vektor dengan matriks dan tidak mendapatkan "dua kali lima", jadi kita akan fokus dan sangat hati-hati.

$$$ sebaris $ \ vec {w} ^ TA \ vec {w} = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad \ kali \ mulai {pmatrix} a_ {00} & a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \ \ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad \ kali \ mulai {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$ sebaris $ = \ mulai {pmatrix} w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0} & ... & w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk} \ end {pmatrix} \ kali \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$= \ mulai {pmatrix} (w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0}) w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu (w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk}) w_k \ end {pmatrix} =$

$$$= w_0 ^ 2a_ {00} + w_1a_ {10} w_0 + w_ka_ {k0} w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_0a_ {0k} w_k + w_1a_ {1k} w_k + .. . + w_k ^ 2a_ {kk}$

Namun, kami mendapat ekspresi yang rumit! Bahkan, kami mendapat nomor - skalar. Dan sekarang, sudah benar-benar, kita lolos ke diferensiasi. Adalah perlu untuk menemukan turunan dari ekspresi yang diperoleh untuk setiap koefisien $$$w_0 w_1 ... w_k$ dan dapatkan vektor dimensi di output $$$(k \ kali 1)$ . Untuk berjaga-jaga, saya akan menjelaskan prosedur untuk tindakan:

1) dibedakan dengan $$$w_o$ kami mendapatkan: $$$2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k}$

2) dibedakan dengan $$$w_1$ kami mendapatkan: $$$w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ {k}$

3) dibedakan dengan $$$w_k$ kami mendapatkan: $$$w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k-1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk}$

Pada output, vektor ukuran yang dijanjikan $$$(k \ kali 1)$ :

$$

$$\ begin {pmatrix} 2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k} \\ w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ { k} \\ ... \\ ... \\ ... \\ w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k -1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + + ... + 2w_ka_ {kk} \ end {pmatrix}$$

Jika Anda melihat lebih dekat pada vektor, Anda akan melihat bahwa elemen kiri dan kanan vektor dapat dikelompokkan sedemikian rupa sehingga, sebagai hasilnya, vektor dapat dibedakan dari vektor yang disajikan $$$\ vec {w}$ ukurannya $$$(k \ kali 1)$ . Sebagai contoh $$$w_1a_ {10}$ (elemen kiri dari garis atas vektor) $$$+ a_ {01} w_1$ (elemen kanan dari garis atas vektor) dapat direpresentasikan sebagai $$$w_1 (a_ {10} + a_ {01})$ , dan $$$w_2a_ {20} + a_ {02} w_2$ - bagaimana $$$w_2 (a_ {20} + a_ {02})$ dll. di setiap baris. Kelompok:

$$

$$\ begin {pmatrix} 2w_0a_ {00} + w_1 (a_ {10} + a_ {01}) + w_2 (a_ {20} + a_ {02}) + ... + w_k (a_ {k0} + a_ { 0k}) \\ w_0 (a_ {01} + a_ {10}) + 2w_1a_ {11} + w_2 (a_ {21} + a_ {12}) + ... + w_k (a_ {k1} + a_ {1k }) \\ ... \\ ... \\ ... \\ w_0 (a_ {0k} + a_ {k0}) + w_1 (a_ {1k} + a_ {k1}) + w_2 (a_ {2k } + a_ {k2}) + ... + 2w_ka_ {kk} \ end {pmatrix}$$

Keluarkan vektor $$$\ vec {w}$ dan pada output kita dapatkan:

$$$$ tampilkan $$ \ begin {pmatrix} 2a_ {00} & a_ {10} + a_ {01} & a_ {20} + a_ {02} & ... & a_ {k0} + a_ {0k} \\ a_ {01} + a_ {10} & 2a_ {11} & a_ {21} + a_ {12} & ... & a_ {k1} + a_ {1k} \\ ... & ... & .. . & ... & ... \\ ... & ... & ... & ... & ... \\ ... & ... & ... & ... & .. . \\ a_ {0k} + a_ {k0} & a_ {1k} + a_ {k1} & a_ {2k} + a_ {k2} & ... & 2a_ {kk} \ end {pmatrix} \ kali \ mulai {pmatrix} w_0 \\ w_1 \\ ... \\ ... \\ ... \\ w_k \ end {pmatrix} \ qquad $$ menampilkan $$

Sekarang, mari kita lihat matriks yang dihasilkan. Matriks adalah jumlah dari dua matriks $$$A + A ^ T$ :

$$$$ tampilkan $$ \ begin {pmatrix} a_ {00} & a_ {01} & a_ {02} & ... & a_ {0k} \\ a_ {10} & a_ {11} & a_ {12} & ... & a_ {1k} \\ ... & ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & a_ {k2} & ... & a_ {kk} \ end {pmatrix} + \ begin {pmatrix} a_ {00} & a_ {10} & a_ {20} & ... & a_ {k0} \\ a_ {01} & a_ {11} & a_ {21} & ... & a_ {k1} \\ ... & ... & ... & ... & ... \\ a_ {0k} & a_ {1k} & a_ {2k} & ... & a_ {kk} \ end {pmatrix} \ qquad $$ menampilkan $$

Ingat bahwa sedikit lebih awal, kami mencatat satu properti penting dari matriks $$$A$ - itu simetris. Berdasarkan pada properti ini, kami dapat dengan yakin menyatakan ungkapan itu $$$A + A ^ T$ sama dengan $$$2A$ . Ini mudah untuk diverifikasi dengan mengungkapkan produk matriks demi elemen $$$X ^ TX$ . Kami tidak akan melakukan ini di sini, mereka yang ingin dapat melakukan cek sendiri.

Mari kita kembali ke ekspresi kita. Setelah transformasi kami, ternyata kami ingin melihatnya:

$$

$$(A + A ^ T) \ kali \ mulai {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = 2A \ vec {w} = 2X ^ TX \ vec {w}$$

Jadi, kami mengatasi diferensiasi pertama. Kami beralih ke ekspresi kedua.

Diferensiasi 2

$$$\ frac {d (2 \ vec {w} ^ TX ^ T \ vec {y})} {d \ vec {w}} = 2X ^ T \ vec {y}$

Mari kita pergi di sepanjang jalan yang terpukul. Ini akan jauh lebih pendek dari yang sebelumnya, jadi jangan jauh-jauh dari layar.

Kami mengungkapkan vektor elemen dan matriks:

$$$ inline $ \ vec {w} ^ T = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$ sebaris $ X ^ T = \ begin {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} & x_ {11} & ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $ $

$$$\ vec {y} = \ begin {pmatrix} y_0 \\ y_1 \\ ... \\ y_n \ end {pmatrix} \ qquad$

Untuk sementara, kami menghapus deuce dari perhitungan - itu tidak memainkan peran besar, maka kami akan mengembalikannya ke tempatnya. Kalikan vektor dengan matriks. Pertama-tama, kita mengalikan matriks $$$X ^ T$ pada vektor $$$\ vec {y}$ , di sini kita tidak memiliki batasan. Dapatkan vektor ukuran $$$(k \ kali 1)$ :

$$

$$\ begin {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

Lakukan tindakan berikut - kalikan vektor $$$\ vec {w}$ ke vektor yang dihasilkan. Pada output, angka akan menunggu kita:

$$

$$\ begin {pmatrix} w_0 (x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n) + w_1 (x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1 } y_n) \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_k (x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n) \ end {pmatrix} \ qquad$$

Kami kemudian membedakannya. Pada output kita mendapatkan vektor dimensi $$$(k \ kali 1)$ :

$$

$$\ begin {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

Apakah itu menyerupai sesuatu? Baiklah! Ini adalah produk dari matriks. $$$X ^ T$ pada vektor $$$\ vec {y}$ .

Dengan demikian, diferensiasi kedua berhasil diselesaikan.

Alih-alih sebuah kesimpulan

Sekarang kita tahu bagaimana kesetaraan muncul. $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ .

Akhirnya, kami menjelaskan cara cepat untuk mengubah formula utama.

Perkirakan kualitas model sesuai dengan metode kuadrat terkecil:
$$$\ jumlah \ limit_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ mkern 20mu = \ mkern 20mu \ jumlah \ limit_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 =$

$$$= (X \ vec {w} - \ vec {y}) ^ 2 \ mkern 20mu = \ mkern 20mu (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y}) \ mkern 20mu = \ mkern 20mu \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

Kami membedakan ekspresi yang dihasilkan:
$$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}} =$$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

$$$\ leftarrow$ Karya penulis sebelumnya - “Kami menyelesaikan persamaan regresi linier sederhana”
$$$\ rightarrow$ Karya berikutnya dari penulis - "Chewing Logistic Regression"

Sastra

Sumber internet:

1) habr.com/en/post/278513
2) habr.com/ru/company/ods/blog/322076
3) habr.com/en/post/307004
4) nabatchikov.com/blog/view/matrix_der

Buku teks, koleksi tugas:

1) Catatan kuliah tentang matematika yang lebih tinggi: kursus penuh / D.T. Ditulis - edisi ke-4. - M .: Iris Press, 2006
2) Analisis Regresi Terapan / N. Draper, G. Smith - edisi ke-2. - M .: Keuangan dan Statistik, 1986 (diterjemahkan dari bahasa Inggris)
3) Tugas untuk menyelesaikan persamaan matriks:
function-x.ru/matrix_equations.html
mathprofi.ru/deistviya_s_matricami.html