Selamat siang
Pada artikel ini saya akan mencoba untuk melihat segar pada algoritma untuk menemukan solusi umum untuk sistem persamaan linear.
Tugas yang akan kita lakukan adalah terdengar seperti ini.
Temukan solusi umum untuk sistem persamaan berikut
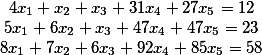
Masalah ini diselesaikan dengan mengurangi sistem awal menjadi bentuk segitiga sesuai dengan metode Gauss. Kemudian, memilih variabel bebas, solusi umum dihitung.
Saya ingin menunjukkan bagaimana seseorang dapat memecahkan sistem seperti itu dengan cara lain. Sejauh ini diketahui dan diterapkan di tempat lain, saya tidak bisa mengetahuinya. Dalam semua materi publik / populer, metode Gauss digunakan.
Saya harus mengatakan segera bahwa solusinya tentu tidak optimal (dalam hal kecepatan), karena ketika menghitung produk vektor, perlu untuk menghitung penentu matriks, dan ini entah bagaimana perhitungan matriks segitiga.
Tetapi solusinya indah dan jelas, selain itu mudah untuk melihat kriteria di mana sistem tidak memiliki solusi.
Apa inti dari teknik ini?
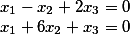
Memecahkan sistem ini sebagai produk dari dua vektor, kami dapatkan
i%20+%20(%201%20)j%20+%20(%207%20)k)
Oleh karena itu, akar dari sistem adalah sama
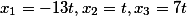
Bagi mereka yang tidak percaya, ini mudah diverifikasi dengan substitusi.
Kami menggunakan teknik ini dan mempertimbangkan bagaimana sistem tersebut diselesaikan menggunakan produk vektor.
Jadi kami memiliki sistem sumber
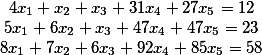
Pindahkan persyaratan gratis ke sisi kiri
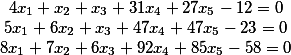
Kami mendapat 6 kolom.
Pada tahap ini, kami tidak akan memperkenalkan entitas baru dan tidak akan menggunakan konsep peringkat matriks dalam pekerjaan kami. (Tolong perlakukan saya dengan merendahkan)
Kami hanya melihat bahwa ada 3 persamaan, dan 5 variabel. Oleh karena itu, solusi umum akan menggunakan 5-3 = 2 variabel independen.
Pada langkah yang sama, kita dapat menentukan variabel mana yang akan bebas. Kami mengambil dua variabel yang akan di sebelah kanan semua dan membebaskan mereka.
Catatan: Untuk persamaan lainnya, tidak selalu menghasilkan bahwa hanya perlu mengambil koefisien kanan terakhir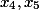
Dan sekarang dalam tiga langkah kami menentukan solusi mendasar dari sistem asli
Langkah 1. Di sini kolom terakhir adalah anggota bebas sistem.
i%20+%20(%20-162%20)j%20+%20(%20-486%20)k%20+%20(%20-81%20)l)
Langkah 2. Di sini kolom terakhir adalah koefisien untuk variabel
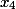
i%20+%20(%20162%20)j%20+%20(%20405%20)k%20+%20(%20-81%20)l)
Langkah 3. Di sini kolom terakhir adalah koefisien untuk variabel
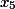
i%20+%20(%20243%20)j%20+%20(%20324%20)k%20+%20(%20-81%20)l)
Tidak perlu memberi tahu secara detail dari mana kami mendapatkan data. Saya pikir ini jelas bagi pembaca. (Siapa pun yang memecahkan sistem persamaan menggunakan metode Cramer akan menemukan fitur-fitur umum)
Yang lebih menarik adalah apa yang akan kita lakukan dengan "vektor" ini.
Bagilah dengan -81
kita mendapatkan tiga vektor berikut
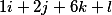
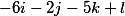
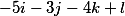
mengaturnya secara vertikal dan dengan demikian keputusan mendasar mengambil bentuk
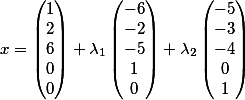
Hebat! Bukan itu ...
Untuk kriteria solvabilitas sistem persamaan tertentu, dalam kebanyakan kasus aturan Kronecker-Copelli digunakan, di sini hasil produk vektor dianalisis secara sederhana.
Jika vektor yang dihasilkan memiliki bentuk
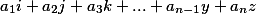
dimana 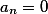 , dan di antara semua yang tersisa ada setidaknya satu non-nol, maka sistem solusi seperti itu tidak adaJika vektor yang dihasilkan memiliki semua koefisien nol, maka ini menunjukkan bahwa setidaknya salah satu persamaan adalah representasi linear dari yang lain, dan / atau salah satu variabel sebanding dengan yang lain.
, dan di antara semua yang tersisa ada setidaknya satu non-nol, maka sistem solusi seperti itu tidak adaJika vektor yang dihasilkan memiliki semua koefisien nol, maka ini menunjukkan bahwa setidaknya salah satu persamaan adalah representasi linear dari yang lain, dan / atau salah satu variabel sebanding dengan yang lain.Artikel ini adalah yang pertama, dan saya ingin mendengar komentar, kritik, harapan di alamat saya.
Algoritma dan kalkulator
dibuat kembali pada Januari 2019 , dan hanya hari ini saya memutuskan untuk menerbitkan informasi tentang Habré.
Jika Anda menerima di tim / masyarakat Anda, maka topik selanjutnya adalah
- Cara menemukan solusi umum untuk sistem persamaan Diophantine.