
Komputer kuantum dan komputasi kuantum adalah kata kunci baru yang telah ditambahkan ke ruang informasi kami bersama dengan kecerdasan buatan , pembelajaran mesin, dan istilah teknologi tinggi lainnya. Pada saat yang sama, saya tidak dapat menemukan materi di Internet yang akan menempatkan saya di kepala sebuah teka-teki yang disebut "bagaimana komputer kuantum bekerja" . Ya, ada banyak karya luar biasa, termasuk di Habré (lihat Daftar sumber daya ), komentar yang, seperti biasanya, bahkan lebih informatif dan berguna, tetapi gambar di kepala, seperti yang mereka katakan, tidak bertambah.
Dan baru-baru ini, rekan-rekan mendatangi saya dan bertanya, “Apakah Anda mengerti bagaimana komputer kuantum bekerja? Bisakah Anda memberi tahu kami? ”Dan kemudian saya menyadari bahwa masalah melipat gambar lengkap di kepala saya bukan hanya milik saya.
Akibatnya, upaya dilakukan untuk mengumpulkan informasi tentang komputer kuantum ke dalam skema logis yang konsisten di mana, pada tingkat dasar, tanpa perendaman mendalam dalam matematika dan struktur dunia kuantum , dijelaskan apa itu komputer kuantum, prinsip apa yang bekerja, dan juga masalah apa yang dihadapi ilmuwan di penciptaan dan pengoperasiannya.
Daftar isi
Penafian
(untuk isi)
Penulis bukan spesialis dalam komputasi kuantum, dan target pembaca artikel ini adalah pakar TI yang sama, bukan spesialis kuantum , yang juga ingin mengumpulkan di kepala mereka gambar yang disebut "Bagaimana komputer kuantum bekerja". Karena itu, banyak konsep dalam artikel ini sengaja disederhanakan untuk pemahaman yang lebih baik tentang teknologi kuantum di tingkat "dasar", tetapi tanpa banyak penyederhanaan dengan hilangnya konten informasi dan kecukupan .
Di beberapa tempat, artikel menggunakan bahan dari sumber lain, daftar yang diberikan di akhir artikel . Jika memungkinkan, tautan langsung dan referensi ke teks, tabel atau gambar asli dimasukkan. Jika di suatu tempat saya lupa sesuatu (atau seseorang), tulis - saya akan memperbaikinya.
Pendahuluan
(untuk isi)
Dalam bab ini, kita akan melihat secara singkat bagaimana era kuantum dimulai, yang merupakan motivasi untuk gagasan komputer kuantum, yang (negara dan perusahaan mana) saat ini merupakan pemain terkemuka dalam kliring ini, dan secara singkat berbicara tentang arah utama pengembangan komputasi kuantum.
Bagaimana semuanya dimulai
(untuk isi)

Titik referensi dari era kuantum dianggap 1900, ketika M. Planck pertama kali mengajukan hipotesis bahwa energi dipancarkan dan diserap tidak terus-menerus, tetapi dalam kuanta (bagian) terpisah. Gagasan ini diambil dan dikembangkan oleh banyak ilmuwan terkemuka pada masa itu - Bohr, Einstein, Heisenberg, Schrödinger, yang, pada akhirnya, mengarah pada penciptaan dan pengembangan ilmu pengetahuan seperti fisika kuantum . Ada banyak materi bagus tentang pengembangan fisika kuantum sebagai sains di Web.Pada artikel ini kita tidak akan membahas ini secara rinci, tetapi perlu untuk menunjukkan tanggal ketika kita memasuki era kuantum baru.
Fisika kuantum telah membawa banyak penemuan dan teknologi ke dalam kehidupan sehari-hari kita, yang tanpanya sekarang sulit untuk membayangkan dunia di sekitar kita. Misalnya, laser yang sekarang digunakan di mana-mana, dari peralatan rumah tangga (tingkat laser, dll.) Hingga sistem teknologi tinggi (laser koreksi penglihatan, halo meklon ). Adalah logis untuk mengasumsikan bahwa cepat atau lambat seseorang akan mengemukakan gagasan bahwa mengapa tidak menggunakan sistem kuantum untuk perhitungan. Dan pada tahun 1980 itu terjadi.
Wikipedia menunjukkan bahwa ilmuwan Yuri Manin adalah yang pertama mengungkapkan gagasan komputasi kuantum pada 1980. Tetapi mereka benar-benar mulai membicarakannya hanya pada tahun 1981, ketika R. Feynman yang terkenal, dalam laporannya pada konferensi pertama tentang fisika komputasi yang diadakan di Massachusetts Institute of Technology , mencatat bahwa tidak mungkin untuk memodelkan evolusi sistem kuantum pada komputer klasik dengan cara yang efektif. Dia mengusulkan model dasar komputer kuantum yang dapat melakukan simulasi seperti itu.
Ada pekerjaan seperti itu di Web di mana kronologi pengembangan komputasi kuantum dianggap lebih akademis dan detail, tetapi kita akan membahas secara singkat:
Tonggak penting dalam sejarah komputer kuantum:
Seperti yang Anda lihat, 17 tahun telah berlalu (1981-1998) dari saat ide untuk implementasi pertama di komputer dengan 2 qubit, dan 21 tahun (1998-1999) hingga saat ketika jumlah qubit meningkat menjadi 53. Butuh 11 tahun (dari 2001 hingga 2012) untuk meningkatkan hasil dari algoritma Shore (kami akan memikirkannya sedikit lebih jauh) dari angka 15 hingga 21. Juga, hanya tiga tahun yang lalu kami menyadari apa yang dibicarakan Feynman, dan belajar mensimulasikan sistem fisik paling sederhana.
Perkembangan komputasi kuantum lambat. Ilmuwan dan insinyur menghadapi tugas yang sangat kompleks, keadaan kuantum sangat pendek dan rapuh, dan untuk menjaga mereka cukup lama untuk melakukan perhitungan, kita harus membangun sarkofagi untuk puluhan juta dolar, di mana suhu dipertahankan di atas nol mutlak, dan yang dilindungi dari pengaruh eksternal. Selanjutnya kita akan membicarakan tugas dan masalah ini secara lebih rinci.
Pemain terkemuka
(untuk isi)

Slide untuk bagian ini diambil dari artikel Quantum Computer: A Big Boost Game. Kuliah di Yandex , dari seorang peneliti di Pusat Kuantum Rusia Alexei Fedorov. Saya akan membiarkan diri saya mengutip langsung:
Semua negara yang berhasil secara teknologi saat ini aktif terlibat dalam pengembangan teknologi kuantum. Sejumlah besar uang diinvestasikan dalam studi ini, program khusus untuk mendukung teknologi kuantum sedang dibuat.

Perlombaan kuantum tidak hanya melibatkan negara, tetapi juga perusahaan swasta. Secara total, Google, IBM, Intel dan Microsoft telah menginvestasikan sekitar $ 0,5 miliar dalam pengembangan komputer kuantum dalam beberapa tahun terakhir, menciptakan laboratorium besar dan pusat penelitian.
Ada banyak artikel tentang Habré dan di Web, misalnya, di sini , di sini dan di sini , di mana keadaan terkini tentang perkembangan teknologi kuantum di berbagai negara dipertimbangkan secara lebih rinci. Bagi kami sekarang, hal utama adalah bahwa semua negara dan pemain teknologi maju yang terkemuka menginvestasikan sejumlah besar uang dalam penelitian ke arah ini, yang memberi harapan untuk jalan keluar dari kebuntuan teknologi saat ini.
Arah pengembangan
(untuk isi)

Saat ini (saya mungkin salah, benar) upaya utama (dan hasil yang lebih atau kurang signifikan) untuk semua pemain terkemuka terkonsentrasi dalam dua arah:
- Komputer kuantum khusus yang ditujukan untuk menyelesaikan satu masalah spesifik tertentu, misalnya, masalah pengoptimalan. Contoh produk adalah komputer kuantum D-Wave.
- Komputer kuantum universal - yang mampu menerapkan algoritma kuantum acak (Shore, Grover, dll.). Implementasi dari IBM, Google.
Vektor pengembangan lain yang diberikan fisika kuantum kepada kita, seperti:
tentu juga dalam daftar bidang untuk penelitian, tetapi beberapa jenis hasil yang kurang lebih signifikan saat ini tampaknya ada di sana.
Selain itu, Anda dapat membaca peta jalan untuk pengembangan teknologi kuantum , baik, google " pengembangan teknologi kuantum ", misalnya, di sini , di sini dan di sini .
Dasar-dasarnya. Obyek Quantum dan Sistem Quantum
(untuk isi)

Hal yang paling penting untuk dipahami dari bagian ini adalah itu
Komputer kuantum (sebagai lawan dari yang konvensional) menggunakan objek kuantum sebagai pembawa informasi, dan objek kuantum harus terhubung ke sistem kuantum untuk melakukan perhitungan.
Apa itu objek kuantum?
Objek kuantum adalah objek microworld (dunia kuantum) yang memperlihatkan properti kuantum:
- Memiliki status tertentu dengan dua tingkat batas
- Ia berada dalam superposisi keadaannya hingga saat pengukuran
- Terlibat dengan objek lain untuk membuat sistem kuantum
- Melakukan teorema larangan klon (Anda tidak dapat menyalin status objek)
Mari kita analisis setiap properti secara lebih detail:
Memiliki status tertentu dengan dua level batas (kondisi akhir)
Contoh klasik dari dunia nyata adalah koin. Dia memiliki "sisi", yang mengambil dua tingkat batas - "elang" dan "ekor".
Ia berada dalam superposisi keadaannya hingga saat pengukuran
Melempar koin, ia terbang dan berputar. Ketika sedang berputar, tidak mungkin untuk mengatakan di mana dari level level yang berada pada "sisi" -nya. Tetapi jika kita membantingnya dan melihat hasilnya, superposisi negara segera runtuh menjadi salah satu dari dua perbatasan - "kepala" dan "ekor". Membanting koin dalam kasus kami adalah dimensi.
Terlibat dengan objek lain untuk membuat sistem kuantum
Sulit dengan koin, tetapi kami akan mencoba. Bayangkan kita melemparkan tiga koin sehingga mereka saling menempel, seperti juggling koin. Pada setiap saat waktu, tidak hanya masing-masing dari mereka berada di superposisi negara, tetapi negara-negara ini saling mempengaruhi satu sama lain (koin bertabrakan).
Melakukan teorema larangan klon (Anda tidak dapat menyalin status objek)
Sementara koin terbang dan berputar, kita sama sekali tidak dapat membuat salinan status rotasi koin mana pun yang terpisah dari sistem. Sistem hidup dengan sendirinya dan sangat cemburu untuk memberikan informasi apa pun.
Beberapa kata tentang konsep "superposisi" , di hampir semua artikel, superposisi dijelaskan sebagai "ada di semua negara pada saat yang sama", yang tentu saja benar, tetapi kadang-kadang terlalu membingungkan. Suatu superposisi keadaan juga dapat dianggap sebagai fakta bahwa pada setiap saat suatu objek kuantum memiliki probabilitas tertentu untuk runtuh ke dalam setiap level batasnya, dan secara total probabilitas ini secara alami sama dengan 1 . Lebih lanjut, ketika mempertimbangkan qubit, kita akan membahas ini lebih terinci.
Untuk koin, ini dapat dibayangkan secara visual - tergantung pada kecepatan awal, sudut lemparan, keadaan lingkungan di mana koin terbang, pada setiap saat waktu kemungkinan mendapatkan "elang" atau "ekor" berbeda. Dan, seperti yang disebutkan sebelumnya, keadaan koin terbang seperti itu dapat dibayangkan sebagai "berada dalam semua batas negara pada saat yang sama, tetapi dengan kemungkinan implementasi yang berbeda".
Objek apa pun yang memenuhi sifat-sifat di atas dan yang dapat kita buat dan kelola dapat digunakan sebagai media penyimpanan di komputer kuantum.
Sedikit lebih jauh, kita akan berbicara tentang keadaan saat ini dengan implementasi fisik qubit sebagai objek kuantum, dan apa yang sekarang digunakan para ilmuwan dalam kapasitas ini.
Jadi, properti ketiga mengatakan bahwa objek kuantum dapat terjerat untuk membuat sistem kuantum. Apa itu sistem kuantum?
Sistem kuantum adalah sistem objek kuantum terjerat dengan properti berikut:
- Sistem kuantum berada dalam superposisi dari semua keadaan yang memungkinkan dari objek yang dikandungnya
- Tidak mungkin mengetahui keadaan sistem sampai saat pengukuran
- Pada saat pengukuran, sistem mengimplementasikan salah satu varian yang mungkin dari batas negara
(dan berlari sedikit ke depan)
Konsekuensi untuk program kuantum :
- Program kuantum memiliki keadaan sistem pada input, superposisi di dalam, superposisi pada output
- Pada keluaran program setelah pengukuran, kami memiliki implementasi probabilistik dari salah satu kondisi akhir yang mungkin dari sistem (ditambah kemungkinan kesalahan)
- Setiap program kuantum memiliki arsitektur cerobong (input -> output. Tidak ada siklus, Anda tidak dapat melihat keadaan sistem di tengah proses.)
Perbandingan komputer kuantum dan konvensional
(untuk isi)

Sekarang mari kita bandingkan komputer konvensional dengan komputer kuantum.
Tingkat logika

Pada komputer biasa, ini sedikit. Sedikit deterministik terkenal melalui dan melalui. Ia dapat mengambil nilai 0 atau 1. Ia mengatasi dengan baik dengan peran unit logis untuk komputer biasa, tetapi sama sekali tidak cocok untuk menggambarkan keadaan objek kuantum , yang, seperti yang telah kami katakan, berada di alam liar dengan asumsi status batasnya .
Untuk ini, qubit diciptakan. Dalam batas negara, ia menyadari keadaan | 0> dan | 1> mirip dengan 0 dan 1, dan dalam superposisi itu mewakili distribusi probabilitas atas batas negara |0> dan |1> :
a|0> + b|1>, , a^2+b^2=1
dalam kasus ini, a dan b mewakili amplitudo dari probabilitas , dan kuadrat modul mereka mewakili probabilitas sebenarnya untuk mendapatkan nilai keadaan batas yang tepat seperti |0> dan |1>, jika qubit runtuh oleh pengukuran sekarang.
Tingkat fisik
Pada tingkat perkembangan teknologi saat ini, implementasi fisik sedikit untuk komputer biasa adalah transistor semikonduktor , untuk kuantum, seperti yang telah kita katakan, objek kuantum . Pada bagian selanjutnya, kita akan berbicara tentang apa yang sekarang digunakan sebagai pembawa fisik qubit.
Media penyimpanan
Untuk komputer biasa, ini adalah arus listrik - level tegangan, ada atau tidaknya arus, dll., Untuk kuantum - keadaan objek kuantum (arah polarisasi, putaran, dll.), Yang mungkin dalam keadaan superposisi.
Operasi
Untuk menerapkan sirkuit logis pada komputer biasa, kita semua menggunakan operasi logis yang terkenal, untuk operasi pada qubit, kita harus membuat sistem operasi yang sama sekali berbeda yang disebut gerbang kuantum . Gerbang adalah qubit tunggal dan dua qubit, tergantung pada berapa banyak qubit yang dikonversi.
Contoh gerbang kuantum:
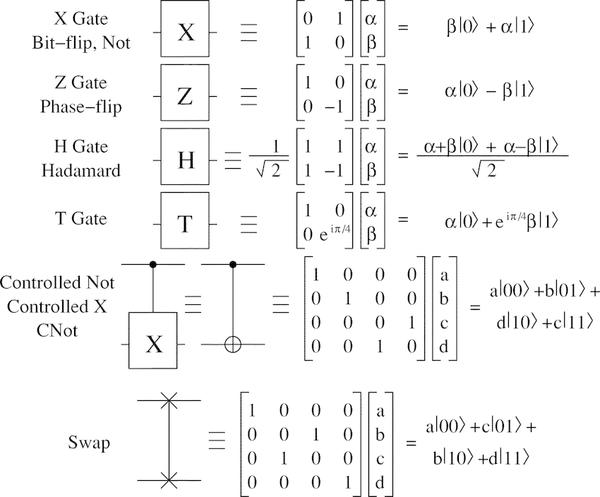
Ada konsep gerbang universal , yang cukup untuk melakukan perhitungan kuantum apa pun. Misalnya, set universal termasuk katup Hadamard, katup pergeseran fasa, katup CNOT, dan katup π⁄8. Dengan bantuan mereka, Anda dapat melakukan perhitungan kuantum apa pun pada serangkaian qubit yang sewenang-wenang.
Dalam artikel ini kita tidak akan membahas secara terperinci tentang sistem gerbang kuantum, lebih detail tentang mereka dan operasi logis pada qubit dapat dibaca, misalnya, di sini . Hal utama yang harus diingat:
- Operasi pada objek kuantum memerlukan penciptaan operator logis baru (gerbang kuantum)
- Katup kuantum adalah qubit tunggal dan dua qubit
- Ada set universal gerbang yang dengannya Anda dapat melakukan perhitungan kuantum apa pun
Interkoneksi
Satu transistor sama sekali tidak berguna bagi kita, untuk membuat perhitungan kita perlu menghubungkan banyak transistor satu sama lain, yaitu, membuat chip semikonduktor dari jutaan transistor, di mana kita sudah membangun sirkuit logika, ALU dan, pada akhirnya, mendapatkan prosesor modern dalam bentuk klasiknya.
Satu qubit juga sama sekali tidak berguna bagi kita (well, jika hanya dalam hal akademik),
untuk membuat perhitungan kita membutuhkan sistem qubit (objek kuantum)
yang, seperti telah kami katakan, diciptakan dengan melibatkan qubit di antara mereka sendiri sehingga perubahan di negara mereka terjadi secara bersamaan.
Algoritma
Algoritma standar yang diakumulasikan oleh umat manusia ke momen saat ini sama sekali tidak cocok untuk implementasi pada komputer kuantum. Ya, secara umum, dan tidak perlu. Komputer kuantum yang didasarkan pada gerbang logika atas qubit memerlukan penciptaan algoritma yang sama sekali berbeda, algoritma kuantum. Dari algoritma kuantum yang paling terkenal, tiga dapat dibedakan:
Prinsip
Dan perbedaan yang paling penting adalah prinsip kerja. Untuk komputer standar, ini adalah prinsip digital yang ditentukan secara ketat , berdasarkan fakta bahwa jika kita menetapkan beberapa kondisi awal sistem dan meneruskannya melalui algoritma yang diberikan, hasil perhitungan akan tetap sama, tidak peduli berapa kali kita menjalankan perhitungan ini. Sebenarnya, perilaku ini persis seperti yang kita harapkan dari komputer.
Komputer kuantum berjalan pada prinsip probabilitas analog . Hasil dari algoritma yang diberikan pada keadaan awal yang diberikan adalah sampel dari distribusi probabilitas implementasi akhir dari algoritma ditambah kemungkinan kesalahan.
Sifat probabilistik dari komputasi kuantum ini disebabkan oleh esensi yang sangat probabilistik dari dunia kuantum. "Tuhan tidak bermain dadu dengan alam semesta ," kata Einstein tua, tetapi semua percobaan dan pengamatan sejauh ini (dalam paradigma ilmiah saat ini) mengkonfirmasi sebaliknya.
Implementasi fisik qubit
(untuk isi)

Seperti yang telah kita katakan, qubit dapat diwakili oleh objek kuantum, yaitu objek fisik yang mengimplementasikan properti kuantum yang dijelaskan di atas. Maksudnya, secara kasar, objek fisik di mana ada dua keadaan dan kedua kondisi ini dalam keadaan superposisi dapat digunakan untuk membangun komputer kuantum.
"Jika kita bisa meletakkan atom pada dua tingkat yang berbeda dan mengendalikannya, maka inilah qubit untukmu. Jika kita bisa melakukan ini dengan ion, qubit. Itu sama dengan saat ini. Jika kita menjalankannya searah jarum jam dan berlawanan pada saat yang sama, inilah qubit. " (C)
Ada komentar yang bagus tentang artikel di mana variasi realisasi fisik qubit saat ini dipertimbangkan secara lebih rinci, tetapi kami hanya daftar yang paling terkenal dan umum:
Dari semua keragaman ini, metode pertama untuk menghasilkan qubit berdasarkan superkonduktor adalah yang paling dielaborasi. Google , IBM , Intel dan pemain terkemuka lainnya menggunakannya untuk membangun sistem mereka.
Nah, baca juga ulasan kemungkinan realisasi fisik qubit dari Andrew Daley, 2014 .
Dasar-dasarnya. Prinsip pengoperasian komputer kuantum
(untuk isi)

Bahan untuk bagian ini (tugas dan gambar) diambil dari artikel “Hampir kompleks. Cara kerja komputer kuantum . "
Jadi, mari kita bayangkan bahwa kita memiliki tugas berikut:
Ada sekelompok tiga orang: (A) ndrey, (B) olodya dan (C) bidat . Ada dua taksi (0 dan 1) .
Diketahui juga bahwa:
- (A) ndrey, (B) olodya - teman
- (A) ndrey, (C) bid'ah - musuh
- (B) olodya dan (C) bid'ah - musuh
Tugas: Tempatkan orang dengan taksi agar Max (teman) dan Min (musuh)
Nilai: L = (jumlah teman) - (jumlah musuh) untuk setiap opsi akomodasi
PENTING: Asumsikan bahwa tidak ada heuristik, tidak ada solusi optimal. Dalam hal ini, masalahnya diselesaikan hanya dengan pencarian opsi yang lengkap.
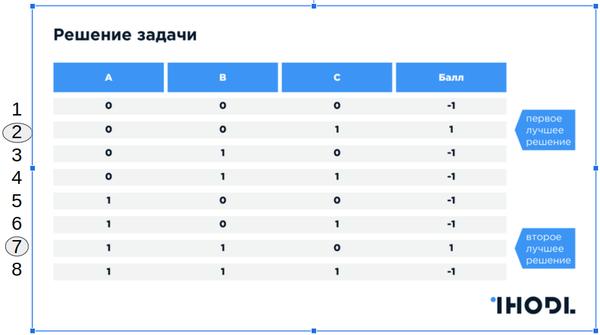
Solusi pada komputer biasa
Bagaimana mengatasi masalah ini pada komputer (atau cluster) reguler - jelas bahwa kita perlu memilah-milah semua opsi yang mungkin dalam satu lingkaran . Jika kita memiliki sistem multiprosesor, maka kita dapat memparalelkan perhitungan solusi pada beberapa prosesor dan kemudian mengumpulkan hasilnya.
Kami memiliki 2 pilihan akomodasi yang memungkinkan (taksi 0 dan taksi 1) dan 3 orang. Ruang solusi adalah 2 ^ 3 = 8 . Anda dapat melewati 8 opsi bahkan pada kalkulator, ini bukan masalah. Dan sekarang kita akan memperumit tugas - kita memiliki 20 orang dan dua bus, ruang solusinya adalah 2 ^ 20 = 1.048.576 . Tidak ada yang terlalu rumit. Mari kita meningkatkan jumlah orang sebanyak 2,5 kali - ambil 50 orang dan dua kereta, ruang keputusan sekarang 2 ^ 50 = 1,12 x 10 ^ 15 . Komputer biasa (super) sudah mulai mengalami masalah serius. Kami akan menambah jumlah orang sebanyak 2 kali, 100 orang akan memberi kami 1,2 x 10 ^ 30 opsi yang memungkinkan.
Semuanya, dalam waktu yang wajar, tugas ini tidak bisa dihitung.
Kami menghubungkan komputer super
Komputer yang paling kuat saat ini adalah nomor 1 dari Top500 , itu adalah Summit , dengan kapasitas 122 Pflops . Misalkan untuk perhitungan satu opsi, 100 operasi sudah cukup untuk kita, maka untuk menyelesaikan masalah bagi 100 orang yang kita butuhkan:
(1,2 x 10 ^ 30 100) / 122x10 ^ 15 / (60 60 24 365) = 3 x 10 ^ 37 tahun.
Seperti yang kita lihat, ketika dimensi data sumber meningkat, ruang solusi tumbuh sesuai dengan hukum kekuatan , dalam kasus umum untuk N bit kita memiliki 2 ^ N solusi yang mungkin, dengan N yang relatif kecil (100), memberi kita ruang yang tidak dapat dibaca (pada tingkat teknologi saat ini) keputusan.
Apakah ada alternatif lain? Seperti yang mungkin sudah Anda duga, ya, ada.
Tetapi sebelum kita beralih ke bagaimana dan mengapa komputer kuantum dapat secara efektif menyelesaikan masalah seperti itu, mari kita ingat sedikit tentang apa itu distribusi probabilitas . Jangan khawatir, artikel ulasan, tidak akan ada matematika keras di sini, kita akan bertahan dengan contoh klasik dengan tas dan bola.
Cukup banyak kombinasi, teori probabilitas dan eksperimen yang aneh
Ambil tas dan masukkan 1000 bola putih dan 1000 bola hitam . Kami akan melakukan percobaan - mengambil bola, menuliskan warnanya, mengembalikan bola ke tas dan mencampur bola di dalam tas.
Kami melakukan percobaan 10 kali, mengeluarkan 10 bola hitam . Mungkin? Cukup. Apakah sampel ini memberi kami konsep yang masuk akal tentang distribusi yang benar dalam tas? Jelas tidak. Yang perlu Anda lakukan adalah benar, ulangi percobaan sejuta kali dan hitung frekuensi jatuhnya bola hitam dan putih. Kami mendapatkan, misalnya, 49,95% hitam dan 50,05% putih . Dalam hal ini, struktur distribusi dari mana kami sampel sudah lebih atau kurang jelas (kami mengambil satu bola).
Hal utama yang perlu Anda pahami adalah bahwa eksperimen itu sendiri bersifat probabilistik , dengan satu sampel (bola) kami tidak mengenali struktur distribusi yang sebenarnya, kami perlu mengulangi percobaan berkali-kali dan rata-rata hasilnya.
Tambahkan 10 bola merah dan 10 bola hijau ke tas kami (kesalahan). Ulangi percobaan 10 kali. Di tarik 5 merah dan 5 hijau . Mungkin? Ya Kita dapat mengatakan sesuatu tentang distribusi yang sebenarnya - Tidak. Apa yang perlu dilakukan - yah, Anda mengerti.
Untuk mendapatkan pemahaman tentang struktur distribusi probabilitas, perlu untuk berulang kali sampel hasil individu dari distribusi ini dan rata-rata hasilnya.
Kami menghubungkan teori dengan praktik
Sekarang, alih-alih bola hitam dan putih, mari kita ambil bola biliar dan masukkan ke dalam tas 1000 bola dengan nomor 2, 1000 dengan nomor 7 dan 10 bola dengan nomor lainnya . Bayangkan seorang eksperimen yang terlatih dalam langkah-langkah sederhana (mendapatkan bola, menuliskan nomornya, memasukkan bola kembali ke dalam tas, mencampur bola di dalam tas) dan dia melakukannya dalam 150 mikrodetik. Nah, eksperimen seperti itu pada alat bantu (bukan iklan narkoba !!!). Kemudian dalam 150 detik dia akan dapat melakukan percobaan kami 1 juta kali dan memberi kami hasil rata-rata.
Mereka duduk eksperimen, memberikan tas, berbalik, menunggu 150 detik - menerima:
angka 2 - 49,5%, angka 7 - 49,5%, angka yang tersisa dalam jumlah - 1%.
Ya, benar, tas kami adalah komputer kuantum dengan algoritma yang memecahkan masalah kami , dan bola adalah solusi yang memungkinkan. Karena ada dua solusi yang tepat, komputer kuantum akan memberi kita kemungkinan yang sama salah satu dari kemungkinan solusi ini, dan 0,5% (10/2000) kesalahan , yang akan kita bicarakan nanti.
Untuk mendapatkan hasil komputer kuantum, Anda harus menjalankan algoritme kuantum berulang kali pada set data input yang sama dan rata-rata hasilnya.
Skalabilitas komputer kuantum
Sekarang mari kita bayangkan bahwa untuk masalah di mana 100 orang berpartisipasi (kita ingat ruang keputusan ini 2 ^ 100 ), hanya ada dua solusi yang benar. Kemudian, jika kita mengambil 100 qubit dan menulis algoritma yang menghitung fungsi tujuan kita (L, lihat di atas) di atas qubit ini, maka kita mendapatkan tas yang berisi 1000 bola dengan jumlah jawaban benar pertama, 1000 dengan jumlah jawaban benar kedua dan 10 bola dengan nomor lain. Dan eksperimen kami dalam 150 detik yang sama akan memberi kami perkiraan distribusi probabilistik dari jawaban yang benar .
Waktu eksekusi algoritma kuantum (dengan beberapa asumsi) dapat dianggap konstan O (1) sehubungan dengan dimensi ruang solusi (2 ^ N).
Dan justru ini properti komputer kuantum - keteguhan waktu eksekusi sehubungan dengan kompleksitas ruang keputusan yang tumbuh sesuai dengan hukum kekuasaan adalah kuncinya.
Dunia Qubit dan paralel
Bagaimana ini bisa terjadi? Apa yang memungkinkan komputer kuantum membuat perhitungan begitu cepat? Ini semua tentang sifat kuantum qubit.
Begini, kami mengatakan bahwa qubit sebagai objek kuantum menyadari salah satu dari dua keadaannya ketika diamati , tetapi dalam "alam yang hidup" ia berada dalam superposisi keadaan , yaitu, ia berada di kedua batas negara pada saat yang sama (dengan beberapa kemungkinan).
Ambil (A) Ndrey dan bayangkan kondisinya (di mana kendaraan itu 0 atau 1) sebagai qubit. Kemudian kita memiliki (dalam ruang kuantum) dua dunia paralel , dalam satu (A) duduk di taksi 0, di dunia lain - di taksi 1. Pada saat yang sama dalam dua taksi , tetapi dengan beberapa peluang menemukannya di masing-masing ketika mengamati.
Ambil (B) olod dan bayangkan negaranya sebagai qubit. Dua dunia paralel lainnya muncul. Tetapi sementara pasangan dunia ini (A) dan (B) tidak berinteraksi dengan cara apa pun. Apa yang perlu dilakukan untuk membuat sistem yang terhubung ? Itu benar, Anda perlu menghubungkan (membingungkan) qubit ini. Kami mengambil dan membingungkan (A) dengan (B) - kami memperoleh sistem kuantum dari dua qubit (A, B), yang mengimplementasikan empat dunia paralel yang saling tergantung di dalam dirinya sendiri. Tambahkan (C) erge dan dapatkan sistem tiga qubit (ABC), yang mengimplementasikan delapan dunia paralel yang saling tergantung .
Inti dari komputasi kuantum (implementasi rantai gerbang kuantum di atas sistem qubit berpasangan) adalah kenyataan bahwa perhitungan berlangsung di semua dunia paralel secara bersamaan.
Dan tidak peduli berapa banyak dari mereka yang kita miliki, 2 ^ 3 atau 2 ^ 100, algoritma kuantum akan dieksekusi dalam waktu yang terbatas di semua dunia paralel ini dan memberikan kita hasilnya, yang merupakan sampel dari distribusi probabilitas dari jawaban-jawaban dari algoritma.
Untuk pemahaman yang lebih baik, kita dapat membayangkan bahwa komputer kuantum pada tingkat kuantum mulai 2 ^ N proses keputusan paralel , masing-masing bekerja pada satu opsi yang memungkinkan, kemudian mengumpulkan hasil kerja - dan memberi kita jawaban dalam bentuk superposisi solusi (distribusi probabilitas jawaban), dari yang kami sampel satu kali setiap kali (dalam setiap percobaan).
Ingat waktu yang diperlukan untuk percobaan kami (150 μs) untuk melakukan percobaan, ini akan berguna sedikit lebih jauh ketika kita berbicara tentang masalah utama komputer kuantum dan waktu dekoherensi.
Algoritma kuantum
(untuk isi)
Seperti yang telah disebutkan, algoritma konvensional yang didasarkan pada logika biner tidak berlaku untuk komputer kuantum yang menggunakan logika kuantum (gerbang kuantum). Baginya, ia harus membuat yang baru yang memanfaatkan sepenuhnya potensi yang melekat dalam sifat kuantum komputasi.
Algoritma yang paling terkenal saat ini adalah:
Tidak seperti yang klasik, komputer kuantum tidak universal.
Sejauh ini, hanya sejumlah kecil algoritma kuantum telah ditemukan. (C)
Berkat oxoron untuk tautan ke Kebun Binatang Algoritma Quantum , tempat di mana, menurut penulis ( Stephen Jordan ), perwakilan terbaik dari dunia algoritme-kuantum dikumpulkan dan terus berkumpul.
Pada artikel ini kami tidak akan menganalisis algoritma kuantum secara terperinci, ada banyak materi bagus di Web untuk tingkat kompleksitas apa pun, tetapi Anda masih perlu membahas secara singkat tiga yang paling terkenal.
Algoritma Shore.
(untuk isi)
Algoritma kuantum yang paling terkenal adalah algoritma Shor (ditemukan pada tahun 1994 oleh ahli matematika Inggris Peter Shor ), yang bertujuan memecahkan masalah penguraian angka menjadi faktor prima (masalah faktorisasi, logaritma diskrit).
Algoritma ini digunakan sebagai contoh ketika mereka menulis bahwa sistem perbankan dan kata sandi Anda akan segera diretas. Menimbang bahwa panjang kunci yang digunakan saat ini tidak kurang dari 2048 bit, waktu untuk tutup belum tiba.
Sampai saat ini, hasilnya lebih dari sederhana. Hasil faktorisasi terbaik menggunakan algoritma Shore adalah angka 15 dan 21 , yang jauh lebih sedikit dari 2048 bit. Untuk hasil yang tersisa dari tabel, algoritma perhitungan yang berbeda digunakan, tetapi bahkan hasil terbaik menurut algoritma ini (291311) masih jauh dari aplikasi nyata.
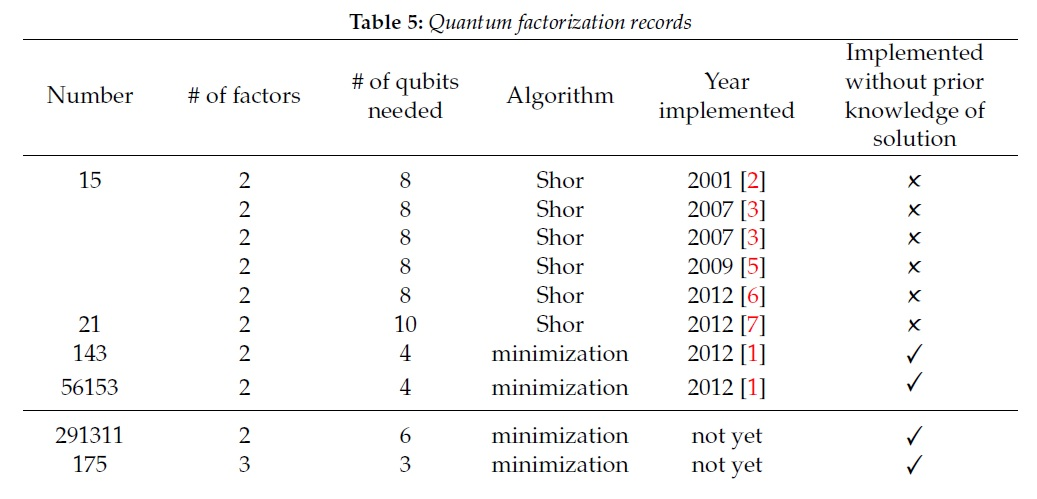
Anda dapat membaca lebih lanjut tentang algoritma Shore, misalnya, di sini . Tentang implementasi praktis - di sini .
Salah satu perkiraan kompleksitas dan daya saat ini yang diperlukan untuk memfaktorkan angka 2048-bit adalah komputer dengan 20 juta qubit . Kami tidur nyenyak.
Algoritma Grover
(untuk isi)
Algoritma Grover adalah algoritma kuantum untuk menyelesaikan masalah enumerasi, yaitu, menemukan solusi untuk persamaan F(X) = 1 , di mana F adalah fungsi Boolean dari n variabel. Itu diusulkan oleh ahli matematika Amerika Lov Grover pada tahun 1996 .
Algoritma Grover dapat digunakan untuk menemukan median dan rata - rata aritmatika dari seri angka. Selain itu, dapat digunakan untuk memecahkan masalah NP-lengkap dengan mencari di antara banyak solusi yang mungkin. Ini dapat menyebabkan peningkatan kecepatan yang signifikan dibandingkan dengan algoritma klasik, meskipun tanpa memberikan " solusi polinom " secara umum . (C)
Anda dapat membaca lebih lanjut di sini , atau di sini . Ada juga penjelasan yang baik tentang algoritma pada contoh kotak dan bola, tetapi, sayangnya, karena alasan di luar kendali saya, situs ini tidak terbuka untuk saya dari Rusia. Jika situs Anda juga diblokir, maka ini adalah perasan singkat:
Algoritma Grover. Bayangkan Anda memiliki N potong kotak tertutup bernomor. Mereka semua kosong kecuali yang ada di mana bola berada. Tugas Anda: untuk mengetahui nomor kotak tempat bola itu berada (angka yang tidak dikenal ini sering dilambangkan dengan huruf w).

Bagaimana cara mengatasi masalah ini? , , . , ? N/2. , 100 , 100 , , .
. , , (Oracle). — « 732», « 732 ». , , « , »
, , , : N SQRT(N) !
.
-
( )
— ( — ) — [ ]( https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%BE%D0%B2%D1%8B%D0%B9 %D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC), 1992 , , . _
— , F(x1, x2, … xn) ( 0, 1 ) ( 0, 1). , , . ()
. :
( — ) , . , . : «» «» – , «», «» — . , , – . ()
( )

, . ( ) :
“ ”, .
:
( )
N+1 .
, , ( ) . , , — .
, (-273.14 ) - , () .
, , .
.
, . — IBM IBM Q System One Google Sycamore . , (2) 200 .
Sycamore, — 1 200 , — 130 . 150 . ? .
?
, 150 N — .
:
150 . — .
...
( )

, , 100% , - . , . :
, , , . , , . , , , .
— () , , , . — “ ?” — 5050, .
, ( ) - . . N 1 .
— . , 100 , 80 , 20.
— , . .
. , — IBM IBM Q System One Google Sycamore :
— . 1-Fidelity. , 2- .
2016 NQIT .
( )

, . () , , .
1- , , 12-, , , . , , , , .
, , , “ ” “” . .
:
, , . , , . - , .
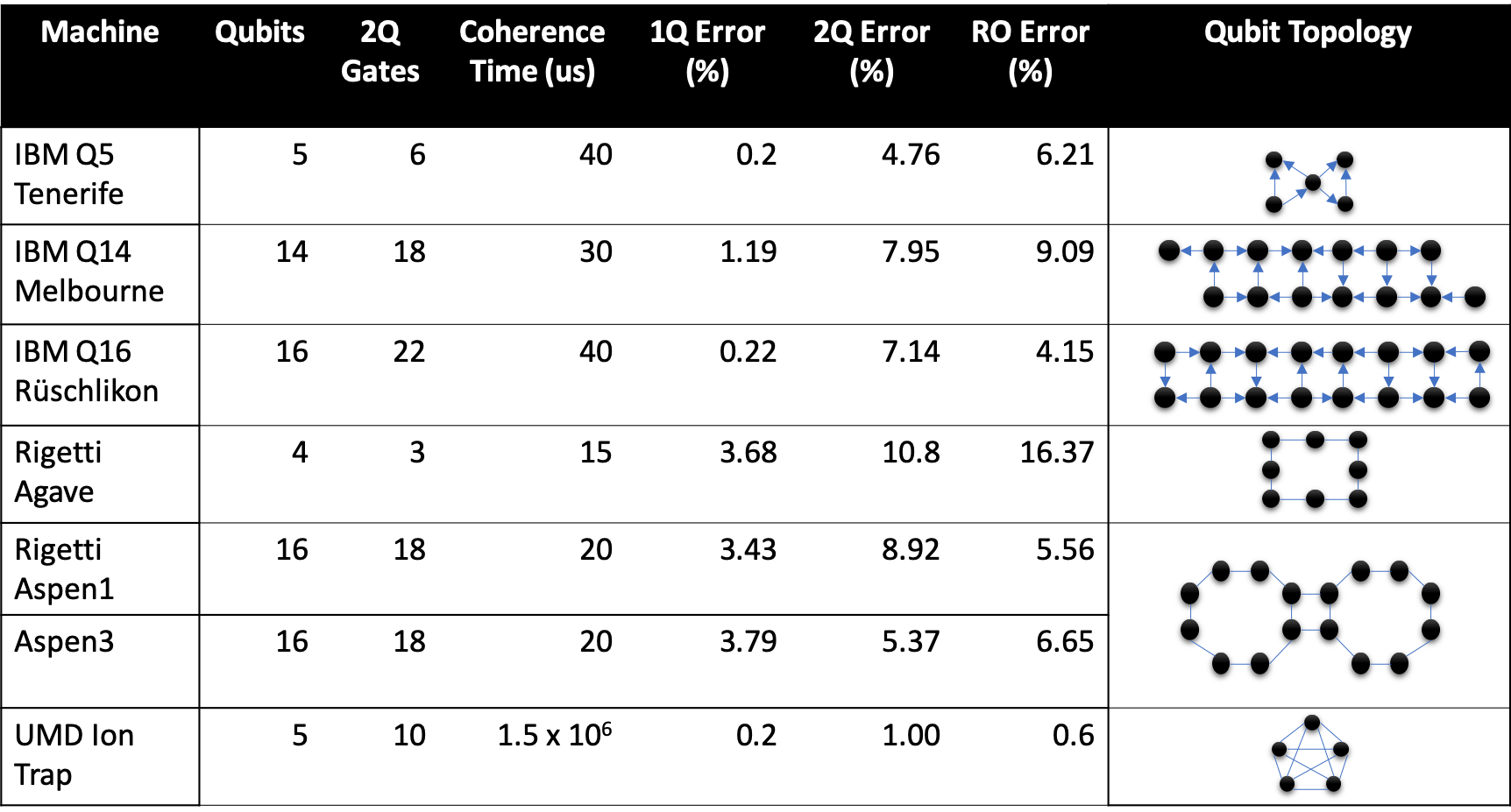
:
( )
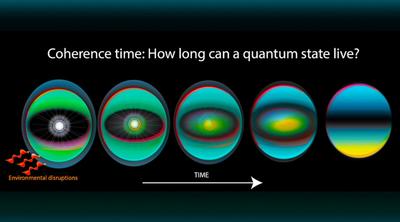
— . 150 :
, 0.5 , :
We measure a qubit coherence time in excess of 0.5 s, and with magnetic shielding we expect this to improve to be longer than 1000 s
, , .
, , , .
, , , 1 4 1 6.
( )
, :
, , ( ) , . ( ), , .
D-Wave
( )

2000- D-Wave 2000Q. : D-Wave Systems
Google 53- , D-Wave, , . , 53 , 2048 ? ...
( ):
D-Wave ( ), , .
, , , (, ), Scott Aaronson . , ,
D-Wave. , 2014 IBM , D-Wave . , 2015 Google NASA , , , . Google , , .
, D-Wave, . , . , — . , D-Wave ASIC .
( )
. , :
- , 232 264 (8-16 )
- N 2^N , .. 2^(3+N) 32- 2^(4+N) 64- .
- N 2^N x 2^N
:
()
, Summit ( Top-1 Top-500 ) 2.8 .
— 49 ( Sunway Taihu Light )
.
. :
— 49 - 39 "" ( ) 2^63 — 4 4
50+ . - Google 53- .
.
( )

:
́ ́ — , .
, , , , , . .
, “ ”. , 50+ , , , . .
, . , Google, Sycamore .
Google
( )

54- Sycamore
, 2019 Google Nature « ». 54- «Sycamore».
Sycamore 54- , 53-. , , 54- , . , 53- .
, .
IBM , Google . , 2,5 , , . .
, , Scott Aaronson . Scott's Supreme Quantum Supremacy FAQ! , . FAQ, , , .
Google? , :
, , , . : (.. 1- 2- — — , 20, 2D n=50-60 ). , 0, {0,1}, n- () . , , .
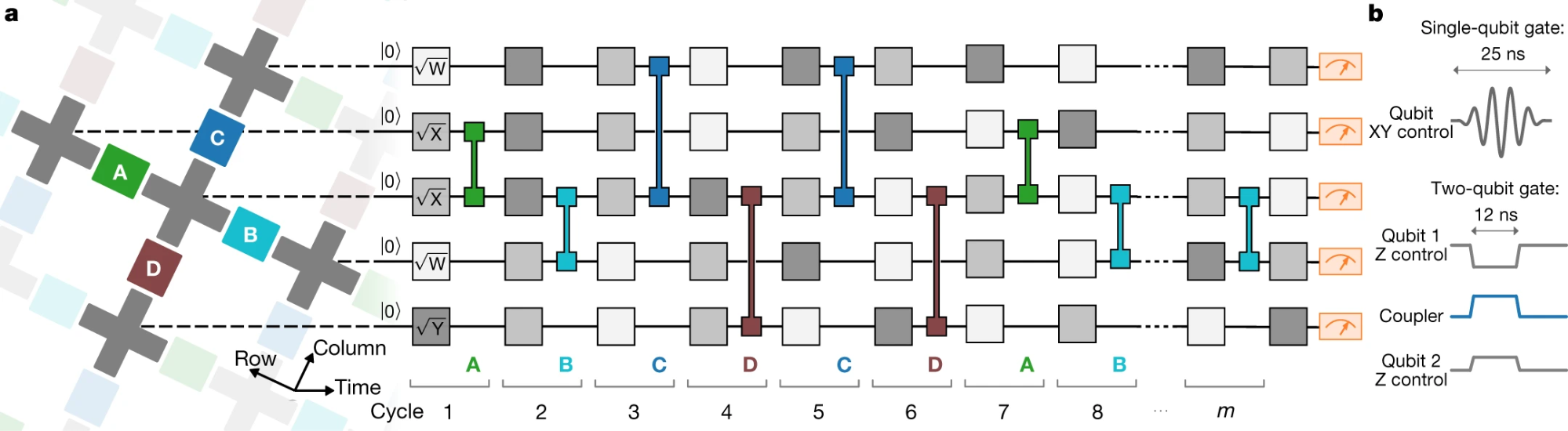
:
Google 53- , .
— Google , , , , , . , 2048- .
Ringkasan
( )

— , .
(-) :
:
:
:
( ), , - , .
— , , . .
Kesimpulan
( )
, , , , D-Wave Google .
(, , ..) , , , , .. , .
, - .
() Kruegger
( )

@Oxoron , “ ”
@a5b - “ ” , , .
, .
( )

[The National Academies Press]