Memvisualisasikan penarik aneh di Plotly adalah sebuah mahakarya

Puisi adalah suku kata yang sangat indah dan sering dipikirkan yang tidak kita gunakan dalam kehidupan sehari-hari, tetapi suka menikmatinya seperti itu. Hal yang sama dapat dikatakan tentang matematika. Dalam film "Pi", protagonis menyebut matematika "bahasa alamiah", dan dalam film "Games of the Mind" protagonis menyebutnya sebagai "jenis seni khusus." Dalam kehidupan sehari-hari, kita bisa sepenuhnya melupakannya.

Penampilan penarik aneh tidak biasa dan menarik bahkan dalam dimensi dua dimensi. Plotly memungkinkan Anda membangunnya dalam tiga dimensi, dan membuatnya sangat mudah untuk mendapatkan model 3D yang bisa Anda "pelintir" dan melaluinya Anda bisa "terbang" - rasa "sentuhan".

Bagaimana semuanya dimulai

Semuanya berawal sejak lama, di suatu tempat di tahun 2007 di universitas saya berkenalan dengan teori swasusun dan untuk pertama kalinya saya melihat si penarik Lorenz, ilustrasi hitam-putihnya dalam sebuah buku. Kemudian bagiku terasa terlalu aneh bahwa sesuatu dapat bergerak di sepanjang lintasan yang tidak biasa itu. Bahkan orang asing bagi saya sepertinya gagasan bahwa hampir semua hal di dunia ini dapat dijelaskan oleh satu teori.

Secara umum, semuanya seperti biasa - pandangan dunia saya telah berubah, hidup terus berjalan, waktu berlalu. Dan sekarang, baru-baru ini, saya menemukan tautan dan melihat ini:


Gambar diambil dari chaoticatmospheres.com

"Cantik." Pikirku. Gagasan bahwa semua ini dapat dibangun di Matplotlib juga terlintas, tetapi saya sudah tahu sebelumnya bahwa tidak ada yang spektakuler yang akan berhasil. Dan baru-baru ini, hanya dua minggu yang lalu, saya bertemu Plotly dan segera menyadari bahwa ada sesuatu yang bisa terjadi.

Upaya pertama untuk membangun segera gagal. Ternyata rumus pada beberapa gambar "Galeri penarik aneh" mengandung kesalahan. Namun, penulis galeri dengan jujur ​​memperingatkan bahwa ia bukan ahli matematika, seperti penulis artikel ini.

"Google" singkat memungkinkan untuk menemukan kode ini, yang ternyata sangat berguna, dan diciptakan oleh Michael Tyka. Orang yang luar biasa ini membuat plug-in untuk Blender, memungkinkan Anda membuat model (!) Dari 60 penarik. Bahkan, mereka dapat dicetak pada printer 3D, dan mengingat bahwa ada teknologi pencetakan lilin, cukup mudah untuk mendapatkan cetakan untuk casting di perunggu.

Kode visualisasi

Nah, selain menjadi ahli matematika amatir, saya juga seorang programmer amatir. Jadi jangan menilai ketat untuk kualitas kode.

################################ ###   ### ################################ import numpy as np from scipy.integrate import odeint import plotly.graph_objects as go ################################## ###    ### ################################## #  : def LorenzMod1(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -alpha*x + y*y - z*z + alpha*xi y_dt = x*(y - beta*z) + delta z_dt = -z + x*(beta*y + z) return x_dt, y_dt, z_dt #     : alpha = 0.1 beta = 4 xi = 14 delta = 0.08 x_0, y_0, z_0 = 0, 1, 0 #      #  : tmax, n = 100, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LorenzMod1, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) X, Y, Z = fT ####################### ###  ### ####################### # ,    : c = np.linspace(0, 1, n) #    : DATA = go.Scatter3d(x=X, y=Y, z=Z, line=dict(color= c, width=3, #   : # Greys,YlGnBu,Greens,YlOrRd,Bluered,RdBu, # Reds,Blues,Picnic,Rainbow,Portland,Jet, # Hot,Blackbody,Earth,Electric,Viridis,Cividis. colorscale="Cividis"), #   : mode='lines') fig = go.Figure(data=DATA) #   : fig.update_layout(width=1000, height=1000, margin=dict(r=10, l=10, b=10, t=10), #   : paper_bgcolor='rgb(0,0,0)', scene=dict(camera=dict(up=dict(x=0, y=0, z=1), eye=dict(x=0, y=1, z=1)), #   #     : aspectratio = dict(x=1, y=1, z=1), # ,    "aspectratio" aspectmode = 'manual', #  : xaxis=dict(visible=False), yaxis=dict(visible=False), zaxis=dict(visible=False) ) ) ###################### #!!  !!# ###################### fig.show() 

Akibatnya, model 3D dari penarik aneh bernama Lorenz Mod 1 akan muncul:


Harus segera dicatat bahwa untuk menyelesaikan sistem persamaan diferensial, fungsi odeint dipilih dari modul SciPy, yang bagi saya merupakan jalan keluar termudah dan tercepat untuk membuat kode kerja. Namun, semua persamaan dapat diselesaikan dengan metode Euler yang biasa.

Untuk menunjukkan koefisien dalam kode, karena kebiasaan, saya menggunakan nama-nama huruf Yunani yang diadopsi dalam LaTeX. Saat bekerja dengan notebook Jupyter, ini terkadang sangat berguna, karena formula dapat dengan cepat menjadi kode, dan kode dapat dengan cepat berubah menjadi formula.

Jika Anda baru mengenal ekosistem Python, tetapi Anda ingin kode dijamin berjalan, yang terbaik adalah menginstal versi terbaru distribusi Python Anaconda , dan paket Plotly melalui konda adalah pengelola paket distribusi bawaan.

Mengingat banyaknya penarik aneh, tampaknya mustahil untuk membangun semuanya. Karena itu, dalam artikel ini saya hanya akan memberikan yang paling menarik dari yang berhasil saya buat.

Penarik Chen-Lee

 #  : def ChenLee(XYZ, t, alpha, beta, delta): x, y, z = XYZ x_dt = alpha*x - y*z y_dt = beta*y + x*z z_dt = delta*z + x*y/3 return x_dt, y_dt, z_dt #     : alpha = 5 beta = -10 delta = -0.38 x_0, y_0, z_0 = 1, 1, 1 #      #  : tmax, n = 200, 30000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChenLee, (x_0, y_0, z_0), t, args=(alpha, beta, delta)) 

Penarik Chua

 #  : def ChuaAttractor(XYZ, t, alpha, beta, zeta, delta): x, y, z = XYZ h = zeta*x + (0.5*(delta - zeta))*(np.abs(x + 1) - np.abs(x - 1)) x_dt = alpha*(-x + y - h) y_dt = x - y + z z_dt = -beta*y return x_dt, y_dt, z_dt #     : alpha = 15.6 beta = 25.58 zeta = -5/7 delta = -8/7 x_0, y_0, z_0 = 1.8, -0.7, -2.85 #      #  : tmax, n = 200, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChuaAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta)) 

Penarik Coullet

 #  : def Coullet(XYZ, t, alpha, beta, zeta, delta): x, y, z = XYZ x_dt = y y_dt = z z_dt = alpha*x + beta*y + zeta*z + delta*x**3 return x_dt, y_dt, z_dt #     : alpha = 0.8 beta = -1.1 zeta = -0.4 delta = -1 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 200, 20000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Coullet, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta)) 

Penarik Dadras

 #  : def DadrasAttractor(XYZ, t, rho, sigma, tau, zeta, epsilon): x, y, z = XYZ x_dt = y - rho*x + sigma*y*z y_dt = tau*y - x*z + z z_dt = zeta*x*y - epsilon*z return x_dt, y_dt, z_dt #     : rho = 3 sigma = 2.7 tau = 1.7 zeta = 2 epsilon = 9 x_0, y_0, z_0 = 0.1, 0.03, 0 #      #  : tmax, n = 220, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(DadrasAttractor, (x_0, y_0, z_0), t, args=(rho, sigma, tau, zeta, epsilon)) 

Penarik Li Dequan

 #  : def DequanLi(XYZ, t, alpha, beta, delta, epsilon, rho, xi): x, y, z = XYZ x_dt = alpha*(y - x) + delta*x*z y_dt = rho*x + xi*y -x*z z_dt = beta*z + x*y - epsilon*x*x return x_dt, y_dt, z_dt #     : alpha = 40 beta = 1.833 delta = 0.16 epsilon = 0.65 rho = 55 xi = 20 x_0, y_0, z_0 = 0.01, 0, 0 #      #  : tmax, n = 50, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(DequanLi, (x_0, y_0, z_0), t, args=(alpha, beta, delta, epsilon, rho, xi)) 

Penarik Keuangan

 #  : def FinanceAttractor(XYZ, t, alpha, beta, zeta): x, y, z = XYZ x_dt = (1/beta - alpha)*x + x*y + z y_dt = -beta*y - x**2 z_dt = -x - zeta*z return x_dt, y_dt, z_dt #     : alpha = 0.001 beta = 0.2 zeta = 1.1 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 300, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(FinanceAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta)) 

Penarik Empat Sayap

 #  : def FourWing(XYZ, t, alpha, beta, zeta): x, y, z = XYZ x_dt = alpha*x + y + y*z y_dt = -x*z + y*z z_dt = -z - zeta*x*y + beta return x_dt, y_dt, z_dt #     : alpha = 5 beta = 16 zeta = 2 x_0, y_0, z_0 = 1, -1, 1 #      #  : tmax, n = 100, 60000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(FourWing, (x_0, y_0, z_0), t, args=(alpha, beta, zeta)) 

Penarik Hadley

 #  : def HadleyAttractor(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -y*y - z*z - alpha*x + alpha*xi y_dt = x*y - beta*x*z - y + delta z_dt = beta*x*y + x*zz return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = 4 xi = 8 delta = 1 x_0, y_0, z_0 = 0.39, -1, 0 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(HadleyAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) 

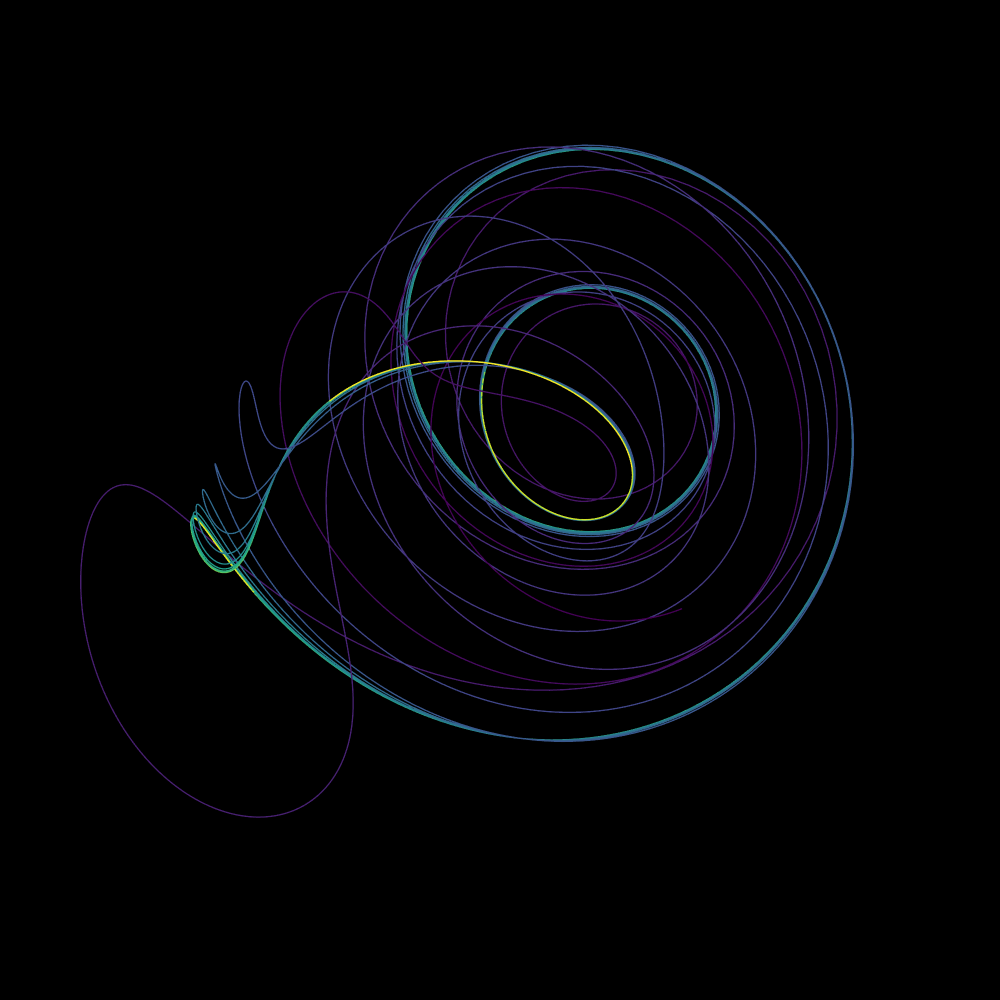
Penarik Halvorsen

 #  : def HalvorsenAttractor(XYZ, t, alpha): x, y, z = XYZ x_dt = -alpha*x - 4*y - 4*z - y*y y_dt = -alpha*y - 4*z - 4*x - z*z z_dt = -alpha*z - 4*x - 4*y - x*x return x_dt, y_dt, z_dt #     : alpha = 1.4 x_0, y_0, z_0 = -5, 0, 0 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(HalvorsenAttractor, (x_0, y_0, z_0), t, args=(alpha,)) 

Penarik Liu-Chen

 #  : def LiuChen(XYZ, t, alpha, beta, sigma, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*y + beta*x + sigma*y*z y_dt = delta*y - z + epsilon*x*z z_dt = xi*z - x*y return x_dt, y_dt, z_dt #     : alpha = 2.4 beta = -3.75 sigma = 14 delta = -11 epsilon = 4 xi = 5.58 x_0, y_0, z_0 = 1, 3, 5 #      #  : tmax, n = 55, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LiuChen, (x_0, y_0, z_0), t, args=(alpha, beta, sigma, delta, epsilon, xi)) 

Penarik Lorenz Mod 2

 #  : def LorenzMod2(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -alpha*x + y**2 -z**2 + alpha*xi y_dt = x*(y - beta*z) + delta z_dt = -z + x*(beta*y + z) return x_dt, y_dt, z_dt #     : alpha = 0.9 beta = 5 xi = 9.9 delta = 1 x_0, y_0, z_0 = 5, 5, 5 #      #  : tmax, n = 50, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LorenzMod2, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) 

Penarik Chaotic Chua yang Dimodifikasi

 #  : def ChuaModified(XYZ, t, alpha, beta, gamma, delta, zeta): x, y, z = XYZ h = -delta*np.sin((np.pi*x)/(2*gamma)) x_dt = alpha*(y - h) y_dt = x - y + z z_dt = -beta*y return x_dt, y_dt, z_dt #     : alpha = 10.82 beta = 14.286 gamma = 1.3 delta = 0.11 zeta = 7 x_0, y_0, z_0 = 1, 1, 0 #      #  : tmax, n = 200, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChuaModified, (x_0, y_0, z_0), t, args=(alpha, beta, gamma, delta, zeta)) 

Penarik Newton Leipnik

 #  : def NewtonLeipnik(XYZ, t, alpha, beta): x, y, z = XYZ x_dt = -alpha*x + y + 10*y*z y_dt = -x - 0.4*y + 5*x*z z_dt = beta*z - 5*x*y return x_dt, y_dt, z_dt #     : alpha = 0.4 beta = 0.175 x_0, y_0, z_0 = 0.349, 0, -0.16 #      #  : tmax, n = 300, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(NewtonLeipnik, (x_0, y_0, z_0), t, args=(alpha, beta)) 

Penarik Hidung-Hoover

 #  : def NoseHoover(XYZ, t, alpha): x, y, z = XYZ x_dt = y y_dt = -x + y*z z_dt = alpha - y*y return x_dt, y_dt, z_dt #     : alpha = 1.5 x_0, y_0, z_0 = 1, 0, 0 #      #  : tmax, n = 150, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(NoseHoover, (x_0, y_0, z_0), t, args=(alpha,)) 

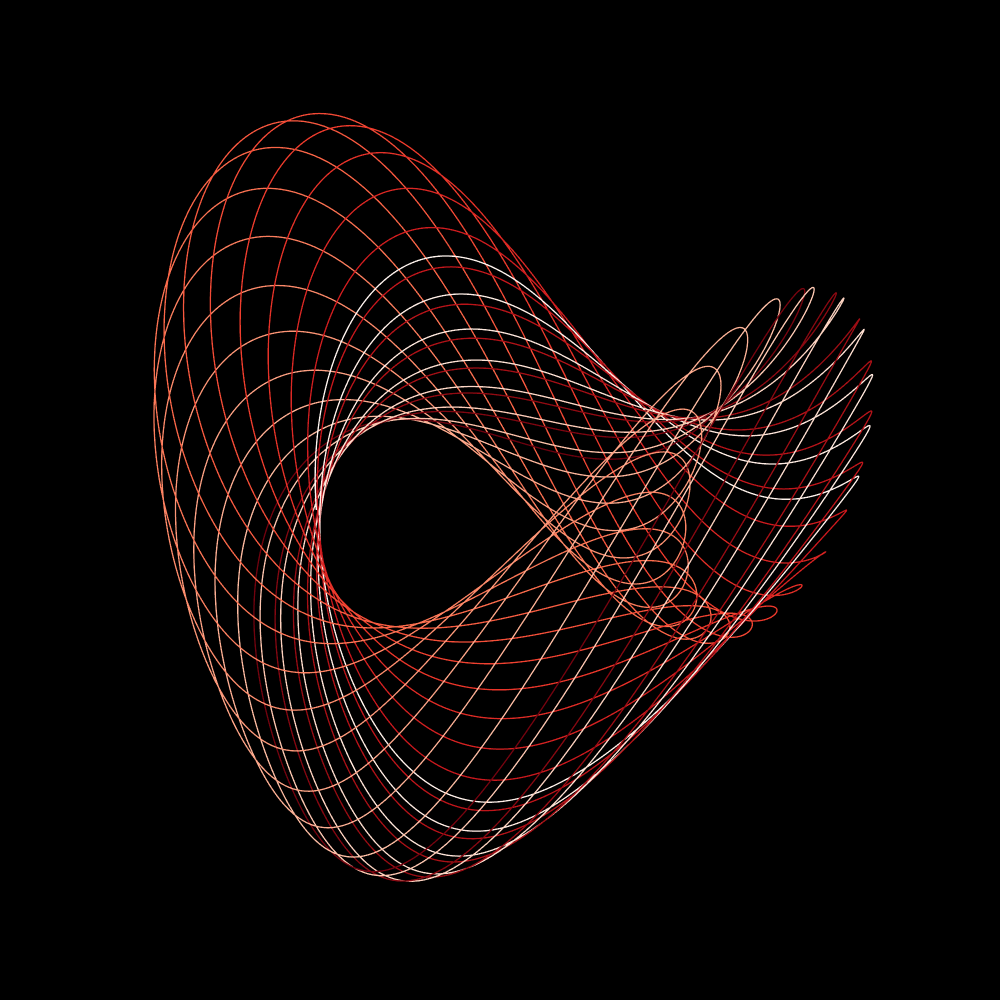
Penarik Roessler

 #  : def Roessler(XYZ, t, alpha, beta, sigma): x, y, z = XYZ x_dt = -(y + z) y_dt = x + alpha*y z_dt = beta + z*(x - sigma) return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = 0.2 sigma = 5.7 x_0, y_0, z_0 = 1, 1, 1 #      #  : tmax, n = 300, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Roessler, (x_0, y_0, z_0), t, args=(alpha, beta, sigma)) 

Penarik Sakarya

 #  : def SakaryaAttractor(XYZ, t, alpha, beta): x, y, z = XYZ x_dt = -x + y + y*z y_dt = -x - y + alpha*x*z z_dt = z - beta*x*y return x_dt, y_dt, z_dt #     : alpha = 0.4 beta = 0.3 x_0, y_0, z_0 = 1, -1, 1 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(SakaryaAttractor, (x_0, y_0, z_0), t, args=(alpha, beta)) 

Penarik Thomas

 #  : def Thomas(XYZ, t, beta): x, y, z = XYZ x_dt = -beta*x + np.sin(y) y_dt = -beta*y + np.sin(z) z_dt = -beta*z + np.sin(x) return x_dt, y_dt, z_dt #     : beta = 0.19 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 185, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Thomas, (x_0, y_0, z_0), t, args=(beta,)) 

Penarik Sistem Chaotic Bersatu Tiga Gulir (TSUCS1)

 #  : def TSUCS1(XYZ, t, alpha, beta, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*(y - x) + delta*x*z y_dt = xi*y - x*z z_dt = beta*z + x*y - epsilon*x*x return x_dt, y_dt, z_dt #     : alpha = 40 beta = 0.833 delta = 0.5 epsilon = 0.65 xi = 20 x_0, y_0, z_0 = 0.01, 0, 0 #      #  : tmax, n = 70, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(TSUCS1, (x_0, y_0, z_0), t, args=(alpha, beta, delta, epsilon, xi)) 

Penarik wang-sun

 #  : def WangSunAttractor(XYZ, t, alpha, beta, zeta, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*x + zeta*y*z y_dt = beta*x + delta*y - x*z z_dt = epsilon*z + xi*x*y return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = -0.01 zeta = 1 delta = -0.4 epsilon = -1 xi = -1 x_0, y_0, z_0 = 0.5, 0.1, 0.1 #      #  : tmax, n = 500, 30000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(WangSunAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta, epsilon, xi)) 

Kesimpulannya

Api, air, bumi, langit, matahari, bulan, bintang - semua ini adalah esensi puitis yang paling kuno. Sangat sering saya berhasil menemukan sesuatu yang sama indahnya dalam matematika. Tetapi jauh lebih sering saya bahkan tidak mengerti bagaimana membicarakan semua ini dalam bahasa matematika dan bahasa biasa. Saya tidak mengerti, tetapi saya ingin belajar.

Tetapi apa yang saya sadari 100%, adalah bahwa alat visualisasi modern memberikan kesempatan fantastis untuk mengekspresikan sikap Anda terhadap apa yang Anda lakukan sekarang, kesempatan untuk menunjukkan betapa pentingnya hal ini bagi Anda dan betapa menariknya Anda. Lakukan semuanya tanpa kata-kata.