Studi tentang neutrino menyebabkan penemuan yang tidak terduga dalam matematika

Tiga fisikawan ingin menghitung proses perubahan neutrino. Akibatnya, mereka menemukan hubungan tak terduga antara beberapa objek matematika yang paling umum.

Suatu hari di bulan Agustus, pagi hari setelah sarapan, matematikawan Terence Tao membuka email yang ditulis oleh tiga fisikawan yang tidak dikenalnya. Trinity menjelaskan kepadanya bahwa dia menemukan formula sederhana, yang, jika benar, akan menggambarkan hubungan tak terduga antara beberapa objek paling mendasar dan penting dari aljabar linier.

Rumus "terlihat terlalu bagus untuk menjadi kenyataan," kata Tao, seorang profesor di Universitas California, Los Angeles, seorang pemenang Fields , salah satu ahli matematika terkemuka di dunia. "Sesuatu yang begitu singkat dan sederhana seharusnya ada di buku teks sejak dulu," katanya. "Karena itu, pada awalnya aku berpikir - tidak, ini tidak mungkin."

Dan kemudian dia berpikir sedikit lagi.

Fisikawan - Stephen Park dari National Accelerator Laboratory. Fermi, Xining Zhang dari University of Chicago, dan Peter Denton dari Brookhaven National Laboratory - mendapat identitas matematika ini dua bulan sebelumnya, mencoba berurusan dengan perilaku aneh partikel elementer yang disebut neutrino .

Mereka memperhatikan bahwa " vektor eigen ", sulit untuk dihitung, menggambarkan dalam kasus mereka bagaimana neutrino merambat dalam materi, disamakan dengan kombinasi istilah yang dikenal sebagai "nilai eigen," yang jauh lebih mudah untuk dihitung. Selain itu, mereka menyadari bahwa hubungan antara vektor eigen dan nilai eigen - objek yang sangat umum dalam matematika, fisika, dan teknik, yang telah dipelajari sejak abad XVIII - tampaknya merupakan urutan yang lebih umum.

Meskipun fisikawan tidak dapat percaya bahwa mereka telah menemukan fakta baru yang berkaitan dengan matematika dasar seperti itu, mereka tidak dapat menemukan hubungan seperti itu baik di buku atau di artikel. Oleh karena itu, mereka memutuskan untuk mengambil kesempatan dan menghubungi Tao, meskipun faktanya ada permintaan di situsnya untuk tidak mengganggunya dalam kasus-kasus seperti itu.

"Yang mengejutkan kami, dia menjawab dua jam kemudian, dan mengatakan bahwa dia belum pernah melihat yang seperti itu sebelumnya," kata Park. Dan selain itu, dalam jawaban Tao ada tiga bukti independen identitas ini.


Xining Zhang, Peter Denton dan Stephen Park dengan formula terbuka

Satu setengah minggu kemudian, fisikawan dan Tao, yang disebut Park sebagai "selang api matematika," menerbitkan sebuah makalah di Internet yang melaporkan formula baru. Sekarang pekerjaan ini dievaluasi oleh spesialis jurnal Communications in Mathematical Physics. Dalam sebuah makalah terpisah yang diterbitkan dalam Jurnal Fisika Energi Tinggi, Denton, Park, dan Zhang menggunakan rumus ini untuk menyederhanakan persamaan yang menggambarkan perilaku neutrino.

Para ahli mengatakan bahwa rumus ini mungkin memiliki lebih banyak cara untuk diterapkan, karena dalam sejumlah besar tugas, perhitungan vektor eigen dan nilai eigen diperlukan. "Ini memiliki berbagai kegunaan," kata John Bickom , seorang spesialis dalam fisika partikel di Universitas Ohio. "Siapa yang tahu pintu apa yang bisa dia buka."

Matematikawan berpikir dengan cara yang sama. "Ini mengejutkan dan menarik," kata Van Wu , ahli matematika di Universitas Yale. "Saya tidak menduga bahwa mungkin untuk menghitung vektor eigen hanya menggunakan informasi tentang nilai eigen."

Vu dan Tao membuktikan identitas yang sama pada tahun 2009 (itulah sebabnya Denton, Park dan Zhang memutuskan untuk menghubungi Tao), namun, formula baru tidak mengikuti dengan jelas dari yang lama. Dan meskipun formula yang sama secara kebetulan muncul dalam karya matematika pada bulan Mei tahun ini, penulisnya tidak mengaitkannya dengan vektor eigen dan nilai eigen.

Dalam arti tertentu, tidak mengherankan bahwa gagasan baru tentang objek matematika yang berusia beberapa abad berasal dari fisikawan. Alam telah mengilhami penelitian matematika sejak orang mulai mengandalkan 10 jari. "Agar matematika berkembang, itu harus terhubung dengan alam," kata Vu. "Tidak ada jalan lain."

Trik Transformasi

Vektor dan nilai-nilai eigen sangat umum karena mereka mengkarakterisasi transformasi linear: operasi yang meregangkan, mengompres, memutar, atau dengan cara lain mengubah semua bagian dari objek yang sama secara sama. Transformasi ini diwakili oleh array bujursangkar angka yang disebut matriks. Satu matriks memutar objek 90 derajat; yang lain membaliknya terbalik dan membagi dua.


Menerapkan matriks ini ke objek tertentu akan mencerminkannya relatif terhadap bidang, dan juga menggandakan ketinggiannya. Vektor eigen dari matriks menggambarkan arah di mana objek tidak berubah, kecuali untuk penskalaan. Nilai-nilai eigen dari matriks menggambarkan seberapa banyak objek bersisik sepanjang vektor-vektor eigen ini.
Vektor Aigen sejajar dengan sumbu vertikal. Nilai eigennya adalah 2, karena objek tersebut menggandakan tingginya.
Eigenvektor B ada di bidang pantulan. Nilai eigennya adalah 1, karena objek tidak berubah sepanjang itu.
Eigenvector C tegak lurus terhadap bidang pantulan. Nilai eigennya adalah -1, yang berarti pantulan relatif terhadap bidang.
Dengan menghapus baris dan kolom dari sebuah matriks, matriks yang lebih kecil dapat dibuat. Nilai eigen mereka bersama dengan nilai eigen dari matriks asli dapat digunakan untuk menghitung vektor eigen dari matriks asli.

Matriks melakukan ini dengan mengubah "vektor" objek - panah matematika yang menunjuk ke setiap tempat fisik objek. Vektor eigen dari suatu matriks adalah vektor-vektor yang terus menunjuk ke arah yang sama seperti sebelumnya, setelah menerapkan matriks. Misalkan kita mengambil matriks yang memutar objek 90 derajat di sekitar sumbu x: vektor eigen diarahkan sepanjang sumbu x, karena titik-titik yang terletak pada sumbu ini tidak berputar ketika semua yang lain berputar di sekelilingnya.

Matriks yang sama dapat memutar objek di sekitar sumbu x dan kompres dua kali. Berapa banyak matriks menekan atau meregangkan vektor eigen dari objek, nilai eigen yang sesuai menggambarkan - dalam kasus ini, 1/2 (jika vektor eigen tidak berubah, nilai eigennya adalah 1).


Terence Tao

Vektor eigen dan nilai eigen independen, dan biasanya mereka harus dihitung secara terpisah, dimulai dengan baris dan kolom dari matriks itu sendiri. Siswa belajar melakukan ini untuk matriks sederhana. Tetapi formula baru berbeda dari metode yang ada. "Yang menarik tentang identitas ini adalah Anda tidak perlu tahu nilai apa pun yang terkandung dalam matriks untuk menghitung sesuatu," kata Tao.

Identitas diterapkan pada matriks Hermitian yang melakukan transformasi nyata vektor eigen (berbeda dengan angka imajiner), dan, oleh karena itu, berlaku untuk situasi yang terjadi dalam kenyataan. Rumus ini mengekspresikan setiap vektor eigen dari matriks Hermitian dalam hal nilai eigen dari matriks ini dan "matriks minor" - matriks yang lebih kecil, yang diperoleh dengan menghapus baris dan kolom dari aslinya.

Melihat ke belakang, rumus itu tampaknya masuk akal, kata Tao, karena nilai eigen dari matriks minor menyandikan informasi tersembunyi di dalam diri mereka. Namun, "misalnya, saya pribadi tidak akan pernah memikirkan hal seperti itu."

Dia mengatakan bahwa alat yang tidak terkait dengan tugas jarang muncul dalam matematika. Namun, ia percaya bahwa interkoneksi vektor eigen dan nilai eigen haruslah penting. "Sangat indah sehingga saya yakin bahwa formula akan menemukan beberapa aplikasi dalam waktu dekat," katanya. "Sejauh ini, kita hanya menggunakan satu untuknya."

Partikel serigala

Dan aplikasi ini dikaitkan dengan neutrino: yang paling aneh, paling sedikit dipelajari dan paling rahasia dari partikel fundamental yang diketahui. Setiap detik, triliunan partikel seperti itu melewati tubuh manusia, tetapi karena mereka praktis tidak menunjukkan keberadaannya, banyak dari sifatnya tetap tidak diketahui.

Menariknya, teori ini mengklaim bahwa justru perbedaan perilaku neutrino dan antineutrino yang dapat menyebabkan materi mendominasi antimateri di alam semesta . Jika dua lawan muncul dalam jumlah yang sama setelah Big Bang, mereka akan saling memusnahkan, dan tidak akan ada yang tersisa di luar angkasa kecuali cahaya. Perbedaan antara neutrino dan antineutrino dapat menimbulkan kelebihan materi yang vital. "Jika mereka berperilaku berbeda, itu akan memberi kita beberapa ide mengapa Semesta dipenuhi dengan materi," kata Deborah Harris , seorang ahli fisika di York University dan Fermilab, yang bekerja dalam eksperimen DUNE (Eksperimen Neutrino Bawah Tanah Jauh, neutrino bawah tanah yang dalam Percobaan) yang dirancang untuk mengukur perbedaan tersebut.

Percobaan, yang akan mengukur karakteristik neutrino diluncurkan dari Fermilab di Illinois ke detektor bawah tanah yang terletak 1.300 km dari sumber di South Dakota, menggunakan fakta bahwa ada tiga jenis neutrino yang berbeda - elektron, muon, dan tau. Namun, masing-masing jenis adalah campuran mekanis-kuantum, dan neutrino berosilasi, mengubah jenisnya saat bepergian. Saat neutrino berjalan dari Fermilab, campurannya berubah, sehingga muon neutrino dapat berubah menjadi elektron atau tau neutrino.

Osilasi ini dijelaskan oleh matriks 3x3 yang sangat kompleks. Berdasarkan vektor eigen dan nilai eigen, fisikawan dapat menghitung ekspresi yang menggambarkan probabilitas bahwa neutrino muon akan berubah menjadi neutrino elektronik pada saat tiba di South Dakota. Mereka juga menghitung kemungkinan bahwa muon neutrino akan menjadi elektron antineutrino.


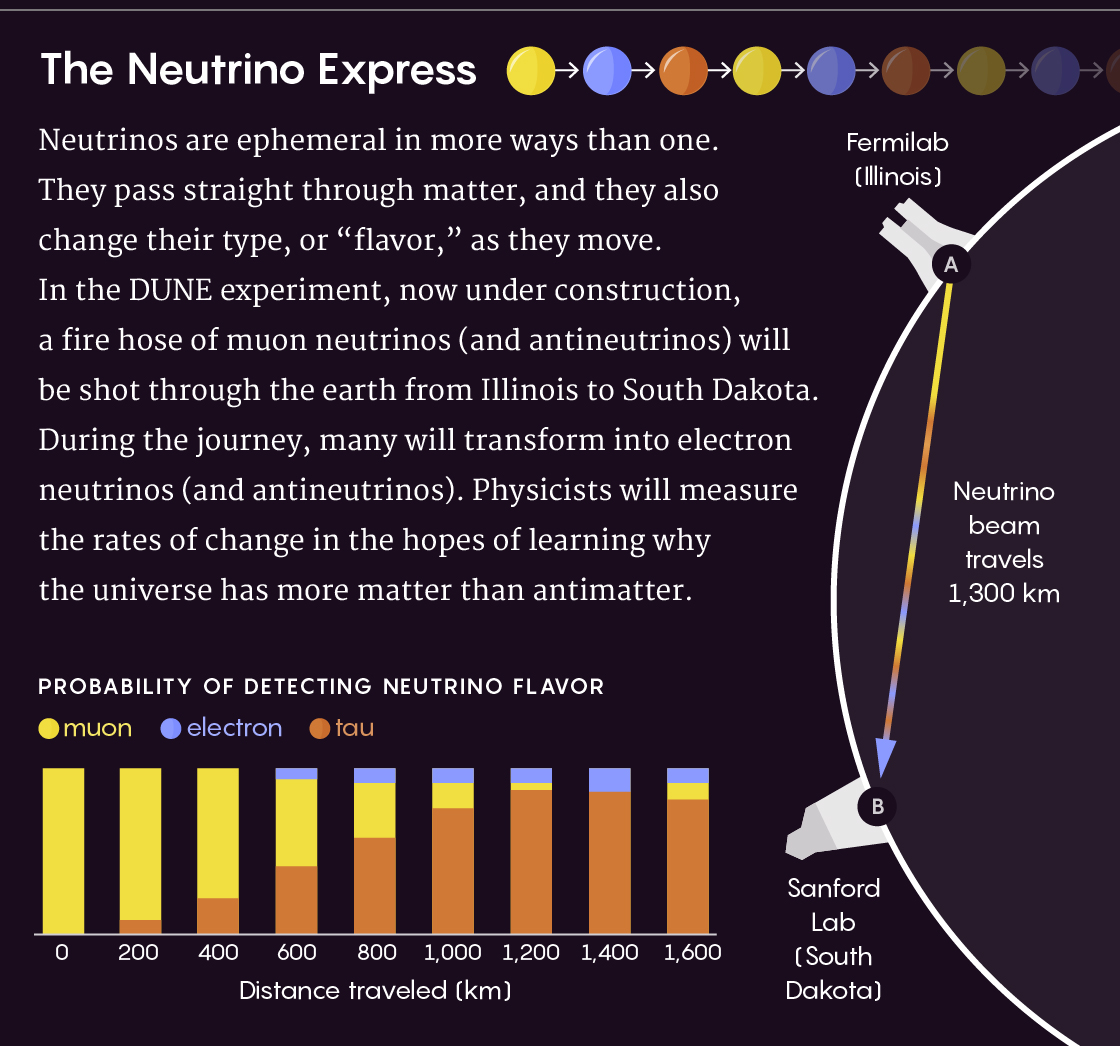Partikel fana dari neutrino tidak hanya melewati materi, tetapi juga mengubah tipenya dengan cepat. Dalam percobaan DUNE, sinar neutrino akan diluncurkan, banyak di antaranya akan mengubah tipenya dalam perjalanan dari sumber ke target. Perubahan ini akan diukur oleh fisikawan.
Diagram menunjukkan kemungkinan mendeteksi neutrino dari berbagai jenis tergantung pada jarak perjalanan mereka dalam km. Kuning - muon, biru - elektronik, coklat - tau.

Ungkapan-ungkapan ini mengandung yang tidak diketahui: "fase pelanggaran invarian CP ", yang menunjukkan bagaimana hukum osilasi neutrino dan antineutrino berbeda satu sama lain. Dengan mengukur dan membandingkan rasio osilasi nyata, para ilmuwan dengan DUNE dapat menghitung hal yang tidak diketahui ini. Jika fase gangguan cukup besar, ini akan membantu menjelaskan mengapa alam semesta dipenuhi dengan materi.

Dan seolah-olah kesulitan ini tidak cukup, satu efek aneh, prasyarat yang pertama kali ditemukan pada 1978 oleh fisikawan Lincoln Wolfenstein, membuat matriks neutrino semakin kompleks. Neutrino jarang berinteraksi dengan materi dalam pengertian yang biasa, tetapi Wolfenstein menemukan bahwa perjalanan mereka melalui materi, tidak seperti ruang kosong, masih mengubah cara mereka menyebar. Kadang-kadang neutrino yang menembus materi berinteraksi dengan elektron dalam atom, pada dasarnya mengubah tempat dengannya: neutrino elektron berubah menjadi elektron dan sebaliknya.

Pergantian tersebut memperkenalkan istilah baru ke dalam matriks, yang mempengaruhi neutrino elektron, yang sangat menyulitkan matematika. Ini adalah efek dari Mikheev - Smirnov - Wolfenstein [yang diprediksi dan diselidiki secara teoritis oleh fisikawan Soviet Stanislav Mikheev dan Alexey Smirnov pada tahun 1985 berdasarkan kasus osilasi neutrino dalam media dengan kepadatan konstan dipertimbangkan dalam Wolfenstein] mendorong Park, Zhang, dan Denton untuk menemukan cara menyederhanakan perhitungan. .

Ekspresi untuk menghitung nilai eigen lebih sederhana daripada ekspresi untuk vektor eigen, jadi Park, Zhang dan Denton menggunakan ini sebagai titik awal. Sebelum ini, mereka mengembangkan metode baru untuk perkiraan perhitungan nilai eigen. Berdasarkan hal itu, mereka memperhatikan bahwa ekspresi panjang untuk vektor eigen dari karya sebelumnya sama dengan kombinasi nilai eigen ini. Menyatukan semuanya, "Anda dapat dengan mudah dan cepat menghitung osilasi neutrino dalam materi," kata Zhang.

Mengenai bagaimana mereka melihat pola dari mana formula ini mengikuti, fisikawan tidak sepenuhnya yakin. Park mengatakan bahwa mereka hanya memperhatikan manifestasi individual dari pola dan menggeneralisasikannya. Dia juga mengakui bahwa dia pandai memecahkan teka-teki. Dia adalah penulis bersama dari keteraturan penting lainnya, ditemukan pada tahun 1986, yang memfasilitasi perhitungan di bidang fisika partikel, dan juga hingga hari ini menginspirasi para ilmuwan untuk penemuan baru.

Namun, fakta bahwa perilaku aneh neutrino dapat menyebabkan munculnya ide-ide baru terkait dengan matriks mengejutkan banyak orang. "Orang-orang telah memecahkan aljabar linear untuk waktu yang sangat, sangat lama," kata Park. "Saya masih menunggu seseorang mengirimi saya email yang isinya: Jika Anda melihat karya Cauchy yang sedikit diketahui ini, maka ada formula ini dalam catatan ke lampiran ketiga."

Perbedaan kecil

Sebenarnya, formula yang sama sudah diketahui, tetapi tidak ada yang menyadarinya, karena itu bertopeng.

Pada bulan September, Tao menerima email lain yang tidak terduga, kali ini dari Jiyuan Zhang, seorang mahasiswa pascasarjana bidang matematika dari University of Melbourne di Australia. Zhang menunjuk keberadaan formula yang setara dalam sebuah karya yang ditulisnya dengan kuratornya Peter Forester pada bulan Mei, sebelum karya Tao dan tiga fisikawan muncul. Zhang dan Forrester bekerja di bidang matematika murni, teori matriks acak. Mereka menerapkan formula ini, mengeksplorasi masalah yang terkait dengan solusi Tao dan rekan-rekannya pada tahun 1999.

Forester menjelaskan kepada kami bahwa untuk pertama kalinya formula ini muncul dalam bentuk lain dalam karya 2001, yang ditulis oleh Julia Baryshnikova , seorang ahli matematika yang sekarang bekerja di University of Illinois di Urbana-Champaign, yang menjadi dasar karya Forester dan Zhang. Tetapi para ahli matematika ini mendeskripsikan objek-objek identitas mereka bukan sebagai vektor eigen, tetapi sebagai istilah yang diperlukan untuk menghitung nilai-nilai eigen dari matriks-matriks minor tertentu yang muncul dalam proses penyelesaian masalah mereka.

Forester menyebut formula dalam karyanya dengan Zhang "identik" dengan yang digunakan oleh Tao dan tiga fisikawan. Tao menyebut formula itu "hampir identik," merujuk satu sama lain dengan cara yang sama seperti dua sisi ilusi kelinci / bebek. "Beberapa orang mencari kelinci, yang lain hanya mencari bebek," katanya.



Denton menulis dalam email bahwa formula yang ada sebelumnya "dekat dengan hasil kami, tetapi tidak sempurna." Dia menambahkan bahwa "mengingat pentingnya vektor eigen untuk banyak masalah, kami masih berpikir bahwa hasil kami sangat berbeda dari yang lain untuk menganggapnya baru."

Mungkin tidak begitu aneh bahwa di daerah ini dalam satu musim panas setelah beberapa abad, kegembiraan yang tiba-tiba dapat muncul. "Ada banyak contoh penemuan simultan dalam matematika," kata Tao. - Hasilnya entah bagaimana menggantung di udara. Dan orang-orang mulai mencari mereka di tempat yang tepat. "