Pengakuan sirkuit digital. Elemen-C yang digeneralisasi

Alexander Kushnerov
12/18/2019

Bahkan seorang insinyur yang berpengalaman kadang-kadang dapat menemukan kesulitan untuk rute sirkuit sehingga trek (atau kabel) tidak mengganggu operasi yang semestinya. Dalam pendekatan pertama, tata letak dan jumlah node, yang kabel terhubung ke setiap node dan panjang kabel setelah bercabang, mempengaruhi kualitas kabel. Jika kita menganggap panjang kabel sebagai penundaan, maka operasi yang benar dari sirkuit digital asinkron mungkin tidak bergantung pada penundaan di beberapa kabel. Di masa depan, kita akan menyebut kabel semacam itu aman, dan percabangan kabel semacam itu - benar-benar aman (FGP). Pada artikel ini, kami akan menunjukkan bagaimana rangkaian universal dua belas transistor dapat membuat beberapa cabang sepenuhnya aman.

Pertimbangkan skema “kupu-kupu” [1], [2] yang ditunjukkan pada Gambar. 1. Rangkaian ini menghasilkan pulsa p dan q yang terpisah, yang dapat digunakan untuk mengontrol transistor daya. Buffer pada Gbr. 1 menunjukkan kabel yang aman. Penundaan semua kabel lainnya diasumsikan nol. Jeda antara pulsa diatur oleh penundaan buffer dengan wz. Di masa mendatang, kami tidak akan menggunakan buffer untuk menunjukkan keterlambatan elemen. Kabel dan cabang di semua sirkuit artikel ini diuji untuk keselamatan (output persistensi) di Workcraft [3]. Grafik transisi sinyal (STG) diperoleh dari sirkuit dengan menyelesaikan konflik CSC. Ilustrasi menunjukkan STG disederhanakan di mana sinyal buffer dihapus. Timing diagram (TD) pada Gambar. 1 dibangun sesuai dengan STG yang sesuai.


Fig. 1. Sirkuit "kupu-kupu", STG dan TD-nya dengan asumsi bahwa keterlambatan kabel adalah nol.

Dari teori [1], [2] diketahui bahwa rangkaian pemicu RS sensitif terhadap keterlambatan kabel dalam cross-coupling. Itulah sebabnya buffer dalam cross-link di Fig. 1 hilang. Dengan demikian, dua elemen pemicu harus berada pada jarak minimum satu sama lain. Jika ini sulit dilakukan, maka dua elemen dapat diganti dengan satu elemen kompleks dengan umpan balik. Misalnya, elemen x dan xb di sirkuit kupu-kupu dapat diganti seperti yang ditunjukkan pada Gambar. 2. Selain itu, kami mendapatkan FGP pada output elemen kompleks.


Fig. 2. Varian dari sirkuit pada Gambar. 1 dan STG-nya dengan asumsi bahwa keterlambatan kabel adalah nol.

Implementasi skema pada Gambar. 1 dan Gbr. 2 membutuhkan masing-masing 16 dan 20 transistor. Selain itu, diagram pada Gambar. 2 lebih lambat, karena inverter wb1, wb2 dan inverter di dalam elemen 2 OR-AND harus beralih dua kali per siklus. Performa lambat biasanya adalah harga FGP. Namun, ada pengecualian untuk aturan ini. Misalnya, dalam Gbr. 3 menunjukkan skema pemicu penghitungan asinkron (AST) [4] yang memiliki dua FGP.


Fig. 3. AST dan STG-nya dengan asumsi bahwa keterlambatan kabel adalah nol.

Kerugian dari sirkuit pada Gambar. 3 adalah sejumlah besar kabel dan fakta bahwa sebagian besar dari mereka berpotongan. Ini dapat memperumit tata letak, terutama jika jumlah lapisan dengan trek terbatas atau ditempati oleh senyawa lain. Jadi, Anda perlu mencari beberapa kompromi antara jumlah kabel, jumlah transistor dan jumlah FGP. Contoh skema kompromi semacam itu dengan satu FGP adalah AST yang ditunjukkan pada Gambar. 4. Ini adalah modifikasi kecil dari rangkaian dari [5]. Perhatikan bahwa di sini, seperti pada diagram pada Gambar. 2, basis campuran digunakan. Untuk mengimplementasikan AST ini tanpa indikator (XOR pada wi2, wi4 dan g5), diperlukan 26 transistor. Ini hanya dua transistor lebih dari AST pada Gambar. 3.


Fig. 4. Kompromikan AST dan STG-nya, ketika penundaan kabel adalah nol.

Perhatikan bahwa semua elemen dengan umpan balik pada Gambar. 2 dan Fig. 4 adalah kasus khusus dari elemen-C umum (gC). Itu diberikan sebagai [6]: $$$y = S (x) + y \ overline {R} (x)$ dimana $$$S (x)$ dan $$$R (x)$ Apakah fungsi pemasangan dan reset memenuhi kondisi tersebut $$$S (x) R (x) = 0$ . Kasus khusus dari elemen gC juga merupakan elemen NCL, yang digunakan dalam skema untuk pemrosesan data. Perhatikan bahwa elemen NCL terbesar memiliki empat input dan diimplementasikan pada 28 transistor [7]. Hal ini dapat dijelaskan oleh fakta bahwa dengan jumlah transistor yang lebih besar, kabel menjadi relatif panjang dan penundaan di dalamnya mulai mempengaruhi operasi elemen.

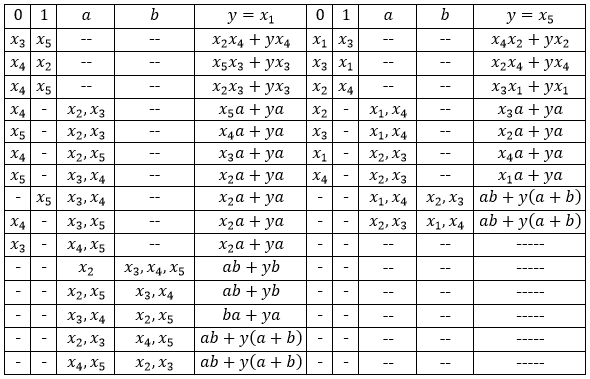
Pertimbangkan rangkaian transistor yang ditunjukkan pada Gambar. 5. Ini mengimplementasikan fungsi lima variabel [8], [9] $$$f (x) = x_1 x_3 + x_2 x_4 + x_5 (x_1 x_4 + x_2 x_3)$ . Tabel 1 menunjukkan fungsi SDNF dan SKNF $$$f (x)$ dan fungsi rangkapnya $$$φ (x) = \ overline {f (\ overline x)}$ . Dari tabel ini jelas bahwa dengan bertukar $$$x_2$ dan $$$x_3$ masuk $$$f (x)$ kita dapatkan $$$φ (x)$ dan sebaliknya. Dalam kasus $$$x_2 = x_3 = y$ , kami mendapatkan fungsi self-dual $$$f (x, y) = \ overline {f (\ overline x, \ overline y)} = x_1 x_4 x_5 + y (x_1 + x_4 + x_5)$ .


Fig. 5. Skema yang mengimplementasikan fungsi lima variabel.

Tabel 1. Bentuk fungsi logis untuk rangkaian pada Gambar. 5.


Catat itu $$$x_2 = x_3 = y$ berarti bahwa empat transistor yang sesuai harus diaktifkan secara bersamaan. Bahkan jika kabel setelah bercabang y memiliki penundaan yang sama, ini tidak cukup, karena momen switching dari transistor ditentukan oleh tegangan di gerbangnya. Dari sudut pandang ini, analisis rangkaian pada Gambar. 5 dibuat di [10]. Namun, analisis ini tidak lengkap, karena hanya implementasi elemen C dua input yang dipertimbangkan. Untuk melakukan analisis penuh, Anda harus terlebih dahulu menemukan semua opsi untuk menggabungkan input, atau, lebih formal, semua fungsi dari sejumlah kecil variabel yang dapat diperoleh dari $$$f (x)$ . Pencarian semacam itu dilakukan dalam bentuk yang agak disederhanakan, dan hasilnya ditampilkan di lampiran. Sebagian besar fitur ditemukan dalam beberapa variasi. Dari mereka perlu untuk memilih orang-orang yang memberikan skema yang bebas dari kompetisi [11]. Semua fungsi yang diperoleh, jumlah varian masing-masing dan jumlah tabel yang sesuai dalam lampiran diberikan dalam tabel 2. Angka-angka dengan tanda bintang menunjukkan fungsi ganda.

Tabel 2. Elemen gC diimplementasikan oleh sirkuit pada Gambar. 5.


Fungsi 2 dan 2 *, 5 dan 5 *, 7 dan 7 * bersifat ganda, dan fungsi 4 dapat diperoleh dari fungsi 4 * dengan menukar a dan c. Perhatikan bahwa selain fungsi 6 *, semua fungsi lainnya adalah ambang. Ini bisa dijelaskan oleh fakta bahwa $$$f (x)$ adalah isotonik (unate positif) dan fakta bahwa untuk empat atau kurang variabel fungsi isotonik bertepatan dengan pseudo-threshold [12]. Pertanyaan tentang opsi apa untuk fungsi 1 *, 3 * dan 6 * dalam artikel ini tetap terbuka.

Pertimbangkan kasus fungsi 2 dan 2 * sebagai contoh. Sesuai dengan salah satu opsi (tabel P3 dalam lampiran) $$$x_1 = x_4 = a$ dan $$$x_2 = x_3 = b$ . Biarkan jalan keluar $$$y$ terputus dari pintu masuk $$$x_5$ dan biarkan sinyal dihapus dari input inverter. Ini memungkinkan Anda membangun distributor konveyor sel [13] yang ditunjukkan pada Gambar. 6. Elemen-elemen dalam sel ini berbeda, tetapi karena fakta bahwa input digabungkan, mereka berdua menerapkan fungsi self-dual yang sama. Perhatikan bahwa elemen cross-linked di sirkuit pada Gambar. 1, dalam Gbr. 3 dan Gambar. 6 adalah kasus khusus dari konstruksi dasar untuk implementasi yang sempurna [2]. Jadi, harus ada aturan untuk mengubah sirkuit desain dasar menjadi sirkuit elemen gC dan sebaliknya.


Fig. 6. Distributor konveyor sel.

Dari sudut pandang teknologi, transistor harus “dirangkai” ke bus polisilikon. Seperti implementasi sirkuit pada Gambar. 5 diberikan dalam [14]. Untuk mengatur keadaan awal, transistor p-MOS dan n-MOS dapat digunakan, yang menciptakan pembagi tegangan dengan transistor di inverter. Imunitas kebisingan dari sirkuit dapat ditingkatkan dengan bantuan transformasi STG tertentu [15].

Ucapan Terima Kasih

Penulis sangat berterima kasih kepada Svetlana Frolova (OmSU) karena memindai artikel [1], dan juga kepada Sergey Bystrov untuk inspirasi.

Aplikasi

MuPAD digunakan untuk mendapatkan hasil yang disajikan dalam bagian ini. Biarkan output y terhubung hanya ke salah satu input. Tabel A1 menunjukkan bahwa dalam hal ini $$$S (x) R (x) ≠ 0$ . Untuk mendapatkan fungsi yang mana $$$S (x) R (x) = 0$ , Anda bisa menggabungkan beberapa variabel atau menetapkan konstanta padanya. Fungsi untuk kasus menggabungkan dua variabel diberikan pada tabel A2. Opsi lain tidak memberi $$$S (x) R (x) = 0$ . Karena empat fungsi pertama pada Tabel A1 bertepatan hingga permutasi variabel, kami hanya akan mempertimbangkan yang pertama dan kelima. Kasing $$$y = y (∀)$ dan $$$y = (∀) + y$ tidak menarik, karena pada awalnya kita hanya dapat mengatur ulang elemen gC, tetapi kita tidak dapat menginstalnya, dan pada yang kedua - sebaliknya. Manipulasi dengan variabel memungkinkan untuk memperoleh dari tabel P1 fungsi empat dan tiga variabel, yang masing-masing diberikan dalam tabel P3 dan tabel P4.

Tabel A1. Fungsi lima variabel.


Tabel A2. Fungsi empat variabel.


Tabel P3. Fungsi empat variabel diperoleh dari Tabel A1.


Tabel A4. Fungsi ketiga variabel tersebut diperoleh dari Tabel A1.

Sastra

[1] V. I. Varshavsky, M. A. Kishinev, A. R. Taubin dan B. S. Zirlin, “Analisis sirkuit logika asinkron. II Jangkauan status pengoperasian dan efek keterlambatan kabel, ”Izv. Akademi Ilmu Pengetahuan Uni Soviet. Sibernetika Teknis, no. 4, hlm. 84-97, 1982.
[2] Varshavsky, V. I. (ed.), Kontrol otomatis proses asinkron dalam komputer dan sistem diskrit, Nauka, 1986.
[3] workcraft.org .
[4] RC Todd, “Sistem logika”. Paten US3609569, 28 Sep. 1971.
[5] EA Vittoz, "Struktur logika pembagian frekuensi". Paten US3829714, 13 Agustus 1974.
[6] J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno dan A. Yakovlev, sintesis Logika untuk pengontrol dan antarmuka asinkron, Springer, 2002.
[7] A. Kondratyev, “Aliran multi-rel asinkron dengan deteksi penyelesaian dan sistem serta metode untuk mendesain yang sama.” Paten US6526542, 25 Feb. 2003
[8] JJ Gibson, "Sirkuit logika yang menggunakan transistor efek medan." Paten US3439185, 15 Apr. 1969.
[9] R. Miller, Teori switching circuit. Volume I. Skema kombinasi, Sains, 1970.
[10] K. van Berkel, “Waspadalah dengan garpu isochronic,” Integrasi, vol. 13, tidak. 2, hlm. 103-128, 1992.
[11] P. Kudva, G. Gopalakrishnan, H. Jacobson dan SM Nowick, "Sintesis jaringan gerbang kompleks CMOS yang dapat disesuaikan bebas bahaya di bawah perubahan multi-input," dalam Design Automation Conf., 1996.
[12] GW Fagerlin, Enumerasi fungsi pseudo-separable dari lima variabel. M.Sc. tesis, Universitas Illinois, 1968.
[13] V. I. Varshavsky, A. Yu, Kondratiev, N. M. Kravchenko, dan B. S. Tsirlin, “Distributor Asinkron”. Paten SU1598142, 07/10 1990.
[14] SW Cheng, “Sirkuit logika CMOS pohon-H,” di IEEE Conf. tentang Elektronik, Sirkuit dan Sistem, 2008.
[15] A. Taubin, A. Kondratyev, J. Cortadella dan L. Lavagno, "Transformasi perilaku untuk meningkatkan kekebalan kebisingan dalam spesifikasi asinkron," dalam IEEE Symp. di Async. Sirkuit dan Sistem, 1999.