Mungkin sulit untuk menyebut kubah geodesik sesuatu yang tidak biasa atau baru. Dalam artikel ini, saya akan berbicara sedikit tentang desain ini secara umum, tentang strukturnya, dan juga menunjukkan, sebagai contoh, bagaimana saya mempertimbangkan sesuatu tentang topik ini. Kode juga akan.
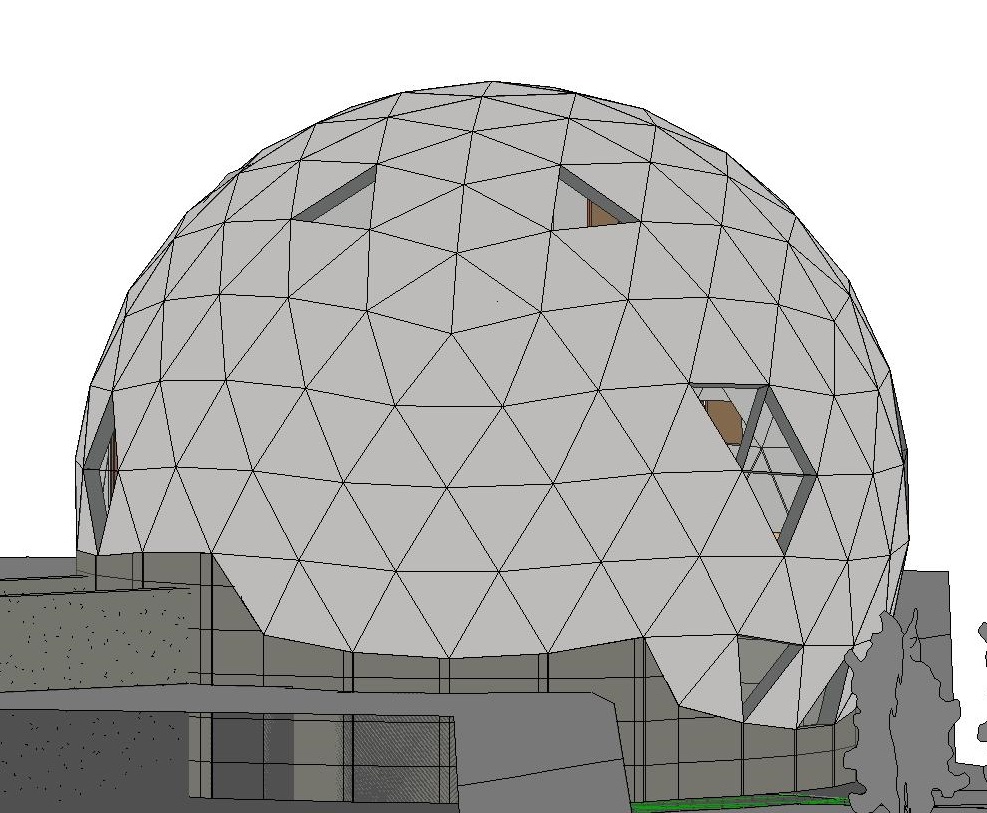
Saya tidak akan mengutip Wikipedia. Mengapa saya memilih kubah sebagai rumah saya?
- Dengan volume yang sama, luas permukaan bola akan kurang dari bentuk lainnya. Ini secara positif mempengaruhi konsumsi material dan konsumsi energi selama operasi.
- Saya suka seperti apa bola itu.
- Ini adalah proyek rekayasa yang menarik, dalam arti tertentu, bahkan sebuah tantangan. Itu sulit, sulit dan karenanya menyenangkan!
Bagaimana bola geodesik ini diatur secara umum? Pada pandangan pertama, sepertinya ini adalah semacam jalinan tepi dan sulit untuk menangkap sistem. Kami akan mencoba memecahkannya.
Dasar dari struktur tersebut adalah icosahedron atau octahedron. Secara umum, polihedron biasa.
Dalam kasus saya, justru icosahedron dan digunakan lebih sering. Selanjutnya, kita mengambil satu wajah dan menggantinya dengan beberapa segitiga yang simpulnya terletak pada bola yang pusatnya bertepatan dengan pusat icosahedron. Kedengarannya tidak terlalu bagus. Mari kita ngelantur.
Ada kalkulator
www.acidome.ru yang luar
biasa yang memungkinkan Anda untuk memutar surveyor secara real time. Ambil icosahedron sebagai pangkalan, atur frekuensinya menjadi 1, bagian dari bola 1/1.

Ini adalah icosahedron utama kami. Frekuensi adalah berapa banyak bagian yang akan kita pecahkan setiap tepi icosahedron. Kami menetapkan 3.4, 5 dan tidak ada yang menjadi jelas. Beralih ke mode atap dan cari pentagon. Di tempat-tempat di mana kita memiliki puncak icosahedron - akan ada pentagon. Antara tiga pentagon adalah wajah icosahedron.

Jika Anda hati-hati melihat geodesik dan tahu apa yang harus dicari (biasanya segi lima), maka keteraturan struktur menjadi terlihat. Di Biosphere di Montreal, dengan uji tuntas, Anda dapat menemukan segilima dan menghitung frekuensinya. Frekuensi kami sama dengan jumlah tepi antara dua pentagon.
"Besar" segitiga sendiri, dengan simpul di bagian atas icosahedron, juga memiliki struktur. Pada atap asam, ini terlihat dalam warna. Segitiga terletak secara simetris sehubungan dengan pusat segitiga "besar". Jumlah tipenya kurang dari jumlah total segitiga. Dalam kasus frekuensi 5 segitiga unik 9.

Dalam proses mendesain rumah, saya dihadapkan dengan tugas membangun bola di Dynamo. Ini adalah alat yang memungkinkan Anda mengajarkan Autodesk Revit untuk bekerja dengan formulir yang kompleks. Lingkungan pemrograman visual yang demikian.
Googling, saya bahkan menemukan sketsa yang membuat bola geodesik di Dynamo. Dia membangun bola, tetapi bukan yang itu.
Ini masalahnya. Ketika kita mengambil satu sisi icosahedron dan membaginya menjadi segitiga kecil - ini bisa dilakukan dengan beberapa cara. Dalam acidome, saklar "metode pemisahan" bertanggung jawab untuk ini.
Sketsa yang ditemukan membuat bola menggunakan metode akor yang sama. Apa artinya ini? Kami mengambil segitiga besar icosahedron, membagi masing-masing ujungnya menjadi jumlah bagian yang kami butuhkan, menghubungkan titik-titik di tepi satu sama lain dan mendapatkan kotak datar segitiga. Lalu kami memproyeksikan kisi ini ke bola. Semuanya akan baik-baik saja, tetapi ukuran segitiga ini sendiri sangat berbeda. Yang paling utama. Dapat dimengerti, pusat dari segitiga "besar" berada pada jarak maksimum dari bola. Ini buruk, karena dalam hal ini lebih sulit untuk mengoptimalkan konsumsi bahan. Akan ada lebih banyak limbah.
Metode pemisahan lainnya (dengan busur yang sama) mengasumsikan bahwa kita membangun di atas segitiga "besar" dari busur dan sudah membaginya menjadi bagian yang sama. Pendekatannya berbeda, proyeksi sederhana tidak bisa dilakukan.
Sketsa itu tidak cocok. Saya mencoba memperbaikinya dan pada akhirnya saya harus terjun ke bisnis ini dengan kepala.
Ternyata, di samping lingkungan visual, Dynamo memiliki built-in Python. Saya belum pernah melihat bahasa ini sebelumnya, tetapi di mana bahasa kita tidak hilang? Pada akhirnya, itu hanya alat.
Maka akan ada potongan kode, harap perhatikan bahwa ini adalah hello world saya dengan python, dan tujuannya bukan untuk membangun solusi yang paling efektif dan efisien, tetapi untuk membangun bola yang tepat.
Metode busur sama.
Kami mengambil salah satu wajah icosahedron dan membangun busur dari sudut segitiga ini.
for k, edge in enumerate(curves):

Kemudian kami membagi busur menjadi bagian yang sama dan menghubungkan titik pada busur dengan busur baru. Semua busur memiliki satu pusat - pusat bola. Poin terhubung tidak semua dengan semua, tetapi dengan nama yang sama. Dalam gambar itu terlihat lebih sederhana daripada dalam kode.
for edge_index, point_list in enumerate(points): edge_arcs = [] for point_index, point in enumerate(point_list): next_edge_index = edge_index + 1 if len(points) == next_edge_index: next_edge_index = 0 end_point_index = n - point_index - 2 arc = Arc.ByCenterPointStartPointEndPoint(center_point, points[next_edge_index][end_point_index], point) if arc.SweepAngle > 90: arc = Arc.ByCenterPointStartPointEndPoint(center_point, point, points[next_edge_index][end_point_index]) arc_points_count = n - point_index - 1; pp = Arc.PointsAtEqualSegmentLength(arc, arc_points_count) for po in pp: on_arc_points.append(po) edge_arcs.append(arc) edges_arcs.append(edge_arcs)

Ups, dan busur tidak berpotongan! Googling yang tidak terlalu lancar membawa saya ke sebuah buku yang menegaskan asumsi saya bahwa perlu menggunakan pusat segitiga yang dibentuk oleh persimpangan busur sebagai bagian atas tepi geodesik. Saya juga merokok sumber asam, tetapi saya tidak ingat jika saya menemukan konfirmasi di sana. Saya ingat itu menarik.
Pusat-pusat entah bagaimana harus ditemukan. Ini adalah pusat dari segitiga dan itu tidak sulit, tetapi perlu untuk memahami di mana segitiga ini berada di tumpukan poin. Menurut saya, opsi termudah untuk menghubungkan titik-titik yang paling dekat satu sama lain.
for point in on_arc_points: distance = []

Sekarang kita perlu menghubungkan titik-titik yang dikumpulkan pada tahap yang berbeda, yang merupakan simpul dari tepi bola geodesik. Dalam gambar, titik-titik ini terlihat jelas, tetapi ketika mereka berada dalam array - semuanya lebih rumit. Ada beberapa opsi, tetapi karena tugasnya adalah mendapatkan skrip yang berfungsi dengan sedikit usaha, ini keluar:
Segmen siap. Mungkin ada semacam cara yang tepat untuk menyelesaikan masalah ini, tetapi saya membuka sendiri.

Kemudian segmen dibuka, disalin beberapa kali, disalin, dan bola lengkap diperoleh. Berikut adalah salah satu tikungan:
v = Vector.ByTwoPoints(sphere_center, curves[0].StartPoint) for face_triangle in face_triangles: geodesic_sphere.append(Geometry.Rotate(face_triangle, sphere_center, v, 72))
Script keluar jelek, saya menyalinnya beberapa kali, karena ada masalah dengan mengekspor ke Revit. Pikir ada masalah dengan konstruksi. Akibatnya, di forum Dynamo, orang India meminta orang Ukraina dan semuanya berhasil!
Sekarang Anda dapat membangun bola frekuensi dan diameter apa pun. Perbandingan ukuran dengan hasil asam menunjukkan bahwa semuanya menyatu dengan akurasi tinggi. Pengulangan itu bagus.

Saya juga mulai mengoptimalkan ukuran untuk meminimalkan panen. Karena semua ukuran ada di tangan saya, itu tidak begitu sulit. Hasilnya, jari-jari bola berubah menjadi 5,65 meter pada frekuensi 5. Dimensi tersebut memungkinkan saya untuk menggunakan bahan dengan lebar 125 cm dengan cukup efektif.Lebar tersebut adalah lembaran OSB, lembaran logam, isolasi, drywall. Dengan optimalisasi yang baik, jumlah kliping minimal. Hasil terbaik dapat dicapai dengan menghitung tata letak segitiga pada materi, tetapi saya tidak melakukan ini.
Lebih lanjut itu lebih mudah, karena Revit memakan bentuk yang rumit dan memungkinkan bekerja dengannya dengan keberhasilan yang hampir sama dengan paralel-persegi.
Tentu saja, kesulitan tidak berakhir di sana, tetapi ini adalah kisah yang sama sekali berbeda.