Wawancara dengan Will Kurt tentang buku barunya, Bayesian Statistics - It's Great

Halo, Habr!

Pada akhir tahun, kami dapat berbagi dengan Anda berita bahwa kami mulai mengerjakan Bayesian Statistics the Fun Way oleh No Starch Press. Kami menawarkan terjemahan wawancara terperinci dengan penulis buku; teks tersebut menyangkut buku itu sendiri dan topik terkait, dan bahkan bacaan tambahan.




Saya, seperti kebanyakan pengembang, langsung tertarik pada banyak hal: pemrograman fungsional, sistem operasi, sistem tipe, sistem terdistribusi dan ilmu data. Itu sebabnya saya sangat terinspirasi untuk mengetahui bahwa Will Kurt , penulis Get Programming with Haskell , menulis sebuah buku tentang statistik Bayesian dari No Starch Press. Tidak banyak orang menulis buku tentang berbagai topik. Saya yakin Will memiliki sesuatu untuk dibagikan kepada pembaca di buku barunya - dan tidak kecewa karenanya. Buku ini adalah bahan pengantar yang sangat baik, terutama bagi mereka yang tidak terlalu pandai matematika, tetapi masih ingin mencapai sesuatu di bidang Ilmu Data. Saya merekomendasikan membaca buku baru Kurt setelah Think Stats, tetapi sebelum Pemrograman Python Probabilistik: Bayesian Inference and Algorithms, Bayesian Analysis with Python dan Doing Bayesian Data Analysis.

1. Mengapa kita perlu buku lain tentang statistik?

Hampir semua dari banyak buku yang ada saat ini tentang statistik Bayesian menunjukkan bahwa pembaca sudah memiliki gagasan umum tentang statistik dan dasar yang kuat dalam pemrograman. Oleh karena itu, saat ini, statistik Bayesian sering dianggap sebagai alternatif lanjutan untuk statistik klasik (yaitu frekuensi). Dengan demikian, meskipun statistik Bayes semakin populer, materi di dalamnya dirancang terutama untuk orang-orang yang sudah memiliki pelatihan kuantitatif yang baik.

Ketika seseorang memutuskan untuk sekadar "mempelajari statistik", ia mengambil sebuah buku pengantar di mana statistik disajikan dari sudut pandang frekuensi, membacanya, telah setengah menemukan banyak tes dan aturan, dan merasa bahwa seluruh topik ini sangat membingungkan. Saya ingin menulis buku tentang statistik Bayesian sehingga siapa pun dapat mengambil, membaca dan, setelah membaca, mendapatkan ide intuitif tentang apa yang harus dipikirkan secara statistik dan bagaimana menyelesaikan masalah nyata dengan bantuan statistik. Saya tidak melihat alasan mengapa statistik Bayesian tidak dapat berfungsi sebagai kursus pengantar pertama dalam topik ini untuk pemula absolut.

Saya akan sangat senang jika suatu hari nanti dengan kata "statistik" orang mulai berarti statistik Bayesian, dan statistik frekuensi menjadi hanya salah satu ceruk akademis. Untuk ini, lebih banyak buku diperlukan di mana kenalan dengan statistik untuk kalangan luas pembaca akan diusulkan menggunakan metode Bayesian, apalagi, penulis memperhitungkan bahwa ini mungkin kenalan pertama pembaca dengan statistik.
Saya segera berpikir untuk menyebut buku ini "Statistics the Fun Way", tetapi saya berpikir bahwa saya mungkin akan mendapatkan banyak surat kemarahan dari orang-orang yang membeli buku seperti itu untuk mempersiapkan ujian masuk untuk statistik - dan menemukan itu benar-benar berbeda di sana! Saya berharap buku saya akan menjadi langkah kecil menuju waktu ketika statistik Bayesian akan diminta pada ujian masuk, dan akan disarankan untuk membaca buku seperti itu bahkan bagi mereka yang baru saja mempersiapkan ujian.

2. Apa target audiens buku ini? Bisakah seseorang membacanya tanpa latar belakang matematika?

Bekerja pada "statistik Bayesian hebat", saya mencoba membuat sebuah buku, pada prinsipnya, dapat dipahami oleh siapa saja yang belajar matematika dalam lingkup program untuk sekolah menengah. Bahkan jika Anda hanya samar-samar mengingat aljabar, laju presentasi dalam sebuah buku sedemikian rupa sehingga Anda bisa mengikutinya. Statistik Bayesian memerlukan analisis matematika yang sangat sedikit dan semua lebih disederhanakan dengan sedikit dukungan kode perangkat lunak, jadi saya menambahkan dua aplikasi ke buku yang memberikan dasar-dasar bahasa R. Bahan ini cukup bagi R untuk melayani Anda sebagai kalkulator canggih, dan gagasan dasar analisis matematika disajikan dalam sedemikian rupa sehingga Anda bisa mengetahui semua contoh dari buku ini, di mana datang ke integral. Namun, saya berjanji bahwa untuk membaca buku ini Anda tidak perlu menyelesaikan masalah dari bidang analisis matematika.

Selain itu, sebanyak saya bekerja keras, berusaha meminimalkan jumlah pengetahuan matematika yang diperlukan untuk membaca buku, saat Anda membacanya, Anda akan secara bertahap mulai mempelajari cara berpikir matematika. Jika Anda memahami matematika yang Anda operasikan dengan benar, maka Anda akan memahaminya dengan lebih baik. Oleh karena itu, saya tidak mencoba untuk menghindari matematika nyata, tetapi lebih tepatnya, menjelaskannya langkah demi langkah, sehingga semua matematika secara bertahap menjadi jelas bagi Anda. Seperti banyak orang, saya pernah percaya bahwa matematika adalah ilmu yang rumit, dan sulit untuk bekerja dengannya. Seiring waktu, saya menjadi yakin bahwa dengan pendekatan yang tepat, matematika tidak menyebabkan hampir semua kesulitan. Setiap kebingungan dalam matematika biasanya muncul hanya karena upaya untuk melewati materi terlalu cepat - karena ini, langkah-langkah penting yang diperlukan untuk penalaran yang tepat tidak terjawab.

3. Mengapa seorang programmer mempelajari teori probabilitas dan statistik?

Saya benar-benar percaya bahwa setiap orang harus mempelajari teori probabilitas dan statistik sampai batas tertentu, karena pengetahuan ini akan membantu menilai ketidakpastian yang mengelilingi kita di mana pun dalam kehidupan. Sedangkan untuk programmer, ia pasti harus berurusan dengan beberapa tugas khas di mana berguna untuk memahami statistik. Sangat mungkin bahwa, pada titik tertentu dalam karir profesional Anda, Anda harus menulis kode di mana beberapa keputusan dibuat berdasarkan faktor fuori priori. Mungkin ini akan menjadi ukuran konversi halaman web, generasi beberapa hadiah acak dalam game, distribusi acak pengguna ke dalam grup, atau bahkan membaca informasi dari beberapa sensor fuzzy. Dalam semua kasus ini, pemahaman yang kuat tentang teori probabilitas akan banyak membantu Anda. Praktik saya sendiri menunjukkan bahwa pendekatan probabilistik banyak membantu dalam men-debug banyak bug yang sulit direproduksi atau dilacak ke masalah yang kompleks. Jika ternyata bug tersebut disebabkan oleh memori yang tidak mencukupi, dapatkah Anda yakin bahwa bug tersebut akan lebih sering terjadi jika memori terpotong lebih keras? Jika bug yang rumit dapat dijelaskan dengan dua cara, lalu apa peluang terbaik untuk dijelajahi terlebih dahulu? Dalam semua kasus seperti itu, teori probabilitas dapat membantu. Tentu saja, masa kejayaan pembelajaran mesin dan Ilmu Data mengarah pada fakta bahwa para insinyur semakin harus berurusan dengan tugas-tugas di mana pemrograman menawarkan kerja langsung dengan probabilitas.

4. Apakah mungkin untuk menggambarkan secara singkat perbedaan antara frekuensi dan pendekatan Bayesian terhadap teori probabilitas?

Dalam interpretasi frekuensi, probabilitas ditafsirkan sebagai pernyataan tentang seberapa sering suatu peristiwa harus terjadi selama upaya berulang. Jadi, melempar koin dua kali, orang harus berharap bahwa itu akan dijatuhkan oleh elang 1 kali, karena koin memiliki dua sisi, dan salah satunya memiliki elang. Dalam interpretasi Bayesian, probabilitas ditafsirkan sebagai beberapa karakteristik pengetahuan kita, pada prinsipnya, sebagai kelanjutan dari logika. Peluang melempar koin dengan rajawali adalah 0,5, karena saya tidak melihat alasan mengapa rajawali lebih sering jatuh daripada ekor. Jadi, dalam kasus lemparan koin, kedua pendekatan berfungsi penuh. Namun, ketika hal-hal seperti peluang tim favorit Anda memenangkan Piala Dunia, faktor kepercayaan diri menjadi jauh lebih signifikan. Omong-omong, ini juga berarti bahwa statistik Bayesian membuat pernyataan bukan tentang dunia, tetapi tentang pemahaman kita tentang dunia. Karena setiap orang memahami dunia sedikit berbeda, statistik Bayesian membantu kita memperhitungkan perbedaan-perbedaan ini dalam analisis kita. Dalam banyak hal, analisis Bayesian adalah ilmu tentang evolusi pendapat.

5. Mengapa fokus buku ini pada pendekatan Bayesian?

Ada banyak alasan filosofis yang sangat bagus untuk berfokus pada statistik Bayesian, tetapi saya dibimbing oleh alasan yang sepenuhnya praktis: dengan pendekatan Bayesian, semuanya menjadi logis. Berdasarkan seperangkat aturan intuitif yang relatif kecil, Anda dapat mengembangkan solusi untuk hampir semua masalah yang mungkin Anda temui. Inilah sebabnya mengapa statistik Bayesian begitu kuat dan fleksibel, dan mengapa mudah dipelajari. Saya pikir cara Bayesian beralasan sesuai dengan programmer. Anda tidak mencoba untuk memecahkan masalah dengan bantuan tes dadakan, tetapi Anda beralasan dan secara bertahap datang ke solusi yang benar-benar dibenarkan. Pada prinsipnya, statistik Bayesian - ini adalah alasannya. Anda setuju dengan analisis statis hanya jika itu benar-benar logis dan meyakinkan Anda, dan bukan karena tes Anda yang terlihat sewenang-wenang memberi Anda beberapa nilai yang sama sekali tidak berdasar. Selain itu, statistik Bayesian memungkinkan untuk meragukan hasil dan dari sudut pandang kualitatif. Dalam praktik sehari-hari, sering terjadi bahwa dua orang disajikan dengan fakta yang sama, tetapi kesimpulan mereka berbeda. Statistik Bayesian memungkinkan kita untuk memodelkan perbedaan pendapat secara formal, sehingga kita dapat memeriksa sendiri fakta apa yang akan dibutuhkan sehingga kita mengubah sudut pandang kita. Anda tidak harus mempercayai hasil yang dinyatakan di atas kertas karena beberapa nilai-p, Anda mempercayainya, karena menurut Anda itu sangat meyakinkan.

6. Bagaimana statistik Bayesian berhubungan dengan pembelajaran mesin

Di antara kesamaan antara pembelajaran mesin (khususnya, jaringan saraf) dan statistik Bayesian yang telah saya pikirkan adalah sebagai berikut: dalam kedua disiplin ilmu ini, analisis matematika bisa sangat rumit. Pada prinsipnya, pembelajaran mesin adalah pemahaman dan solusi dari turunan yang sangat sepele. Anda mendapatkan fungsi, dan untuk itu, fungsi kerugian, lalu (secara otomatis) menghitung turunan dan mencoba untuk mengikutinya sampai itu membawa Anda ke parameter optimal. Banyak yang dengan jahat mencatat bahwa propagasi mundur hanyalah "aturan rantai", tetapi di hampir semua tugas kompleks yang terkait dengan pembelajaran mesin, digunakan sangat berhasil.
Statistik Bayesian adalah aspek lain dari analisis matematika yang terkait dengan penyelesaian integral yang benar-benar kompleks. Michael Betancourt, penulis Stan, dengan sempurna mencatat bahwa hampir semua analisis Bayesian terhubung dengan perhitungan ekspektasi, yaitu dengan perhitungan integral. Sebagai hasil dari analisis Bayesian, Anda masih memiliki distribusi posterior, tetapi Anda tidak dapat menggunakannya dengan cara apa pun tanpa mengintegrasikannya dan dengan demikian tidak mendapatkan jawaban yang konkret. Untungnya, tidak ada yang membuat komentar jahat tentang integral, karena semua orang tahu bahwa bahkan integral yang paling sepele pun cukup rumit. Berikut adalah bagaimana itu diformulasikan secara aphoristically di salah satu komik xkcd:



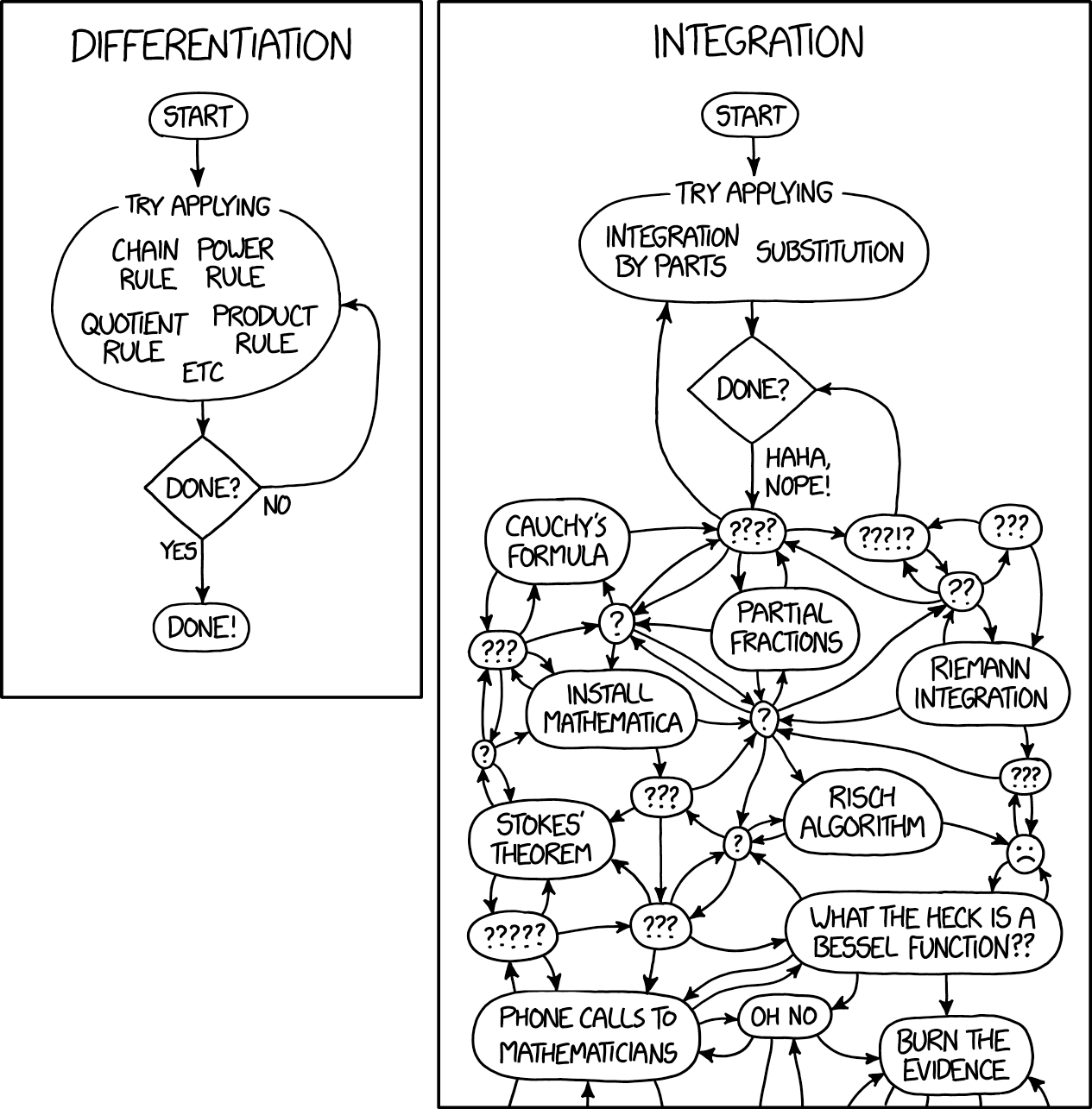
Saat ini, pembelajaran mesin dan statistik Bayesian berada dalam keadaan yang sangat aneh: kami mengembangkan ide-ide paling sederhana dari analisis matematika hingga tingkat kompleksitas yang hanya cocok untuk komputasi.

Hubungan ini juga menyoroti satu poin kunci. Ketika kita berbicara tentang turunan, kita mencari titik tertentu yang terkait dengan suatu fungsi. Jadi, jika Anda tahu posisi dan waktu, maka kecepatan adalah turunan yang seharusnya menentukan kapan Anda bergerak paling cepat. Langkah kecil menuju kemajuan MO adalah ketika Anda mengetahui bahwa satu metrik lebih baik daripada orang lain. Integrasi adalah penjumlahan dari keseluruhan proses. Sekali lagi, jika Anda tahu tempat dan waktu, maka integral adalah jarak, itu memungkinkan Anda untuk mengetahui seberapa jauh Anda telah datang. Statistik Bayesian adalah ringkasan dari segala sesuatu yang Anda ketahui tentang suatu masalah, tetapi memungkinkan Anda tidak hanya untuk membuat prakiraan terpisah, tetapi juga untuk mengkarakterisasi tingkat kepercayaan pada prakiraan kami, yang berada dalam berbagai pilihan. Kemajuan dalam statistik Bayesian adalah pemahaman tentang sistem informasi yang semakin kompleks.

7. Jika pembaca ingin lebih mengenal topik buku ini, materi apa (buku, kursus, blog) yang akan Anda beri tahu?

Saya mengambil inspirasi maksimal dari buku I. T. Jane "Probability Theory: the Logic of Science". Diam-diam, saya berharap bahwa buku saya "statistik Bayesian hebat" dapat menjadi analog dari bukunya, tetapi ditujukan untuk pembaca yang luas. Bekerja dengan buku Janes bukanlah tugas yang mudah, dan menyajikan hasil yang sangat radikal dari statistik Bayesian. Aubrey Clayton melakukan pelayanan yang adil kepada para pembacanya dengan menulis serangkaian ceramah tentang bab-bab buku ini.

Tentu saja, jika Anda menyukai buku itu, maka Anda mungkin akan menyukai blog saya. Baru-baru ini, saya tidak menulis begitu banyak di sana, karena saya menulis buku "statistik Bayesian hebat", dan sebelum itu "Dapatkan Pemrograman dengan Haskell", tetapi sekarang saya memiliki kepala yang penuh ide, dan tidak semua dari mereka dikhususkan secara ketat untuk Bayesian topik. Sebagai aturan, saya merefleksikan topik dari bidang statistik / probabilitas, dan dari ide ini saya dengan hati-hati memilih artikel baru untuk blog.

8. Dalam pengalaman Anda, konsep mana dalam bidang teori probabilitas / statistik yang sulit dipahami?

Jujur, bagian tersulit adalah interpretasi probabilitas. Orang-orang benar-benar kehilangan kepercayaan pada banyak analis Bayesian, seperti Nate Silver (dan banyak lainnya), ketika mereka meramalkan bahwa Hillary Clinton akan memenangkan pemilu 2016 dengan probabilitas 80% - dan dia kalah. Orang-orang berpikir bahwa seseorang telah menipu mereka, dan semua orang salah, tetapi, pada kenyataannya, probabilitas 80% tidak begitu banyak. Jika dokter memberi tahu saya bahwa peluang saya untuk bertahan hidup adalah 80%, maka saya sangat gugup.

Sebagai aturan, masalah ini diselesaikan sebagai berikut: kami menunjukkan probabilitas seperti itu dan menyatakan bahwa mereka tidak cocok untuk mengekspresikan ketidakpastian. Untuk mengatasi ketidaknyamanan ini, kita harus menggunakan koefisien atau kemungkinan rasio, atau semacam sistem desibel, seperti konsep Jane "bukti". Namun, setelah memikirkan probabilitas untuk waktu yang lama, saya sampai pada kesimpulan bahwa tidak ada cara unik yang cocok untuk mengekspresikan ketidakpastian.

Inti dari masalahnya adalah kita masing-masing yakin bahwa ada kepastian di dunia. Bahkan spesialis berpengalaman dalam teori probabilitas memiliki perasaan bahwa, jika Anda melakukan analisis yang benar, mencari tahu data apriori yang diperlukan, menambahkan level lain ke model hierarkis Anda, Anda akan berhasil, dan Anda akan menyingkirkan ketidakpastian atau setidaknya menguranginya . Peluang sebagian menarik bagi saya karena kombinasi aneh dari dua faktor ini: keinginan untuk memahami dunia dan pengakuan bahwa, tidak peduli bagaimana Anda mencoba, dunia tetap akan mengejutkan Anda.

9. Apa yang Anda pikirkan tentang nilai-p sebagai ukuran signifikansi statistik? Bisakah Anda jelaskan secara singkat apa itu p-hacking?

Dalam hal nilai-p, dua hal sering disalahpahami. Pertama, orang yang cerdas tidak akan mencoba menjawab pertanyaan dengan nilai-p. Bayangkan seperti apa percakapan berikut di tempat kerja:

Manajer: "Anda memperbaiki bug ini, bagaimana itu ditugaskan kepada Anda?"
Anda: "Yah, saya lebih dari yakin saya tidak memperbaikinya ..."
Manajer: "Jika Anda memperbaikinya, tandai bahwa Anda telah memperbaikinya."
Anda: "Oh, tidak, saya tidak bisa mengatakan bahwa saya memperbaikinya ..."
Manajer: "Nah, apakah Anda akan menandainya 'Saya tidak akan memperbaikinya'?"
Anda: "Tidak, tidak, tentu saja tidak seperti itu sama sekali"

Nilai-p banyak yang bingung, karena mereka secara inheren tidak jelas. Statistik Bayesian memberi tahu Anda kemungkinan posterior, yang merupakan jawaban positif untuk pertanyaan yang dirumuskan sesuka Anda. Dalam dialog di atas, Bayesian mengatakan: "Saya cukup yakin bug telah diperbaiki." Jika manajer ingin Anda merespons lebih percaya diri, maka Bayesian dapat mengumpulkan informasi tambahan dan berkata: "Saya, pada prinsipnya, yakin bahwa itu diperbaiki."

Masalah kedua adalah kebiasaan yang sudah tertanam dalam memilih 0,05 sebagai semacam makna magis, yang konon bermakna. Kembali ke pertanyaan sebelumnya tentang memahami probabilitas, probabilitas 5% bahwa peristiwa tertentu akan terjadi tidak berarti bahwa peristiwa ini jarang terjadi. Anda akan memiliki peluang 5% untuk mendapatkan 20 poin saat melempar dadu 20 sisi. Namun, siapa pun yang telah memainkan Dungeons and Dragons tahu bahwa ini jauh dari mustahil. Di luar RPG, melempar tulang bukanlah alat terbaik untuk membedakan kebenaran dari kebohongan.

Di sini kita sampai pada p-hacking. Bayangkan Anda bermain Dungeons and Dragons dengan teman-teman Anda dan Anda melempar 20 dadu sekaligus. Lalu Anda menunjuk ke titik di mana 20 poin jatuh, dan menyatakan: "inilah tulang yang akan saya lempar, dan sisanya adalah yang tes." Secara formal, Anda benar-benar mencetak 20 poin, tetapi ini masih scam, Anda tahu. Ini adalah inti dari peretasan. Anda melakukan analisis sampai Anda menemukan sesuatu yang "penting", dan kemudian Anda mengklaim bahwa inilah yang Anda cari sejak awal.

10. Rekomendasi akhir tentang buku mana yang harus dibaca setelah Anda?

, , , , . «Bayesian Analysis with Python» (, Not Monad Tutorial). , PyMC3. , . , — “Statistical Rethinking” . , . . « – ». , «Doing Bayesian Data Analysis» .