Kami menulis "kalkulator" dalam C #. Bagian I. Perhitungan nilai, turunan, penyederhanaan, dan angsa lainnya

Hai

Untuk beberapa alasan, kalkulator kami dikaitkan dengan sesuatu yang harus ditulis oleh setiap pemula. Mungkin karena secara historis komputer untuk tujuan itu diciptakan untuk dihitung. Tetapi kami akan menulis kalkulator yang sulit, tentu saja bukan sympy, tetapi untuk dapat melakukan operasi aljabar dasar, seperti diferensiasi, penyederhanaan, dan fitur seperti kompilasi untuk mempercepat perhitungan.


Kami mengambil cookie yang tersisa dari tahun baru, dan melaju!

Perakitan ekspresi

Apa itu ekspresi?

Tentu saja, ini bukan garis. Cukup jelas bahwa rumus matematika adalah pohon atau tumpukan, dan di sini kita berhenti di yang pertama. Artinya, setiap node, setiap node dari pohon ini, adalah semacam operasi, variabel, atau konstanta.



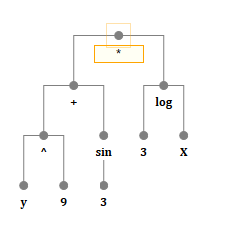
Operasi adalah fungsi atau operator, pada prinsipnya, kira-kira sama. Anak-anaknya adalah argumen dari suatu fungsi (operator).

Hirarki kelas dalam kode Anda

Tentu saja implementasinya bisa apa saja. Namun, idenya adalah jika pohon Anda hanya terdiri dari node dan daun, maka mereka berbeda. Karena itu, saya menyebutnya "benda" - entitas. Oleh karena itu, kelas atas akan menjadi Entitas kelas abstrak.


Dan juga akan ada empat kelas penerus: NumberEntity, VariableEntity, OperatorEntity, FunctionEntity.

Bagaimana cara membangun ekspresi?

Pertama, kita akan membangun ekspresi dalam kode, mis.

var x = new VariableEntity("x"); var expr = x * x + 3 * x + 12; 

Jika Anda mendeklarasikan VariableEntity kelas kosong, maka kode seperti itu akan membuat Anda mengalami kesalahan, kata mereka tidak tahu bagaimana cara mengalikan dan menjumlahkan.

Operator Overriding

Fitur yang sangat penting dan berguna dari sebagian besar bahasa, memungkinkan Anda untuk menyesuaikan pelaksanaan operasi aritmatika. Secara sintaksis diimplementasikan secara berbeda tergantung pada bahasanya. Misalnya, implementasi di C #

 public static YourClass operator +(YourClass a, YourClass b) { return new YourClass(a.ToString() + b.ToString()); } 

Pelajari lebih lanjut tentang mengganti pernyataan dalam C #
Lobak diimplementasikan di sini .

(Non) casting eksplisit

Dalam bahasa yang dikompilasi seperti C #, hal seperti itu biasanya ada dan memungkinkan Anda untuk mengetikkan jenisnya jika perlu tanpa tambahan memanggil myvar.ToAnotherType (). Jadi, misalnya, akan lebih mudah untuk menulis

 NumberEntity myvar = 3; 

Alih-alih biasa

 NumberEntity myvar = new NumberEntity(3); 

Lebih lanjut tentang tipe casting di C #
Lobak diimplementasikan pada baris ini .

Menggantung

Kelas Entity memiliki bidang Children - ini hanya daftar Entity, yang merupakan argumen untuk entitas ini.


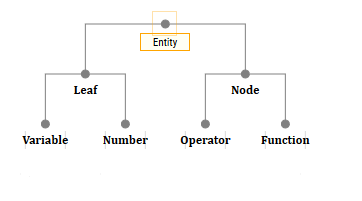
Ketika kita memanggil fungsi atau operator, kita harus membuat entitas baru, dan memasukkannya anak-anak dari mana fungsi atau operator dipanggil. Misalnya, jumlah dalam teori seharusnya terlihat seperti ini:

 public static Entity operator +(Entity a, Entity b){ var res = new OperatorEntity("+"); res.Children.Add(a); res.Children.Add(b); return res; } 

Yaitu, sekarang jika kita memiliki entitas x dan entitas 3, maka x + 3 akan mengembalikan esensi dari operator penjumlahan dengan dua anak: 3 dan x. Jadi, kita bisa membangun pohon ekspresi.

Panggilan fungsi lebih sederhana dan tidak seindah dengan operator:

 public Entity Sin(Entity a) { var res = new FunctionEntity("sin"); res.Children.Add(a); return res; } 

Hanging in lobak diterapkan di sini .

Oke, kami membuat pohon ekspresi.

Substitusi variabel

Semuanya sangat sederhana di sini. Kami memiliki Entitas - kami memeriksa apakah itu variabel itu sendiri, jika demikian, kami mengembalikan nilainya, jika tidak, kami dijalankan melalui anak-anak.

File besar 48-baris ini mengimplementasikan fungsi yang begitu rumit.

Perhitungan nilai

Sebenarnya, untuk apa semua ini. Di sini kita seharusnya menambahkan semacam metode ke Entity

 public Entity Eval() { if (IsLeaf) { return this; } else return MathFunctions.InvokeEval(Name, Children); } 

Daunnya tidak berubah, tetapi untuk semua yang lain kami memiliki perhitungan khusus. Sekali lagi, saya akan memberikan contoh saja:

 public static Entity Eval(List<Entity> args) { MathFunctions.AssertArgs(args.Count, 1); var r = args[0].Eval(); if (r is NumberEntity) return new NumberEntity(Number.Sin((r as NumberEntity).Value)); else return r.Sin(); } 

Jika argumennya berupa angka, maka kami akan menghasilkan fungsi numerik, jika tidak kami akan mengembalikannya seperti semula.

Angka?

Ini adalah unit paling sederhana, angka. Operasi aritmatika dapat dilakukan di atasnya. Secara default, ini rumit. Dia juga memiliki operasi seperti Dosa, Cos, dan beberapa yang lainnya.

Jika tertarik, Nomor dijelaskan di sini .

Derivatif

Siapa pun dapat menghitung turunannya secara numerik, dan fungsi seperti itu ditulis dengan benar dalam satu baris:

 public double Derivative(Func<double, double> f, double x) => (f(x + 1.0e-5) - f(x)) * 1.0e+5; 

Tapi tentu saja kami menginginkan turunan analitik. Karena kita sudah memiliki pohon ekspresi, kita dapat secara rekursif mengganti setiap node sesuai dengan aturan diferensiasi. Seharusnya berfungsi seperti ini:



Di sini, misalnya, bagaimana jumlah diterapkan dalam kode saya:

 public static Entity Derive(List<Entity> args, VariableEntity variable) { MathFunctions.AssertArgs(args.Count, 2); var a = args[0]; var b = args[1]; return a.Derive(variable) + b.Derive(variable); } 

Tetapi pekerjaan

 public static Entity Derive(List<Entity> args, VariableEntity variable) { MathFunctions.AssertArgs(args.Count, 2); var a = args[0]; var b = args[1]; return a.Derive(variable) * b + b.Derive(variable) * a; } 

Dan ini adalah solusinya sendiri:

 public Entity Derive(VariableEntity x) { if (IsLeaf) { if (this is VariableEntity && this.Name == x.Name) return new NumberEntity(1); else return new NumberEntity(0); } else return MathFunctions.InvokeDerive(Name, Children, x); } 

Ini adalah metode Entity. Dan seperti yang kita lihat, daun hanya memiliki dua status - baik itu variabel yang kita bedakan, maka turunannya adalah 1, atau itu adalah konstanta (angka atau Variabel), maka turunannya adalah 0, atau simpul, maka ada referensi dengan nama (InvokeDerive merujuk ke kamus fungsi, di mana yang diinginkan berada (misalnya, jumlah atau sinus)).

Perhatikan bahwa saya tidak meninggalkan sesuatu seperti dy / dx di sini dan langsung mengatakan bahwa turunan dari variabel yang tidak kita bedakan adalah 0. Tapi di sini dilakukan secara berbeda.

Semua diferensiasi dijelaskan dalam satu file , tetapi lebih banyak tidak diperlukan.

Penyederhanaan ekspresi. Pola

Penyederhanaan ungkapan pada prinsipnya umumnya tidak sepele. Misalnya, ungkapan mana yang lebih sederhana: $$$x ^ 2 - y ^ 2$atau $$$(x - y) (x + y)$? Tetapi kami mematuhi beberapa ide, dan atas dasar itu kami ingin membuat aturan-aturan yang secara akurat menyederhanakan ekspresi.

Dimungkinkan untuk menulis di setiap Eval bahwa jika kami memiliki jumlah, dan anak-anak bekerja, maka kami akan memilah empat opsi, dan jika ada sesuatu yang sama di suatu tempat, kami akan mengambil faktornya ... Tapi tentu saja saya tidak ingin melakukan itu. Karena itu, Anda bisa menebak sistem aturan dan pola. Jadi apa yang kita inginkan? Sesuatu seperti sintaks ini:

 { any1 / (any2 / any3) -> any1 * any3 / any2 }, { const1 * var1 + const2 * var1 -> (const1 + const2) * var1 }, { any1 + any1 * any2 -> any1 * (Num(1) + any2) }, 

Berikut adalah contoh pohon tempat subtree ditemukan (dilingkari hijau) yang cocok dengan pola any1 + const1 * any1 (any1 ditemukan dilingkari dengan warna oranye).



Seperti yang Anda lihat, terkadang penting bagi kami bahwa satu dan entitas yang sama harus diulang, misalnya, untuk mengurangi ekspresi x + a * x, kita perlu x untuk berada di sana dan di sana, karena x + a * y tidak lagi berkurang. Oleh karena itu, kita perlu membuat algoritma yang tidak hanya memeriksa bahwa pohon cocok dengan pola, tetapi juga

1. Verifikasi bahwa pola Entitas yang sama cocok dengan Entitas yang sama.
2. Untuk menuliskan apa yang sesuai dengan apa, lalu untuk mengganti.

Titik masuknya terlihat seperti ini:

 internal Dictionary<int, Entity> EqFits(Entity tree) { var res = new Dictionary<int, Entity>(); if (!tree.PatternMakeMatch(this, res)) return null; else return res; } 

Dan di tree.PaternMakeMatch, kami mengisi kamus dengan kunci dan nilainya secara rekursif. Berikut adalah contoh daftar Entitas pola itu sendiri:

 static readonly Pattern any1 = new Pattern(100, PatType.COMMON); static readonly Pattern any2 = new Pattern(101, PatType.COMMON); static readonly Pattern const1 = new Pattern(200, PatType.NUMBER); static readonly Pattern const2 = new Pattern(201, PatType.NUMBER); static readonly Pattern func1 = new Pattern(400, PatType.FUNCTION); 

Ketika kita menulis any1 * const1 - func1 dan seterusnya, setiap node akan memiliki nomor - ini adalah kuncinya. Dengan kata lain, ketika mengisi kamus, angka-angka ini akan muncul sebagai kunci: 100, 101, 200, 201, 400 ... Dan ketika membangun pohon, kita akan melihat nilai yang sesuai dengan kunci dan menggantinya.

Diimplementasikan di sini .

Penyederhanaan. Penyortiran pohon

Dalam artikel yang telah saya bahas, penulis memutuskan untuk melakukannya secara sederhana, dan diurutkan secara praktis berdasarkan hash of the tree. Dia berhasil mengurangi a dan -a, b + c + b untuk mengubah 2b + c. Tapi kami, tentu saja, juga ingin (x + y) + x * y - 3 * x dikurangi, dan secara umum hal-hal yang lebih rumit.

Pola tidak berfungsi?

Secara umum, apa yang kami lakukan sebelumnya, pola adalah hal yang sangat indah. Ini akan memungkinkan Anda untuk mengurangi perbedaan antara kotak, dan jumlah kuadrat dari sinus dan kosinus, dan hal-hal kompleks lainnya. Tetapi palm elementer, (((((x + 1) + 1) + 1) + 1), tidak akan berkurang, karena aturan utama di sini adalah komutatifitas istilah-istilah tersebut. Oleh karena itu, langkah pertama adalah mengisolasi "anak-anak linier."

"Anak linear"

Sebenarnya, untuk setiap simpul jumlah atau perbedaan (dan, omong-omong, produk / divisi), kami ingin mendapatkan daftar istilah (faktor).



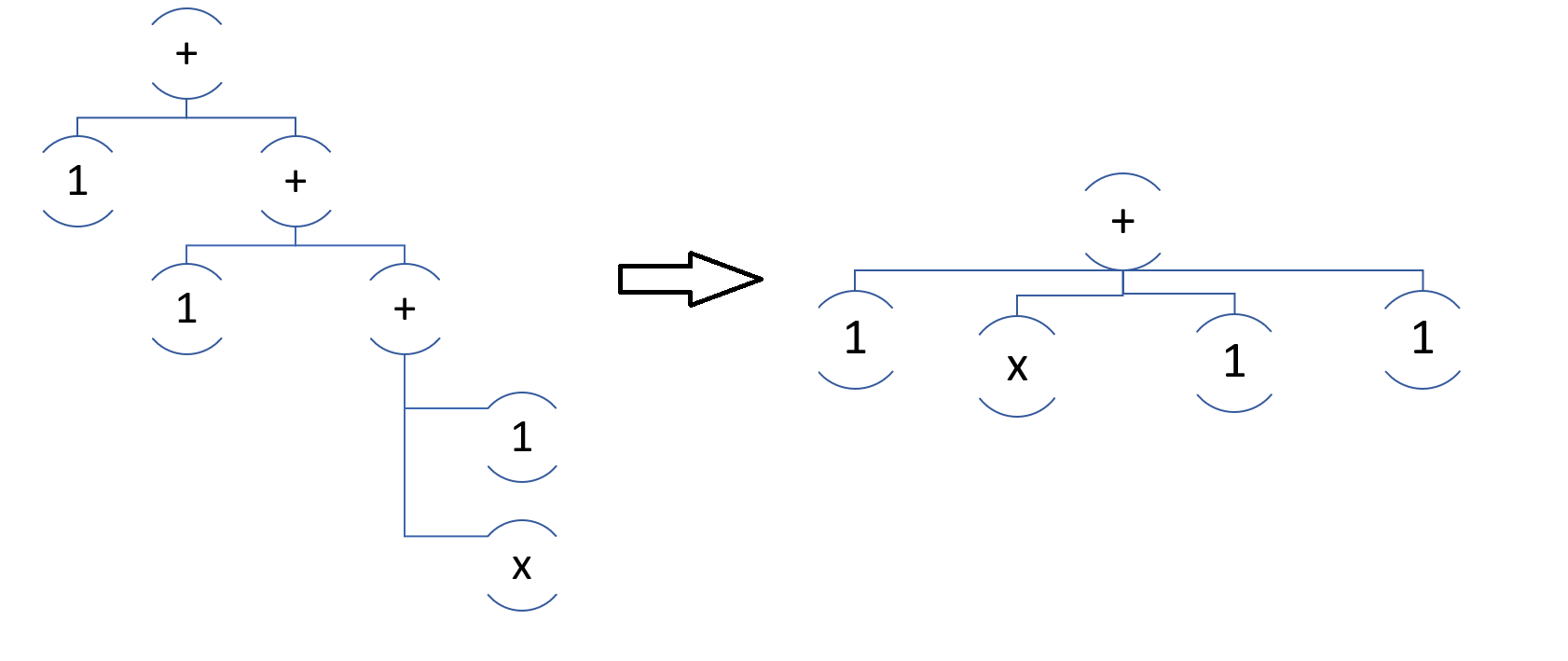
Ini pada dasarnya mudah. Biarkan fungsi LinearChildren (Entity node) mengembalikan daftar, maka kita melihat child di node.Children: jika child bukan penjumlahan, maka result.Add (child), jika tidak result.AddRange (LinearChildren (child)).

Bukan cara terindah yang diterapkan di sini .

Mengelompokkan anak-anak

Jadi kami punya daftar anak-anak, tetapi bagaimana selanjutnya? Misalkan kita memiliki dosa (x) + x + y + dosa (x) + 2 * x. Jelas, algoritma kami akan menerima lima istilah. Selanjutnya, kami ingin mengelompokkan berdasarkan kesamaan, misalnya, x terlihat 2 * x lebih dari dosa (x).

Ini adalah pengelompokan yang bagus:



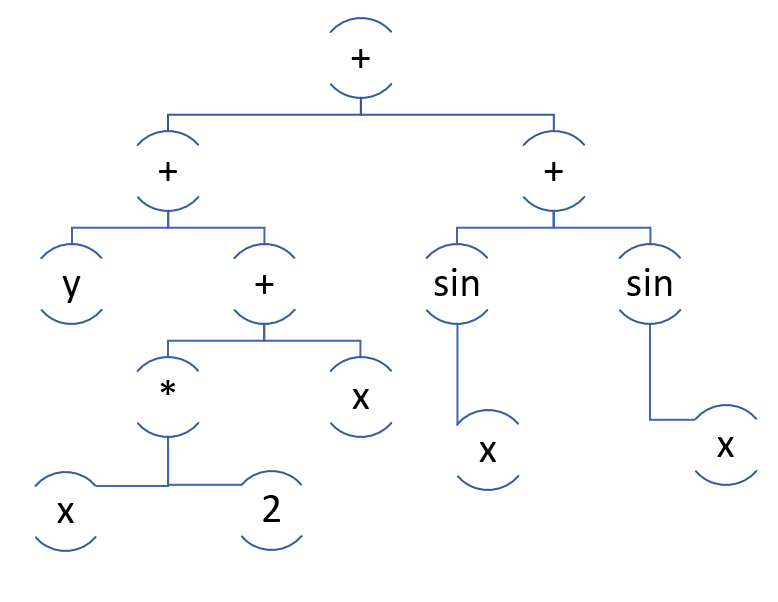
Karena pola di dalamnya akan mengatasi lebih lanjut dengan konversi 2 * x + x ke 3 * x.

Yaitu, kita pertama-tama mengelompokkan beberapa hash , dan kemudian melakukan MultiHang - mengonversi penjumlahan n-ary menjadi biner.

Hash simpul

Di satu sisi $$$x$dan $$$x + 1$harus ditempatkan dalam satu kelompok. Di sisi lain, jika tersedia $$$a * x$dimasukkan ke dalam satu grup dengan $$$y * (x + 1)$sia-sia


Oleh karena itu, kami menerapkan penyortiran multi-level. Pertama, kami berpura-pura $$$x + 1$- hal yang sama. Diurutkan, tenang. Lalu kami berpura-pura $$$x + 1$hanya bisa ditempatkan dengan orang lain $$$x + 1$. Dan sekarang milik kita $$$a * (x + 1)$dan $$$y * (x + 1)$akhirnya bergabung. Diimplementasikan dengan sederhana:

 internal string Hash(SortLevel level) { if (this is FunctionEntity) return this.Name + "_" + string.Join("_", from child in Children select child.Hash(level)); else if (this is NumberEntity) return level == SortLevel.HIGH_LEVEL ? "" : this.Name + " "; else if (this is VariableEntity) return "v_" + Name; else return (level == SortLevel.LOW_LEVEL ? this.Name + "_" : "") + string.Join("_", from child in Children where child.Hash(level) != "" select child.Hash(level)); } 

Seperti yang Anda lihat, fungsi memengaruhi penyortiran dengan cara apa pun (tentu saja, karena $$$f (x)$dengan $$$x$umumnya tidak terhubung dalam kasus umum). Seperti variabel, $$$x$dengan $$$y$Yah, itu tidak berhasil bergaul. Tetapi konstanta dan operator tidak diperhitungkan di semua tingkatan. Dalam urutan ini, proses penyederhanaan itu sendiri

 public Entity Simplify(int level) { //      :   ,   ,     . . var stage1 = this.InnerSimplify(); Entity res = stage1; for (int i = 0; i < level; i++) { //     .    -  x  x+1 (  ),  -  x-1  x+1 (,   ),  -  x+1  x+1 ( ). switch (i) { case 0: res = res.Sort(SortLevel.HIGH_LEVEL); break; case 2: res = res.Sort(SortLevel.MIDDLE_LEVEL); break; case 4: res = res.Sort(SortLevel.LOW_LEVEL); break; } //    . res = TreeAnalyzer.Replace(Patterns.CommonRules, res).InnerSimplify(); } return res; } 

Saya menyortir pohon di sini .

"Kompilasi" fungsi

Dalam tanda kutip - karena tidak ada dalam kode IL itu sendiri, tetapi hanya dalam set instruksi yang sangat cepat. Tapi ini sangat sederhana.

Masalah Pengganti

Untuk menghitung nilai fungsi, kita hanya perlu memanggil subtitusi variabel dan eval, misalnya

 var x = MathS.Var("x"); var expr = x * x + 3; var result = expr.Substitute(x, 5).Eval(); 

Tapi itu bekerja lambat, sekitar 1,5 mikrodetik per sinus.

Instruksi

Untuk mempercepat perhitungan, kami melakukan perhitungan fungsi pada stack, yaitu:

1) Kami datang dengan kelas FastExpression, yang akan memiliki daftar instruksi

2) Ketika mengkompilasi, instruksi ditumpuk dalam urutan terbalik, yaitu, jika ada fungsi x * x + sin (x) + 3, maka instruksi akan menjadi seperti ini:

 PUSHVAR 0 //    0 - x CALL 6 //    6 -  PUSHCONST 3 CALL 0 //    0 -  PUSHVAR 0 PUSHVAR 0 CALL 2 CALL 0 

Selanjutnya, ketika dipanggil, kami menjalankan instruksi ini dan mengembalikan Nomor.

Contoh mengeksekusi pernyataan jumlah:

 internal static void Sumf(Stack<Number> stack) { Number n1 = stack.Pop(); Number n2 = stack.Pop(); stack.Push(n1 + n2); } 

Panggilan sinus dikurangi dari 1500ns menjadi 60ns (sistem Complex.Sin bekerja untuk 30ns).
Lobak diimplementasikan di sini .

Fuh, semuanya sepertinya untuk saat ini. Meskipun masih ada sesuatu untuk diceritakan, tetapi bagi saya tampaknya volume untuk satu artikel sudah cukup. Adakah yang tertarik dengan sekuelnya? Yaitu: parsing dari string, memformat dalam lateks, integral tertentu, dan barang lainnya.

Tautkan ke repositori dengan semua kode, serta tes dan sampel.


Terima kasih atas perhatian anda!