Simulasi berlari di tengah hujan

Entri

Semuanya dimulai dengan pernyataan yang sangat provokatif yang berbatasan dengan keberanian, yang pasti tidak sesuai dengan ide saya tentang dunia di sekitar saya: "Anda bisa lebih basah jika berlari di tengah hujan - ini adalah mitos." Dengan kata lain, dari pernyataan ini diketahui bahwa telah diketahui dan diterima secara umum bahwa seseorang yang berlari di tengah hujan akan lebih basah daripada orang yang sama yang berjalan pada jarak yang sama dengan berjalan kaki, dalam hujan yang sama. Tetapi, beberapa sumber yang tidak dapat dipercaya yang tidak dapat dipercaya mengklaim sebaliknya, bahwa jika Anda segera keluar dari hujan, hujan Anda akan berkurang.

Pernyataan ini dibuat di program televisi Mythbusters (episode 001). Saya memeriksa ulang beberapa kali - kata-kata dalam mitos ini persis seperti ini: "Seseorang akan berakhir lebih kering dengan berlari di tengah hujan daripada berjalan."
_{Pembaruan: seperti yang disarankan rezdm ada video dengan kata-kata yang berbeda “Apakah layak dijalankan di tengah hujan”}

Selain itu, hasil verifikasi adalah penghancuran mitos ini, yaitu, pemimpin yang berlari basah lebih kuat dari pemimpin yang berjalan!? Yaitu, sumber-sumber yang tidak dapat diverifikasi dan tidak dapat dipercaya ini, dengan kebodohan mereka, diberlakukan. Sampai saat itu, di duniaku semuanya terbalik, dan agar tidak terlalu basah, aku mencoba lari ke tempat berlindung.

Selanjutnya, beberapa musim kemudian, mitos ini diperiksa ulang dan dibantah (episode 38). Tetapi hasil dalam kedua kasus pertama dan kedua tidak terlalu mengungkapkan: perbedaan dalam air yang dikumpulkan kecil, dan hampir tidak sangat berbeda dari kesalahan statistik, dan dari kesalahan pengukuran pada keseimbangan. Dalam percobaan pertama, hujan diciptakan dengan memasok air ke alat penyiram yang menggantung dari langit-langit hanggar yang tinggi. Dalam percobaan kedua, mereka bekerja dengan apa yang akan jatuh dari langit. Setelah percobaan kedua, kejelasan menjadi lebih sedikit.

Saya lebih menyukai percobaan pertama, karena ada kondisi yang terkendali, dan kondisi ini dapat dipertahankan untuk waktu yang diperlukan. Dalam kasus hujan biasa, kondisinya terus berubah - hujan mungkin berhenti, intensitasnya mungkin berubah atau angin akan bertiup. Menurut pendapat saya, perlu untuk melanjutkan studi pertama: Anda bisa meningkatkan jarak, Anda bisa bermain dengan parameter hujan untuk mengurangi kesalahan statistik dan membuat hasilnya lebih meyakinkan. Mythbusters adalah program televisi yang sangat baik, tetapi dalam kasus khusus ini saya ingin mengambil dan mengulang semuanya. Terutama tertarik pada tema pengaruh sifat hujan pada hujan yang dihasilkan, karena biasanya dalam eksperimen tersebut ada hujan rata-rata, dan bagaimanapun hujan berbeda.

Seperti yang biasanya terjadi, saya dengan berani mengatasi keinginan yang tidak masuk akal ini, memaksakan keinginan untuk membuat kembali percobaan dan melupakannya. Tetapi musim panas tahun ini di wilayah Moskow sepertinya terlalu sering memikirkan "apakah saya harus lari dari hujan ini, atau pergi dengan tenang." Akibatnya, saya memutuskan untuk menulis proyek kecil dan mengeksplorasi apa yang menarik dengan bantuan pemodelan komputer. Ternyata, di wilayah Moskow topik ini tetap relevan sekarang di bulan Desember.

Bagian selanjutnya menjelaskan apa yang terjadi, tetapi di sini saya perlu mengatakan beberapa kata tentang sejarah masalah ini. Dalam mempersiapkan artikel itu, ternyata pertanyaan "berjalan atau berlari di tengah hujan" telah menghantui banyak geek di seluruh dunia selama beberapa waktu. Rupanya, gelombang pertama yang muncul adalah popularizer ilmu pengetahuan yang terkenal, Yakov Isidovich Perelman, dalam bukunya "Entertaining Mechanics" (dia hanya melihat edisi ke-4 tahun 1937, tetapi tugas itu mungkin pada yang sebelumnya dimulai dari tahun 1930) di bab kesembilan, "Treneye i Resistance " (Ya, awal abad kedua puluh, bagian terakhir) disebut" Kapan hujan akan menjadi lebih baik ? ", Tetapi sebenarnya tugasnya adalah" Dalam hal apa kamu lebih banyak membasahi topimu? ". Ada perbedaan - dalam buku ini kita hanya berbicara tentang komponen hujan yang dilihat topi dari atas, tidak ada pembicaraan tentang tabrakan dengan hujan di bidang vertikal. Selain itu, dalam tugas, percobaan dilakukan pada saat yang sama, di tengah hujan, sementara kami tertarik pada jarak yang sama. Tidak ada keraguan tentang keadilan yang diberikan dalam buku keputusan, tetapi nama bagian itu sendiri, dan kesimpulan independen dari para pembaca, dapat mengarah pada kesimpulan yang salah dan penampilan stereotip.

Setelah Perelman ada artikel dalam jurnal ilmiah populer dari zaman dahulu dan tidak demikian , lalu ada vidos, dan sekarang terjemahannya bahkan ada di hub di sini . Artikel lain yang sulit dilewati adalah artikel ahli fisika Italia Franco Bocci tahun 2012 di European Journal of Physics, artikel itu sendiri tidak mungkin dibaca oleh banyak orang, tetapi banyak ditulis di media, misalnya, itu menarik, menurut pendapat saya, . Ada penelitian lain dengan berbagai tingkat keparahan. Ternyata sejarah masalah ini mungkin tidak kalah menarik dari masalah itu sendiri, dan mungkin menjadi subjek dari artikel terpisah.

Pemodelan

Keterbatasan dan Asumsi

Inti dari pemodelan adalah penyederhanaan yang disengaja dan abstraksi persepsi realitas. Model yang disajikan dalam artikel tidak terkecuali. Lebih lanjut dalam teks mungkin ada indikasi bahwa fitur tertentu karena spesifik tugas, fisik, keterbatasan kognitif, serta pembatasan yang berkaitan dengan agama, ras, politik, seksual dan preferensi penulis lainnya adalah asumsi atau pembatasan (dengan kata lain, hal-hal tersebut , yang tidak hanya terlalu malas untuk dilakukan, tetapi juga terlalu malas untuk menjelaskan mengapa saya tidak membuatnya).

Contoh pembatasan dan asumsi: Jumlah tetes dalam sel adalah satu (batas intensitas maksimum), semua tetes adalah ukuran yang sama, diasumsikan bahwa seseorang tidak melambaikan tangan dan kaki saat berjalan dan berlari (area proyeksi frontal dan horizontal selalu sama), air yang diangkat dari sepatu di bagian belakang tidak diperhitungkan, tidak ada angin dalam percobaan, dll.

Ruang dan manusia

Ruang

Model diwakili oleh dua objek, ruang dan manusia.

Ruang ini adalah paralelepiped persegi panjang, dibagi menjadi kubus berukuran 1x1x1 cm.

Lebar ruang sama dengan lebar orang: dalam percobaan, kasus dengan angin dan angin samping tidak dipertimbangkan, oleh karena itu, tidak masuk akal untuk menghitung ruang di luar lebar orang tersebut.

Ketinggian ruang lebih besar dari ketinggian seseorang oleh satu lapisan kubus horizontal - yaitu, satu sentimeter, di lapisan ini tetes mulai dicatat, yang pada saat berikutnya waktu akan jatuh pada seseorang, atau lebih jauh ke ruang yang tidak ditempati oleh seseorang.

Panjang (luas) ruang - harus sama dengan panjang jarak, tetapi ini sangat tidak ekonomis, karena untuk percobaan Anda hanya perlu tahu tentang keadaan ruang di atas seseorang, dan tentang beberapa lapisan di depannya. Oleh karena itu, ruang digunakan secara siklikal dalam proyek, dan panjangnya dipilih sehingga pada saat orang melewatinya sepenuhnya di lapisan vertikal pertama, semua sel diperbarui. Dengan kata lain, tetesan yang muncul di lapisan tepat di belakang punggung orang tersebut harus memiliki cukup waktu untuk jatuh ke tanah, hingga saat orang tersebut kembali mendekati lapisan ini dengan wajahnya. Jadi, dengan pemilihan panjang ruang yang tepat, tetesan segar akan selalu menetes ke tubuh seseorang.

Perlu dicatat bahwa selama percobaan, panjang ruang ditetapkan satu kali, dan kemudian tidak berubah, oleh karena itu, untuk pengaturan awal nilainya panjang, rasio parameter dipilih sehingga dalam semua kasus panjangnya cukup (kecepatan orang maksimum dan tingkat penurunan jatuh minimum).

Ruang untuk eksperimen dapat dibayangkan dengan cara yang berbeda, misalnya, sebagai koridor tertutup, tetapi saya lebih suka membayangkannya sebagai titik cahaya persegi panjang, dari lentera yang bersinar dari satu sisi ke sisi lain, dan yang bergerak bersama orang tersebut. Setiap tetes yang memasuki cahaya di dalam spot direkam. Pendekatan ini memungkinkan kita untuk memisahkan konsep ruang fisik, tak terbatas di mana seseorang berlari dalam hujan dari ruang eksperimen - sebuah kisi tiga dimensi imajiner, keadaan setiap sel yang diperiksa pada setiap saat waktu percobaan. Dalam artikel tersebut, kata "spasi" digunakan dalam arti kedua.

Dalam program ini, ruang diwakili oleh array byte tiga dimensi. Indeks elemen dalam array sesuai dengan koordinat sel dalam ruang (panjang, tinggi, lebar), elemen itu sendiri menggambarkan keadaan. Hanya ada dua keadaan - ada setetes hujan di sel atau sel kosong.

Ruang juga dapat dibayangkan sebagai seperangkat lapisan horisontal yang melaluinya hujan turun, dan sebagai seperangkat lapisan vertikal yang ditemui seseorang saat bergerak. Dalam program ini, ada kelas - pembungkus yang bertanggung jawab atas representasi ini.

Bung

Orang dalam proyek ini hanyalah sebuah kotak persegi panjang. Untuk percobaan, kami terutama tertarik pada proyeksi pada bidang horizontal untuk menghitung tetesan yang jatuh dari atas, dan proyeksi pada bidang vertikal yang tegak lurus dengan arah gerakan, untuk menghitung tetesan yang ditemui seseorang saat bergerak maju. Juga digunakan adalah koordinat yang bertanggung jawab untuk posisinya di ruang angkasa, dan penghitung air yang dikumpulkan di depan dan atas.

Untuk memperkirakan area proyeksi horisontal yang di-google-kan, salah satu referensi pertama adalah beberapa tindakan pengaturan yang menggunakan Kementerian Keadaan Darurat. Di sana, proyeksi horizontal seseorang diwakili oleh elips dengan dimensi aksial 0,5 m (lebar orang di bahu) dan 0,25 m (ketebalan orang). Tampaknya benar, oleh karena itu saya mengambil persegi panjang dari area yang hampir sama (S elips = pi * a * b S = 3,14 * (50/2) * (25/2) ~ 982 sq. Cm, rectangle 48 dengan 20 = 960 sq. Cm ) Seperti ditunjukkan di atas, data ini digunakan, termasuk untuk menentukan lebar dan luas ruang. Saya tidak menemukan definisi proyeksi vertikal seseorang, oleh karena itu, untuk pertumbuhan saya mengambil nilai sedikit kurang dari rata-rata - 160 cm. Dimensi manusia mudah berubah dalam proyek, tetapi percobaan dilakukan hanya pada satu set parameter. Karena pertanyaan ini tampaknya tidak terlalu menarik bagi saya - pertama, tidak mungkin Anda entah bagaimana mempengaruhi parameter ini dalam hujan, dan kedua, mencari tahu tubuh mana yang optimal untuk menjadi basah dalam hujan mungkin terlihat menyinggung seseorang. Saya menghubungkan ini dengan keterbatasan dan asumsi.

Kecepatan manusia: 2.196 km / jam diambil sebagai batas bawah; diambil dari sini, tampaknya data ini digunakan untuk prostetik, batas atas adalah 43,9 km / jam - kecepatan lari tercepat saat ini dicatat .

Tentang hujan

Hujan dalam suatu proyek adalah proses yang terjadi di ruang angkasa, dan yang memiliki karakteristik sendiri: ukuran tetesan, tingkat jatuh, intensitas.

Menurut Wikipedia, diameter tetesan hujan tidak boleh kurang dari 0,5 mm, karena tidak akan lagi hujan, tetapi gerimis, dan tidak lebih dari 6-7 mm, dalam kondisi seperti itu, tetesan pecah menjadi yang lebih kecil.

Sesuai dengan artikel yang sama, kecepatan tetesan bervariasi dari 2 hingga 6 m / s untuk tetesan kecil dan dari 9 hingga 30 m / s untuk tetesan dengan diameter 5 mm. Dengan ukuran 5mm sampai 7mm, tingkat penurunan menurun karena fakta bahwa tetes besar tersebut berbentuk parasut, dan resistensi udara meningkat. Laju penurunan tetesan tidak hanya tergantung pada ukuran tetesan itu sendiri, tetapi juga pada kondisi penurunannya - saya berasumsi bahwa itu tergantung pada kepadatan udara, keberadaan aliran naik atau turun, dll.

Proyek ini menetapkan ketergantungan linier dari laju jatuh pada panjang diameter: dalam kisaran diameter 0,5 hingga 5 mm, kecepatan meningkat secara linier dari 2 m / s ke 30 m / s (DropSize * 6.22 - 1.11), dalam kisaran dari 5 mm hingga 7 mm, kecepatan berkurang dari intensitas yang sama ((10 - DropSize) * 6.22 - 1.11), di luar kisaran 0,5 - 7 mm, percobaan tidak dilakukan.

Ketergantungan linear yang digunakan dalam percobaan tidak bertentangan dengan gambaran dunia yang ada, tetapi terbatas, dan karenanya merupakan asumsi. Sebagai contoh, penurunan 5 mm dalam proyek sesuai dengan kecepatan 30 m / s - di dunia nyata ini mungkin (menurut Wikipedia), tetapi di dunia nyata juga mungkin bahwa penurunan dengan diameter 5 mm akan jatuh lebih lambat - pada kecepatan 9 m / s . Jika seseorang tertarik dan memutuskan untuk bereksperimen sendiri, maka Anda dapat mengubah ketergantungan ke yang lain, atau bahkan bereksperimen dengan beberapa. Dalam proyek ini, fitur ini akan digunakan dalam jumlah yang sangat terbatas (karena kurangnya waktu).

Intensitas adalah karakteristik hujan yang menarik dan penting. Intensitas biasanya ditunjukkan dalam milimeter per jam. Satu milimeter per jam berarti bahwa dalam satu jam satu lapisan air setebal satu milimeter akan jatuh pada permukaan horizontal satu meter persegi. Tidak sulit untuk menghitung bahwa volume lapisan air ini adalah satu liter. Artinya, satu mm / jam sama dengan satu liter per meter persegi dalam satu jam. Terkadang dalam prakiraan cuaca, ketika mereka ingin menggambarkan skala bencana, mereka hanya menunjukkan milimeter - ini adalah ketinggian dihitung dari lapisan air yang telah jatuh selama seluruh durasi hujan. Dalam proyek ini, dan selanjutnya dalam artikel ini, unit pengukuran akan digunakan - milimeter per jam.

Menurut Wikipedia, intensitas hujan biasanya dari 0,25 mm / jam (hujan gerimis) hingga 100 mm / jam (hujan) - percobaan dilakukan dalam nilai-nilai ini.

Tentang distribusi tetes di ruang:

Ada satu hal menarik yang ingin saya hentikan sebentar. Pada tahap desain, direncanakan bahwa lapisan horizontal atas akan diisi dengan tetesan sebagai berikut: setelah probabilitas tetesan yang muncul dalam sel dihitung, dan kemudian, menyortir semua sel lapisan, pengacak, berdasarkan probabilitas ini, akan menempatkan setetes dalam sel atau tidak. Probabilitas dihitung sebagai rasio jumlah tetes yang diperlukan dalam lapisan terhadap jumlah total sel dalam lapisan. Mengingat kenyataan bahwa ruang sudah dikurangi seminimal mungkin, pendekatan semacam itu tampaknya cukup masuk akal. Namun, sebelum memulai percobaan, saya memutuskan untuk memperkirakan jumlah tetes per unit ruang (probabilitas kejadian yang sama) dan inilah yang terjadi: Di ​​bawah ini adalah grafik jumlah tetes dalam lapisan dengan luas satu meter persegi dan ketebalan satu sentimeter, tergantung pada ukuran tetes, setiap grafik sesuai dengan intensitasnya:

Pada sumbu horizontal - ukuran drop, pada sumbu vertikal - jumlah drop. Sumbu vertikal adalah logaritmik, karena penyebaran dalam jumlah tetes sangat besar. Seperti sebaran besar dijelaskan oleh fakta bahwa volume tetesan sebanding dengan derajat ketiga dimensi liniernya (diameter), ditambah dengan peningkatan ukuran tetesan, laju penurunannya meningkat. Dengan demikian, dengan perubahan kecil dalam diameter tetesan, jumlah tetes dalam volume berubah sangat banyak (misalnya, untuk intensitas hujan 80 mm / jam, dengan diameter tetesan 0,8 mm, diperlukan sekitar 215 tetes per lapisan, dan ketika diameter tetesan digandakan, hingga 1,6 mm, total 12 tetes per lapisan).

Sekarang, berkenaan dengan optimasi: seperti yang dapat dilihat dari grafik, bahkan dengan volume penurunan minimum dan intensitas maksimum, jumlah tetes per 10 ribu sel tidak melebihi 2 x ribu, dalam banyak kasus jumlah tetes kurang dari 100, dan jika diameter drop lebih dari 3 mm, jumlah tetes per lapisan kurang dari satu. Oleh karena itu, iterasi setiap sel pada layer, sehingga akhirnya hanya satu tetes yang muncul di dalamnya tidak ekonomis. Opsi yang lebih ekonomis adalah menghitung jumlah tetes dalam lapisan, dan kemudian secara acak menyebarkannya ke seluruh lapisan. Satu-satunya komplikasi adalah kasus ketika sel yang dipilih sudah penuh (dalam situasi ini, rekursi terlihat bagus). Jika kita menambahkan semua penghafalan sel yang terisi, untuk pembersihan lapisan selanjutnya, maka kita bisa mendapatkan penghematan yang signifikan pada CPU, dengan sedikit peningkatan dalam penggunaan RAM.

Proses emulasi hujan

Proses pemodelan berlangsung dalam satu siklus utama. Setiap iterasi dari siklus ini sesuai dengan interval waktu minimum (centang). Setiap kondisi centang sistem diperbarui dan diperbaiki. Durasi kutu sesuai dengan durasi bagian rintik hujan melalui satu lapisan ruang (dalam kasus kami 1 cm), oleh karena itu satu kutu dalam program dapat sesuai dengan interval waktu yang berbeda dalam kehidupan nyata, tergantung pada parameter input (atau lebih tepatnya, pada kecepatan tetesan jatuh). Berikut ini menjelaskan tindakan yang terjadi dalam setiap iterasi:

Proses hujan dalam proyek adalah sebagai berikut: pertama, lapisan atas diisi secara acak dengan tetesan (lihat bagian di atas), biarlah itu menjadi nomor lapisan n. Dalam iterasi berikutnya, jatuh dari lapisan ke-n jatuh ke dalam sel-sel dari lapisan yang terletak tepat di bawahnya - ke dalam nomor lapisan n-1, lapisan atas diisi lagi. Selanjutnya, semuanya terjadi dengan cara yang sama: tetes-tetes lapisan n-1 jatuh ke lapisan n-2, tetes-tetes ke-n ke dalam lapisan n-1, dan tetes-ke-n lagi secara acak, dan seterusnya. Ketika tetesan mencapai lapisan terendah, mereka tidak gagal di mana pun, tetapi menghilang begitu saja (katakanlah, jatuh ke tanah, dan diserap), dan kemudian, setelah dibersihkan, lapisan ini naik dan digunakan kembali.

( ) , . , , ( ). . , , , , , ( ) , , .

, , ( ), , , , .

( ), ( ). , . , , . , . — , . , , , , . , , .

, , . , , , .

, , , .

, .

, – « , , , ?» – « ?»

. «», , , , : , ?

. « ?»

. « – , ? ?»

, . : , , , . 1 , .

, , . 2,2 /, 23,04 /, , 43,88 /. . – , .

, , . – , , , . , . , . , , . : (0.6 ), (7 ), 5 () «» (1.4 ). 10 (10 – 100 /). 1, 50 100 (, , ). . , , .

:

Hasil dan Kesimpulan

, . , , 12 , 36 1 . 32 529 927 , 2 . , , , .

. , . , : « ?» : . .

, , « , ?» — , , - . :

( 20 /) 1 , 3.2 ~ 26% . , : 0,0005841873 1 1712 , 1 7,06 . – , , , , , . .

20 100 , . 23 / 43 /. , , « , ». : , , , .

, « ?».

, , :

0.6 5 , , 5 – 7 ( 7 , 5). , , .

, – , . , ( ), : , , .

– , .

, 50/ ( ). , :

, , , , .

- , . , . , , , , , , .

: « – , ? ?».

, , , , .

, :

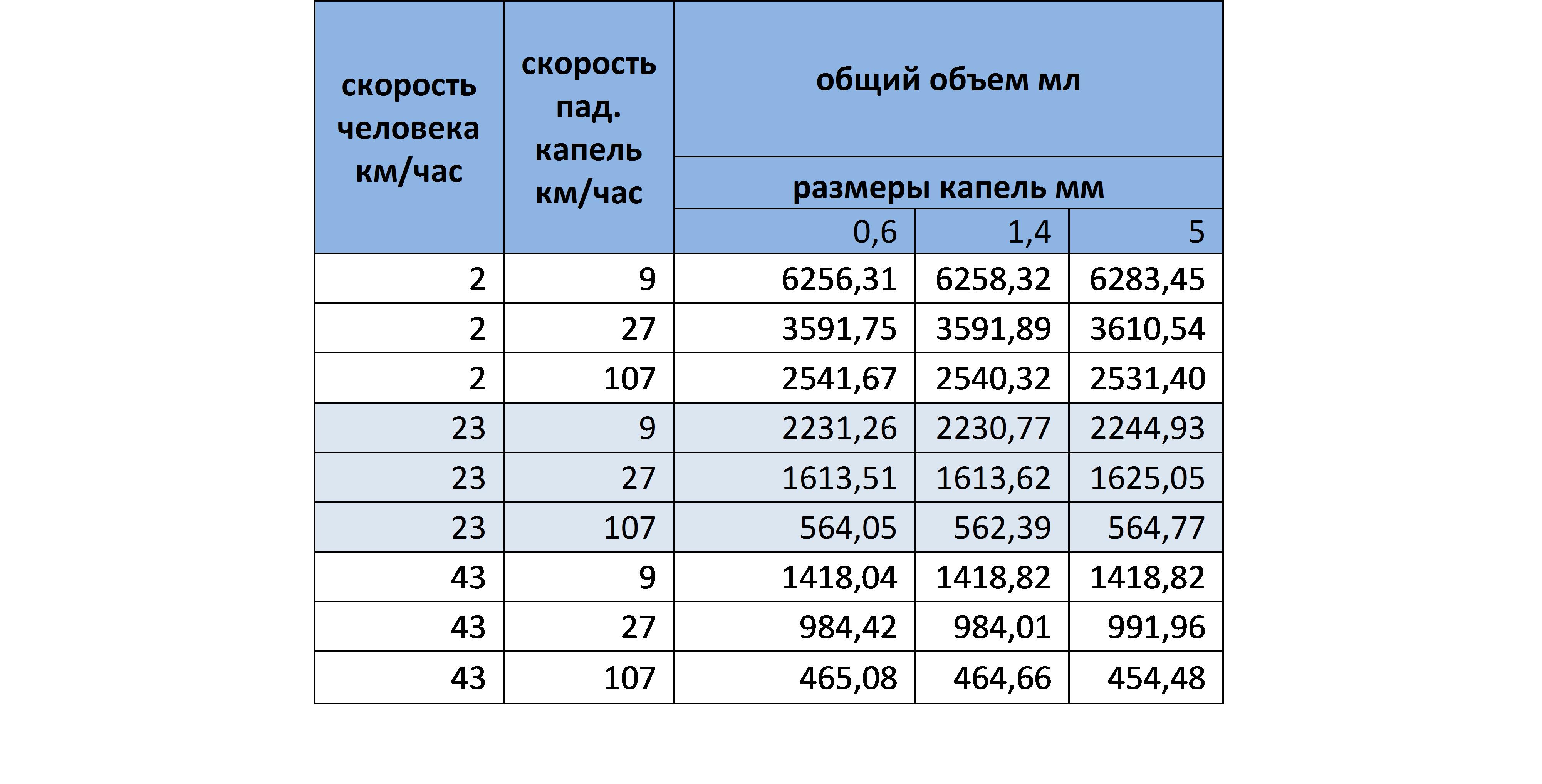
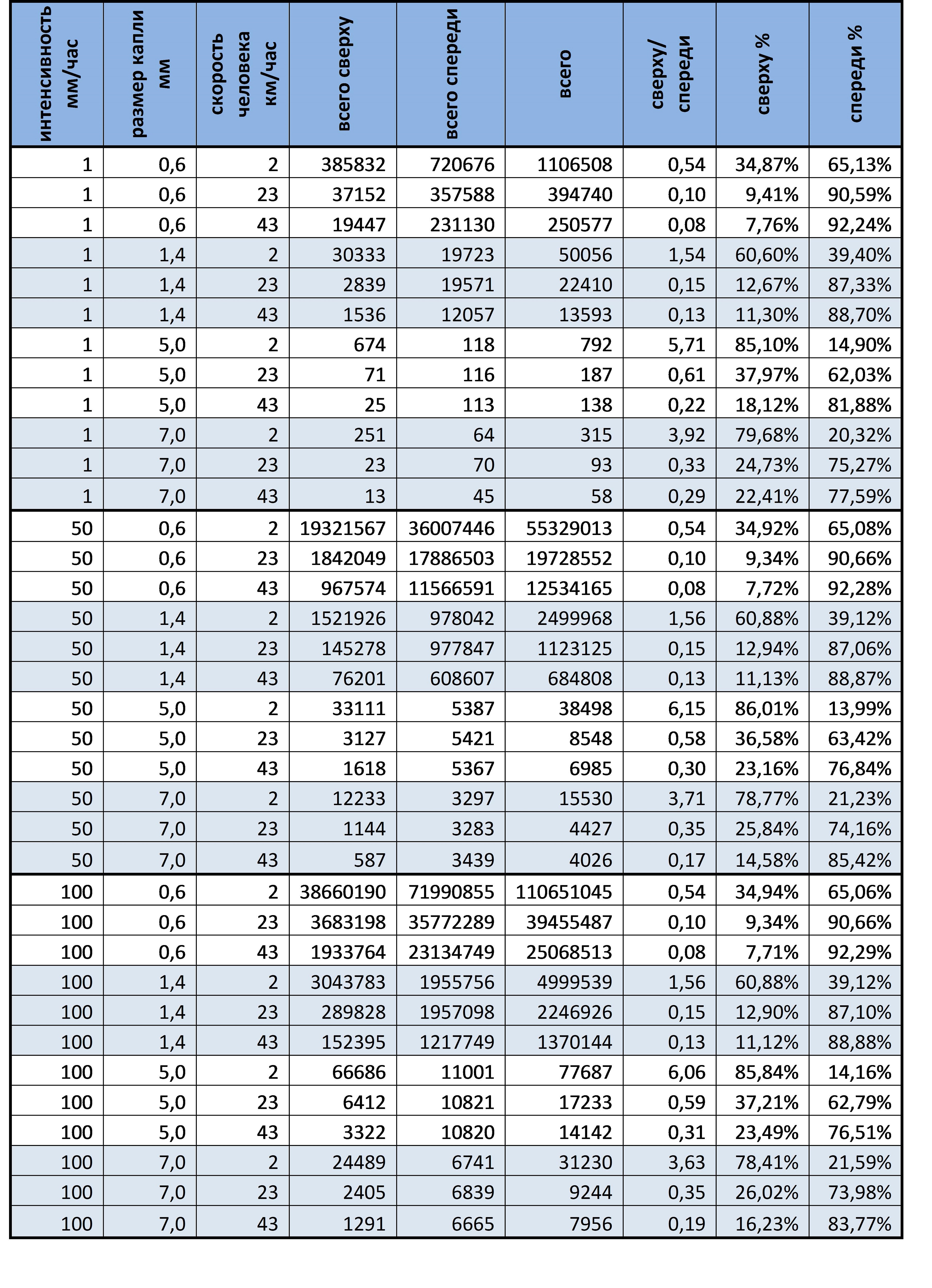
1) – , ( ).

2) , , ( 2 / 50 %).

3) , , , , ( ).

4) , . , ( ):

Ini berarti bahwa semakin besar tingkat jatuh, semakin kuat Katya dapat memengaruhi volume akhir air yang terkumpul. Dengan kata lain, jika Anda terjebak dalam hujan lebat yang mencambuk tetes besar, semakin cepat Anda lari ke tempat perlindungan, semakin sedikit Anda basah. Dan sebaliknya, jika ada gerimis di jalan, banyak tetesan kecil menggantung di udara, maka tidak ada gunanya berlari, ini tidak akan sangat mempengaruhi hasil akhir.

Dengan demikian, jawaban untuk pertanyaan keempat adalah "Di sisi mana seseorang akan mengumpulkan lebih banyak air - dari atas atau dari depan?" Rasio ini tergantung pada apa? ”Bunyinya: Seseorang yang berjalan di tengah hujan dapat mengumpulkan lebih banyak air dari atas dan dari depan, rasio ini terutama tergantung pada kecepatannya, tetapi tingkat penurunan jatuh memiliki pengaruh yang besar. Semakin besar kecepatan seseorang, semakin sedikit tetes yang akan menimpanya dari atas.

Itu mungkin saja. Scott, seorang ahli paleontologi, mengatakan, mempelajari alam dan membuat penemuan Anda sendiri, kawan. :)

PS Mungkin ada kesalahan dalam teks, dalam model, dalam hasil, dalam pertanyaan yang diajukan dan jawaban kepada mereka, dan di tempat lain, jadi saya memposting proyek di domain publik jika seseorang ingin memeriksa, memeriksa ulang, mengulang, menambah, menyangkal, menyodok, menyodok nose, dll. - menyambut Anda github.com/sv-kopylov/raindrops-pub.git .

PPS Artikel ini adalah kelanjutan, sekarang serangkaian artikel tentang menghibur pemodelan komputer, artikel pertama di sini.