n-Queens Completion Problem - algoritma solusi linier

Ericgrig

Kata Pengantar

Saya ingin memulai kata pengantar dengan kata-kata terima kasih kepada dua programmer yang hebat dari Odessa: Andrei Kiper (Lohica) dan Timur Giorgadze (Luxoft), untuk verifikasi independen atas hasil saya, pada tahap awal penelitian.

1. Artikel "Algoritma linear untuk solusi n-Queens Completion Problem" diterbitkan di (arXiv.org) pada awal hari pertama tahun 2020. Awalnya, artikel itu ditulis dalam bahasa Rusia, jadi presentasi dasar disajikan di sini, dan ada terjemahannya.
2. Tugas ini, dan beberapa lainnya dari banyak set NP-Complete (tugas memuaskan formula Boolean (3-SAT), tugas untuk menemukan klik maksimum, atau klik dengan ukuran tertentu ...) pada waktu yang berbeda, berada dalam bidang yang saya minati. Saya sedang mencari solusi algoritmik berdasarkan berbagai eksperimen komputasi, tetapi tidak ada keberhasilan konkret. Itu seperti seseorang yang mencoba belajar bagaimana menjadi bugar di bar horizontal dengan satu tangan. Tidak ada hasil, tetapi setiap kali ada harapan bahwa semuanya akan segera berhasil. Terakhir kali saya memutuskan bahwa saya harus tinggal lebih lama pada tugas Penyelesaian n-Queens (sebagai salah satu anggota keluarga) dan mencoba melakukan sesuatu. Di sini tepat untuk mengingat lelucon Odessa yang indah: "Di dalam bus yang penuh sesak yang kembali ke pinggiran kota di jalan bergelombang di malam hari, suara seorang wanita terdengar - Pria, jika Anda benar-benar memakainya, lakukan setidaknya sesuatu."
3. Penelitian ini berlangsung cukup lama - hampir satu setengah tahun. Di satu sisi, ini disebabkan oleh kenyataan bahwa tugas-tugas lain dipertimbangkan dalam proses penelitian, dan di sisi lain, ada pertanyaan-pertanyaan sulit di sepanjang jalan, yang tanpanya kami tidak bisa maju. Saya akan membuat daftar beberapa di antaranya:
   
   
   • Ada n baris dalam matriks keputusan, dalam urutan apa indeks baris harus dipilih jika jumlah kemungkinan untuk pilihan seperti itu adalah n!
   • ketika sebuah baris dibuat, yang mana dari posisi bebas yang tersisa di baris ini harus dipilih, karena jumlah kemungkinan untuk seleksi sedemikian besar sehingga dapat dianggap sebagai "kerabat dekat" tanpa batas (misalnya, jumlah cara yang mungkin untuk memilih posisi bebas di semua baris untuk papan catur ukuran 100) x 100 adalah sekitar 10 ¹²⁴ )
   • Bersama-sama, kedua indikator ini membentuk ruang negara (ruang pilihan). Tampaknya ada peluang besar, Anda dapat memilih apa yang Anda inginkan. Namun di balik setiap pilihan spesifik pada setiap langkah, ada masalah lain - keterbatasan pilihan dalam semua langkah selanjutnya. Selain itu, ini sangat sensitif pada tahap terakhir dari penyelesaian masalah. Kita dapat mengatakan bahwa matriks keputusan itu "pendendam." Semua "kesalahan tak sadar" yang Anda buat ketika membuat pilihan pada tahap sebelumnya adalah "terakumulasi", dan pada akhir keputusan ini dimanifestasikan dalam kenyataan bahwa di baris di mana Anda harus meletakkan ratu, tidak ada posisi kosong dan cabang pencarian terhenti. . Di sini, seperti halnya Zhvanetsky: "satu langkah yang salah, dan Anda hamil."
   • Ketika cabang pencarian solusi terhenti, kami memiliki kesempatan untuk kembali ke beberapa posisi sebelumnya (Back Tracking), sehingga dari posisi ini kami akan kembali membentuk cabang pencarian untuk solusi. Ini adalah "properti" alami dari masalah non-deterministik. Pertanyaannya adalah level mana yang sebelumnya harus dikembalikan. Ini adalah masalah terbuka yang sama dengan pertanyaan memilih indeks baris, atau memilih posisi bebas di baris ini.
   • Akhirnya, masalah yang berkaitan dengan kecepatan algoritma harus diperhatikan. Alangkah menyedihkan jika tidak ada tujuan untuk membuat algoritma yang berjalan cepat. Dalam proses pemodelan, tidak mungkin untuk mengembangkan satu algoritma yang akan bekerja dengan cepat dan efisien di semua bidang solusi masalah. Saya harus mengembangkan tiga algoritma. Mereka mengirimkan hasil satu sama lain, seperti tongkat. Salah satunya bekerja sangat cepat, tetapi kasar, yang lain - sebaliknya, bekerja perlahan tapi efisien. Masing-masing dari mereka bekerja di "zona tanggung jawab mereka".
4. Awalnya, tujuan dari penelitian ini hanya untuk menemukan setidaknya beberapa solusi. Saya harus mencari tahu sebelum solusi pertama dikembangkan. Butuh lebih dari empat bulan. Itu mungkin untuk berhenti di sana, tujuannya tercapai - yah, oke. Tetapi bagi saya tampaknya tidak semua kemungkinan solusi algoritmik untuk masalah ini telah habis. Secara alami, ada keinginan untuk meningkatkan algoritma yang dikembangkan sehingga kompleksitas waktu dari algoritma itu linier-O (n). Ketika solusi linear ditemukan, ada "satu keinginan lagi" - untuk mengurangi jumlah kasus ketika prosedur Pelacakan Kembali (BT) diterapkan ketika membentuk cabang pencarian solusi. Itu adalah keinginan "kurang ajar" untuk mengalihkan tugas dari tidak deterministik ke ditentukan secara kondisional (sejauh mungkin). Butuh banyak waktu, tetapi tujuannya tercapai, misalnya, dalam interval nilai ukuran papan catur n = (320, ..., 22500), jumlah kasus ketika prosedur BT tidak pernah digunakan lebih dari 50%. Ternyata dalam 50% kasus ketika program diluncurkan, algoritma "sengaja" membentuk solusi, tidak pernah "tersandung". (Mengingat dongeng tentang ikan mas, aku berhenti pada dua keinginan ini ...)
5. Membandingkan publikasi yang berhasil saya kenali selama penelitian, saya sampai pada kesimpulan bahwa masalah ini dan masalah lain semacam ini tidak dapat diselesaikan berdasarkan pendekatan matematika yang ketat, yaitu, hanya berdasarkan definisi, pernyataan lemmas dan bukti teorema. Ada "pernyataan filosofis" tentang ini dalam artikel ini. Saya yakin bahwa banyak masalah dari banyak NP-Complete dapat diselesaikan hanya berdasarkan matematika algoritmik dengan menggunakan pemodelan komputer. Kesimpulan seperti itu tidak berarti membatasi matematika, sebaliknya, itu berarti memperluas kemampuan matematika melalui pengembangan metode matematika algoritmik. Untuk setiap keluarga masalah Anda perlu menggunakan pendekatan matematika Anda sendiri yang memadai. (Mengapa menugaskan mahasiswa pascasarjana untuk menyelesaikan masalah dari keluarga NP-Complete tanpa menerapkan matematika algoritmik dan metode pemodelan komputer, jika diketahui bahwa tidak ada yang benar-benar akan datang dari usaha semacam itu).
6. Algoritma apa saja (program) memiliki properti sederhana - baik itu berfungsi atau tidak! Saya ingin menarik bagi anggota Komunitas Habro kami yang memiliki komputer dengan Matlab diinstal di zona aksesibilitas. Saya ingin meminta Anda untuk menguji operasi algoritma yang dipertimbangkan untuk menyelesaikan Masalah Penyelesaian n-Queens . Ini akan memakan waktu hanya 5-10 menit. Untuk menguji algoritme, Anda perlu mengikuti beberapa langkah sederhana:
   
   
   • Hasilkan komposisi acak dari k queens dan periksa kebenaran komposisi ini.
   • Berdasarkan algoritma keputusan yang diusulkan, isi komposisi ini hingga solusi lengkap. Atau program harus memutuskan bahwa komposisi ini tidak memiliki solusi.
   • Periksa kebenaran solusi yang diperoleh sebagai hasil dari konfigurasi.
   
   
   Anda tidak harus menulis kode apa pun untuk pengujian semacam itu. Selain program utama, saya menyiapkan dua program lagi dalam bahasa Matlab:
   
   1. Generarion_k_Queens_Composition - pembuatan komposisi acak ukuran k untuk papan catur acak berukuran nxn
   
   2. Completion_k_Queens_Composition.m - menyelesaikan komposisi sewenang-wenang hingga keputusan lengkap, atau memutuskan bahwa komposisi ini tidak memiliki solusi ( program utama ).
   
   3. Validation_n_Queens_Solution.m - memeriksa kebenaran solusi dari Masalah n-Queens , atau kebenaran komposisi k queens.
   
   Mereka bekerja sangat cepat. Misalnya, untuk papan catur, yang ukurannya 1000 x 1000 sel, total waktu yang dibutuhkan rata-rata untuk menghasilkan komposisi sewenang-wenang (0,0015 dt.), Lengkapi komposisi ini (0,0622 dt.), Dan verifikasi kebenaran solusi yang diperoleh (0,0003 dt.) tidak melebihi 0,1 detik. (tidak termasuk waktu yang diperlukan untuk mengunduh data, atau menyimpan hasilnya)
   
   Email saya (ericgrig@gmail.com), jika Anda memiliki kesempatan untuk membantu teman, saya akan segera mengirimkan kepada Anda tiga program ini. Saya akan berterima kasih kepada semua kolega saya yang secara objektif dapat menguji algoritma dan mengungkapkan pendapat mereka dalam diskusi.
7. Saya menyiapkan kode sumber program, dengan komentar terperinci, yang, saya harap, akan segera diterbitkan di Habré. Saya pikir mereka yang tertarik untuk menyelesaikan masalah kompleks dari keluarga NP-Complete akan menemukan sesuatu yang menarik untuk diri mereka sendiri.
8. Saya ingin memohon lagi kepada anggota Komunitas Habr, tetapi untuk alasan yang berbeda. Di sini, di Marseilles (Prancis), pembentukan tim Grup Perancis Lipat sedang berlangsung, yang tujuannya adalah untuk meneliti dan mengembangkan algoritma untuk memprediksi sifat fisikokimia senyawa berat molekul tinggi. Saya pikir itu tidak layak untuk mengatakan bahwa ini adalah tugas yang agak sulit, dengan sejarah yang panjang, dan bahwa tim serius di berbagai negara sedang mengerjakan masalah ini, termasuk tim Khasabis dari Deep Mind (Anda dapat melihat artikel tentang Habré (habr.com_Folding) . Tujuannya adalah untuk menciptakan tim yang kuat yang tidak takut untuk menyelesaikan masalah yang kompleks. Bentuk organisasi kerja bersama didistribusikan. Setiap anggota tim tinggal di kotanya dan bekerja pada proyek di waktu luangnya dari pekerjaan utamanya. Kita membutuhkan programmer dan peneliti (fisikawan, kimiawan, ahli matematika, ahli biologi) ), dll. osto "sembrono" programmer- (kuadrat). Tuliskan saya jika Anda merasa menarik, di atas adalah email saya. Secara lebih rinci saya bisa kirim dalam surat tanggapan.

Kata pengantar untuk artikel itu ternyata sepanjang artikel itu sendiri. Format presentasi keluarga tentang Habré memungkinkan saya untuk mengekspresikan pikiran saya lebih bebas, tetapi menilai dari ukurannya, saya memanfaatkannya dengan cukup bebas. Saya ingin menulis sebentar, tetapi "ternyata seperti biasa."

PS Saya berpikir bahwa anggota Komunitas Habr akan tertarik untuk mengetahui kesulitan apa yang saya temui ketika mencoba untuk mempublikasikan hasil penelitian. Ketika artikel itu disiapkan, saya memformatnya ke dalam format .tex sesuai dengan persyaratan Journal of Artificial Intelligence Research (JAIR) dan mengirimkannya ke sana. Dulu ada publikasi tentang topik serupa. Dari catatan khusus adalah artikel C. Gent, I.-P. Jefferson dan P. Nightingale (2017) (Kompleksitas penyelesaian n-queens) , di mana penulis membuktikan bahwa masalah tersebut adalah milik set NP-Complete dan berbicara tentang kesulitan yang dihadapi dalam mencoba menyelesaikan masalah ini. Dalam kesimpulan, penulis menulis: "Bagi siapa pun yang memahami aturan catur, n-Queens Completion mungkin menjadi salah satu masalah NP-Complete paling alami dari semua" ( Untuk semua orang yang memahami aturan catur, tugas Penyelesaian n-Queens dapat menjadi salah satu dari tugas NP-Complete paling alami ).

Setelah 10 hari, saya menerima penolakan dari JAIR, dengan kata-kata: "artikel itu tidak sesuai dengan format jurnal", yaitu bahkan tidak mengambil artikel untuk dipertimbangkan. Saya tidak mengharapkan jawaban seperti itu. Saya berpikir bahwa jika jurnal menerbitkan artikel yang penulis simpulkan bahwa sangat sulit untuk menyelesaikan masalah yang diberikan dan tidak memberikan solusi konkret, maka artikel yang menyediakan algoritma solusi yang efektif tentu akan diterima untuk dipertimbangkan. Namun, redaksi memiliki pendapat sendiri tentang hal ini. (Saya percaya bahwa spesialis yang kompeten bekerja di sana, dan kemungkinan besar mereka ditanyai dengan judul artikel “kurang ajar” dan segala sesuatu yang dinyatakan di sana. Kami berpikir, “kemungkinan besar ada semacam kesalahan dan dengan lembut mengirim saya pergi, merujuk pada format ").

Saya harus memilih publikasi ilmiah berkala peer-review lain tentang topik yang relevan. Di sini saya dihadapkan dengan kenyataan pahit. Faktanya adalah bahwa sekitar 80% dari semua majalah dibayar: baik saya harus membayar jumlah yang layak ke majalah sehingga artikel tersedia secara bebas untuk semua pembaca, atau mereka perlu memberikan artikel sebagai hadiah "di haluan", dan mereka akan membebankan biaya kepada semua orang yang ingin berkenalan dengan penelitian ini. Dan opsi pertama dan kedua secara fundamental tidak dapat saya terima. Saya merasa senang dengan metode raket penerbit ini ketika saya mencoba membiasakan diri dengan beberapa publikasi.

Majalah berikutnya, yang menganut prinsip akses gratis ke informasi, adalah SMAI Journal of Computational Mathematics . Mereka juga menolak dengan kata-kata yang sama, meskipun jauh lebih cepat - dalam dua hari.

Kemudian sebuah jurnal dipilih: Discrete Mathematics & Theoretical Computer Science . Di sini persyaratannya sederhana, pertama Anda perlu menerbitkan artikel di arXiv.org, dan hanya setelah itu daftarkan artikel untuk dipertimbangkan. Oke, kami akan mengikuti aturan - saya mengirimkan artikel di arXiv.org . Mereka menulis kepada saya bahwa mereka akan menerbitkan artikel dalam 8 jam. Namun, ini tidak terjadi setelah 8 jam, tidak setelah 8 hari. Artikel itu "dipegang" oleh para mentor, dan hanya setelah 9 hari diterbitkan. Tidak ada keluhan dalam bentuk dan esensi artikel. Saya pikir, seperti dalam kasus JAIR, mentor memiliki keraguan tentang kemungkinan "melakukan ini dan menulis tentang itu." Beberapa waktu kemudian, setelah memperbaiki kesalahan teknis, artikel itu diperbarui dan dalam bentuk akhirnya dirilis pada malam Tahun Baru.

Saya harus membahas hal ini secara rinci untuk menunjukkan bahwa pada tahap publikasi hasil penelitian mungkin ada masalah yang tidak dapat dijelaskan secara logis.

Berikut ini adalah artikel yang terjemahannya ke dalam bahasa Inggris diterbitkan di (arXiv.org) .

1. Pendahuluan

Di antara berbagai opsi untuk merumuskan masalah n-Queens, tugas Penyelesaian n-Queens yang bersangkutan memiliki posisi khusus karena kerumitannya. Dalam karya mereka (Gent at all (2017)) menunjukkan bahwa masalah Penyelesaian n-Queens milik set NP-Complete ( menunjukkan bahwa Penyelesaian n-Queens adalah NP-Complete dan # P-Complete ). Diasumsikan bahwa solusi untuk masalah ini dapat membuka jalan bagi kita untuk menyelesaikan beberapa masalah lain dari set NP-Complete .

Masalahnya dirumuskan sebagai berikut. Ada komposisi k ratu, yang secara konsisten didistribusikan di papan catur berukuran nxn . Diperlukan untuk membuktikan bahwa komposisi ini dapat diselesaikan untuk solusi yang lengkap, dan memberikan setidaknya satu solusi, atau untuk membuktikan bahwa solusi seperti itu tidak ada. Di sini, dengan konsistensi, yang kami maksud adalah komposisi k ratu yang memenuhi tiga kondisi masalah: di setiap baris, setiap kolom, dan juga diagonal kiri dan kanan melewati sel tempat ratu berada, tidak lebih dari satu ratu berada. Masalah dalam bentuk ini pertama kali dirumuskan oleh Nauk (1850) .

1.1 Definisi

Selanjutnya, kita akan menunjukkan ukuran sisi papan catur dengan simbol n . Sebuah solusi akan disebut lengkap jika semua n queens secara konsisten ditempatkan di papan catur. Semua solusi lain, ketika jumlah k ratu yang ditempatkan dengan benar kurang dari n - kami akan memanggil komposisi. Kami menyebut komposisi k ratu positif jika dapat diselesaikan sebelum solusi lengkap. Karenanya, komposisi yang tidak dapat diselesaikan hingga solusi lengkap disebut negatif. Sebagai analog dari "papan catur" ukuran nxn , kami juga akan mempertimbangkan "matriks solusi" ukuran nxn . Sebagai contoh, semua algoritma yang dikembangkan untuk memecahkan masalah akan disajikan dalam bahasa Matlab.

Penelitian dilakukan berdasarkan simulasi komputer (simulasi komputasi). Untuk menguji hipotesis ini atau itu, kami melakukan eksperimen komputasi dalam berbagai nilai n = (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 500, 800, 800, 1000, 3000, 3000, 5000, 10.000, 30.000, 50.000, 80.000, 10 ⁵ , 3 * 10 ⁵ , 5 * 10 ⁵ , 10 ⁶ , 3 * 10 ⁶ , 5 * 10 ⁶ , 10 ⁷ , 3 * 10 ⁷ , 5 * 10 ⁷ , 8 * 10 ⁷ , 10 ⁸ ) dan, tergantung pada nilai n , sampel yang cukup besar dihasilkan untuk analisis. Kami menyebut daftar tersebut sebagai " daftar dasar nilai n " untuk melakukan eksperimen komputasi. Semua perhitungan dilakukan pada komputer biasa. Pada saat perakitan (awal 2013), itu adalah konfigurasi yang cukup sukses: CPU - Intel Core i7-3820, 3,60 GH, RAM-32,0 GB, GPU-NVIDIA Ge Forse GTX 550 Ti, perangkat disk- ATA Intel SSD, SCSI, OS- Sistem Operasi 64-bit Windows 7 Professional . Kami menyebut kit ini secara sederhana - desktop-13 .

2. Persiapan data

Algoritme dimulai dengan membaca file yang berisi array data satu dimensi tentang distribusi komposisi sewenang-wenang dari k queens. Diasumsikan bahwa data disusun dengan cara berikut. Biarkan ada array yang memusatkan perhatian Q (i) = 0, i = (1, ..., n) , di mana indeks sel-sel array ini sesuai dengan indeks baris matriks solusi. Jika dalam beberapa baris arbitrer i dari matriks solusi ada ratu di posisi j , maka tugas Q (i) = j dilakukan. Dengan demikian, ukuran komposisi k , akan sama dengan jumlah sel bukan nol dari array Q. (Misalnya, Q = (0, 0, 5, 0, 4, 0, 0, 3, 0, 0) berarti bahwa kami mempertimbangkan komposisi k = 3 ratu pada matriks n = 10 , di mana ratu terletak di ke-3, Baris ke-5 dan ke-8, masing-masing di posisi: 5, 4, 3).

3. Algoritma untuk memverifikasi kebenaran solusi masalah n-Queens

Untuk penelitian, kami membutuhkan algoritma yang akan memungkinkan kami untuk menentukan kebenaran solusi dari masalah n-Queens dalam waktu singkat. Mengontrol lokasi ratu di setiap baris dan setiap kolom sederhana. Pertanyaannya adalah tentang batas diagonal. Kita dapat membangun algoritma yang efektif untuk penghitungan seperti itu jika kita dapat memetakan setiap sel dari matriks solusi ke sel tertentu dari vektor kontrol tertentu yang akan secara unik mengkarakterisasi pengaruh pembatasan diagonal pada sel yang dimaksud. Kemudian, berdasarkan apakah sel vektor kontrol bebas atau sibuk, kita dapat menilai apakah sel yang sesuai dari matriks keputusan bebas atau tertutup.Gagasan seperti itu pertama kali digunakan oleh Sosic & Gu (1990) untuk memperhitungkan dan mengakumulasikan sejumlah situasi konflik antara berbagai posisi ratu. Kami menggunakan ide serupa dalam algoritme yang disajikan di bawah ini, tetapi hanya untuk memperhitungkan apakah sel matriks solusi bebas atau sibuk. Gambar 1, sebagai contoh, menunjukkan papan catur 8 x 8 di atas yang urutan 24 sel terletak di atas .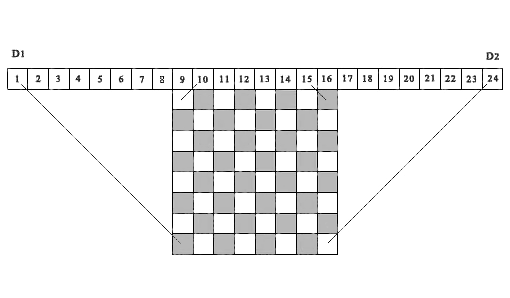


Fig. 1. Contoh demo dari korespondensi proyeksi diagonal dari sel-sel matriks ke sel-sel yang sesuai dari array kontrol D1 dan D2 , ( n = 8)

Pertimbangkan 15 sel pertama sebagai elemen dari vektor kontrol D1. Proyeksi semua diagonal kiri dari sel mana pun dari matriks solusi jatuh ke dalam salah satu sel dari vektor kontrol D1 . Faktanya, semua proyeksi seperti itu terletak di dalam dua segmen garis paralel, yang satu menghubungkan sel dari matriks (8.1) dengan sel pertama dari vektor D1 , dan yang kedua - sel dari matriks (1.8) dengan sel ke 15 dari vektor kontrol D1 . Kami memberikan definisi yang sama untuk proyeksi diagonal kanan. Untuk melakukan ini, pindahkan titik asal dari sel 1 ke sel 9 ke kanan, dan pertimbangkan urutan 16 sel sebagai elemen dari vektor kontrol D2(dalam gambar, ini adalah sel dari 9 ke 24). Proyeksi semua diagonal kanan dari sel mana pun dari matriks solusi akan jatuh ke salah satu sel dari vektor kontrol ini, mulai dari sel ke-2 hingga ke-16 (dalam gambar, dari 10 24). Di sini, semua proyeksi seperti itu terletak di antara dua segmen garis paralel - segmen yang menghubungkan sel (8,8) dari matriks solusi dengan sel 16 dari vektor D2 (sel 24 pada gambar) dan segmen yang menghubungkan sel (1,1) dari matriks solusi dengan sel 2 dari vektor kontrol D2 (sel 10 pada gambar). Proyeksi semua sel dari matriks solusi terletak pada jatuh diagonal kiri yang sama ke dalam sel yang sama dari vektor kontrol D1, masing-masing, proyeksi semua sel dari matriks solusi yang terletak pada diagonal kanan yang sama jatuh ke dalam sel yang sama dari vektor kontrol kanan D2 . Dengan demikian, dua vektor kontrol ini D1 dan D2 , memungkinkan kontrol penuh semua penghambatan diagonal untuk setiap sel dari matriks keputusan.

Penting untuk dicatat bahwa gagasan menggunakan proyeksi diagonal ke sel-sel vektor kontrol untuk menentukan apakah sel matriks solusi dengan koordinat (i, j) bebas atau sibuk juga kemudian diimplementasikan dalam Richards (1997). Ini menyediakan salah satu algoritma pencarian rekursif tercepat untuk semua solusi, berdasarkan operasi dengan sedikit topeng. Perbedaan penting adalah bahwa algoritma yang ditunjukkan dirancang untuk pencarian berurutan dari semua solusi, mulai dari baris pertama dari matriks solusi - turun, atau dari baris terakhir dari matriks - naik. Algoritma yang kami usulkan didasarkan pada kondisi bahwa pilihan jumlah setiap baris untuk lokasi ratu harus sewenang-wenang. Untuk algoritma yang dipertimbangkan, ini sangat penting. Perhatikan bahwa gambar di atas 1, kami membangun dengan analogi dengan apa yang diterbitkan dalam makalah ini.
Suatu program untuk memeriksa apakah solusi yang diberikan dari masalah n-Queens benar, atau apakah komposisi yang diberikan dari k benarRatu adalah sebagai berikut.

1. Untuk mengontrol hambatan diagonal, buat dua array D1 (1: n2) dan D2 (1: n2) , di mana n2 = 2 * n, dan sebuah array B (1: n) untuk mengontrol hunian kolom kolom dari matriks solusi. Hentikan tiga array ini.

2. Kami memperkenalkan penghitung jumlah ratu yang dipasang dengan benar ( totPos = 0 ). Secara konsisten, dalam satu siklus, mulai dari baris pertama, kami mempertimbangkan semua posisi ratu yang disediakan. Jika Q (i)> 0 , maka berdasarkan indeks baris i dan indeks posisi ratu di baris ini j = Q (i), kami membentuk indeks yang sesuai untuk array kontrol D1 (r) dan D2 (t) :
r = n + j - i
t = j + i

3. Jika semua kondisi ( D1 (r) = 0, D2 (t) = 0, B (j) = 0 ) terpenuhi , ini berarti bahwa sel ( i, j) gratis dan tidak termasuk dalam zona proyeksi pembatasan diagonal yang dibentuk oleh ratu yang telah ditetapkan sebelumnya. Posisi ratu dalam posisi ini benar. Jika setidaknya salah satu dari kondisi ini tidak terpenuhi, maka pilihan posisi seperti itu akan salah, masing-masing, dan keputusan akan salah.

4. Jika solusinya benar, maka tambahkan penghitung jumlah ratu yang dipasang dengan benar ( totPos = totPos + 1 ), dan tutup sel yang sesuai dari array kontrol: (D1 (r) = 1, D2 (t) = 1, B (j) = 1) . Jadi kami menutup semua sel di kolom(j) dan sel-sel dari matriks solusi yang terletak di sepanjang diagonal kiri dan kanan berpotongan di dalam sel (i, j) .

5. Ulangi prosedur verifikasi untuk semua posisi yang tersisa.
Mungkin ini adalah salah satu algoritma tercepat untuk mengevaluasi kebenaran solusi untuk masalah n-Queens . Waktu verifikasi satu juta posisi untuk matriks solusi 10 ⁶ x 10 ⁶ pada desktop-13 adalah 0,175 detik, yang kira-kira sama dengan waktu menekan tombol "Enter". Jelas, algoritma ini linier sehubungan dengan penghitungan waktu sehubungan dengan n .

4. Deskripsi algoritma untuk memecahkan masalah

Jenderal . Masalah penyelesaian n-Queens adalah masalah klasik non-deterministik. Kesulitan utama solusinya terkait dengan masalah memilih indeks baris dan indeks posisi di baris ini, dalam kondisi ketika ruang keadaan sangat besar. Saat mencari semua solusi yang mungkin, masalah seperti itu tidak muncul. Kami harus mempertimbangkan semua cabang pencarian yang valid di ruang negara, dan urutan yang dianggap tidak masalah. Namun, ketika komposisi sewenang-wenang dari k ratu perlu diselesaikan sampai solusi lengkap, maka dalam hal ini kita membutuhkan algoritma untuk memilih indeks baris dan kolom yang cukup memahami komposisi yang ada dan mengarah ke solusi lebih cepat daripada yang lain. Dalam proyek ini, kami memutuskan pertanyaan pilihan berdasarkan posisi umum berikut - jika kami tidak dapat merumuskan kondisi yang memberikan preferensi untuk setiap baris atau posisi apa pun di baris ini daripada yang lain, maka kami menggunakan algoritma pemilihan acak berdasarkan nomor acak yang didistribusikan secara merata . Metode seleksi acak serupa untuk memecahkan masalah di mana ruang negara sangat besar adalah sangat alami. Salah satu edisi dari seri Prosiding Workshop DIMACS (1999) sepenuhnya dikhususkan untuk penggunaan seleksi acak dalam pengembangan algoritma untuk memecahkan masalah yang kompleks. Implementasi yang benar dari algoritma pemilihan acak dapat menjadi solusi yang cukup produktif, meskipun ini adalah kondisi yang diperlukan tetapi tidak cukup untuk penyelesaian solusi. Sosic dan Gu (1990) adalah salah satu studi pertama yang menggunakan algoritma pemilihan acak untuk menyelesaikan Masalah n-Queens . Algoritma yang mereka teliti didasarkan pada ide yang cukup sederhana dan ringkas. Biarkan ada urutan angka dari 1 hingga n , yang disusun ulang secara acak. Seperangkat angka seperti itu memiliki sifat penting. Terdiri dari fakta bahwa tidak peduli bagaimana angka-angka ini didistribusikan pada baris yang berbeda dari matriks solusi sebagai posisi ratu (satu angka per baris), dua aturan pertama akan selalu dipenuhi dalam pernyataan masalah: setiap baris dan setiap kolom tidak akan memiliki lebih dari satu ratu. Namun, hanya sebagian dari posisi yang diperoleh akan bebas dari batasan diagonal. Bagian lain akan berada dalam kondisi "konflik" dengan ratu yang sudah ada sebelumnya. Untuk keluar dari situasi ini, penulis menggunakan metode membandingkan dan menukar posisi yang saling bertentangan untuk mendapatkan solusi yang lengkap. Dalam algoritme yang kami usulkan, situasi konflik tidak mungkin, karena pada setiap langkah penyelesaian masalah, ratu dipasang di sel garis yang dipertanyakan hanya jika sel itu bebas.

4.1 Memilih Model untuk Pelacakan Kembali (BT)

Dalam proses menemukan solusi untuk suatu masalah, sebuah situasi mungkin muncul ketika rantai solusi berurutan mengarah ke jalan buntu. Ini adalah properti "genetik" dari masalah non-deterministik. Dalam hal ini, Anda harus kembali ke salah satu langkah sebelumnya, mengembalikan keadaan tugas sesuai dengan level ini dan mulai lagi mencari solusi dari posisi ini. Pertanyaannya adalah level mana dari yang sebelumnya harus dikembalikan dan berapa level yang seharusnya (berdasarkan level, kami maksudkan langkah tertentu dalam menyelesaikan masalah dengan sejumlah ratu yang dipasang dengan benar). Jelas, memilih level solusi untuk kembali sama relevannya dengan memilih indeks baris atau indeks posisi di baris itu. Oleh karena itu, terlepas dari pendekatan untuk menyelesaikan masalah ini, perlu terlebih dahulu menentukan jumlah tingkat dasar untuk kembali, serta mekanisme dan kondisi untuk kembali ke salah satu tingkat ini. Dalam algoritma yang kami usulkan, kami membagi matriks solusi menjadi tiga level dasar. Ini adalah poin kembali. Jika, sebagai akibat dari solusi, kebuntuan terjadi, maka, tergantung pada parameter tugas, kami kembali ke salah satu dari tiga level dasar ini. Level dasar pertama ( baseLevel1 ) sesuai dengan keadaan saat verifikasi data komposisi yang dimaksud selesai. Ini adalah awal dari program. Nilai dari dua level dasar berikut ( baseLevel2 dan baseLevel3 ) tergantung pada ukuran matriks n . Ketergantungan empiris dari nilai-nilai dasar ini pada ukuran matriks solusi didirikan atas dasar sejumlah besar eksperimen komputasi. Untuk representasi yang lebih akurat dari ketergantungan ini, kami membagi seluruh interval yang dipertimbangkan dari 7 hingga 10 ⁸ menjadi dua bagian. Biarkan u = log (n) , lalu jika n <30 000 , maka

baseLevel2 = n - putaran (12.749568 * u3 - 46.535838 * u2 + 120.011829 * u - 89.600272)
baseLevel3 = n - putaran (9.717958 * u3 - 46.144187 * u2 + 101.296409 * u - 50.669273)

jika tidak

baseLevel2 = n - bulat (-0.886344 * u3 + 56.136743 * u2 + 146.486415 * u + 227.967782)
baseLevel3 = n - putaran (14.959815 * u3 - 253.661725 * u2 + 1584.713376 * u - 3060.691342)

4.2 Struktur blok

Algoritma dibangun dalam bentuk urutan lima blok peristiwa , di mana setiap peristiwa dikaitkan dengan eksekusi bagian tertentu dari solusi untuk masalah tersebut. Algoritma pemrosesan di setiap blok berbeda satu sama lain. Hanya tiga dari lima blok yang berfungsi membentuk rantai solusi berurutan, dan dua blok lainnya merupakan persiapan. Pilihan nomor blok tempat perhitungan dimulai tergantung pada nilai n dan pada hasil membandingkan ukuran komposisi k dengan nilai-nilai baseLeve2 dan baseLevel3 . Pengecualian adalah interval nilai n = (7, ..., 99) , yang dapat disebut "zona turbulen" karena kekhasan perilaku algoritma di bagian ini. Untuk nilai n = (7, ..., 49) , terlepas dari ukuran komposisi, setelah memasukkan dan memantau data, perhitungan dimulai dari blok ke-4. Untuk nilai n = (50, ..., 99) , tergantung pada ukuran komposisi, perhitungan dimulai dari blok kedua atau dari keempat. Seperti disebutkan di atas, pada setiap langkah penyelesaian masalah, hanya posisi-posisi dalam garis yang dianggap tidak termasuk dalam zona pembatasan yang dibuat oleh ratu yang telah didirikan sebelumnya. Posisi inilah yang disebut bebas .
Mari kita jelaskan secara singkat perhitungan apa yang dilakukan di masing-masing dari lima blok program ini.

4.3 Awal algoritma

Data dimasukkan dan komposisi diperiksa kebenarannya. Pada setiap langkah verifikasi, sel-sel array kontrol diubah. Jumlah ratu yang dipasang dengan benar dihitung. Jika tidak ada kesalahan dalam komposisi, solusi berlanjut, jika tidak, pesan kesalahan ditampilkan. Setelah verifikasi selesai, salinan array utama dibuat untuk digunakan kembali pada tingkat ini. Setelah itu, kontrol ditransfer ke Blok-1 .

4.4 Blok 1

Awal pembentukan cabang pencarian. Kami menganggap k queens yang terletak di papan catur sebagai posisi awal. Diperlukan untuk terus menyelesaikan komposisi ini dan menempatkan ratu di papan catur sampai jumlah totalnya sama dengan baseLevel2 . Algoritma yang digunakan di sini disebut randSet & randSet . Hal ini disebabkan oleh fakta bahwa di sini kita terus-menerus membandingkan dua daftar indeks acak, mencari pasangan yang bebas dari batasan diagonal yang sesuai. Untuk melakukan ini, tindakan berikut dilakukan:

a) dua daftar dibentuk: daftar indeks baris gratis dan daftar indeks kolom gratis;

b) menyusun ulang angka secara acak di masing-masing daftar ini;

c) dalam satu lingkaran, setiap pasangan nilai berturut-turut (i, j) , di mana indeks (i) dipilih dari daftar indeks baris gratis dan indeks (j) dari daftar indeks kolom gratis, dianggap sebagai posisi ratu potensial dan akan diperiksa apakah ini posisi di area proyeksi pengecualian diagonal.

Jika aturan pengecualian diagonal tidak dilanggar, maka posisinya dianggap benar, dan ratu ditempatkan di posisi ini. Setelah itu, penghitung bertambah untuk jumlah ratu yang dipasang dengan benar, dan sel-sel yang sesuai dari array kontrol diubah. Jika posisi (i, j) jatuh ke zona pembatasan diagonal yang dibentuk oleh ratu yang ditetapkan sebelumnya, maka tidak ada perubahan dan transisi ke pertimbangan pasangan nilai berikutnya terjadi.

Ketika siklus perbandingan semua pasangan daftar selesai, maka, berdasarkan indeks yang tersisa yang berada di zona pengecualian diagonal, daftar indeks baris bebas yang tersisa dan kolom bebas dibentuk lagi, dan prosedur ini diulangi hingga jumlah total ratu yang ditempatkan dengan benar (totPos ) tidak akan sama dengan atau melebihi nilai batas baseLevel2 . Setelah kondisi ini dipenuhi, kontrol ditransfer ke Blok-2 . Jika ternyata sebagai hasil pencarian solusi, muncul situasi dari seluruh daftar indeks baris bebas dan kolom bebas yang tersisa, tidak ada pasangan yang cocok untuk lokasi ratu, maka dalam hal ini, nilai asli array kontrol dipulihkan berdasarkan salinan yang dibuat sebelumnya , dan kontrol ditransfer ke awal Blok-1 untuk penghitungan ulang.

4.5 Blok 2

Blok ini berfungsi sebagai tahap persiapan untuk transisi ke Blok-3 . Pada level ini, jumlah baris bebas yang tersisa ( freeRows ) secara signifikan kurang dari n . Ini memungkinkan Anda untuk mentransfer peristiwa dari matriks asli ukuran nxn ke matriks berukuran lebih kecil L (1: freeRows, 1: freeRows) . Selain itu, berdasarkan pada informasi tentang baris bebas yang tersisa dan kolom bebas dalam matriks keputusan asli, nol dituliskan ke sel yang sesuai dari array L , yang menunjukkan bahwa sel-sel ini bebas. Dengan transisi "proyeksi" ini , korespondensi indeks baris dan kolom dari matriks baru dengan indeks yang sesuai dari matriks asli dipertahankan. Penting untuk dicatat bahwa meskipun, dalam proses penyelesaian masalah ini, semua peristiwa terungkap pada matriks awal ukuran nxn , dan matriks semacam itu adalah arena tindakan utama, dalam kenyataannya matriks ini tidak dibuat , dan hanya mengontrol array akuntansi untuk indeks baris A (1: n) dan kolom B (1: n) dari matriks ini.

Bersama dengan array L, dua array yang bekerja rAr (1: freeRows) dan tAr (1: freeRows) juga dibentuk di blok ini untuk menyimpan indeks yang sesuai dari array kontrol D1 dan D2 . Ini disebabkan oleh fakta bahwa ketika kita menginstal ratu berikutnya dalam sel (i, j) dari matriks awal ukuran nxn , maka setelah itu kita harus mengecualikan sel-sel dari array L yang jatuh ke zona proyeksi pengecualian diagonal dari array "besar" yang asli. Karena kontrol kendala diagonal dilakukan hanya dalam matriks asli ukuran nxn , keberadaan array yang bekerja rAr dan tAr memungkinkan kita untuk mempertahankan korespondensi dan menerjemahkan sel terlarang ke batas array L. Ini sangat menyederhanakan penghitungan posisi yang dikecualikan.
Setelah menyelesaikan pekerjaan persiapan di blok ini, salinan array utama dibuat untuk digunakan kembali pada tingkat ini, dan kontrol ditransfer ke Blok-3 .

4.6 Blok 3

Di blok ini, pembentukan cabang pencarian solusi berlanjut berdasarkan data yang disiapkan di blok sebelumnya. Jumlah baris di mana ratu diatur dengan benar sama dengan atau lebih besar dari baseLevel-2 . Anda harus terus memilih sampai jumlah ratu yang dipasang sama dengan baseLevel-3 . Di sini kita menggunakan algoritma pencarian rand & rand solution, yaitu untuk membentuk posisi ratu, alih-alih daftar indeks gratis, hanya dua indeks yang digunakan, nilai indeks acak dari baris bebas dan nilai indeks acak dari posisi bebas di baris ini. Prosedur ini diulang secara siklis sampai jumlah total ratu yang ditempatkan sama dengan nilai baseLevel-3 . Segera setelah kondisi ini dipenuhi, kontrol dipindahkan ke Blok-4 . Jika, sebagai hasil perhitungan, cabang pencarian ternyata buntu, maka bagian formasi cabang pencarian ini ditutup dan kembali ke awal Blok 3 , dari mana perhitungan diulangi lagi. Untuk ini, nilai awal semua array kontrol dipulihkan.

4.7 Blok 4

Di blok ini, data disiapkan untuk transfer kontrol ke Blok-5 . Untuk langkah ini, setelah menyelesaikan prosedur di Blok-3 , jumlah garis bebas ( nRow ) menjadi semakin sedikit. Oleh karena itu, juga bermanfaat untuk menerjemahkan acara dari array yang lebih besar ke array yang lebih kecil. Pendekatan ini memberi kita kesempatan untuk dengan cepat menentukan karakteristik yang diperlukan untuk garis yang tersisa yang kita butuhkan pada tahap ini. Yang sangat penting adalah kenyataan bahwa berdasarkan array seperti itu, dimungkinkan untuk memprediksi prospek cabang pencarian untuk banyak langkah ke depan tanpa harus menyelesaikan perhitungan. Kondisinya cukup sederhana. Jika ternyata di antara garis bebas yang tersisa ada garis di mana tidak ada posisi bebas, maka cabang pencarian yang dipertimbangkan ditutup dan kontrol ditransfer ke salah satu blok tingkat bawah. Tindakan persiapan yang dilakukan di sini sebagian besar mirip dengan apa yang dilakukan di Blok-2 . Berdasarkan indeks asli dari baris bebas dan kolom bebas, array 2 dimensi baru dibentuk, nilai nol yang sesuai dengan posisi bebas dalam matriks solusi asli. Selain itu, array khusus E (1: nRow, 1: nRow) dibuat di blok ini, berdasarkan di mana Anda dapat menentukan jumlah posisi bebas di garis bebas yang tersisa yang akan ditutup jika Anda memilih posisi (i, j) untuk mengatur ratu dalam matriks sumber. Sebelum mentransfer kontrol ke Blok 5 , tindakan berikut dilakukan:

a) jumlah posisi kosong di semua jalur yang tersisa ditentukan,

b) array jumlah posisi bebas, untuk baris yang dimaksud, diurutkan dalam urutan menaik,

c) jika semua jalur bebas yang tersisa memiliki posisi bebas (mis. nilai minimum dalam daftar peringkat ini berbeda dari 0), maka kontrol ditransfer ke Blok-5.

Jika ternyata di salah satu baris yang tersisa tidak ada posisi bebas, maka array yang diperlukan dikembalikan berdasarkan salinan yang disimpan, dan, tergantung pada parameter tugas, kontrol ditransfer ke salah satu level dasar.

d) salinan cadangan dari semua larik kontrol untuk tingkat 4 ini dibentuk.

4.8 Blok 5

Tahap ini adalah final, dan di sini, pembentukan cabang pencarian dilakukan lebih "seimbang" dan "rasional". Ini adalah "last mile", hanya sejumlah kecil jalur bebas yang tersisa. Tetapi pada saat yang sama, ini adalah bagian yang paling sulit. Semua kesalahan yang berpotensi dilakukan pada tahap-tahap sebelumnya dari pembentukan cabang pencarian solusi, secara agregat muncul di sini - dalam bentuk kurangnya posisi bebas di garis.

Algoritma dari blok ini dieksekusi atas dasar dua loop bersarang, di mana loop ketiga dieksekusi. Fitur dari siklus ketiga adalah dapat diulangi, tanpa mengubah parameter dari dua siklus eksternal. Ini terjadi jika cabang pencarian yang dihasilkan menemui jalan buntu. Jumlah pengulangan seperti itu tidak melebihi nilai batas repeatBound , nilai optimal yang ditetapkan atas dasar eksperimen komputasi.

Indeks loop luar dikaitkan dengan pilihan indeks baris berurutan yang tetap bebas setelah perhitungan di tingkat dasar ketiga. Ini dilakukan berdasarkan daftar baris yang sebelumnya diperingkat dengan jumlah posisi bebas di baris. Seleksi dimulai dengan garis, dengan jumlah minimum posisi bebas dan kemudian, dalam langkah-langkah berikutnya, dalam urutan menaik. Di dalam siklus ini, siklus kedua terbentuk, indeks yang berulang atas indeks semua posisi bebas di baris yang dimaksud. Tujuan dari siklus pertama hanya untuk memilih indeks dari salah satu garis bebas pada level ini. Dengan demikian, tujuan dari siklus kedua hanya untuk memilih satu posisi bebas dalam garis yang dipertimbangkan. Tindakan ini hanya terjadi pada tingkat dasar ketiga. Setelah pilihan ini, jumlah ratu yang diinstal bertambah, dan sel-sel yang sesuai dari semua array kontrol diubah. Selanjutnya, kontrol ditransfer dalam siklus bersarang (ketiga), zona aktivitas yang sudah semua jalur bebas yang tersisa. Di dalam siklus ini, pilihan indeks baris dan pilihan posisi bebas di baris ini dilakukan berdasarkan aturan berikut:

a) Pilih jalur gratis . Semua garis bebas yang tersisa dipertimbangkan, dan jumlah posisi bebas ditentukan di setiap garis. Baris dipilih dengan jumlah posisi bebas minimal. Ini meminimalkan risiko yang terkait dengan kemungkinan mengecualikan posisi kosong terakhir di beberapa jalur yang tersisa di mana negara minimal dan kritis dalam hal jumlah posisi kosong ( aturan risiko minimum ). Kebetulan, dengan aturan ini dalam pikiran bahwa indeks siklus pertama di blok kelima ini dimulai dengan pemilihan baris berurutan dengan nilai minimum jumlah posisi bebas dalam satu baris. Jika pada beberapa langkah ternyata kedua garis memiliki jumlah posisi bebas minimum yang sama, maka indeks salah satu dari dua posisi yang tercantum pertama dalam daftar peringkat dipilih secara acak. Jika jumlah baris yang memiliki jumlah minimum posisi bebas yang sama lebih dari dua, maka indeks salah satu dari tiga posisi yang terdaftar pertama dalam daftar peringkat dipilih secara acak.

b) Pemilihan posisi bebas berturut-turut .Dari daftar semua posisi bebas pada baris yang dipermasalahkan, satu dipilih yang menyebabkan kerusakan minimal pada posisi kosong di semua baris yang tersisa. Ini dilakukan berdasarkan array E. yang dihasilkan sebelumnya. Dengan “kerusakan minimal”, kami maksudkan pilihan posisi seperti itu dalam garis yang diberikan yang mengecualikan paling sedikit jumlah posisi bebas di semua garis yang tersisa ( aturan kerusakan minimum)) Jika ternyata dua atau lebih posisi bebas berturut-turut memiliki nilai minimum yang sama sesuai dengan kriteria kerusakan, maka indeks salah satu dari dua posisi yang tercantum pertama dalam daftar dipilih secara acak. Memilih posisi yang mengecualikan jumlah minimum posisi bebas di garis yang tersisa meminimalkan "kerusakan" yang terkait dengan posisi ratu di posisi ini. Menggunakan kedua aturan ini memungkinkan penggunaan sumber daya yang lebih rasional di setiap langkah pembentukan cabang pencarian. Ini sangat mengurangi risiko dan meningkatkan kemungkinan memilih komposisi sewenang-wenang untuk solusi lengkap jika komposisi tersebut memiliki solusi. Jika pada beberapa langkah solusi ternyata di salah satu baris yang tersisa untuk dipertimbangkan tidak ada posisi kosong, maka cabang pencarian ini ditutup. Dalam hal ini,berdasarkan cadangan, semua larik kontrol dipulihkan, dan jika jumlah penghitung pengulangan tidak melebihi nilai batasrepeatBound, kemudian tanpa mengubah indeks siklus eksternal pertama dan kedua, pekerjaan siklus bersarang ketiga diulangi lagi. Ini disebabkan oleh fakta bahwa dalam kasus-kasus di mana nilai minimum dari kriteria yang relevan bertepatan, kami membuat pilihan acak. Pembentukan kembali cabang pencarian pada kondisi yang sama pada tingkat dasar memungkinkan penggunaan "sumber daya awal" yang lebih efisien yang disediakan pada tingkat ini. Jumlah awal yang berulang dari siklus bersarang ketiga terbatas, dan jika nilai batas terlampaui, operasi siklus ini terputus. Setelah itu, nilai array kontrol dipulihkan, dan kontrol ditransfer ke siklus level dasar ketiga untuk menuju ke nilai indeks berikutnya. Prosedur ini diulang secara siklis sampai diperoleh solusi lengkap, atau ternyata demikianbahwa kami menggunakan semua jalur bebas dan semua posisi bebas di jalur ini di tingkat dasar ini. Dalam hal ini, tergantung pada jumlah total perhitungan berulang pada berbagai level dasar, dan dengan mempertimbangkan ukuran matriks keputusan dan ukuran komposisi, seseorang kembali ke salah satu level yang lebih rendah untuk perhitungan berulang, atau penilaian dibuat bahwa komposisi yang dimaksud tidak dapat dilengkapi untuk menyelesaikan solusi. Dalam program ini, untuk membatasi waktu total tagihan, dapat diterima bahwa proseduratau penilaian dibuat bahwa komposisi tersebut tidak dapat diselesaikan sampai keputusan lengkap. Dalam program ini, untuk membatasi waktu total tagihan, dapat diterima bahwa proseduratau penilaian dibuat bahwa komposisi tersebut tidak dapat diselesaikan sampai keputusan lengkap. Dalam program ini, untuk membatasi waktu total tagihan, dapat diterima bahwa prosedurPelacakan Kembali , terlepas dari level mana sebelumnya yang dihasilkan, dapat dilakukan tidak lebih dari totSimBound kali. Nilai batas ini dipilih berdasarkan eksperimen komputasi untuk berbagai nilai n.

5. Analisis efektivitas algoritma seleksi

Efisiensi dari algoritma randSet & randSet . Untuk menganalisis kemampuan algoritma ini, percobaan komputasi dilakukan, yang terdiri dalam menempatkan ratu dalam matriks solusi berdasarkan pada model randSet & randSet selama kemungkinan ini ada. Segera setelah cabang pencarian mencapai jalan buntu, atau solusi lengkap diperoleh, ukuran komposisi, waktu solusi diperbaiki, dan tes diulangi lagi. Percobaan komputasi dilakukan untuk seluruh daftar dasar nilai n . Jumlah tes berulang untuk nilai n = (30, 40, ..., 90, 100, 200, 300, 500, 800, 1000) sama dengan satu juta , untuk nilai yang tersisa, jumlah tes, dengan peningkatan n, secara bertahap menurun dari 100000 menjadi 100. Analisis hasil eksperimen komputasi memungkinkan kita untuk menarik kesimpulan berikut:

a) Sebagai hasil dari hanya siklus pertama dari prosedur randSet & randSet, rata-rata sekitar 60% dari semua ratu ditempatkan dengan benar. Untuk n = 100, jumlah ratu yang ditempatkan dengan benar adalah 60,05%. Dengan peningkatan nilai n, nilai ini menurun secara bertahap, dan untuk n = 10 ⁷ berjumlah 59,97%.

b) Histogram distribusi nilai panjang komposisi yang diperoleh memiliki bentuk yang sama, terlepas dari ukuran matriks keputusan n. Selain itu, mereka semua memiliki fitur karakteristik - sisi kiri distribusi (dengan nilai modal) berbeda dari sisi kanan. Pada Gambar 2, sebagai contoh, histogram yang sesuai untuk


Gambar. 2. Histogram distribusi solusi dari berbagai panjang untuk model randSet & randSet ( n = 100, ukuran sampel = 10 ⁶ ).

n = 100. Tampaknya histogram dikumpulkan dari distribusi frekuensi dua peristiwa yang berbeda, karena frekuensi kejadian peristiwa di bagian kiri dan kanan distribusi berbeda. Untuk menggambarkan distribusi ini, kemungkinan besar cocok untuk menggunakan dua fungsi dari kepadatan distribusi normal, salah satunya mencakup interval ke nilai modal, yang lain - interval setelah nilai modal.

c) Nilai rata-rata jumlah ratu ( qMean ) yang dapat diatur dalam matriks keputusan berdasarkan algoritma ini meningkat dengan n . Seperti yang dapat dilihat dari Gambar 3, di mana grafik ketergantungan dari rasio qMean / n pada ukuran matriks n disajikan , rasio ini meningkat dengan peningkatan ukuran matriks. Misalnya,

Gbr. 3. Ketergantungan rasio qMean / n pada nilai n untuk berbagai ukuran matriks solusi. Modelnya adalah randSet & randSet , qMean adalah nilai rata-rata dari panjang solusi.

jika untuk matriks ukuran 100x100, algoritma untuk memilih posisi adalah randSet & randSetmemungkinkan "tanpa henti" untuk menempatkan ratu rata-rata di 89 baris, maka untuk matriks 1000x1000 , jumlah garis tersebut meningkat rata-rata menjadi 967.

d) Berdasarkan pada algoritma randSet & randSet, Anda bisa mendapatkan solusi lengkap, tetapi "produktivitas" dari pendekatan ini sangat rendah . Seperti dapat dilihat dari Gambar 4, untuk


Gambar. 4. Penurunan probabilitas untuk mendapatkan solusi lengkap dalam model randSet & randSet dengan peningkatan n .

nilai n = 7, probabilitas untuk mendapatkan solusi lengkap adalah 0,057 . Selanjutnya, dengan meningkatnya nprobabilitas mendapatkan solusi lengkap berkurang dengan cepat, mendekati nol secara asimptot. Mulai dari nilai n = 48, probabilitas untuk mendapatkan solusi lengkap adalah di urutan 10 ^-6 . Setelah nilai ambang n = 70, untuk nilai-nilai n berikutnya , tidak satu solusi lengkap diperoleh (dengan jumlah tes sama dengan satu juta ).

e) Model randSet & randSet menghasilkan cabang pencarian dengan kecepatan yang sangat tinggi. Untuk n = 1000, waktu rata-rata untuk mendapatkan komposisi adalah 0,0015 detik. Panjang rata-rata komposisi adalah 967. Dengan demikian, untuk n = 10 ⁶waktu rata-rata adalah 2,6754 detik dengan panjang lagu rata-rata 999793.

f) Kecuali untuk interval kecil n <= 70, ketika model randSet & randSet dalam kasus yang sangat langka dapat mengarah ke solusi yang lengkap, dalam semua kasus cabang keputusan berakhir dengan pembentukan komposisi negatif, yang tidak dapat diselesaikan sampai solusi lengkap. Jadi algoritma randSet & randSetIni memiliki keuntungan penting - kecepatan tinggi pembentukan cabang pencarian, dan kelemahan yang signifikan adalah bahwa jika ukuran komposisi melebihi nilai ambang batas tertentu, algoritma ini mengarah pada pembentukan komposisi yang tidak dapat diselesaikan hingga solusi lengkap. Untuk mengatasi kelemahan ini, kami menghentikan pembentukan cabang pencarian ketika ambang baseLevel-2 tercapai .

Efisiensi algoritma rand & rand . Untuk menentukan kemampuan algoritma rand & rand , simulasi komputer yang cukup rinci dilakukan untuk daftar dasar nilai n . Seperti halnya model randSet & randSet, jumlah tes ulang dalam banyak kasus sama dengan satu juta . Untuk nilai-nilai lain, jumlah tes secara bertahap menurun dari 100.000 menjadi 100.

Kedua algoritma didasarkan pada prinsip seleksi acak. Oleh karena itu, harus diharapkan bahwa kesimpulan yang ditarik di sini pada dasarnya akan identik dengan kesimpulan yang dirumuskan untuk model randSet & randSet . Namun, ada perbedaan mendasar di antara mereka, dan itu terdiri dari yang berikut:

a) model rand & rand tidak bekerja "keras" seperti model randSet & randSet . Jika kita berbicara tentang "indeks penggunaan peluang yang disediakan secara rasional," model rand & randpada setiap langkah menggunakan sumber daya lebih rasional. Ini mengarah pada fakta bahwa, misalnya, pada n = 30, probabilitas untuk mendapatkan solusi lengkap 0,00170 dalam model ini adalah 15 kali lebih besar dari nilai yang sama 0,00011 untuk model randSet & randSet . Selain itu, di sini, hingga nilai ambang n = 370, probabilitas untuk mendapatkan setidaknya satu solusi lengkap selama satu juta tes tetap. Setelah nilai ambang ini, untuk nilai selanjutnya dari n dengan jumlah tes sama dengan satu juta, tidak satu solusi lengkap diperoleh berdasarkan model rand & rand .

b) algoritma ini jauh lebih lambat daripada algoritma randSet & randSet . Jika untukn = 1000 untuk menghasilkan komposisi ukuran 967, waktu rata-rata untuk mendapatkan satu komposisi adalah 0,0497 detik, yaitu 33 lebih dari nilai yang sesuai 0,0015 untuk model randSet & randSet .

Alasan perbedaan antara dua metode seleksi acak yang pada dasarnya serupa adalah karena kenyataan bahwa dalam model randSet & randSet , untuk mempercepat perhitungan, pemilihan acak dari daftar yang tersisa tidak dilakukan pada setiap langkah. Sebagai gantinya, sepasang indeks dipilih secara berurutan dari dua daftar, yang unsur-unsurnya disusun secara acak. Seleksi semacam itu tidak acak pada tingkat penuh, namun, itu cocok dengan logika masalah dan memungkinkan Anda untuk dengan cepat menghitung.

Untuk secara visual menunjukkan operasi algoritma rand & rand, percobaan berikut dilakukan:

a) Untuk papan catur ukuran 100x100, setelah setiap langkah dari lokasi ratu dalam garis apa pun, jumlah posisi bebas di masing-masing garis bebas yang tersisa ditentukan. Dengan demikian, setelah setiap langkah menyelesaikan masalah, kami menerima daftar jalur bebas dan daftar terkait jumlah posisi bebas di jalur ini. Ini memungkinkan untuk membuat grafik di mana indeks kolom dari matriks tersebut diplot sepanjang sumbu absis, dan jumlah posisi bebas yang tersisa di sepanjang sumbu ordinat. Sebagai perbandingan, perhitungan juga dilakukan untuk model pemilihan posisi berurutan. Dengan pemilihan berurutan dimaksudkan sebagai berikut. Baris pertama dipertimbangkan, di mana posisi bebas pertama dalam daftar dipilih. Kemudian, baris kedua dipertimbangkan, di mana posisi bebas pertama dalam daftar, dll. Juga dipilih. Dalam Gambar 5 dan 6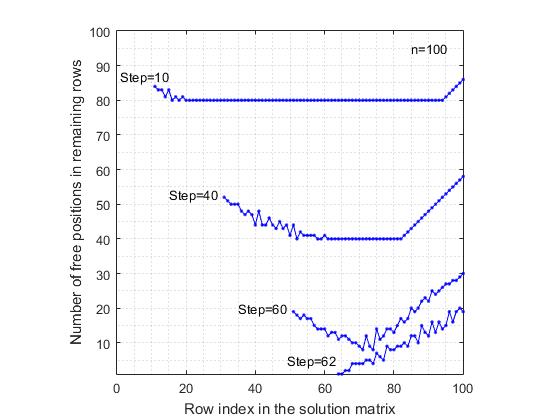


Fig. 5. Mengurangi jumlah posisi bebas di garis bebas yang tersisa setelah penempatan ratu. Pemilihan posisi secara teratur dan berurutan.

Hasil yang sesuai dengan model yang dipertimbangkan disajikan. Untuk kejelasan, grafik menunjukkan hasil hanya setelah langkah-langkah (10, 40, 60). Untuk model posisi pemilihan berurutan, yang terakhir adalah grafik setelah langkah ke-62, karena cabang pencarian berakhir karena kurangnya posisi bebas di baris ke-63. Di sisi lain, dalam model rand & rand , grafik terakhir disajikan setelah langkah ke-70 menempatkan ratu, meskipun di sini, jumlah rata-rata ratu yang ditempatkan dengan benar mencapai 89, yang merupakan 26 langkah lebih banyak daripada dalam model berurutan. Tampilan grafik yang aneh dalam model rand & randkarena fakta bahwa indeks baris dipilih secara acak di antara baris bebas yang tersisa, dan oleh karena itu mereka tersebar secara acak di seluruh matriks solusi. Perbandingan kedua angka ini menunjukkan bahwa dalam model pemilihan posisi berurutan, kisaran variabilitas jumlah posisi bebas lebih tinggi daripada model rand & rand . Hal ini disebabkan oleh fakta bahwa dengan seleksi reguler, kendala diagonal yang tidak seragam mengecualikan posisi bebas di baris yang tersisa, yang mengarah pada fakta bahwa dalam beberapa baris tingkat pengurangan jumlah posisi kosong lebih tinggi daripada di baris lainnya.


Fig. 6. Mengurangi jumlah posisi bebas di garis bebas yang tersisa setelah penempatan ratu. Model penentuan posisi adalah rand & rand .

Sebaliknya, dengan pemilihan acak dari indeks baris bebas dan indeks kolom bebas, posisi ratu didistribusikan secara merata di atas "area" dari matriks keputusan, yang mengurangi tingkat "rata-rata" pengurangan jumlah posisi bebas di baris yang tersisa. Jadi, dengan mempertimbangkan kemampuan algoritma rand & rand , kami menggunakannya dalam program untuk melanjutkan pembentukan cabang pencarian solusi sampai level baseLevel-3 tercapai .

Perlu dicatat bahwa meskipun algoritma seleksi ( randSet & randSet, rand & rand ) tidak begitu efisien, kita masih harus menggunakan beberapa metode pemilihan acak lainnya ketika mengembangkan algoritma. Ini karena pernyataan masalahnya.Masalah penyelesaian n-Queens . Jika kita membayangkan bahwa ada algoritma optimal tertentu yang memecahkan masalah, maka pada input algoritma seperti itu akan selalu menerima seperangkat indeks baris dan kolom acak tertentu. Setiap kali itu akan menjadi kumpulan indeks baris dan kolom acak baru dari berbagai kemungkinan. Agar dapat "menerima" algoritma seperti berbagai komposisi acak, algoritma itu sendiri harus dibangun berdasarkan seleksi acak. Pencocokan harus seperti kunci kunci . Jika kita membuat algoritma berdasarkan prinsip ini, maka komposisi yang konsisten dari kratu akan dianggap sebagai posisi awal (awal) dalam siklus pengambilan keputusan. Dan lebih jauh, tujuannya hanya akan melanjutkan pembentukan cabang pencarian solusi sampai solusi untuk komposisi yang diberikan ditemukan, atau terbukti bahwa solusi seperti itu tidak ada.

6. Contoh penggunaan aturan risiko minimum (n = 100)

Pada tahap awal menemukan solusi, ketika jumlah posisi bebas di baris tidak kritis, maka pilihan indeks baris bebas, atau indeks posisi di baris ini, tidak fatal. Namun, pada tahap terakhir, ketika jumlah posisi bebas di beberapa baris adalah 1 atau 2, maka dalam hal ini, Anda harus memilih algoritma pemilihan yang berbeda. Pada level ini, algoritma pilihan acak randSet & randSet dan rand & rand tidak lagi berfungsi.

Alasan mengapa algoritma pemilihan acak tidak akan berfungsi dapat dijelaskan dengan contoh sederhana berikut ini. Biarkan pada beberapa langkah pemecahan masalah, untuk nilai n sembarang dari n, di baris tersisa i ₁ , i ₂ , ..., i _kjumlah posisi kosong (ditunjukkan dalam tanda kurung) adalah: i ₁ (1), i ₂ (2), i ₃ (4), i ₄ (5), i ₅ (3), i ₆ (4) , dll. Jika Anda memilih secara acak baris mana pun, tetapi bukan baris ₁ , di mana hanya ada satu posisi bebas, ini dapat menyebabkan situasi risiko ketika larangan diagonal terkait dengan posisi ratu di baris yang dipilih dapat menyebabkan penutupan satu-satunya posisi bebas di baris. i ₁ , yang akan menyebabkan solusi macet. Dari semua baris i ₁ , i ₂ , ..., i _kyang paling rentan dan peka terhadap pilihan indeks baris adalah baris i ₁ . Dalam situasi seperti itu, Anda harus terlebih dahulu memilih baris yang statusnya paling kritis dan menciptakan risiko untuk menyelesaikan masalah. Oleh karena itu, pada tahap terakhir penyelesaian masalah, pada setiap langkah perlu untuk memilih posisi garis berdasarkan algoritma sederhana dengan risiko minimal.

Untuk kejelasan, mari kita perhatikan, sebagai contoh, untuk matriks 100 x 100 , tahap terakhir dalam pembentukan beberapa solusi nyata, setelah langkah ke-88. Hingga tugas selesai, 12 garis bebas tetap, untuk masing-masing jumlah posisi bebas ditemukan (garis-garis tersebut diperingkat dalam urutan peningkatan jumlah posisi bebas):Langkah-89 - 25 (1), 12 (2), 22 (2), 82 (2), 88 (2), 7 (3), 64 (3), 3 (4), 76 (4), 91 (4), 4 (5), 96 (5) - menunjukkan indeks garis bebas, dan dalam tanda kurung - jumlah posisi bebas di garis ini. Menurut aturan risiko minimum, pada langkah ke 89 untuk menyelesaikan masalah, baris 25 dipilih dan satu posisi bebas yang ada di dalamnya. Sebagai hasil penghitungan ulang, kami memiliki 11 jalur bebas tersisa: Langkah-90 - 7 (2), 12 (2), 22 (2), 82 (2), 88 (2), 3 (3), 64 (3), 76 (3), 4 (4), 91 (4), 96 (4).Seperti yang Anda lihat, jumlah posisi bebas di lima baris pertama adalah sama dan sama dengan 2. Oleh karena itu, indeks salah satu dari tiga baris pertama dipilih secara acak. Dalam hal ini, baris ke-12 dipilih dan posisi dua yang tersisa di baris ini, yang mengarah ke kerusakan minimal. Jadi, pada langkah ke-91 dari pembentukan larutan, kami memiliki 10 garis bebas: Langkah-91 - 22 (1), 3 (2), 7 (2), 82 (2), 88 (2), 64 (3) 76 (3), 91 (3), 4 (4), 96 (4) . Pada langkah ini, baris 22 dipilih dan satu posisi bebas yang ada di dalamnya. Melanjutkan dengan cara yang sama, urutan keputusan berikut ini dibentuk (Tabel 1). Indeks dari baris yang dipilih ditampilkan dalam huruf tebal.

Dalam contoh khusus ini, dalam 11 kasus dari 12, ada situasi ketika dalam daftar saluran bebas yang tersisa ada setidaknya satu baris di mana hanya satu posisi bebas yang tersisa. Jika kami tidak menggunakan aturan risiko minimum, kami tidak akan dapat mencapai tujuan. Karena satu "gerakan salah" dalam memilih indeks dari garis bebas, kemungkinan besar akan mengarah pada penghancuran satu-satunya posisi bebas yang ada di salah satu garis bebas yang tersisa. Ini adalah alasan bahwa ketika hanya menggunakan algoritma randSet x randSet atau rand x rand untuk mendapatkan solusi yang lengkap, pada tahap terakhir, solusi tersebut menemui jalan buntu.
Perlu dicatat bahwa algoritma risiko minimum memiliki makna sehari-hari yang sederhana, dan sering digunakan dalam pengambilan keputusan. Sebagai contoh, dokter pertama-tama beroperasi pada pasien yang kondisinya paling kritis seumur hidup, seperti halnya petani, selama kekeringan parah, mencoba menyelamatkan tanaman, pertama-tama menyirami daerah-daerah yang berada dalam kondisi paling kritis ...

7. Analisis efisiensi algoritma

Untuk mengevaluasi efisiensi algoritma untuk berbagai nilai n, percobaan komputasi yang cukup panjang (dalam hal waktu total) dilakukan. Awalnya, algoritma yang cukup cepat dikembangkan untuk menghasilkan array solusi nQueens Problem untuk nilai arbitrer n. Kemudian, berdasarkan program ini, sampel besar solusi dibentuk untuk daftar dasar nilai n. Ukuran sampel yang diperoleh dari solusi nQueens Problem untuk berbagai nilai n, masing-masing, sama: (10) - 1000, (20, 30, ..., 90, 100, 200, 300, 500, 800, 800, 800, 1000, 3000, 5000, 10.000) - -10000, (30000, 50000, 80000) - 5000, (105, 3 * 105) - 3000, (5 * 105, 8 * 105, 106) - 1000, (3 * 106) - 300, ( 5 * 106) - 200, (10 * 106) - 100, (30 * 106) - 50, (50 * 106) - 30, (80 * 106, 100 * 106) - 20. Di sini, dalam tanda kurung, daftar nilai n ditunjukkan, dan tanda hubung ganda menunjukkan ukuran sampel dari solusi yang diperoleh.Setelah itu, komposisi acak dengan ukuran acak dibentuk berdasarkan masing-masing sampel larutan. Misalnya, untuk masing-masing 10.000 solusi untuk n = 1000, 100 komposisi acak ukuran arbitrer dibentuk. Hasilnya adalah sampel satu juta lagu. Karena setiap komposisi ukuran sewenang-wenang, yang dibentuk berdasarkan solusi yang ada, dapat diselesaikan setidaknya satu kali hingga solusi lengkap, tugasnya adalah menyelesaikan setiap komposisi dari sampel yang dihasilkan hingga solusi lengkap berdasarkan pada algoritma solusi masalah penyelesaian n-Queens Completion Problem . Karena dalam algoritma yang dipertimbangkan pada setiap langkah, penempatan ratu yang benar di papan catur diperiksa, di sini, pada prinsipnya, mereka tidak dapatkomposisi acak dengan ukuran acak dibentuk atas dasar masing-masing sampel larutan. Misalnya, untuk masing-masing 10.000 solusi untuk n = 1000, 100 komposisi acak ukuran arbitrer dibentuk. Hasilnya adalah sampel satu juta lagu. Karena setiap komposisi ukuran sewenang-wenang, yang dibentuk berdasarkan solusi yang ada, dapat diselesaikan setidaknya satu kali hingga solusi lengkap, tugasnya adalah menyelesaikan setiap komposisi dari sampel yang dihasilkan hingga solusi lengkap berdasarkan pada algoritma solusi masalah penyelesaian n-Queens Completion Problem . Karena dalam algoritma yang dipertimbangkan pada setiap langkah, penempatan ratu yang benar di papan catur diperiksa, di sini, pada prinsipnya, mereka tidak dapatkomposisi acak dengan ukuran acak dibentuk atas dasar masing-masing sampel larutan. Misalnya, untuk masing-masing 10.000 solusi untuk n = 1000, 100 komposisi acak ukuran arbitrer dibentuk. Hasilnya adalah sampel satu juta lagu. Karena setiap komposisi ukuran sewenang-wenang, dibentuk berdasarkan solusi yang ada, dapat diselesaikan setidaknya satu kali hingga solusi lengkap, tugasnya adalah untuk menyelesaikan setiap komposisi dari sampel yang dihasilkan ke solusi lengkap berdasarkan pada algoritma solusi masalah penyelesaian n-Queens Completion Problem . Karena dalam algoritma yang dipertimbangkan pada setiap langkah, penempatan ratu yang benar di papan catur diperiksa, di sini, pada prinsipnya, mereka tidak dapat100 komposisi acak ukuran acak dibentuk. Hasilnya adalah sampel satu juta lagu. Karena setiap komposisi ukuran sewenang-wenang, yang dibentuk berdasarkan solusi yang ada, dapat diselesaikan setidaknya satu kali hingga solusi lengkap, tugasnya adalah menyelesaikan setiap komposisi dari sampel yang dihasilkan hingga solusi lengkap berdasarkan pada algoritma solusi masalah penyelesaian n-Queens Completion Problem . Karena dalam algoritma yang dipertimbangkan pada setiap langkah, penempatan ratu yang benar di papan catur diperiksa, di sini, pada prinsipnya, mereka tidak dapat100 komposisi acak ukuran acak dibentuk. Hasilnya adalah sampel satu juta lagu. Karena setiap komposisi ukuran sewenang-wenang, yang dibentuk berdasarkan solusi yang ada, dapat diselesaikan setidaknya satu kali hingga solusi lengkap, tugasnya adalah menyelesaikan setiap komposisi dari sampel yang dihasilkan hingga solusi lengkap berdasarkan pada algoritma solusi masalah penyelesaian n-Queens Completion Problem . Karena dalam algoritma yang dipertimbangkan pada setiap langkah, penempatan ratu yang benar di papan catur diperiksa, di sini, pada prinsipnya, mereka tidak dapatmaka tugasnya adalah menyelesaikan setiap komposisi dari sampel yang dihasilkan, berdasarkan pada algoritma solusi Masalah penyelesaian n-Queens, menjadi solusi lengkap. Karena dalam algoritma yang dipertimbangkan pada setiap langkah, penempatan ratu yang benar di papan catur diperiksa, di sini, pada prinsipnya, mereka tidak dapatmaka tugasnya adalah menyelesaikan setiap komposisi dari sampel yang dihasilkan, berdasarkan pada algoritma solusi Masalah penyelesaian n-Queens, menjadi solusi lengkap. Karena dalam algoritma yang dipertimbangkan pada setiap langkah, penempatan ratu yang benar di papan catur diperiksa, di sini, pada prinsipnya, mereka tidak dapatKeputusan Positif Palsu (mis. Keputusan salah yang kami anggap salah, benar). Namun, mungkin ada solusi False Negative - dalam hal komposisi apa pun yang terbentuk berdasarkan solusi yang ada tidak diselesaikan oleh program sampai solusi selesai (walaupun kita tahu bahwa semua komposisi memiliki solusi). Melakukan eksperimen komputasi dalam rentang n nilai yang begitu luas, kami menetapkan sendiri sasaran berikut:

a) untuk menentukan kompleksitas waktu dari algoritma,

b) untuk menentukan probabilitas solusi Negatif Salah yang muncul untuk berbagai nilai n,

c) untuk menentukan frekuensi penggunaan prosedur Pelacakan Kembali untuk nilai n yang berbeda.

Hasil percobaan komputasi tersebut disajikan pada tabel 2.

Kesimpulan umum yang dapat ditarik berdasarkan hasil yang diperoleh adalah sebagai berikut:

a) Algoritma bekerja cukup cepat. Misalnya, waktu kompilasi rata-rata komposisi sewenang-wenang untuk papan catur ukuran 1000 x 1000 , yang diperoleh berdasarkan satu juta eksperimen komputasi, adalah 0,062157 detik. Ini berarti bahwa jika komposisi memiliki solusi, maka akan segera ditemukan setelah menekan tombol "Enter" . Waktu kompilasi rata-rata komposisi sewenang-wenang, untuk semua nilai n , dalam kisaran 7 hingga 30.000, tidak melebihi satu detik.

b) Dalam setiap sampel, ada sekitar 10% komposisi, yang membutuhkan lebih banyak waktu untuk menyelesaikannya. Komposisi semacam itu membentuk ekor kanan panjang dalam histogram distribusi. Jika kita mengecualikan 10% komposisi ini dan melakukan perhitungan untuk sisa 90% solusi, maka waktu perhitungan ( _rata-rata t90 ) akan jauh lebih sedikit. Misalnya, untuk papan catur 1000 x 1000 , waktu penghitungan rata-rata adalah 0,027727 detik, yaitu 2,24 kali lebih kecil dari waktu rata-rata yang diperoleh dari seluruh sampel.

c) Untuk nilai n≤800 , dalam sampel komposisi ada yang tidak dapat diselesaikan sampai solusi lengkap. Ini adalah False Negativekeputusan. Dalam batas yang ditentukan dalam program, yang memungkinkan prosedur Pelacakan Kembali dilakukan hingga 1000 kali, algoritma gagal menyelesaikan komposisi ini. Mereka secara keliru diklasifikasikan sebagai komposisi negatif, yaitu mereka yang tidak punya solusi. Jumlah solusi Negatif Palsu seperti itu tidak signifikan, dan bagian mereka dalam sampel kurang dari 0,0001. Lebih lanjut, ketika n meningkat , proporsi solusi Negatif Palsu berkurang. Untuk semua nilai n > 800, dalam rangkaian eksperimen komputasi ini, tidak ada satu pun kasus solusi Negatif Salah . Namun, jelas bahwa jika ukuran sampel meningkat berkali-kali, kemungkinan munculnya False Negative tidak dikecualikan.solusi, meskipun kemungkinan kejadian seperti itu akan menjadi jumlah yang sangat kecil.

Kompleksitas waktu dari algoritma . Gambar 7 menunjukkan grafik perubahan waktu pengambilan rata-rata komposisi acak untuk berbagai nilai n .


Fig. 7. Ketergantungan waktu pengambilan rata-rata ( t ) dari komposisi acak pada ukuran ( n ) dari matriks keputusan.

Logaritma desimal dari nilai n diplot pada sumbu absis , dan logaritma, meningkat 1000 kali, dari waktu penghitungan rata-rata, diplot pada sumbu ordinat. Untuk kejelasan, gambar tersebut juga menunjukkan garis putus-putus dari diagonal kuadran. Dapat dilihat bahwa waktu pengambilan meningkat secara linear dengan peningkatan n. Seluruh rentang n dari 50 hingga 10 ⁸nilai-nilai eksperimental dari waktu penghitungan membentuk garis lurus, yang dengan korelasi yang cukup tinggi ( R = 0,9998 ) dijelaskan oleh

log persamaan regresi linier (1000 * t) = - 0,628927 + 0,781568 * log (n)

Sedikit penyimpangan dari tren umum hanya khas untuk nilai n = ( 10, ... 49) , yang disebabkan oleh fakta bahwa hanya blok perhitungan kelima yang digunakan dalam kisaran ini untuk menyelesaikan masalah, algoritma yang berbeda secara signifikan dari operasi algoritma dari blok pertama dan ketiga. Dalam ketergantungan yang dihasilkan, koefisien linier ( 0,781568) kurang dari satu, yang mengarah pada fakta bahwa dengan meningkatnya nilai n, garis regresi dan diagonal kuadran diverge. Untuk menjelaskan dengan jelas alasan perbedaan tersebut alih-alih waktu awal, kami mempertimbangkan waktu rata-rata yang diperlukan untuk lokasi satu ratu pada satu baris, mis. bagi waktu penghitungan rata-rata dengan n . Kami menyebut indikator semacam itu sebagai pengurangan waktu . Jelas, jika pengurangan waktu tidak berubah dengan meningkatnya n , maka solusi seperti itu akan linier ( O (n) ). Seperti yang terlihat pada Gambar 8, di mana plot logaritma dari waktu yang diberikan,


Gambar. 8 Ketergantungan waktu rata-rata ( t _baris), yang diperlukan agar ratu ditempatkan pada satu garis arbitrer, dari ukuran ( n ) matriks solusi.

( tRow ), meningkat 10 ⁶ kali, dari logaritma ukuran matriks solusi, dalam kisaran n dari 50 hingga 10 ⁸ , waktu yang berkurang berkurang dengan meningkatnya n . Jika pengurangan waktu untuk n = 50 adalah 10.7146 * 10 ^-6 detik, maka waktu yang sesuai untuk n = 10 ⁸ dikurangi sebesar 21 kali dan 0,5084 * 10 ^-6detik. Perilaku algoritma seperti itu, pada pandangan pertama, tampak keliru, karena tidak ada alasan obyektif mengapa algoritma akan menganggapnya lebih lambat untuk nilai n kecil daripada nilai besar. Namun, tidak ada kesalahan, dan ini adalah properti objektif dari algoritma ini. Ini disebabkan oleh fakta bahwa algoritma ini adalah komposisi dari tiga algoritma yang beroperasi pada kecepatan yang berbeda. Selain itu, jumlah baris yang diproses oleh masing-masing algoritma ini berubah dengan meningkatnya nilai n. Karena alasan inilah waktu penghitungan meningkat dalam rentang nilai awal n = (10, 20, 30, 40), karena semua perhitungan di area kecil ini dilakukan hanya berdasarkan blok prosedur kelima, yang bekerja sangat efisien, tetapi tidak secepat blok prosedur pertama. Jadi, mengingat bahwa waktu penghitungan diperlukan untuk memposisikan sang ratu pada satu baris,berkurang dengan meningkatnya ukuran papan catur, kompleksitas waktu dari algoritma ini dapat disebut menurun - linear.

Frekuensi Pelacakan Kembali (BT) telah digunakan . Dalam semua kasus percobaan komputasi, kami melacak jumlah kasus menggunakan prosedur BT dalam menyelesaikan setiap masalah. Penjumlahan kumulatif dibuat dari semua kasus menggunakan BT, terlepas dari tingkat dasar apa yang dikembalikan ke dalam proses menemukan solusi. Ini memberi kami kesempatan untuk menentukan, untuk setiap sampel, proporsi keputusan-keputusan di mana prosedur BT tidak pernah digunakan. Gambar 9 menunjukkan


Gambar. 9. Persentase solusi sampel di mana prosedur Kembali Tracking pernah menggunakan

grafik yang menunjukkan bagaimana proporsi solusi tanpa prosedur BT ( Nol Kembali Tracking ) dengan peningkatan nilai n. Dapat dilihat bahwa dalam kisaran nilai n = (7, ..., 100000) , jumlah solusi di mana prosedur BT tidak pernah digunakan melebihi 35%. Selain itu, dalam kisaran nilai n = (320, ..., 22500) , jumlah kasus tersebut melebihi 50%. Hasil yang paling efektif diperoleh untuk papan catur dengan ukuran 5000 x 5000 , di mana, dalam sampel 10.000 komposisi, dalam 61,92% kasus solusi "deterministik" dari masalah non-deterministik dilakukan , karena Prosedur BT pada 61,92%kasing tidak pernah digunakan. Dalam solusi yang tersisa, dalam 21,87% kasus, prosedur BT digunakan 1 kali, pada 9,07% kasus - 2 kali, dan dalam 3,77% kasus - 3 kali. Bersama-sama, ini menyumbang 96,63% dari kasus. Fakta bahwa setelah nilai n = 5000 , jumlah kasus penyelesaian masalah konfigurasi tanpa menggunakan prosedur BT secara bertahap menurun, dikaitkan dengan model yang dipilih untuk memilih nilai batas baseLevel2 dan baseLevel3 . Anda dapat mengubah parameter ini dan mencapai peningkatan jumlah solusi tanpa menggunakan prosedur BT. Namun, ini akan mengarah pada peningkatan waktu perhitungan, karena partisipasi blok kelima dalam operasi algoritma akan meningkat.

Histogram dari pembagian waktu . Pada Gambar 10, untuk nilai n = 1000histogram distribusi waktu pengambilan untuk satu juta solusi disajikan. Pandangan yang tidak biasa dari histogram distribusi (yang kemungkinan besar menyerupai siluet malam bangunan tinggi) tidak terkait dengan kesalahan dalam pemilihan panjang atau jumlah interval. Ini adalah sifat alami dari algoritma ini. Untuk memahami,


Gbr. 10. Histogram dari waktu kompilasi komposisi ukuran sewenang-wenang. ( n = 1000 ; ukuran sampel = 1.000.000 )

mengapa histogram memiliki formulir ini, pertimbangkan distribusi waktu pengambilan untuk komposisi yang memiliki ukuran yang sama. Untuk ini, sebagai contoh, dari sampel awal kami akan memilih semua komposisi yang ukurannya 800. Ada 998 komposisi tersebut dalam sampel satu juta. Gambar 11 menunjukkan histogram dari distribusi waktu penghitungan untuk sampel ini. Dapat dilihat dari gambar bahwa distribusi terdiri dari enam histogram terpisah, dengan ukuran yang menurun.


Fig. 11. Histogram waktu kompilasi komposisi dengan ukuran yang sama (k = 800). ( n = 1000 ; ukuran sampel = 998 )

Alasan mengapa waktu kompilasi 998 komposisi, di mana masing-masing 800 ratu didistribusikan secara acak, "dikelompokkan" menjadi 6 kelompok, karena prosedur Pelacakan Kembali digunakan. Histogram pertama pada gambar, dengan ukuran sampel maksimum, adalah solusi memilih di mana prosedur BT tidak pernah digunakan. Ini adalah kelompok solusi tercepat. Histogram kedua, yang secara signifikan lebih kecil dalam ukuran daripada yang pertama, adalah solusi di mana prosedur BT hanya digunakan sekali. Oleh karena itu, waktu keputusan dalam grup ini sedikit lebih lama daripada yang pertama. Dengan demikian, pada kelompok ketiga, prosedur BT digunakan dua kali, pada kelompok keempat - tiga kali, dll., Yaitu Keputusan di mana prosedur BT digunakan berulang kali dilakukan lebih lama. Solusi semacam itu membentuk ekor kanan panjang dari distribusi yang diinginkan.

Solusi Negatif Salah . Jika kita membagi semua komposisi yang mungkin untuk nilai arbitrer dari nke positif dan negatif, maka di antara komposisi positif ada yang algoritma ini dapat diklasifikasikan sebagai negatif. Ini disebabkan oleh kenyataan bahwa, dalam batas yang ditentukan oleh parameter pencarian, algoritma tidak dapat menemukan cara yang tepat untuk menyelesaikan komposisi tersebut. Seperti yang ditunjukkan oleh hasil percobaan (Tabel 2), jumlah kasus seperti itu tidak melebihi 0,0001 dari ukuran sampel, dan nilai kesalahan ini berkurang dengan meningkatnya n . Selain itu, untuk semua nilai n> 800, tidak ada satu pun kasus solusi False Negative . Bahkan meningkatkan ukuran sampel menjadi satu juta untuk n = 1000 tidak menghasilkan False Negativekeputusan. Hasilnya memungkinkan kami untuk merumuskan aturan berikut untuk menyelesaikan masalah: “Setiap komposisi acak k ratu yang didistribusikan secara konsisten pada papan catur acak berukuran nxn dapat diselesaikan hingga solusi lengkap dibuat, atau akan diputuskan bahwa komposisi ini negatif, dan tidak dapat harus diselesaikan. Probabilitas membuat keputusan seperti itu tidak melebihi 0,0001 . Ketika ukuran papan catur meningkat, kemungkinan membuat keputusan yang salah berkurang. Kompleksitas waktu dari algoritma adalah linear. ”

8. Kesimpulan

1. Algoritma disajikan yang memungkinkan, dalam waktu linier, untuk menyelesaikan masalah set lengkap sampai solusi lengkap dari komposisi acak k ratu, secara konsisten didistribusikan pada papan catur ukuran nxn sewenang-wenang . Selain itu, untuk komposisi k ratu ( 1≤ k <n ), solusi diberikan, jika ada, atau keputusan dibuat bahwa komposisi ini tidak dapat diselesaikan. Probabilitas kesalahan dalam membuat keputusan seperti itu tidak melebihi 0,0001, dan nilai ini menurun dengan meningkatnya ukuran papan catur.

2. Pengoperasian algoritma ini didasarkan pada penggunaan dua aturan penting:

a) Pada tahap akhir penyelesaian masalah, dari semua jalur bebas yang tersisa, satu dipilih yang jumlah posisi bebasnya minimal ( aturan risiko minimum ). Ini meminimalkan risiko yang terkait dengan kemungkinan mengecualikan posisi kosong terakhir di beberapa jalur yang tersisa.

b) Dari semua posisi kosong dalam garis yang dipermasalahkan, posisi itu dipilih yang menyebabkan kerusakan minimal pada posisi bebas di garis bebas yang tersisa ( aturan kerusakan minimum ). Yang dimaksud dengan " kerusakan minimal " adalah pemilihan posisi seperti itu dalam garis yang mengecualikan jumlah posisi bebas paling sedikit di semua jalur bebas yang tersisa.

3. Ditetapkan bahwa sebagai hasil dari operasi algoritma ini, waktu rata-rata yang diperlukan untuk ratu untuk ditempatkan pada satu baris berkurang dengan meningkatnya n. Waktu rata-rata yang diperlukan untuk menempatkan ratu pada satu baris dalam kasus ketika n adalah 10 ⁸ adalah 21 kali lebih kecil dari waktu yang sesuai untuk kasus n = 50.

4. Ditemukan bahwa dalam kisaran nilai n = (7, ..., 100000) jumlah solusi di mana prosedur pelacakan Kembali tidak pernah digunakan melebihi 35%. Selain itu, dalam kisaran nilai n = (320, ..., 22500) , jumlah kasus tersebut melebihi 50%, yang menunjukkan efisiensi tinggi dari algoritma ini.

5. Model untuk mengatur prosedur Pelacakan Kembali diusulkan., berdasarkan pemisahan urutan langkah-langkah keputusan di tingkat dasar. Level berarti langkah keputusan tertentu dengan sejumlah ratu yang ditempatkan dengan benar . Rumus regresi diberikan untuk menghitung nilai level dasar kedua dan ketiga tergantung pada n .

6. Hasil analisis komparatif dari dua metode seleksi acak, yang disebut randSet & randSet dan rand & rand , disajikan . Ditemukan bahwa algoritma randSet & randSet cepat tapi kasar. Karena itu, penggunaannya terbatas ketika mencapai tingkat dasar kedua. Setelah itu, rand & rand digunakan., yang dilakukan tidak begitu cepat, tetapi lebih efektif menempatkan ratu di papan catur.

7. Algoritma yang efektif untuk memverifikasi kebenaran solusi n-Queens Problem diberikan . Program ini juga dirancang untuk memverifikasi kebenaran komposisi acak ukuran sewenang-wenang. Program ini bekerja cukup cepat. Misalnya, waktu yang diperlukan untuk memvalidasi solusi yang terdiri dari 5 juta posisi adalah 0,85 detik.

9. Komentar

1. Seperti yang ditunjukkan pada awal artikel, penelitian dilakukan dalam kisaran nilai n , dari 7 hingga 100 juta. Namun, program ini diuji dalam rentang nilai n yang lebih luas , hingga satu miliar. Benar, dalam kasus terakhir, program harus sedikit disesuaikan, mengingat ukuran array yang besar. Oleh karena itu, jika ukuran RAM memungkinkan, maka dimungkinkan untuk melakukan perhitungan untuk nilai n yang besar.

2. Nilai-nilai indikator dasar, serta nilai batas jumlah pengulangan di berbagai tingkat, dioptimalkan untuk menyelesaikan masalah dalam seluruh rentang penelitian. Mereka dapat diubah dalam rentang yang lebih kecil dan mengurangi waktu penghitungan. Penting untuk tidak meningkatkan pangsa solusi Negatif Palsu .

3. Pada artikel ini, saya menggunakan waktu keystroke Masukkan sebagai semacam ukuran waktu untuk menilai seberapa cepat algoritma bekerja. Jika hasilnya muncul segera setelah menekan tombol, maka pada tingkat persepsi pengguna tampaknya program bekerja "sangat" cepat. Tidak peduli seberapa cepat algoritma ini bekerja, hasilnya tidak akan muncul di layar sampai kunci selesai. Oleh karena itu, bagi saya tampak bahwa ukuran waktu yang kondisional dapat berfungsi sebagai tingkat ambang batas untuk tidak secara ketat membandingkan kecepatan berbagai algoritma.

4. Filosofis ... Selama penelitian, sejumlah besar publikasi yang terkait dengan solusi masalah non-deterministik dipertimbangkan. Dalam kebanyakan kasus, ini adalah tugas di mana perlu untuk membuat pilihan di ruang besar negara di bawah ketentuan pembatasan yang diberikan. Membandingkan mereka, itu menarik untuk mengetahui sejauh mana seseorang dapat maju dalam memecahkan masalah seperti itu menggunakan pendekatan matematika standar. Saya mendapat kesan bahwa tidak mungkin menyelesaikan masalah seperti itu hanya berdasarkan definisi, pernyataan lemma dan bukti teorema. Tampak bagi saya bahwa untuk menyelesaikan masalah seperti itu perlu menggunakan metode matematika algoritmik menggunakan simulasi komputer. Untuk menunjukkan validitas kesimpulan ini, sebagai contoh sederhana, saya menyiapkan papan catur yang ukurannya 10⁹ x 10 ⁹ dua komposisi dengan ukuran yang sama, terdiri dari 999.999.482 ratu. Mereka disiapkan seperti yang dijelaskan di awal artikel dan disajikan sebagai dua file dalam format .mat. Mereka dapat diunduh di tautan ini (Dua file uji) . File cukup "berat", ukuran masing-masing adalah sekitar 3,97 Gb. Dalam 999 997 976 baris (dalam 99,9998% kasus) posisi ratu di kedua komposisi bertepatan, dan hanya dalam 1506 garis sewenang-wenang posisi ratu berbeda.

Untuk melengkapi data komposisi ke solusi lengkap, Anda perlu menempatkan ratu dengan benar di 518 baris bebas yang tersisa. Jumlah cara yang mungkin untuk mengatur 518 ratu di jalur bebas yang tersisa (dengan mempertimbangkan hanya jumlah cara untuk memilih posisi bebas di jalur yang dipilih) adalah sekitar 10 ¹⁴⁶⁶. Perbedaan antara kedua komposisi ini hanya bahwa salah satu dari mereka adalah positif dan dapat diselesaikan sampai solusi lengkap, dan komposisi lainnya negatif - tidak dapat diselesaikan sampai solusi lengkap. Pertanyaan: "Apakah mungkin, berdasarkan pendekatan matematis yang ketat (yaitu, tanpa melakukan operasi komputasi algoritmik), untuk menentukan mana dari dua komposisi ini yang positif?" Jika ini tidak mungkin diselesaikan, maka kita dapat mengasumsikan bahwa proposisi yang dibuat terbukti dengan kontradiksi.

Saya ingin mencatat bahwa apa pun pendekatan terhadap solusi matematis ketat untuk masalah ini, perlu untuk menentukan status 518 * 10 ⁹sel di baris bebas yang tersisa. Untuk melakukan ini, perlu untuk mempertimbangkan setiap posisi ratu yang didirikan sebelumnya, dan ada hampir satu miliar dari mereka, untuk menetapkan batasan yang masing-masing ratu yang didirikan memaksakan pada posisi bebas di 518 baris yang tersisa. Saya tidak menemukan "titik tumpu" yang memungkinkan saya melakukan pekerjaan ini hanya berdasarkan pendekatan matematis yang ketat, tanpa perhitungan algoritmik.

Di sini saya telah memberikan contoh minimal yang hanya terdiri dari dua komposisi. Jika perlu, jumlah komposisi tersebut dapat ditingkatkan.

Perlu dicatat bahwa berdasarkan algoritma linear yang diusulkan, sedikit disesuaikan untuk bekerja dengan komposisi besar, tugas-tugas yang mana dari dua komposisi uji dapat diselesaikan sampai solusi lengkap dilakukan pada desktop-13 , dalam waktu sekitar 4,5 menit (tidak termasuk waktu pemuatan data input).

10. Penambahan

Tindakan para profesor yang merekomendasikan tugas-tugas yang mampu bagi siswa untuk dikembangkan dan diteliti layak dihargai. Ini membutuhkan upaya yang cukup besar, tetapi mengatasi kesulitan, peneliti melihat tugas kompleks lainnya secara berbeda. Saya pikir akan bermanfaat untuk memperluas opsi untuk mengatur Masalah n-Queens untuk tujuan tersebut. Jika Anda melihat tugas yang sama dari perspektif yang berbeda, Anda dapat melihat berbagai hal. Berikut adalah beberapa di antaranya.

1. Pertimbangkan masalah mengatur n ratu di papan "catur" persegi panjang berukuran nxm . Nyatakan k = m - n . Biarkan beberapa solusi diperoleh, dan di masing-masing nAda satu ratu di setiap baris. Kami mengecualikan posisi tersebut di mana ratu berada dari pertimbangan lebih lanjut. Sekarang di setiap baris ada posisi bebas m-1 . Dalam posisi bebas yang tersisa, kami kembali menemukan satu solusi. Seperti sebelumnya, kami mengecualikan dari pertimbangan lebih lanjut posisi di mana ratu dari solusi kedua berada. Sekarang di setiap baris ada m-2 posisi bebas. Jelas, solusi pertama dan kedua tidak berpotongan di posisi mereka di baris mana pun - mereka ortogonal. Diperlukan untuk menentukan jumlah maksimum solusi saling ortogonal untuk berbagai nilai k . Jika n saling solusi ortogonal ditemukan untuk nilai k = 0maka Royal Latin Square akan dibangun.

Komentar . Kertas Grigoryan E. (2018) telah menunjukkan bahwa untuk setiap solusi n-Queens ada solusi yang saling melengkapi, yang tidak mengganggu itu. Ini berarti bahwa untuk nilai arbitrer n , himpunan semua solusi Masalah n-Queens dibagi menjadi dua himpunan bagian berukuran sama . Solusi apa pun dari subset kedua adalah solusi pelengkap untuk solusi yang sesuai dari subset pertama. Aturannya cukup sederhana, jika Q1 (i) adalah solusi dari set pertama, maka solusi komplementer yang sesuai Q2 (i)dari subset kedua ditentukan oleh rumus Q2 (i) = n + 1 - Q1 (i), di mana i = (1, ..., n) . Aturan inilah yang menjelaskan fakta bahwa jumlah semua solusi dari Masalah n-Queens , untuk nilai sewenang-wenang n , selalu merupakan bilangan genap. (Aturan ini memungkinkan kita untuk mengurangi separuh waktu untuk menghitung semua solusi lengkap untuk ukuran n sembarang dari papan catur. Jika kita menyatakan dengan 2 * k jumlah total semua solusi, maka nilai k sama dengan indeks dalam daftar berurutan semua solusi ketika Q (k) + Q ( k + 1) = n + 1 ).

2. Dalam rumusan awal masalah Masalah n-Qeens , setelah ratu ditempatkan pada posisi (i, j), tindakan berikut dilakukan:

a) semua sel baris i dan kolom j

dikecualikan; b) semua sel yang terletak di garis diagonal kiri dan kanan yang melewati sel (i, j) dikecualikan .

Kami mengubah kondisi b) dalam pernyataan masalah. Alih-alih menghilangkan sel, kita akan menggunakan switching sel. Jika sel yang terletak di garis diagonal kiri atau kanan bebas, maka kita akan menutupnya, jika sel ditutup, maka kita akan membukanya. Ini membuatnya lebih mudah untuk menemukan solusi. Namun, alih-alih matriks kuadrat nxn , kami menganggap matriks persegi panjang dengan ukuran nx (n - k) . Diperlukan, untuk nilai n yang diberikan , untuk menemukan nilai maksimum kdi mana setidaknya tiga solusi ortogonal dapat diperoleh. Bagaimana nilai k berubah dengan meningkatnya nilai n ?

3. Ubah beberapa kondisi dalam formulasi awal masalah Masalah n-Queens . Ketika ratu diposisikan pada posisi (i, j) pada papan catur berukuran nxn :

a) kita mengecualikan semua sel dalam baris i ,

b) jika indeks j adalah bilangan genap, maka:

b1) kita mengecualikan sel dalam baris genap j,

b2) kita mengecualikan sel dalam garis genap yang memotong diagonal kiri dan kanan melewati sel (i, j) ,

c) Jika indeks jangka ganjil, maka item b1) dan b2) dipenuhi untuk sel yang terletak pada garis ganjil.

3.1 Telah diketahui (Sloane-2016) bahwa daftar nilai semua solusi dari Masalah nQueens , untuk n = (8, 9, 10, 11, 12, 13, 14, 15, 16) , masing-masing, adalah (92, 352, 724, 2680, 14200, 73712, 365596, 2279184, 14772512) . Bagaimana jumlah semua solusi berubah jika, dalam pernyataan masalah, kondisi standar untuk pengecualian diagonal diubah menjadi paragraf b) atau paragraf c)?

3.2 Diketahui oleh Grigoryan (2018) bahwa jika kita menentukan frekuensi partisipasi sel-sel yang berbeda dari matriks solusi dalam pembentukan daftar semua solusi, kita dapat menemukan bahwa ada hubungan yang harmonis antara semua sel dalam bentuk simetri vertikal dan horizontal dari frekuensi yang sesuai. Ini berarti bahwa jika kita mengasumsikan bahwa k <n / 2 , maka frekuensi sel-sel dari baris k-th akan identik dengan frekuensi sel-sel dari baris n-k + 1 . Demikian pula, frekuensi sel kolom k-th akan identik dengan frekuensi sel kolom n-k + 1 . Pertanyaan: "Bagaimana hubungan harmonis ini berubah dalam konteks tugas?"

4. Semua sel papan catur dibagi menjadi dua kelas berdasarkan warnanya. Diyakini bahwa satu warna putih, yang lain hitam. Pertimbangkan dua papan catur dan letakkan salah satunya di sisi yang lain sehingga ujungnya benar-benar bertepatan. Hasilnya, kami mendapatkan "sandwich" dari dua papan catur, di mana pengaturan sel putih dan hitam bertepatan. Tugasnya adalah untuk menemukan solusi secara bersamaan pada dua papan, mengamati kondisi berikut:

a) Jika pada salah satu papan ratu berada pada sel hitam dengan indeks (i, j) , maka:

- pada kedua papan semua sel hitam yang terjadi pada baris i dan kolom j ,

- pada kedua papan semua sel hitam yang terletak di sepanjang diagonal kiri dan kanan yang melewati sel (i, j) dikecualikan .

b) Jika pada salah satu papan ratu terletak pada sel putih dengan indeks (i, j) , maka semua tindakan paragraf a) dilakukan hanya untuk sel putih.

5. Bayangkan bahwa dalam matriks solusi ukuran nxn , baris dapat bergeser relatif satu sama lain ke kanan atau kiri, dengan langkah sel k . Selain itu, jika baris sebelumnya digeser, misalnya, ke kiri, maka baris berikutnya harus digeser ke kanan, mis. setiap baris berikutnya digeser ke arah yang berlawanan dengan baris sebelumnya. Sebagai hasil dari konstruksi ini, kami memperoleh matriks ukuran persegi panjangnx (n + k) , di mana di setiap baris k sel dari awal baris atau dari akhir akan dikecualikan dari pertimbangan. Tugasnya adalah menemukan nilai maksimum k untuk nilai arbitrer n yang setidaknya ada satu solusi n-Queens Problem . Pertimbangkan varian masalah di mana offset satu baris terhadap yang lain adalah bilangan acak mulai dari k1 hingga k2 . 6. Formulasi satu- dimensi dari Masalah nQueens . Biarkan n segmen dengan panjang sewenang-wenang, yang dinomori dari 1 hingga n , diletakkan pada setengah-sumbu . Bagilah setiap segmen dengan n


sel dengan ukuran acak, dan dalam setiap segmen, jumlah sel dari 1 hingga n . Kami menyebut sel tersebut terbuka. Hal ini membutuhkan dekat satu sel pada setiap segmen, mengingat keterbatasan berikut:

a) Kita bisa memilih sel terbuka dengan indeks j dari i segmen th jika:

D1 (r) = 0;

D2 (t) = 0;

di mana r = n + j - i, t = j + i, D1 dan D2 adalah array kontrol satu dimensi yang terdiri dari 2n sel yang sebelumnya nol.

b) Setelah pilihan ini, segmen i dan sel dengan nomor j akan ditutupdi semua segmen gratis yang tersisa. Juga diperlukan untuk menutup sel yang sesuai dalam array kontrol:

D1 (r) = 1;

D2 (t) = 1;

Dalam pengaturan ini, tugas benar-benar identik dengan yang asli. Yang menarik adalah rumusan masalah ini dengan kondisi kendala lainnya. Misalnya, jika bukan rumus:
r = n + j - i, t = j + i, ,
akan dipertimbangkan rasio lainnya, yang secara fungsional terkait indeks r dan t indeks (i, j) membuat matriks.

7. Kata-kata tugas berdasarkan guci dengan bola (identik dengan kata-kata sebelumnya). Misalkan ada n guci bernomor dari 1 ke n, dan di setiap guci ada n bola, juga dinomori dari 1 hingga n . Membutuhkan guci jauh dari masing-masing bola, mengingat keterbatasan berikut:

a) kita dapat memilih balon dengan jumlah j dari i urn th jika:

D1 (r) = 0 ,

D2 (t) = 0 ,

di mana r = n + j - i, t = j + i, D1 dan D2 adalah array kontrol satu dimensi yang terdiri dari 2n sel yang sebelumnya nol.

b) Setelah pilihan ini, kotak suara i dan bola dengan nomor j akan ditutup di semua kotak suara gratis yang tersisa. Penting juga untuk menutup sel yang sesuai dalam array kontrol:

D1 (r) = 1 ,

D2 (t) = 1 .

Dalam pengaturan ini, tugas benar-benar identik dengan yang asli. Seperti dalam kasus sebelumnya, pernyataan masalah ini dengan kondisi lain yang secara fungsional menghubungkan indeks r dan t dengan indeks (i, j) dari matriks keputusan adalah menarik .

8. Permainan . Pertimbangkan papan catur berukuran nxn . Mari kita kembali warna ke ratu, biarkan beberapa ratu memiliki warna putih, yang lain hitam. Kami juga mengembalikan warna putih dan hitam bolak-balik ke sel-sel papan catur, berdasarkan fakta bahwa sel dengan indeks (1, n)harus putih. Semua sel di awal permainan dianggap gratis. Ratu putih membuat langkah pertama. Pemain menempatkan ratu dalam sel bebas sewenang-wenang dengan indeks (i, j) . Biarkan itu menjadi sel putih. Sebagai hasil dari pilihan ini, mereka ditutup:

a) semua sel putih baris i ,

b) semua sel putih kolom j ,

c) semua sel putih yang terletak di diagonal kiri dan kanan melewati sel (i, j) .

Jika sel (i, j) berubah menjadi hitam, maka semua poin (a, b, c) terpenuhi, dan karenanya, semua sel warna hitam ditutup. Selanjutnya, Black melakukan gerakan, menempatkan ratu di salah satu sel bebas yang tersisa. Setelah itu, dengan cara yang sama, sel-sel menutup, seperti dijelaskan di atas. Waktu untuk memikirkan langkah selanjutnya sudah ditentukan, dan dipilih berdasarkan persetujuan para pihak. Jika selama waktu yang ditentukan, salah satu pemain tidak menyelesaikan langkahnya, maka permainan akan ditransfer ke yang lain. Permainan berakhir jika kedua pemain, satu demi satu, gagal menyelesaikan giliran mereka dalam waktu yang ditentukan. Orang yang bisa menempatkan lebih banyak ratu di papan menang.

9. Tentang stabilitas pemilihan acak. Pertimbangkan model randSet & randSet . Sebagai hasil dari membandingkan n pasangan acak dari indeks baris dan kolom, pada tahap pertama siklus, adalah mungkin untuk menetapkan ratu rata-rata dik * n baris. Nilai k dapat dianggap sebagai nilai konstan sama dengan 0,6. Nilainya bervariasi dari 0,605701 pada n = 10 , dan hingga 0,599777, pada n = 10 ⁶ , dan, dengan meningkatnya n , varian nilai ini menurun. Apa alasan untuk "keteguhan" seperti itu? Mengapa, dengan pemilihan acak indeks baris dan indeks posisi ratu di baris ini, atas dasar dua daftar angka yang diperoleh atas dasar permutasi acak angka dari 1 hingga n, dimungkinkan untuk secara konsisten menempatkan ratu (rata-rata) pada 60% garis?

10. Biarkan ukuran papan catur menjadi nxn . Berdasarkan prosedur randSet & randSetletakkan ratu di papan catur sampai cabang pencarian menemui jalan buntu. Nyatakan panjang komposisi yang diperoleh k . Jika, untuk nilai n yang diberikan , ulangi prosedur ini berkali-kali, dan buat histogram dari distribusi nilai k , ternyata perubahan frekuensi kejadian peristiwa dengan nilai mode distribusi berbeda dari perubahan frekuensi kemunculan peristiwa setelah nilai ini. Jika, berdasarkan nilai modal, histogram dibagi menjadi dua bagian, maka bagian kiri tidak akan bertepatan dengan bagian kanan. Pola ini adalah karakteristik untuk nilai n. Mengapa, setelah transisi panjang komposisi melalui nilai modal, apakah frekuensi timbulnya peristiwa mengambil bentuk yang berbeda? Yang dimaksud dengan suatu peristiwa, yang kami maksud adalah menerima komposisi dengan ukuran tertentu, sebelum mencapai tingkat kemandekan.

Sastra

1. Nauck, F. (1850). Briefwechsel mit allen fur alle . Illustrierte Zeitung, 15, 182.

2. Gent, IP, Jefferson, C. & Nightingale, P. (2017). Kompleksitas penyelesaian n-Queens ,
Jurnal Penelitian Kecerdasan Buatan., 59, 815-848.

3. Sosic, R., & Gu, J. (1990). Algoritma waktu polinomial untuk masalah n-queens . Buletin SIGART, 1 (3), 7–11.

4. Richards, M. (1997). Algoritma backtracking di MCPL menggunakan pola bit dan rekursi .
Tech. rep., Laboratorium Komputer, Universitas Cambridge.

5. Metode Pengacakan dalam Desain Algoritma, Prosiding Lokakarya DIMACS, Princeton, New Jersey, AS, 12-14 Desember 1997. Seri DIMACS dalam Matematika Diskrit dan Ilmu Komputer Teoretis 43, DIMACS / AMS 1999, ISBN 978-0-8218-0916-7

6. Grigoryan E. (2018). Investigasi Keteraturan dalam Pembentukan Solusi Masalah n-Queens . Modeling of Artificial Intelligence, 5 (1), 3-21

7. Sloane N.-JA (2016). Ensiklopedia on-line dari urutan bilangan bulat.