Bidang logis dalam database, apakah ada penangkal?

Seringkali tabel berisi sejumlah besar bidang logis, tidak ada cara untuk mengindeks semuanya, dan efektivitas pengindeksan seperti itu rendah. Namun demikian, untuk bekerja dengan ekspresi logis sewenang-wenang dalam SQL, mekanisme pengindeksan multidimensi cocok, yang akan dibahas di bawah cat.

Dalam SQL, bidang logis digunakan terutama dalam dua kasus. Pertama, ketika Anda benar-benar membutuhkan atribut biner, misalnya, 'beli / jual' di tabel transaksi. Atribut seperti itu jarang berubah seiring waktu.

Kedua, untuk merekam keadaan mesin negara yang menggambarkan catatan. Dipahami bahwa objek logis yang berhubungan dengan catatan tabel melewati serangkaian keadaan, jumlah yang dan transisi di antara mereka ditentukan oleh logika yang diterapkan. Contoh sederhana adalah teknik "hapus lunak", ketika catatan tidak secara fisik dihancurkan, tetapi hanya ditandai sebagai dihapus.

Jika mesinnya kompleks, mungkin ada cukup banyak bidang seperti itu, di salah satu tabel kami ada 58 (+14 ketinggalan zaman) bidang tersebut (termasuk set bendera) dan ini bukan sesuatu yang luar biasa. Ini pada awalnya tidak dimaksudkan, tetapi ketika produk berkembang dan persyaratan eksternal berubah, mesin yang sesuai berkembang, pengembang datang dan pergi, analis berubah ... pada titik tertentu mungkin lebih aman untuk mendapatkan bendera baru daripada memahami semua seluk-beluk. Selain itu, data historis telah terakumulasi dan kondisinya harus tetap memadai.


Menempatkan bendera berarti tidak hanya menambahkan bidang dari jenis yang sesuai, tetapi juga memperhitungkannya dalam pengoperasian automaton, kondisi apa yang memengaruhinya, di mana transisi yang dilibatkannya. Dalam praktiknya, tampilannya seperti ini:

• suatu proses atau serangkaian proses, sebut saja mereka "penulis", buat catatan baru di kondisi awal (mungkin di salah satu kondisi awal)
• sejumlah proses, sebut saja mereka "pembaca", dari waktu ke waktu mereka membaca objek yang ada di negara yang mereka butuhkan
• sejumlah proses, sebut saja "penangan", pantau status spesifik dan, berdasarkan logika yang diterapkan, ubah status ini. Yaitu mengoperasikan mesin negara.

Untuk memilih catatan yang berada dalam kondisi tertentu, cukup jarang bila pemfilteran oleh salah satu bidang Boolean sudah cukup. Biasanya ini adalah ekspresi keseluruhan, terkadang non-sepele. Tampaknya Anda perlu mengindeks bidang ini dan prosesor SQL akan mengetahuinya. Tapi tidak sesederhana itu.

Pertama, bisa ada banyak bidang Boolean, mengindeks semuanya akan terlalu boros.

Kedua, itu bisa berubah menjadi tidak berguna sejak itu selektivitas untuk masing-masing bidang akan rendah, dan probabilitas gabungan tidak tercakup oleh statistik prosesor SQL.

Misalkan dalam tabel T1 ada dua bidang Boolean: F1 & F2, dan kueri

select F1, F2, count(1) from T1 group by F1, F2 

memberi

Yaitu meskipun, menurut F1 & F2, benar dan salah sama-sama memungkinkan, kombinasi (benar, salah) hanya keluar sekali dari seribu. Akibatnya, jika kita mengindeks F1 & F2 secara terpisah dan memaksanya untuk digunakan dalam kueri , prosesor SQL harus membaca setengah dari kedua indeks dan melewati hasilnya. Mungkin lebih murah untuk membaca seluruh tabel dan menghitung ekspresi untuk setiap baris.

Dan bahkan jika Anda mengumpulkan statistik pada permintaan yang sudah selesai, itu tidak akan banyak berguna. statistik khusus untuk bidang yang bertanggung jawab untuk keadaan mesin mengapung sangat banyak. Memang, setiap saat "penangan" dapat datang dan mentransfer setengah dari garis S1 negara ke S2.

Untuk bekerja dengan ekspresi seperti itu, indeks multidimensi menunjukkan dirinya, algoritma yang disajikan sebelumnya dan terbukti cukup baik.

Tetapi pertama-tama Anda perlu mencari tahu bagaimana ekspresi logis sewenang-wenang akan berubah menjadi permintaan untuk indeks.

Bentuk normal disjungtif

Kueri tunggal ke indeks multidimensi adalah persegi panjang multidimensi yang membatasi ruang kueri. Jika bidang berpartisipasi dalam permintaan, batasan ditetapkan untuk itu. Jika tidak, persegi panjang dalam koordinat ini hanya dibatasi oleh lebar koordinat ini. Koordinat logis memiliki kapasitas 1.

Kueri pencarian dalam indeks tersebut adalah rantai & (kata hubung), misalnya, ekspresi: v1 & v2 & v3 & (! V4), setara dengan v1: [1,1], v2: [1,1], v3: [1, 1], v4: [0,0]. Dan semua bidang lainnya memiliki rentang: [0,1].

Mengingat hal ini, pandangan kami segera beralih ke DNF - salah satu bentuk kanonik dari ekspresi logis. Dikatakan bahwa ungkapan apa pun dapat diwakili sebagai disjungsi dari konjungsi sastra. Literal di sini mengacu pada bidang logis atau negasinya.

Dengan kata lain, melalui manipulasi sederhana, ekspresi logis apa pun dapat direpresentasikan sebagai disjungsi dari beberapa pertanyaan ke indeks logis multidimensi.

Ada satu NAMUN. Transformasi semacam itu dalam beberapa kasus dapat menyebabkan peningkatan ukuran ekspresi yang eksponensial. Misalnya, konversi dari



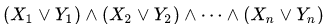
mengarah ke ekspresi 2 ** n istilah. Dalam kasus seperti itu, pengembang aplikasi harus memikirkan makna fisik dari apa yang dia lakukan, dan pada bagian dari prosesor SQL, Anda selalu dapat menolak untuk menggunakan indeks logis jika jumlah konjungsi melebihi batas yang wajar.

Algoritma Pengindeksan Multidimensi

Untuk pengindeksan multidimensi, sifat-sifat kurva penomoran yang mirip sendiri berdasarkan pada simpleks hiper-kubik dengan sisi 2. Digunakan , ternyata , dua versi kurva tersebut sangat penting secara praktis - kurva Z dan kurva Hilbert.


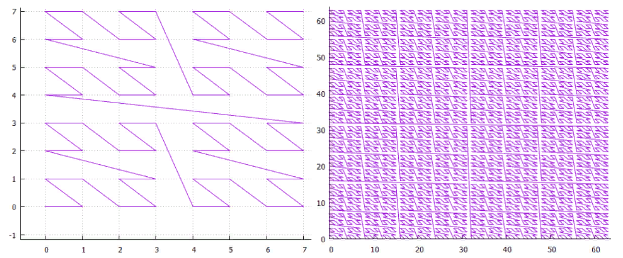Gambar 1 kurva Z dua dimensi, iterasi 3 dan 6


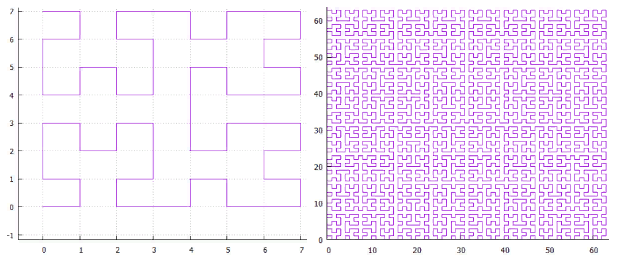Gambar 2 kurva Hilbert dua dimensi, iterasi 3 dan 6

• Simpleks N-dimensi dengan sisi 2 memiliki 2 simpul ** ** dan (2 ** n-1) transisi di antaranya.
• Iterasi dasar simpleks mengubah setiap simpul simpleks menjadi simpleks level bawah.
• Setelah melakukan jumlah iterasi yang diperlukan, kita dapat membuat kisi hiper-kubik dengan berbagai ukuran.
• Selain itu, setiap simpul kisi ini akan memiliki nomor uniknya sendiri - jalur yang diambil sepanjang kurva penomoran sejak awal. Selain itu, setiap node kisi ini memiliki nilai di setiap koordinat. Faktanya, kurva penomoran menerjemahkan titik multidimensi menjadi nilai satu dimensi yang cocok untuk pengindeksan dengan B-tree reguler .
• Semua node yang terletak di dalam simpleks level apa pun berada dalam interval yang sama dan interval ini tidak bersinggungan dengan simpleks apa pun dari level yang sama.
• Oleh karena itu, kotak pencarian (kotak) apa pun dapat dibagi menjadi sejumlah kecil subqueries hiper-kubik, di mana masing-masing indeks dapat dibaca oleh satu pencarian / lintasan.
  
• Untuk ini kami menambahkan keajaiban pekerjaan tingkat rendah dengan B-tree agar tidak membuat permintaan yang tidak berguna dan ... algoritma siap.

Begini cara kerjanya dalam praktik:


Gambar 3 Contoh pencarian dalam indeks dua dimensi (kurva-Z)

Gambar 3 menunjukkan pembagian tingkat pencarian asli ke dalam sub-kueri dan poin yang ditemukan. Indeks dua dimensi digunakan, dibangun di atas serangkaian 100.000.000 titik acak yang terdistribusi secara seragam [1.000.000, 1.000.000].

Indeks multidimensi logis

Karena kita berbicara tentang pengindeksan multidimensi, sekarang saatnya untuk memikirkan berapa multidimensi itu? Apakah ada batasan objektif?

Tentu saja, karena B-tree memiliki organisasi halaman dan untuk menjadi pohon, setidaknya dua elemen harus dijamin agar sesuai pada halaman. Jika Anda mengambil halaman untuk 8K, maka menyimpan satu item tidak bisa lebih dari 4K. Dalam 4K, tanpa kompresi, sekitar 1000 nilai 32-bit cocok. Ini cukup banyak, di luar batas aplikasi yang masuk akal, kita dapat mengatakan bahwa batas fisik praktis tidak tersedia.

Ada sisi lain, setiap dimensi tambahan sama sekali tidak gratis, ini memakan ruang disk dan memperlambat pekerjaan. Dari sudut pandang "makna fisik", bidang yang berubah pada saat yang sama harus dimasukkan dalam indeks yang sama dan pencarian untuk mereka juga berjalan bersamaan. Tidak ada gunanya mengindeks semuanya dalam satu baris.

Bidang logis berbeda. Seperti yang telah kita lihat, lusinan bidang logis dapat dilibatkan dalam mekanisme yang sama. Dan biaya penyimpanan / membaca cukup kecil. Ada godaan untuk mengumpulkan semua bidang logis dalam satu indeks dan melihat apa yang terjadi.

Benar, ada nuansa:

• Sampai sekarang, dalam nilai yang diindeks, angka-angka dari koordinat yang berbeda dicampur, dalam angka-angka paling penting dari kunci adalah bit-bit paling tidak signifikan dari koordinat ... Oleh karena itu, urutan bidang selama pengindeksan tidak menjadi masalah.
• Sekarang, satu bit dihabiskan untuk menyimpan nilai satu bidang logis. Yaitu beberapa bidang logis akan menuju ke akhir kunci, dan beberapa ke awal. Ini berarti bahwa pemfilteran sebagian bidang akan sangat efektif, dan sebagian akan sangat tidak efisien. Bahkan, jika kita melakukan pencarian dalam urutan terendah, kita harus membaca seluruh indeks untuk mendapatkan jawaban. Tapi ini (kemungkinan besar) lebih baik daripada membaca seluruh tabel untuk menjawab pertanyaan yang sama.
• Ada masalah pilihan - semua bidang logis sama, tetapi beberapa akan lebih sama daripada yang lain. Dari pertimbangan umum, perlu untuk melihat distorsi statistik, semakin kuat rasio benar / salah untuk bidang tertentu jauh dari kesetimbangan, semakin tua harus menjadi debit di mana nilainya muncul.
• Pemartisian berdasarkan jenis kurva penomoran menghilang, jika sebelumnya perlu memilih antara kurva Z dan kurva Hilbert, tidak ada perbedaan praktis pada data bit tunggal.
• NULLs. Berdasarkan fakta bahwa NULL bukan nilai yang tidak diketahui, tetapi tidak adanya nilai apa pun, catatan tersebut tidak boleh dimasukkan dalam indeks. Dalam indeks satu dimensi, inilah yang terjadi. Tetapi dalam kasus kami, mungkin ternyata beberapa bidang logis berisi nilai, dan beberapa tidak. Akibatnya, kami tidak dapat memasukkan ini ke dalam indeks sejak saat itu algoritma pencarian tidak tahu cara bekerja dengan logika ternary. Dan oleh karena itu, catatan seperti itu seharusnya tidak mungkin untuk dimasukkan ke dalam tabel (jika ada indeks multidimensi, tidak harus yang logis, omong-omong)

Diharapkan bahwa indeks multidimensi logis dalam beberapa kasus mungkin tidak bekerja dengan sangat efisien. Sebenarnya, indeks apa pun dapat bekerja secara tidak efisien jika terlalu banyak data masuk ke area pencarian. Tetapi untuk indeks multi-dimensi yang logis, ini diperparah dengan ketergantungan pada urutan bidang yang dijelaskan di atas, ketika demi hasil kecil Anda harus membaca seluruh indeks. Sejauh ini merupakan masalah dalam praktiknya, hanya eksperimen yang dapat ditampilkan.

Eksperimen numerik

Membangun indeks:

• indeks akan menjadi 128-bit yaitu dibangun di 128 bidang logis
• dan akan mengandung 2 ** 30 elemen
• nilai elemen indeks akan menjadi angka dari 0 hingga 2 ** 30
• kunci elemen indeks akan menjadi nomor yang sama bergeser 48 bit ke kiri, mis. bidang logis 48 hingga 78 akan diisi dengan angka angka dalam urutan yang sama
• sebagai hasilnya, kita mendapatkan 30 bidang logis yang signifikan di tengah kunci, bit yang tersisa akan diisi 0
  
• Setiap bidang boolean memiliki statistik yang sama benar / salah
• Semuanya independen secara statistik.

Cari:

• Setiap percobaan sesuai dengan pemilihan beberapa bidang logis berturut-turut dan penetapan nilai pencarian untuk mereka. Bukan karena algoritme hanya dapat mencari dalam garis, tetapi karena dimungkinkan untuk memvisualisasikan hasil percobaan lebih jelas, kami hanya memiliki dua dimensi - lebar strip dan posisinya
• Sebanyak 24 seri percobaan. Di setiap seri kita akan mencari nilai di mana strip bidang logis dari lebar N yang sesuai (dari 1 hingga 24 bit) menjadikan nilai tersebut benar.
• Di setiap seri akan ada subseries percobaan di mana satu strip bidang logis dari lebar yang dipilih terletak dengan pergeseran S yang berbeda dari awal strip menjadi 30 bidang logis yang signifikan. Total (30-N) percobaan di subseries.
• Di setiap percobaan, pencarian dilakukan untuk semua elemen indeks yang memenuhi kondisi, yaitu bidang dengan angka dalam interval [48 + S, 48 + S + N -1] akan dicari dalam interval [1,1], sisanya dalam interval [0,1]
  
• Pencarian dilakukan dari awal yang dingin
• Hasilnya adalah jumlah halaman disk yang dibaca, termasuk caching (4096 halaman cache)
• Kontrol operasi yang benar dilakukan dengan dua cara - jumlah elemen yang ditemukan harus sama dengan 2 ** (30-N) dan dalam nilai yang ditemukan Anda dapat memeriksa digit yang sesuai
  

Jadi


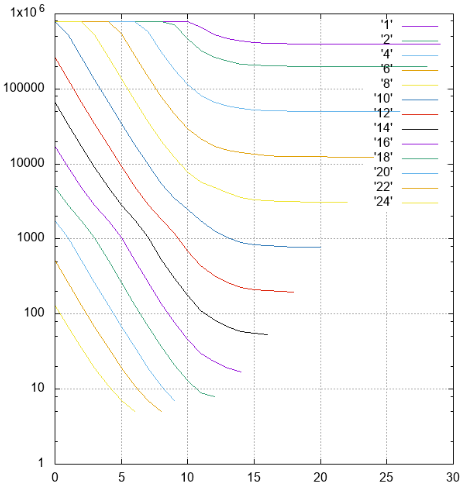Gambar 4 Hasil, jumlah halaman yang dibaca dalam seri berbeda

By Y - jumlah halaman yang dibaca ditunda.
Pada X - pengalihan strip dari kategori termuda (48) ke senior. Garis-garis dengan lebar berbeda ditandatangani dan ditandai dengan warna berbeda.


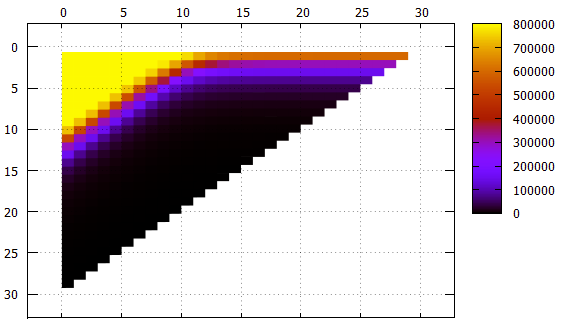Gambar 5 Data yang sama seperti Gambar 4, tampilan lain

Pergeseran X-band
Y - bandwidth

Apa yang harus diperhatikan:

• Meskipun ini tidak langsung terlihat dalam gambar, indeks berfungsi dengan benar, itu terlihat baik dalam jumlah elemen yang ditemukan maupun dalam konten elemen itu sendiri.
• semua garis dengan lebar tidak lebih dari 10 dengan pergeseran 0 memerlukan pembacaan indeks yang berkelanjutan
• garis-garis dengan lebar 1 hingga 18 dengan peningkatan pergeseran mencapai asimtot 2 ** (- N) dari ukuran seluruh indeks, yang logis
• untuk pita yang lebih lebar dari asymptote - ketinggian pohon, tidak boleh ada sedikit bacaan
• sedikit lebih dari 1000 elemen ditempatkan pada halaman lembar indeks, ini dapat dilihat pada strip lebar 10, yang ketika menggeser 0 tidak lagi membutuhkan membaca seluruh indeks, beberapa halaman dapat dilewati
• penyaringan tingkat rendah bekerja sangat baik. Pertimbangkan strip dengan lebar 10. Pilihan pencarian yang ideal adalah dengan pergeseran 20 (total 30 bidang signifikan), ketika tidak ada bidang yang tidak ditentukan dalam awalan sama sekali, data dapat ditemukan dengan satu balok. Dalam situasi ini, sekitar 1/1000 indeks dibaca selama pencarian - 779 halaman.
  Kasus menengah adalah pergeseran 10, kami memiliki awalan dan akhiran dari 10 bidang yang tidak diketahui. Jumlah halaman adalah 2484, hanya tiga kali lebih buruk daripada dalam kasus yang ideal.
  Dan bahkan dalam kasus terburuk, dengan pergeseran 0 (awalan 20 bidang yang tidak diketahui), Anda dapat melewati beberapa halaman.

Secara keseluruhan, algoritma pengindeksan multidimensi dapat dikenali sebagai efisien bahkan dalam kasus yang absurd. Tetapi opsi yang paling tidak berhasil dari sudut pandang indeks logis dipertimbangkan - keadaan yang dapat disetel dalam semua bidang logis independen.

Eksperimen dengan data nyata

Tabel perdagangan , total 278.479.918 baris, data dari salah satu loop tes.
Hasil beberapa kueri dalam tabel di bawah:


Membaca / memproses satu halaman membutuhkan rata-rata 0,8 ms.

Tidak perlu mendeskripsikan arti dari pertanyaan spesifik, mereka di sini hanya untuk menunjukkan operabilitas. Omong-omong, yang dikonfirmasi.

Tetapi sebelum teknik ini dapat digunakan secara praktis, masih banyak yang harus dilakukan. Jadi, untuk dilanjutkan.