Hitungan Komunitas “Apa?” Dimana? Kapan? ”(ChGK) atau berapa banyak jabat tangan di depan seorang Teman?

Halo, Habr!

Liburan Tahun Baru adalah waktu yang tepat untuk istirahat dari IT Gunakan keahlian profesional dalam hobi favorit Anda. Sambil mencari-cari di situs peringkat ChGK olahraga , saya menemukan API yang luar biasa yang memungkinkan Anda untuk mendapatkan data pada semua game dari semua turnamen. Jadi saya mendapat ide untuk membuat grafik komunitas pakar dan menguji teori enam jabat tangan di komunitas yang secara geografis tersebar dan benar-benar offline. Di bawah gambar katom grafik dan statistik tidak berguna.

Untuk mulai dengan, program pendidikan singkat, apa itu olahraga ChGK.

Pengambilan data

Kami berasumsi bahwa para pemain akrab satu sama lain jika mereka bermain setidaknya satu kali di satu meja permainan. Berkat API yang bagus, mengunduh data tentang semua turnamen dan semua tim tidak menjadi masalah.

Di bawah spoiler, bahkan Sup Indah tidak digunakan, hanya permintaan. Notebook jupyter dengan semua kode sumber akan berada di akhir artikel.

url = 'https://rating.chgk.info/api/tournaments.json/?page={}' df = pd.DataFrame(columns=['name', 'start']) for i in range(1, 7): data = requests.get(url.format(i)).json() for item in data["items"]: df.loc[item["idtournament"]] = (item["name"], item["date_start"]) df.to_csv('tournaments.csv') 

Tetap mengunduh daftar nama permainan dari semua turnamen dan mengingat semua kenalan. Awalnya, saya berencana untuk menyimpan fakta-fakta permainan bersama dalam DataFrame, tetapi kecepatan menambahkan catatan baru menyedihkan. Oleh karena itu, kami akan menetapkan dari tupel (id1, id2), di mana id1, id2 adalah pengidentifikasi pemain yang akrab satu sama lain. Pada saat yang sama, singkirkan duplikat.

 df = pd.read_csv('tournaments.csv').set_index('Unnamed: 0') url = 'https://rating.chgk.info/api/tournaments/{}/recaps.json' links = set() for id in df.index: teams = requests.get(url.format(id)).json() for team in teams: t = team["recaps"] for i in range(len(t)): for j in range(i + 1, len(t)): first = int(t[i]["idplayer"]) second = int(t[j]["idplayer"]) if first < second: links.add((first, second)) else: links.add((second, first)) #    sleep(1) clear_output(wait=True) display('Current tournament: ' + str(df.index.get_loc(id) + 1) + '/' + str(len(df))) display('Links total: ' + str(len(links))) 

Mendapatkan grafik dan menjelajahi komponen yang terhubung

Jadi, persiapan data sudah selesai, saatnya untuk membuat grafik! Untuk melakukan ini, kita akan menggunakan networkx library, kapabilitas yang cukup untuk cluster kita.

 players = itertools.chain(*links) G = nx.Graph() G.add_nodes_from(players) for t in links: G.add_edge(*t) print(nx.info(G)) 

Sekarang ada sekitar dua ratus ribu orang di komunitas ChGK, dan rata-rata, seorang ahli karier telah bermain dengan 12 orang:

 Number of nodes: 198145 Number of edges: 1206076 Average degree: 12.1737 

Saatnya mencari tahu berapa banyak komponen yang terhubung dalam grafik penanggalan. Networkx memiliki fungsi hebat yang disebut connected_components yang melakukan apa yang Anda butuhkan:

 clusters_l = [len(c) for c in sorted(nx.connected_components(G), key=len, reverse=True)] print(clusters_l[:20]) 

Hampir tiga perempat pemain berada dalam satu komponen yang terhubung, sisanya dibagi menjadi subgraph yang sangat kecil. Ada lebih dari delapan ribu di antaranya.

 [145922, 153, 124, 74, 72, 56, 50, 47, 42, 40, 39, 39, 38, 38, 37, 36, 36, 36, 36, 35] 

Bahkan pada skala logaritmik, dominasi komponen utama terlihat mengesankan. Pada sumbu X - jumlah komponen dari yang terbesar hingga yang terkecil, pada sumbu Y - ukurannya (sumbu adalah logaritmik).

Apa yang menyebabkan distribusi orang yang sedemikian tidak merata dalam komponen yang terhubung? Menurut saya, intinya adalah ini:

• sekelompok kecil orang datang ke permainan untuk pertama kalinya dan dengan demikian membentuk kelompok kecil untuk 4-6 orang;
• jika kota ini sudah memiliki komunitas besar, cluster seperti itu akan dengan cepat bergabung dengan yang utama - hanya satu orang yang perlu bermain untuk tim dari cluster utama;
• jika di kota ChGK baru saja muncul, cluster akan hidup lebih lama, karena bermain untuk tim dari cluster utama lebih sulit.

Prosesnya menyerupai pembentukan tetesan hujan di awan: setetes besar menarik yang kecil dan tumbuh dengan cepat.

Sebelum berurusan dengan komponen utama, mari kita lihat komponen di tempat pertama atau kesembilan (saya menganggap komponen utama menjadi nol). Kami menguji hipotesis bahwa orang-orang di komponen ini berasal dari kota yang sama. Penikmat tidak memiliki keterikatan pada kota (yang logis di dunia modern kita). Namun, Anda dapat melihat port rumah tim yang ia mainkan terakhir kali

 for i in range(1, 10): _g = list(sorted(nx.connected_components(G), key=len, reverse=True)[i]) s = pd.Series() p_url = 'https://rating.chgk.info/api/players/{}/tournaments.json' t_url = 'https://rating.chgk.info/api/teams/{}.json' for player in _g: data = requests.get(p_url.format(player)).json() for item in data: team_id = data[item]["tournaments"][0]["idteam"] data = requests.get(t_url.format(team_id)).json() town = data[0]["town"] s.at[len(s)] = town print(' #{}'.format(i)) print(s.value_counts()) 

Piring ringkasan:

Ya, kelompok kecil hampir seluruhnya berasal dari satu kota. Harap perhatikan komponen tujuh puluh dua warga Tambov, yang terkait dengan Luksemburg. Di tempat ketujuh dan kesembilan adalah komponen dari Gorno-Altaysk, yang karena beberapa alasan tidak saling berhubungan. Saya siap membayangkan perjuangan dua klan ChGK-ash, seperti Montecca dan Capulet, yang berjuang untuk menguasai kota.
Saya kira bahwa dalam waktu dekat komponen-komponen ini akan bergabung menjadi yang utama tetapi akan terus berjuang .

Komponen utama konektivitas

Jadi, kita sampai pada komponen utama. Kami akan mendapatkan subgraf yang diinginkan dan melihat statistiknya:

 subgraph_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[0]) subgraph = G.subgraph(subgraph_v) print(nx.info(subgraph)) 

Jumlah rata-rata koneksi ternyata lebih banyak.

 Number of nodes: 145922 Number of edges: 1070504 Average degree: 14.6723 

Dan berapa jumlah maksimum koneksi per pemain?

 for t in sorted(G.degree, key=lambda x: x[1], reverse=True)[:10]: print(' {}   {} '.format(t[0], t[1])) 

  42511   818   15051   798   29800   678   23020   666   16581   662   5328   657   29887   651   15811   645   30352   605   1055   602  

Terus terang, saya sedikit terkejut dengan jumlahnya. Jika Anda bermain dengan tim baru setiap kali, maka Anda akan membutuhkan 818/5 ≈ 164 game untuk mencapai tempat pertama. Luar biasa.
Kami akan mengingat dua ahli pertama dalam peringkat ini dan akan menggunakan keterampilan komunikasi mereka lebih lanjut.
Mari kita perkirakan berapa banyak kenalan terdekat yang dimiliki oleh seorang pakar rata-rata:

 _count = 50 values = nx.degree_histogram(subgraph) plt.figure(figsize=(16, 8), dpi=80) plt.plot(range(_count),values[:_count],'ro-') # in-degree plt.xlabel(' ', fontsize=18) plt.xticks(range(0,_count, 5)) plt.ylabel(' ', fontsize=18) plt.title(' ', fontsize=22) plt.show() 

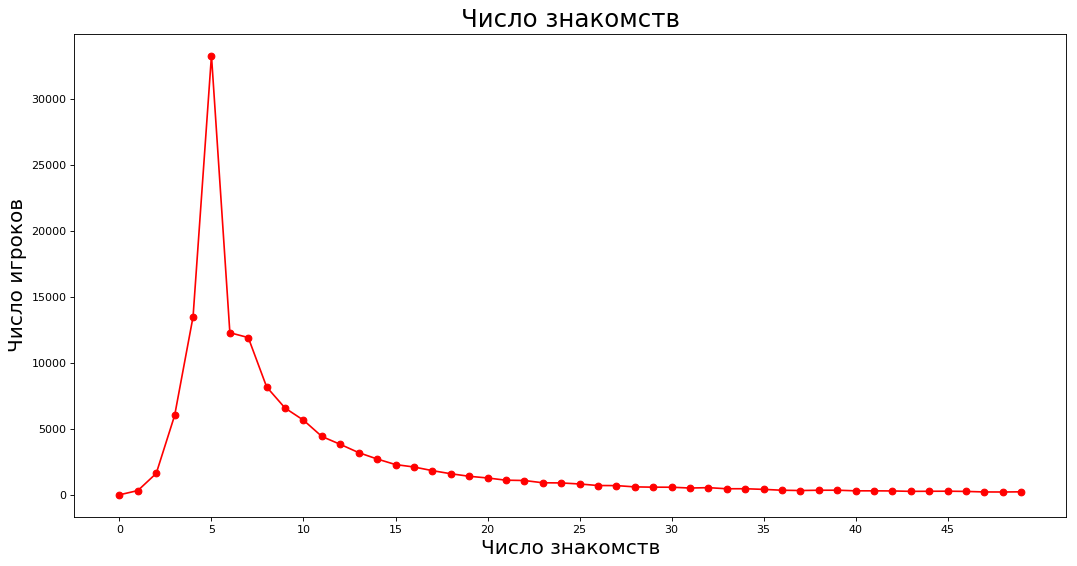
Pada sumbu X - jumlah kenalan terdekat, pada sumbu Y - jumlah pakar yang memiliki jumlah kenalan yang sesuai. Misalnya, sekitar 40.000 pakar masing-masing memiliki lima kenalan.
Perhatikan bahwa fashion memiliki 5 kenalan (lucu bahwa hingga enam orang dapat hadir di meja). Pada saat yang sama, rata-rata aritmatika dari jumlah kenalan adalah 14,67, dan median adalah 7. Faktanya adalah bahwa pria dari peringkat di atas sangat melebih-lebihkan rata-rata. Jika seratus orang tidak bermain di ChGK, dan satu memiliki 800 kenalan, maka rata-rata mereka bermain di ChGK.

Jarak ke Pemain

Karena menghitung diameter grafik semacam itu agak sulit , mari lakukan lebih mudah: ambil daftar beberapa pemain dan temukan jarak maksimum terdekat dari mereka ke pakar lain. Sebagai pemain ini, saya mengambil beberapa ahli terkenal, saya sendiri, pemain acak dan dua ahli dengan jumlah kenalan terbesar (lihat peringkat di atas). Inilah yang terjadi:

 famous_players = {9808: ' ', 5195: ' ', 25882: ' ', 29333: ' ', 118622: ' ', 42511: ' ', 15051: ' ', 118621: ' '} for key in famous_players: print('{}: {} -      ' .format(famous_players[key], nx.eccentricity(subgraph, v=key))) 

  : 12 -        : 12 -        : 12 -        : 12 -        : 13 -        : 12 -        : 13 -        : 13 -       

Ternyata rumusan kuat dari teori enam jabat tangan (dua orang yang dipisahkan oleh tidak lebih dari lima tingkat teman bersama) tidak benar. Diameter grafik kemungkinan besar adalah 13-14.
Bagaimana dengan kata-kata yang lebih lemah ( rata-rata dua orang dipisahkan oleh tidak lebih dari lima tingkat teman yang sama)?

 for key in famous_players: paths = nx.shortest_path_length(subgraph, source=key).values() print('{}: {} -      ' .format(famous_players[key], sum(paths) / len(paths))) 

  : 3.941461876893135 -        : 3.7971107852140182 -        : 3.89353216101753 -        : 3.8634887131481204 -        : 4.1443373857266215 -        : 3.575478680390894 -        : 3.608674497334192 -        : 4.564102739819904 -       

Jika kita melonggarkan kata-kata, maka teorinya terpenuhi - rata-rata di antara para ahli pada tingkat 4-5 kenalan. Kami memplot berapa banyak orang yang akrab dengan penikmat acak A. Druzem secara langsung, melalui satu, dua, dll. penikmat.

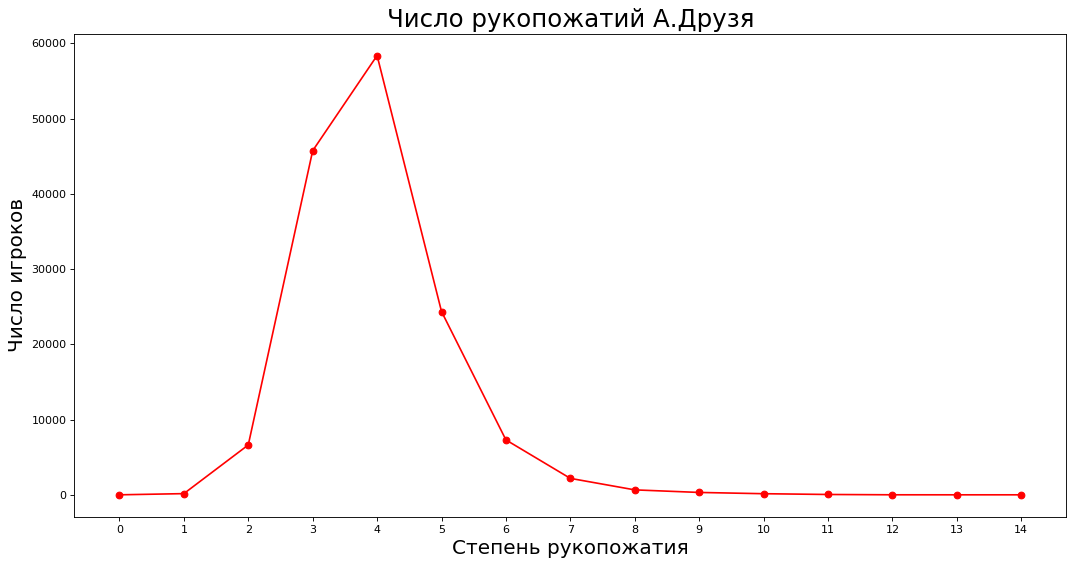
 paths = nx.shortest_path_length(subgraph, source=9808) neighbours = [0] * 15 for k in paths: neighbours[paths[k]] += 1 _count = 15 plt.figure(figsize=(16, 8), dpi=80) plt.plot(range(_count),neighbours[:_count],'ro-') # in-degree plt.xlabel(' ', fontsize=18) plt.xticks(range(_count)) plt.ylabel(' ', fontsize=18) plt.title('  .', fontsize=22) plt.show() 

Pada sumbu X, tingkat kenalan dengan A. Druzem (langsung, melalui satu, dua, dll.), Pada sumbu Y, jumlah ahli yang akrab dengan A. Druzem dengan cara ini.

Grafik sosial

Karena membangun grafik untuk hampir 200 ribu orang bukanlah ide yang baik, kami akan membuatnya lebih mudah: kami akan membangun komponen konektivitas Kerch dan grafik orang yang terkait dengan penulis.

Komponen kerch

 little_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[1]) little = G.subgraph(little_v) plt.figure(figsize=(24, 12), dpi=200) pos = nx.kamada_kawai_layout(little) nx.draw(little, pos=pos, node_size=100, edge_color='gray', node_color=[val for (node, val) in little.degree()], cmap=plt.cm.jet) plt.show() 

Anda dapat melihat pemisahan komponen menjadi beberapa tim. Selain itu, tim-tim tersebut saling berhubungan dengan bantuan, sebagai aturan, dari satu atau dua penikmat yang ramah. Di tengah adalah inti yang agak kecil dari para ahli yang bermain dengan sejumlah besar pemain lain.

Hitungan satu orang

Kami akan menemukan kenalan terdekat dari satu orang dan melihat bagaimana mereka terkait. Untuk menyederhanakan grafik, kami tidak akan menambahkan orang itu sendiri (dia sudah terhubung dengan semua orang)

 id = 118622 ego_graph = [n for n in G.neighbors(id)] #ego_graph.append(id) ego_graph = G.subgraph(ego_graph) plt.figure(figsize=(24, 16), dpi=200) pos = nx.kamada_kawai_layout(ego_graph) nx.draw(ego_graph, pos=pos, node_size=100, edge_color='gray', node_color=[val for (node, val) in ego_graph.degree()], cmap=plt.cm.jet) plt.show() 

Grafiknya jauh lebih padat, inti 10-15 orang yang akrab satu sama lain dapat dibedakan. Ukuran klik maksimum adalah 13.

Kesimpulan

• Jauh lebih sulit untuk mengenal seseorang di ChGK olahraga daripada di jejaring sosial, Anda harus offline dan bermain setidaknya satu turnamen. Pada saat yang sama, para ahli tersebar di seluruh dunia. Namun, jarak rata - rata antar pakar memang kurang dari lima.
• Situs pemeringkatan menggunakan nomor Snyatkovsky , yang merupakan analog dari nomor Erdös di dunia ChGK. Tn. Snyatkovsky sendiri menempati posisi ketiga dalam peringkat kami para penikmat paling ramah.
• Kode dari sebuah artikel di github saya.
• Untuk komentar yang berharga, penulis berterima kasih kepada White Noise dan Who Framed Roger Federer, Mikhail Akulov, Vera Terentyeva, dan Firemoon .