Halo semuanya! Liburan Tahun Baru telah berakhir, yang berarti bahwa kami siap kembali untuk membagikan materi yang bermanfaat dengan Anda. Terjemahan artikel ini disiapkan untuk mengantisipasi peluncuran aliran baru pada kursus "Algoritma untuk Pengembang" .
Ayo pergi!
Metode back propagation of error mungkin merupakan komponen paling mendasar dari jaringan saraf. Ini pertama kali dideskripsikan pada 1960-an dan hampir 30 tahun kemudian dipopulerkan oleh Rumelhart, Hinton dan Williams dalam sebuah artikel berjudul
"Mempelajari representasi dengan kesalahan perbanyakan kembali" .
Metode ini digunakan untuk secara efektif melatih jaringan saraf menggunakan aturan rantai yang disebut (aturan diferensiasi fungsi kompleks). Sederhananya, setelah setiap melewati jaringan, propagasi kembali melakukan oper pada arah yang berlawanan dan menyesuaikan parameter model (bobot dan perpindahan).
Pada artikel ini, saya ingin mempertimbangkan secara rinci dari sudut pandang matematika proses pembelajaran dan mengoptimalkan jaringan saraf 4-layer yang sederhana. Saya percaya ini akan membantu pembaca memahami cara kerja backpropagation, serta menyadari signifikansinya.
Mendefinisikan model jaringan saraf
Jaringan saraf empat-lapisan terdiri dari empat neuron di lapisan input, empat neuron di lapisan tersembunyi dan 1 neuron di lapisan output.
Gambar sederhana dari jaringan saraf empat lapis.Lapisan input
Dalam gambar, neuron ungu mewakili input. Mereka dapat jumlah skalar sederhana atau lebih kompleks - vektor atau matriks multidimensi.
Persamaan yang menjelaskan input xi.Set aktivasi pertama (a) sama dengan nilai input. "Aktivasi" adalah nilai neuron setelah menerapkan fungsi aktivasi. Lihat di bawah untuk detail lebih lanjut.
Lapisan tersembunyi
Nilai akhir dalam neuron tersembunyi (dalam gambar hijau) dihitung menggunakan input berbobot z
l pada lapisan I dan aktivasi
I pada lapisan L. Untuk lapisan 2 dan 3, persamaannya adalah sebagai berikut:
Untuk l = 2:
Untuk l = 3:
W
2 dan W
3 adalah bobot pada layer 2 dan 3, dan b
2 dan b
3 adalah offset pada lapisan ini.
Aktivasi
2 dan
3 dihitung menggunakan fungsi aktivasi f. Sebagai contoh, fungsi ini f adalah non-linear (seperti
sigmoid ,
ReLU dan
hiperbolik tangen ) dan memungkinkan jaringan untuk mempelajari pola kompleks dalam data. Kami tidak akan membahas tentang bagaimana fungsi aktivasi bekerja, tetapi jika Anda tertarik, saya sangat merekomendasikan membaca
artikel yang luar biasa
ini .
Jika Anda melihat lebih dekat, Anda akan melihat bahwa semua x, z
2 , a
2 , z
3 , a
3 , W
1 , W
2 , b
1 dan b
2 tidak memiliki indeks yang lebih rendah seperti pada gambar jaringan saraf empat lapis. Faktanya adalah bahwa kami menggabungkan semua nilai parameter ke dalam matriks yang dikelompokkan berdasarkan layer. Ini adalah cara standar untuk bekerja dengan jaringan saraf, dan cukup nyaman. Namun, saya akan pergi melalui persamaan sehingga tidak ada kebingungan.
Mari kita ambil layer 2 dan parameternya sebagai contoh. Operasi yang sama dapat diterapkan ke semua lapisan jaringan saraf.
W
1 adalah matriks bobot dimensi
(n, m) , di mana
n adalah jumlah neuron keluaran (neuron pada lapisan berikutnya), dan
m adalah jumlah neuron input (neuron pada lapisan sebelumnya). Dalam kasus kami,
n = 2 dan
m = 4 .
Di sini, angka pertama dalam subskrip dari setiap bobot sesuai dengan indeks neuron pada lapisan berikutnya (dalam kasus kami, ini adalah lapisan tersembunyi kedua), dan angka kedua sesuai dengan indeks neuron pada lapisan sebelumnya (dalam kasus kami, ini adalah lapisan input).
x adalah vektor input dimensi (
m , 1), di mana
m adalah jumlah neuron input. Dalam kasus kami,
m = 4.
b
1 adalah vektor perpindahan dimensi (
n , 1), di mana
n adalah jumlah neuron dalam lapisan saat ini. Dalam kasus kami,
n = 2.
Dengan mengikuti persamaan untuk z2
, kita dapat menggunakan definisi W1, x dan b1 di
atas untuk mendapatkan persamaan z2:
Sekarang perhatikan dengan seksama ilustrasi jaringan saraf di atas:
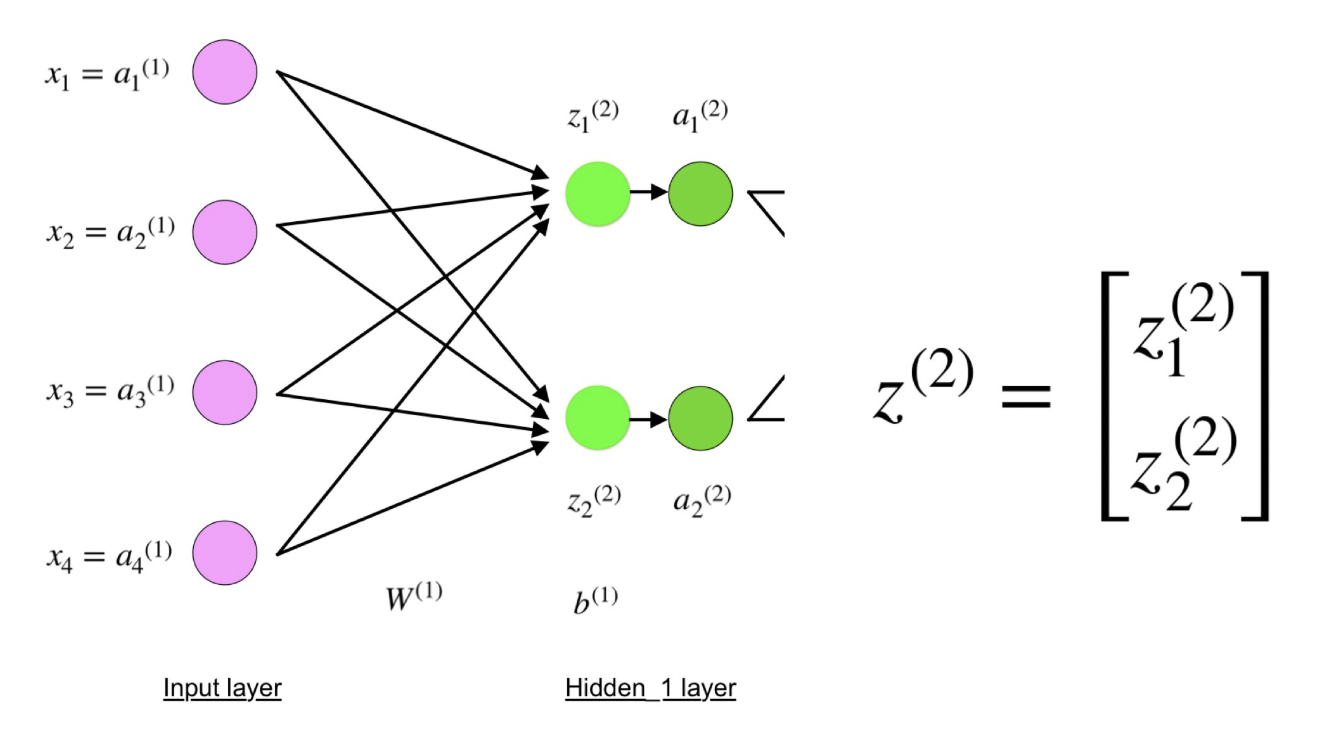
Seperti yang Anda lihat, z
2 dapat diekspresikan dalam bentuk z
1 2 dan z
2 2 , di mana z
1 2 dan z
2 2 adalah jumlah dari produk dari masing-masing nilai input x
i dengan bobot yang sesuai W
ij 1 .
Ini mengarah ke persamaan yang sama untuk z
2 dan membuktikan bahwa representasi matriks z
2 , a
2 , z
3 dan a
3 adalah benar.
Lapisan output
Bagian terakhir dari jaringan saraf adalah lapisan keluaran, yang memberikan nilai prediksi. Dalam contoh sederhana kami, itu disajikan dalam bentuk neuron tunggal bernoda biru dan dihitung sebagai berikut:
Sekali lagi, kami menggunakan representasi matriks untuk menyederhanakan persamaan. Anda dapat menggunakan metode di atas untuk memahami logika yang mendasarinya.
Distribusi dan evaluasi langsung
Persamaan di atas membentuk distribusi langsung melalui jaringan saraf. Berikut ini gambaran singkatnya:
(1) - lapisan input
(2) - nilai neuron di lapisan tersembunyi pertama
(3) - nilai aktivasi pada lapisan tersembunyi pertama
(4) - nilai neuron di lapisan kedua yang tersembunyi
(5) - nilai aktivasi di tingkat tersembunyi kedua
(6) - lapisan keluaranLangkah terakhir dalam operan langsung adalah mengevaluasi nilai output yang diprediksi relatif terhadap nilai output yang diharapkan
y .
Output y adalah bagian dari set data pelatihan (x, y), di mana
x adalah input (seperti yang kita ingat dari bagian sebelumnya).
Estimasi antara
s dan
y terjadi melalui fungsi kerugian. Ini bisa sederhana sebagai
kesalahan standar atau lebih kompleks sebagai
cross entropy .
Kami menyebut fungsi kerugian ini C dan menyatakannya sebagai berikut:
Di mana
biaya dapat sama dengan kesalahan standar, entropi silang, atau fungsi kerugian lainnya.
Berdasarkan nilai C, model “tahu” berapa parameternya perlu disesuaikan untuk mendekati nilai output
y yang diharapkan . Ini terjadi menggunakan metode backpropagation.
Kembali propagasi kesalahan dan perhitungan gradien
Berdasarkan artikel 1989, metode backpropagation:
Secara konstan menyesuaikan bobot koneksi dalam jaringan untuk meminimalkan ukuran perbedaan antara vektor keluaran aktual jaringan dan vektor keluaran yang diinginkan .
dan
... memungkinkan untuk membuat fungsi-fungsi baru yang berguna yang membedakan backpropagation dari metode sebelumnya dan lebih sederhana ...Dengan kata lain, propagasi balik ditujukan untuk meminimalkan fungsi kerugian dengan menyesuaikan bobot dan offset jaringan. Tingkat penyesuaian ditentukan oleh gradien dari fungsi kerugian sehubungan dengan parameter ini.
Satu pertanyaan muncul:
Mengapa menghitung gradien ?
Untuk menjawab pertanyaan ini, pertama-tama kita perlu merevisi beberapa konsep komputasi:
Gradien fungsi C (x
1 , x
2 , ..., x
m ) pada x adalah
vektor turunan parsial C
sehubungan dengan
x .
Turunan dari fungsi C mencerminkan sensitivitas terhadap perubahan nilai fungsi (nilai output) relatif terhadap perubahan dalam argumen
x (
nilai input ). Dengan kata lain, turunan memberi tahu kita ke arah mana C. bergerak.
Gradien menunjukkan betapa perlu untuk mengubah parameter
x (dalam arah positif atau negatif) untuk meminimalkan C.
Gradien ini dihitung menggunakan metode yang disebut
aturan rantai.
Untuk satu berat (w
jk )
l, gradiennya adalah:
(1) Aturan rantai
(2) Menurut definisi, m adalah jumlah neuron per l - 1 lapisan
(3) Perhitungan derivatif
(4) Nilai akhir
Serangkaian persamaan yang serupa dapat diterapkan ke (b j ) l :
(1) Aturan rantai
(2) Perhitungan derivatif
(3) Nilai akhirBagian umum dalam kedua persamaan sering disebut "gradien lokal" dan dinyatakan sebagai berikut:
"Gradien lokal" dapat dengan mudah ditentukan menggunakan aturan rantai. Saya tidak akan melukis proses ini sekarang.
Gradien memungkinkan pengoptimalan parameter model:
Sampai kriteria berhenti tercapai, berikut ini dilakukan:
Algoritma untuk mengoptimalkan bobot dan offset (juga disebut gradient descent)
- Nilai awal w dan b dipilih secara acak.
- Epsilon (e) adalah kecepatan belajar. Ini menentukan efek gradien.
- w dan b adalah representasi matriks dari bobot dan offset.
- Turunan C sehubungan dengan w atau b dapat dihitung dengan menggunakan turunan sebagian C sehubungan dengan bobot atau offset individu.
- Kondisi terminasi dipenuhi segera setelah fungsi kerugian diminimalkan.
Saya ingin mengabdikan bagian terakhir dari bagian ini untuk contoh sederhana di mana kita menghitung gradien C sehubungan dengan satu berat (w
22 )
2 .
Mari memperbesar bagian bawah jaringan saraf yang disebutkan di atas:
Representasi visual backpropagation dalam jaringan sarafBerat (w
22 )
2 menghubungkan (a
2 )
2 dan (z
2 )
2 , jadi menghitung gradien membutuhkan penerapan aturan rantai pada (z
2 )
3 dan (a
2 )
3 :
Perhitungan nilai akhir dari turunan C dari (a
2 )
3 membutuhkan pengetahuan tentang fungsi C. Karena C tergantung pada (a
2 )
3 , perhitungan derivatif harus sederhana.
Saya harap contoh ini telah berhasil menjelaskan matematika di balik menghitung gradien. Jika Anda ingin tahu lebih banyak, saya sangat menyarankan agar Anda memeriksa serangkaian artikel NLP Stanford, di mana Richard Socher memberikan 4 penjelasan bagus untuk propaganda balik.
Komentar penutup
Dalam artikel ini, saya menjelaskan secara rinci bagaimana perbanyakan kembali kesalahan bekerja di bawah tenda menggunakan metode matematika seperti menghitung gradien, aturan rantai, dll. Mengetahui mekanisme algoritme ini akan memperkuat pengetahuan Anda tentang jaringan saraf dan memungkinkan Anda merasa nyaman saat bekerja dengan model yang lebih kompleks. Semoga sukses dalam perjalanan belajar Anda yang dalam!
Itu saja. Kami mengundang semua orang ke webinar gratis dengan tema "Pohon segmen: sederhana dan cepat . "