🏆 🤵🏾 🙆🏻 Visualisasi batas-batas solusi classifier berbasis gambar 🎓 🅱️ 🗻

Pendahuluan

Memahami bagaimana classifier memecah ruang multidimensi awal atribut menjadi banyak kelas target adalah langkah penting untuk menganalisis masalah klasifikasi dan mengevaluasi solusi yang diperoleh dengan menggunakan pembelajaran mesin.

Pendekatan modern untuk memvisualisasikan keputusan pengklasifikasi terutama menggunakan sebar plot yang hanya dapat menampilkan proyeksi sampel pelatihan asli, tetapi tidak secara eksplisit menunjukkan batas-batas pengambilan keputusan yang sebenarnya, atau menggunakan struktur internal pengklasifikasi (misalnya, kNN, SVM, Regresi Logistik) yang mudah untuk membangun geometri interpretasi. Metode ini tidak cocok untuk visualisasi, misalnya, dari pengklasifikasi jaringan saraf.

Artikel "Visualisasi Berbasis Batas Batas Keputusan" (Rodrigues et al., 2018) mengusulkan metode alternatif yang efektif, indah dan cukup sederhana untuk memvisualisasikan solusi pengklasifikasi, yang tanpa kekurangan di atas. Yaitu, metode ini cocok untuk pengklasifikasi dalam bentuk apa pun dan membangun batas pengambilan keputusan menggunakan gambar dengan laju pengambilan sampel yang sewenang-wenang.

Posting ini adalah ikhtisar singkat tentang ide-ide utama dan hasil dari artikel asli.

Deskripsi Metode

Dasar dari metode ini adalah pengambilan sampel terbalik (eng. Upsampling) dari bidang gambar $\ mathbb {R} ^ 2$ yang diwakili oleh satu set piksel ke dalam ruang fitur $\ mathbb {R} ^ n$ .

Metode ini membutuhkan dua pemetaan $P: \ mathbb {R} ^ n \ to \ mathbb {R} ^ 2$ - Proyeksi langsung dari ruang fitur ke bidang gambar dan kebalikannya $P ^ {- 1}: \ mathbb {R} ^ 2 \ to \ mathbb {R} ^ n$ . Seperti pemetaan tersebut, LAMP (Joia et al. 2011) dan iLAMP (Amorim et al. 2012) , masing-masing, digunakan.

Membangun

Untuk membangun gambar, Anda perlu menetapkan warna untuk setiap piksel. Untuk ini, untuk setiap piksel akan menemukan $N \ geq 1$ poin dari sumber hyperspace mana - parameter yang ditentukan oleh pengguna. Biarkan pikselnya sudah $n (y) \ geq 0$ prototipe nyata dari set pelatihan. Maka pilihlah secara merata $\ maks (N - n (y), 0)$ titik yang tersisa dari permukaan piksel dan temukan prototipe untuk mereka melalui proyeksi belakang $x_i = P ^ {- 1} (y_i)$ . Jadi, warna masing-masing piksel akan ditentukan setidaknya titik ruang sumber, dan seluruh gambar akan dilukis.

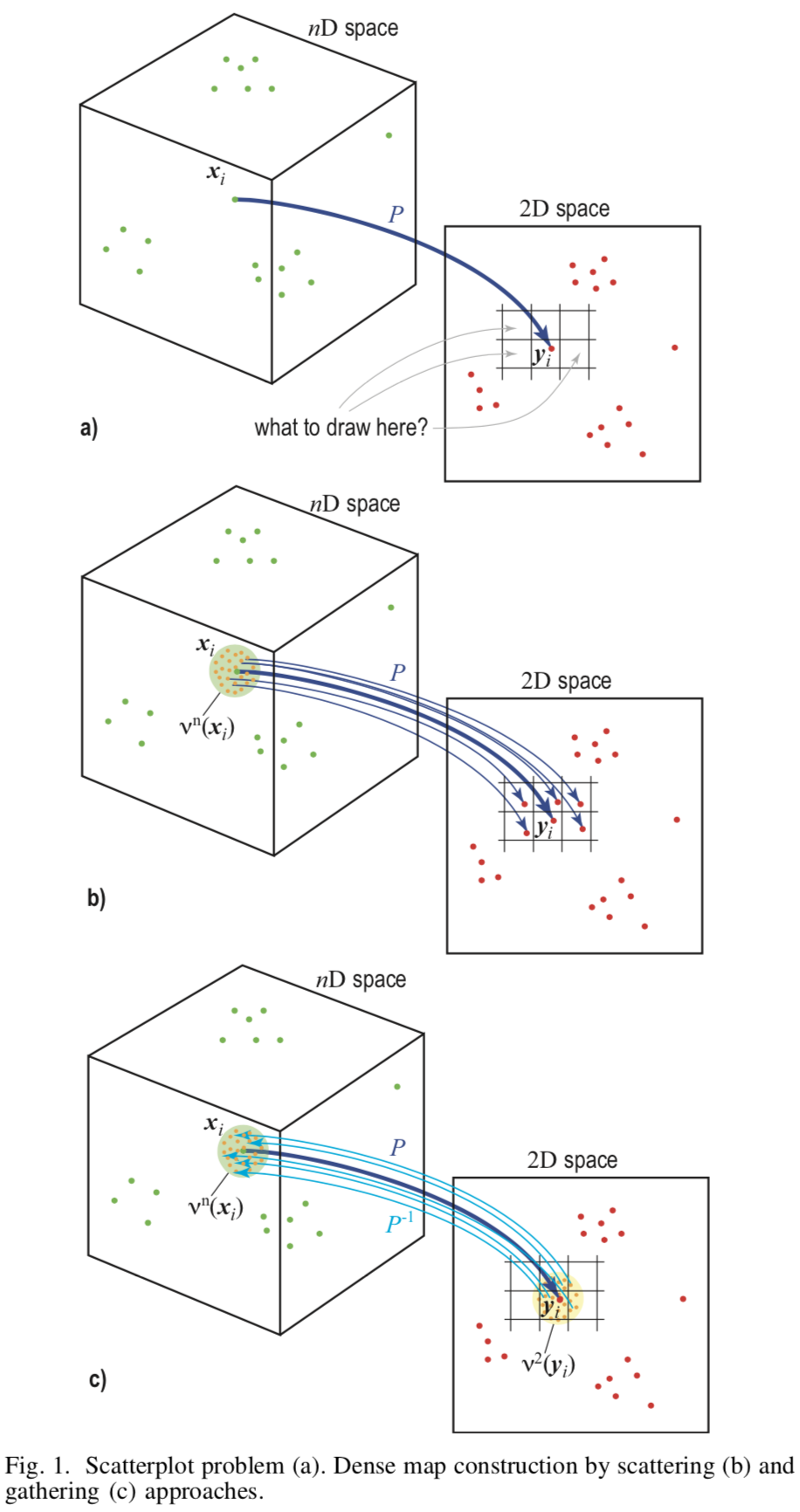
Metode perbedaan
[Gbr.1] Ilustrasi skematis dari berbagai pendekatan

Definisi warna

Warna setiap piksel ditentukan oleh suara mayoritas untuk label kelas dari preimage yang sesuai.

$d (y) = \ text {argmax} _ {k \ dalam C} \ sum_ {y_i \ in y} [f (P ^ {- 1} (y_i)) = k]$

dimana - Banyak dari semua kelas, $f: \ mathbb {R} ^ n \ ke C$ - penggolong.

Setiap kelas akan diberi nada (eng. Hue) H_T (k) - jika proyeksi memiliki poin dari sampel nyata, dan nada sedikit berubah $H _ {\ text {synth}} (k)$ untuk piksel yang hanya memiliki titik-titik sintetis.

Kebingungan

Tentukan pencampuran piksel (dari kebingungan bahasa Inggris) c (y) - sebagai perbandingan jumlah label dari kelas yang ada dengan jumlah total gambar terbalik piksel :

$c (y) = \ frac {\ max_ {k \ dalam C} \ sum_ {y_i \ in y} [f (P ^ {- 1} (y_i)) = k]} {| y |}$

Nilai tinggi c (y) menunjukkan konsistensi classifier, sementara nilai yang rendah menandakan pendekatan untuk batas pemisah. Blend informasi yang dikodekan dalam saturasi piksel S (y) - semakin tinggi konsistensi, semakin tinggi saturasi.

Kepadatan

Meskipun minimum telah dihasilkan poin preimage untuk setiap piksel, mungkin ada piksel yang ada lebih banyak poin nyata dari set pelatihan. Pixel semacam itu harus dipertimbangkan saat rendering. Untuk melakukan ini, masukkan kerapatan piksel $\ rho (y)$ sebagai jumlah titik gambar terbalik dari $\ mathbb {R} ^ n$ . Orang dapat menggunakan kerapatan ini secara langsung untuk menentukan kecerahan piksel sebagai $V (y) = \ frac {\ rho (y)} {\ rho_ {max}}$ , tetapi penulis artikel menunjukkan bahwa ini tidak memberikan hasil yang diinginkan, karena beberapa nada jelas lebih gelap dari yang lain. Oleh karena itu, pengaturan yang lebih canggih digunakan pada saat yang sama saturasi dan kecerahan melalui parameter kepadatan yang dinormalisasi.

$\ hat {\ rho} = maks (\ frac {1} {20} \ frac {\ rho} {\ rho_ {avg}}, 1)$

Lalu jika $\ hat {\ rho} \ dalam [0, 0,5]$ - Kecerahan secara linear tergantung pada parameter di dalamnya $[V_ {min} = 0,1, V_ {max} = 1]$ . Di $\ hat {\ rho} \ dalam [0,5, 1]$ mulai tumbuh saturasi linear dari $S_ {min} = 0,2$ sebelumnya $S_ {maks} = 1$ .

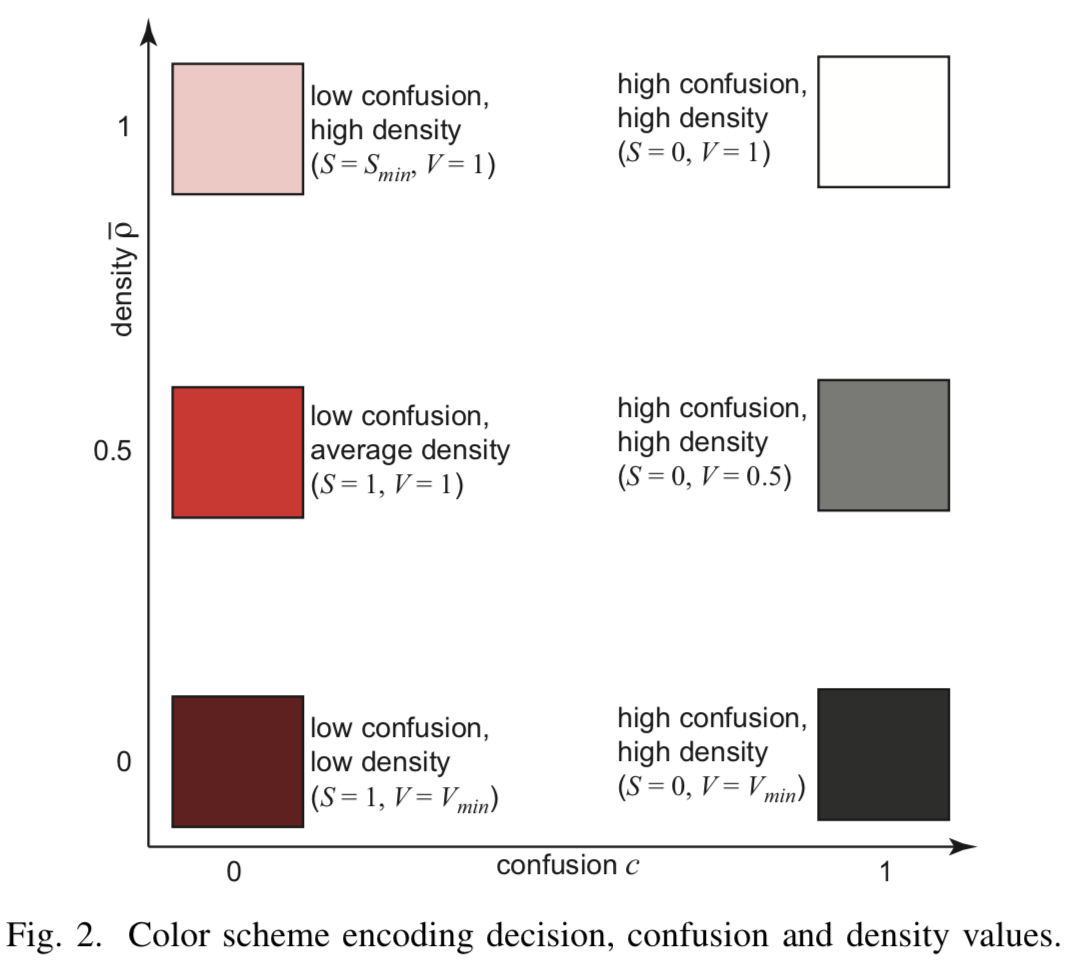
[Gbr.2] Pengodean warna

Eksperimen dan Hasil

Untuk percobaan, masalah klasifikasi biner pada set gambar digital MNIST dan klasifikasi multi-kelas pada Dataset Segmentasi Gambar , yang berisi 2.310 gambar dibagi menjadi 7 kelas, diselesaikan. Ada 19 atribut untuk setiap gambar.

Hasil pencitraan dengan berbagai pengaturan resolusi dan jumlah minimum prototipe untuk binary classifier LogisticRegression pada MNIST ditunjukkan pada gambar [3]. Kelas dipisahkan oleh garis lurus dengan akurasi tinggi dan algoritma visualisasi melakukan pekerjaan yang sangat baik. Dengan resolusi yang meningkat, awan titik sumber hampir sepenuhnya larut di antara banyak titik yang dihasilkan.

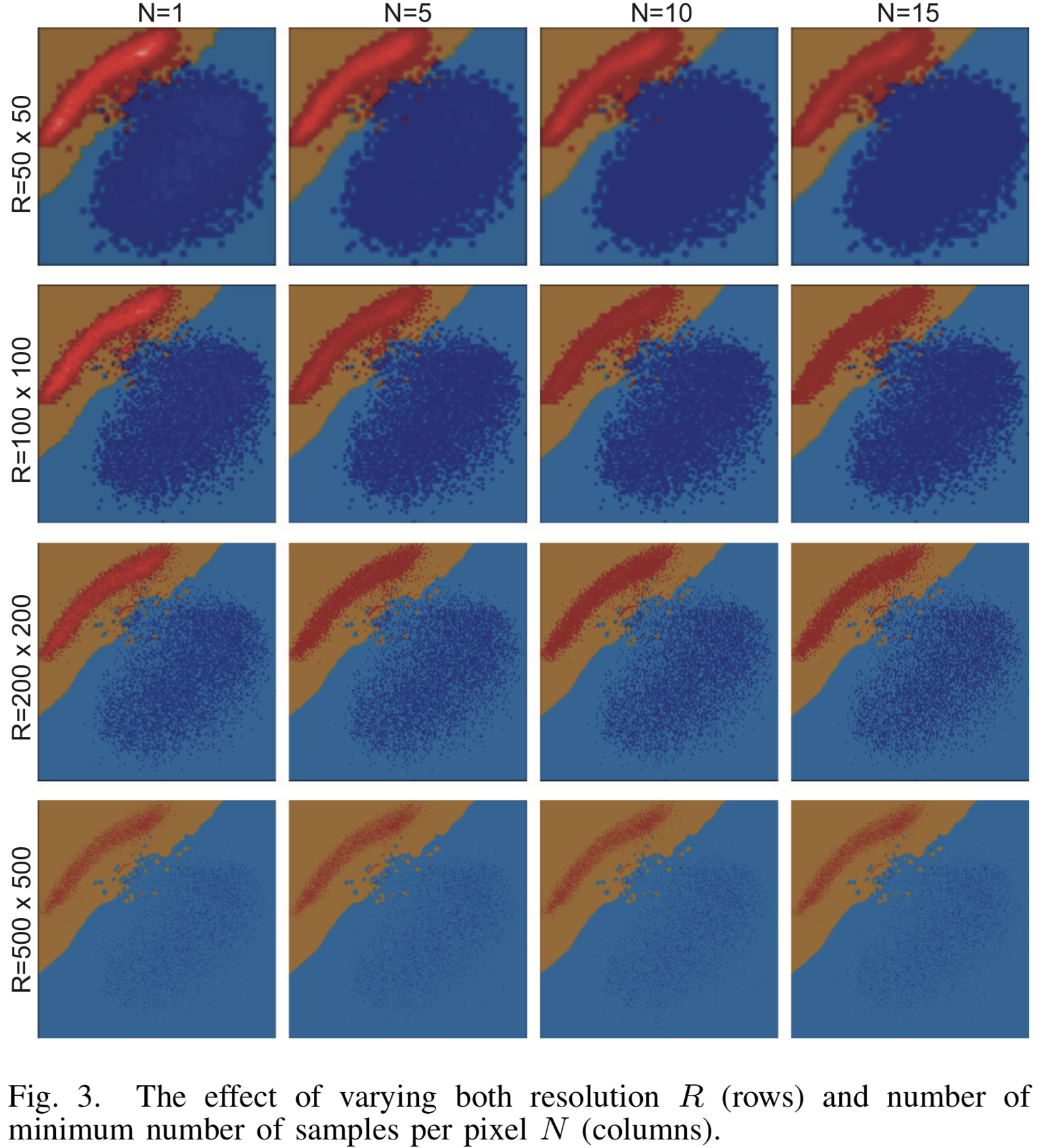
Pengodean warna
[Gambar. 3] Hasil visualisasi untuk berbagai parameter resolusi dan jumlah sampel minimum N untuk classifier LogisticRegression

Visualisasi kapan $R = 500 \ text {x} 500, N = 5$ untuk tiga pengklasifikasi yang berbeda untuk multi-klasifikasi pada gambar [4]. Proyeksi titik awal sangat beragam, dan tidak mungkin untuk membangun batas pemisah eksplisit di tempat-tempat di mana proyeksi dari kasus uji diakumulasikan. Namun, selain dari cluster utama, batas kelas eksplisit diperoleh, informasi tentang yang tidak ditampilkan pada proyeksi biasa, tetapi diperoleh hanya dengan bantuan titik sintetik.

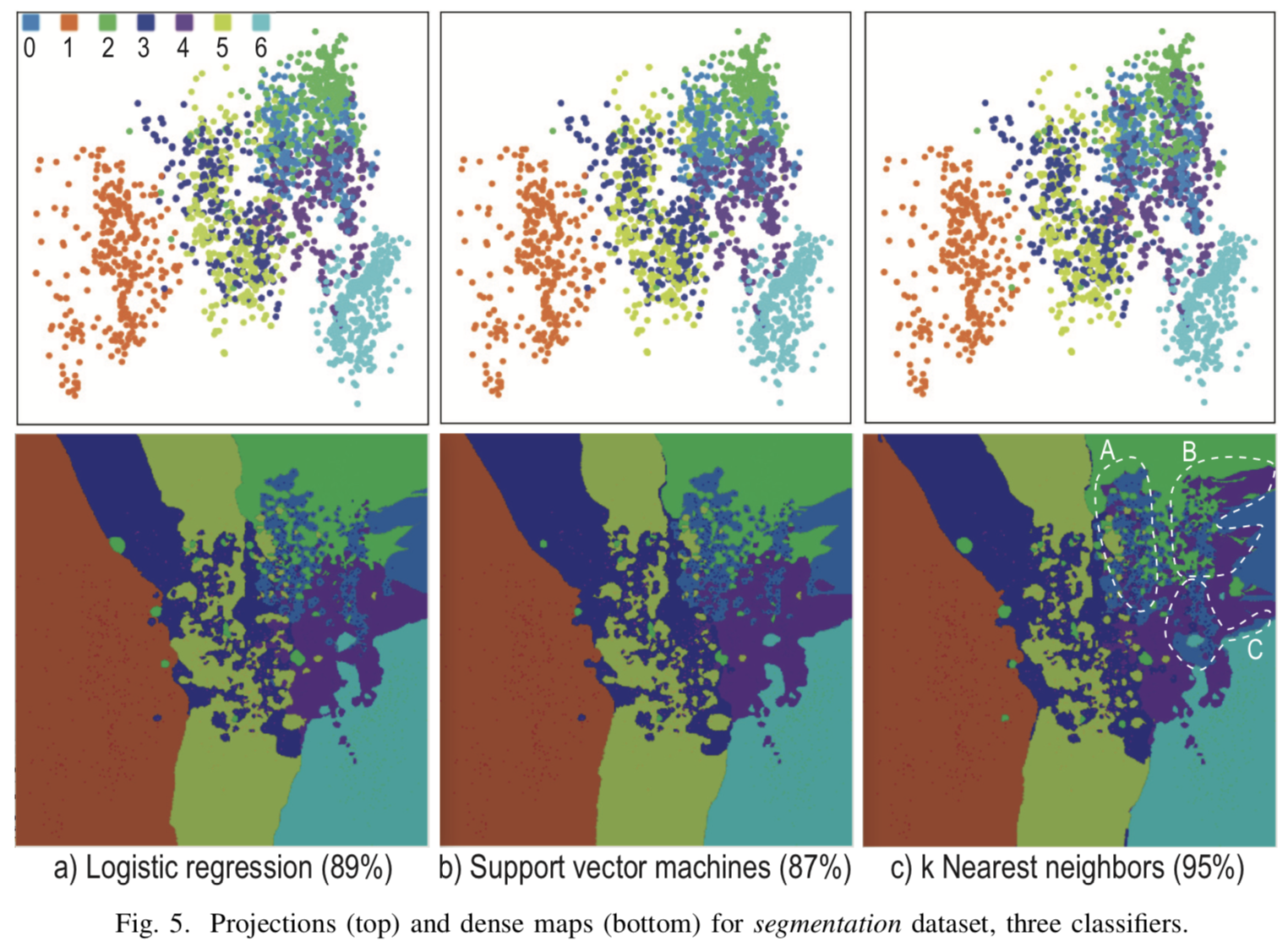
Pengodean warna
[Gambar. 4] Hasil dari visualisasi tiga pengklasifikasi yang berbeda untuk k = 7, R = 500x500, N = 5

Kesimpulan

Visualisasi batas kelas dapat digunakan dalam konstruksi dan debugging algoritma yang menentukan, dalam pemilihan hyperparameters, dalam perang melawan pelatihan ulang, untuk mempresentasikan dan menganalisis hasilnya.

Metode yang dideskripsikan oleh penulis artikel asli dapat digunakan untuk masalah klasifikasi di mana data direpresentasikan sebagai seperangkat tanda-tanda dimensi tetap. Tidak seperti algoritma visualisasi lainnya, pendekatan ini dapat digunakan untuk pengklasifikasi kompleks yang sewenang-wenang dan untuk kumpulan data dengan sejumlah contoh acak, bahkan dengan yang sangat kecil, karena bahkan dengan yang kecil Algoritma bekerja secara stabil, tanpa kehilangan banyak kualitas.

Visualisasi batas-batas solusi classifier berbasis gambar