bab sebelumnya

30. Interpretasi Kurva Belajar: Bias Besar

Misalkan kurva kesalahan Anda pada sampel validasi terlihat seperti ini:

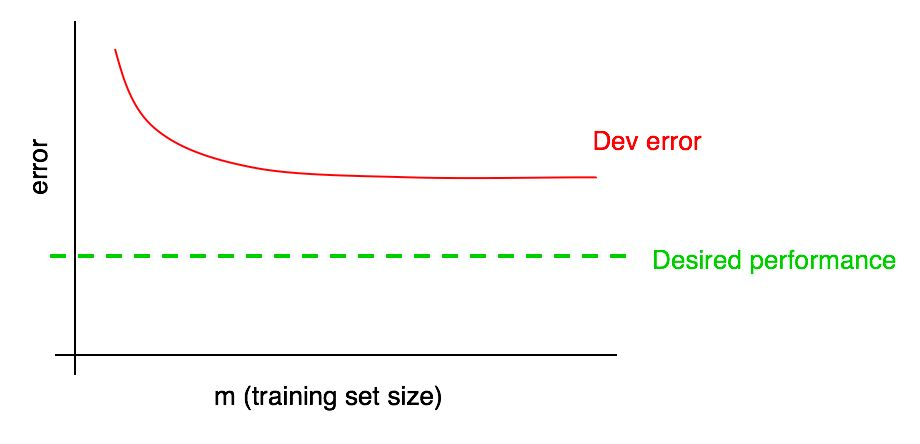
Kami telah mengatakan bahwa jika kesalahan algoritme dalam sampel validasi mencapai dataran tinggi, Anda tidak mungkin mencapai tingkat kualitas yang diinginkan hanya dengan menambahkan data.

Tetapi sulit untuk membayangkan bagaimana ekstrapolasi kurva ketergantungan kualitas algoritma pada sampel validasi (Dev error) ketika menambahkan data akan terlihat seperti. Dan jika sampel validasi kecil, maka menjawab pertanyaan ini bahkan lebih sulit karena kenyataan bahwa kurva dapat berisik (memiliki penyebaran poin besar).

Misalkan kita menambahkan ke grafik kita kurva ketergantungan dari besarnya kesalahan pada jumlah data dari sampel uji dan mendapat gambar berikut:

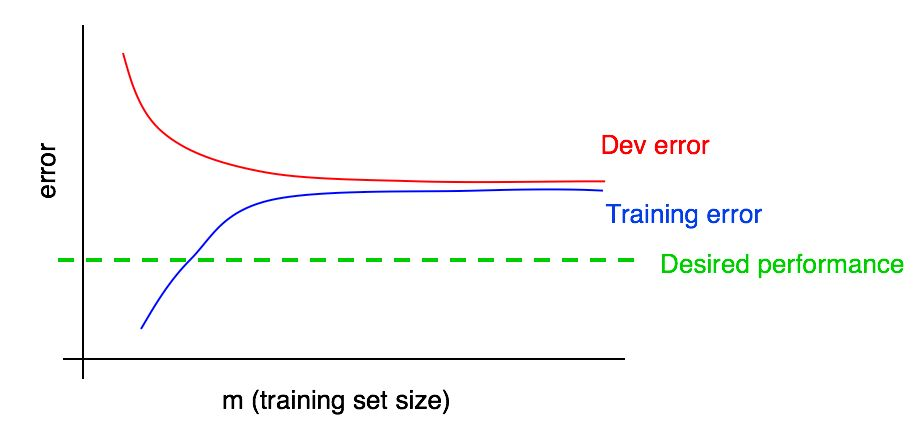
Dengan melihat dua kurva ini, Anda dapat benar-benar yakin bahwa menambahkan data baru saja tidak akan memberikan efek yang diinginkan (itu tidak akan memungkinkan untuk meningkatkan kualitas algoritma). Di mana kesimpulan ini bisa ditarik?
Mari kita ingat dua hal berikut:

• Jika kami menambahkan lebih banyak data ke set pelatihan, kesalahan algoritme di set pelatihan hanya dapat meningkat. Dengan demikian, garis biru bagan kami tidak akan berubah, atau akan merayap naik dan akan menjauh dari tingkat kualitas yang diinginkan dari algoritma kami (garis hijau).
• Garis kesalahan merah dalam sampel validasi biasanya lebih tinggi dari garis kesalahan biru algoritma dalam sampel pelatihan. Dengan demikian, dalam keadaan apa pun yang dapat dibayangkan, menambahkan data tidak akan menyebabkan penurunan lebih lanjut pada garis merah, itu tidak akan membawanya lebih dekat ke tingkat kesalahan yang diinginkan. Ini hampir mustahil, mengingat bahwa bahkan kesalahan dalam sampel pelatihan lebih tinggi dari yang diinginkan.

Pertimbangan kedua kurva dari ketergantungan kesalahan algoritma pada jumlah data dalam validasi dan sampel pelatihan pada grafik yang sama memungkinkan Anda untuk lebih percaya diri memperkirakan kurva kesalahan dari algoritma pembelajaran dari jumlah data dalam sampel validasi.

Misalkan kita memiliki perkiraan kualitas algoritma yang diinginkan dalam bentuk tingkat kesalahan optimal di sistem kita. Dalam kasus ini, grafik di atas adalah ilustrasi dari kasus "buku teks" standar tentang bagaimana kurva belajar terlihat dengan tingkat bias dilepas yang tinggi. Pada ukuran sampel pelatihan terbesar, mungkin sesuai dengan semua data yang kami miliki, ada celah besar antara kesalahan algoritma dalam sampel pelatihan dan kualitas algoritma yang diinginkan, yang menunjukkan tingkat bias yang tinggi dihindari. Selain itu, kesenjangan antara kesalahan dalam sampel pelatihan dan kesalahan dalam sampel validasi kecil, yang menunjukkan penyebaran kecil.

Sebelumnya, kami membahas kesalahan algoritma yang dilatih pada sampel pelatihan dan validasi hanya pada titik paling kanan di atas grafik, yang sesuai dengan penggunaan semua data pelatihan yang kami miliki. Kurva dependensi kesalahan pada jumlah data dari sampel pelatihan, dibangun untuk berbagai ukuran sampel yang digunakan untuk pelatihan, memberi kita gambaran yang lebih lengkap tentang kualitas algoritma yang dilatih pada berbagai ukuran sampel pelatihan.

31. Interpretasi Kurva Belajar: Kasus-Kasus Lain

Pertimbangkan kurva pembelajaran:

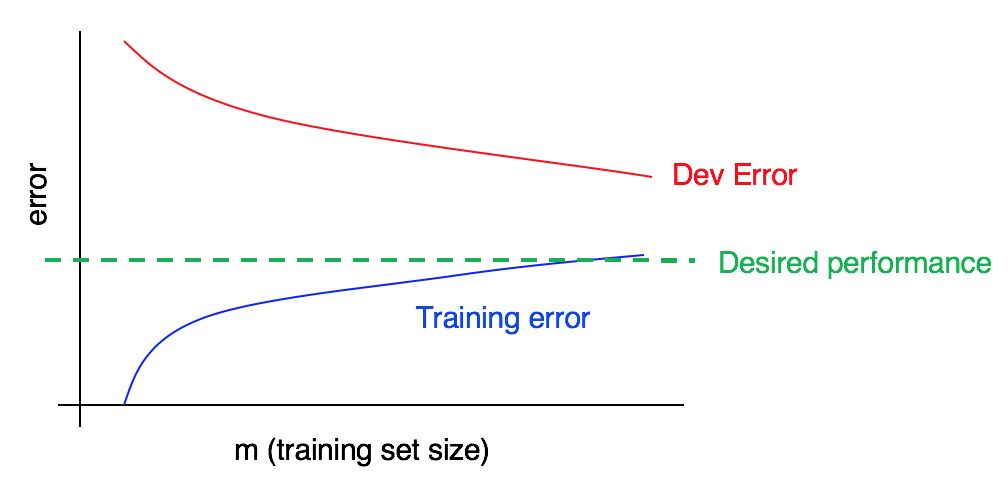
Apakah ada bias tinggi, penguraian tinggi, atau keduanya sekaligus?

Kurva kesalahan biru pada data pelatihan relatif rendah, kurva kesalahan merah pada data validasi secara signifikan lebih tinggi daripada kesalahan biru pada data pelatihan. Jadi, dalam hal ini, biasnya kecil, tetapi penyebarannya besar. Menambahkan lebih banyak data pelatihan dapat membantu menutup kesenjangan antara kesalahan dalam sampel validasi dan kesalahan dalam sampel pelatihan.

Sekarang perhatikan grafik ini:

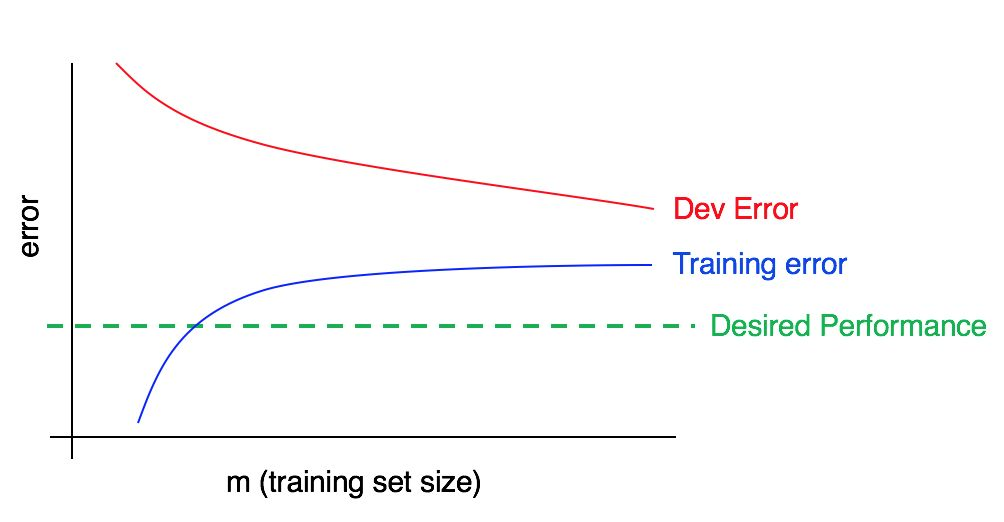
Dalam hal ini, kesalahan dalam sampel pelatihan besar, secara signifikan lebih tinggi dari algoritma yang sesuai dengan tingkat kualitas yang diinginkan. Kesalahan dalam sampel validasi juga jauh lebih tinggi daripada kesalahan dalam sampel pelatihan. Dengan demikian, kita berhadapan dengan bias dan pencar yang besar secara bersamaan. Anda harus mencari cara untuk mengurangi dan mengimbangi dan membubarkan algoritma Anda.

32. Membangun kurva belajar

Misalkan Anda memiliki sampel pelatihan yang sangat kecil, yang hanya terdiri dari 100 contoh. Anda melatih algoritme Anda menggunakan subset yang dipilih secara acak dari 10 contoh, kemudian dari 20 contoh, kemudian dari 30 dan seterusnya menjadi 100, meningkatkan jumlah contoh dengan interval sepuluh contoh. Kemudian menggunakan 10 poin ini Anda membangun kurva belajar Anda. Anda mungkin menemukan bahwa kurva tampak berisik (nilai lebih tinggi atau lebih rendah dari yang diharapkan) untuk sampel pelatihan yang lebih kecil.

Ketika Anda melatih algoritme dengan hanya 10 contoh yang dipilih secara acak, Anda mungkin tidak beruntung dan ini akan berubah menjadi pelatihan subsampel yang “buruk” dengan bagian yang lebih besar dari contoh yang ambigu / ditandai dengan tidak tepat. Atau, sebaliknya, Anda bisa menemukan subsampel pelatihan yang “bagus”. Kehadiran sampel pelatihan kecil menyiratkan bahwa nilai kesalahan dalam validasi dan sampel pelatihan dapat dikenakan fluktuasi acak.

Jika data yang digunakan untuk aplikasi Anda menggunakan pembelajaran mesin sangat condong ke satu kelas (seperti dengan masalah klasifikasi kucing, di mana proporsi contoh negatif jauh lebih besar daripada proporsi positif), atau jika kita berurusan dengan sejumlah besar kelas (seperti pengakuan terhadap 100 spesies hewan yang berbeda), maka kesempatan untuk mendapatkan sampel pelatihan yang “tidak representatif” atau buruk juga meningkat. Sebagai contoh, jika 80% dari contoh Anda adalah contoh negatif (y = 0), dan hanya 20% adalah contoh positif (y = 1), maka ada kemungkinan bahwa subset pelatihan dari 10 contoh hanya akan berisi contoh negatif, dalam hal ini sangat sulit untuk mendapatkan sesuatu yang masuk akal dari algoritma yang dilatih.

Jika, karena kebisingan dari kurva pembelajaran dalam sampel pelatihan, sulit untuk membuat penilaian tren, seseorang dapat mengusulkan dua solusi berikut:

• Alih-alih melatih hanya satu model untuk 10 contoh pelatihan, memilih dengan mengganti beberapa (katakanlah 3 hingga 10) subsampel pelatihan acak yang berbeda dari sampel awal yang terdiri dari 100 contoh. Latih model pada masing-masing dari mereka dan hitung untuk masing-masing model ini kesalahan pada validasi dan sampel pelatihan. Hitung dan plot rata-rata kesalahan pada sampel pelatihan dan validasi.

  
  

  Komentar penulis: Sampel dengan pengganti berarti yang berikut: pilih secara acak 10 contoh pertama yang berbeda dari 100 untuk membentuk subsampel pelatihan pertama. Kemudian, untuk membentuk subsampel pelatihan kedua, sekali lagi kami mengambil 10 contoh, tetapi tanpa memperhitungkan yang dipilih dalam subsampel pertama (sekali lagi dari keseluruhan seratus contoh). Dengan demikian, satu contoh spesifik dapat muncul di kedua sub-sampel. Ini membedakan sampel dengan penggantian dari sampel tanpa penggantian, dalam hal sampel tanpa penggantian, subsampel pelatihan kedua akan dipilih dari hanya 90 contoh yang tidak termasuk dalam subsampel pertama. Dalam praktiknya, metode pemilihan contoh dengan atau tanpa substitusi seharusnya tidak terlalu penting, tetapi pemilihan contoh dengan substitusi adalah praktik umum.

  
  

• Jika sampel pelatihan Anda condong ke salah satu kelas, atau jika itu mencakup banyak kelas, pilih subsampel “seimbang” yang terdiri dari 10 contoh pelatihan, dipilih secara acak dari 100 sampel sampel. Misalnya, Anda dapat yakin bahwa 2/10 contoh positif dan 8/10 negatif. Untuk meringkas, Anda dapat yakin bahwa proporsi contoh setiap kelas dalam kumpulan data yang diamati sedekat mungkin dengan bagian mereka dalam sampel pelatihan awal.

  
  

  Saya tidak akan repot dengan salah satu dari metode ini sampai grafik kurva kesalahan mengarah pada kesimpulan bahwa kurva ini terlalu berisik, yang tidak memungkinkan kita untuk melihat tren yang dapat dimengerti. Jika Anda memiliki sampel pelatihan besar - misalkan 10.000 contoh dan distribusi kelas Anda tidak terlalu bias, Anda mungkin tidak memerlukan metode ini.

  
  

Akhirnya, membangun kurva belajar bisa mahal dari sudut pandang komputasi: Misalnya, Anda perlu melatih sepuluh model, dalam 1000 contoh pertama, pada 2000 kedua, dan seterusnya sampai yang terakhir yang berisi 10.000 contoh. Pelatihan model pada sejumlah kecil data jauh lebih cepat daripada pelatihan model pada sampel besar. Dengan demikian, alih-alih mendistribusikan ukuran sampel pelatihan secara merata dalam skala linier, seperti dijelaskan di atas (1000, 2000, 3000, ..., 10000), Anda dapat melatih model dengan peningkatan non-linear dalam jumlah contoh, misalnya, 1000, 2000, 4000, 6000 dan 10.000 contoh. Semua sama, itu harus memberi Anda pemahaman yang jelas tentang tren ketergantungan kualitas model pada jumlah contoh pelatihan dalam kurva belajar. Tentu saja, teknik ini hanya relevan jika biaya komputasi untuk pelatihan model tambahan tinggi.

kelanjutan