🏂🏼 🌳 🛀🏼 Sortasi Hibrid ⬅️ ♀️ 👁‍🗨

Seperti yang sudah diketahui semua orang, penyortiran dapat didasarkan pada pertukaran, sisipan, pemilihan, penggabungan, dan distribusi.

Tetapi jika metode yang berbeda digabungkan dalam algoritma, maka itu milik kelas macam hibrida.

Artikel ini ditulis dengan dukungan EDISON.

Kami terlibat dalam penyelesaian dan pemeliharaan situs di 1C-Bitrix , serta pengembangan aplikasi mobile Android dan iOS .

Kami menyukai teori algoritma! ;-)

Mari kita cepat mengingat apa yang dimiliki algoritma pengurutan kelas dan apa saja fitur masing-masing.

Pertukaran macam

Elemen-elemen array dibandingkan berpasangan satu sama lain dan pertukaran dibuat untuk pasangan yang tidak teratur.

Perwakilan paling efektif dari kelas ini adalah jenis cepat legendaris.

Urutan Penyisipan

Elemen dari bagian array yang tidak disortir dimasukkan ke dalam tempatnya di area yang diurutkan.

Dari kelas ini, menyortir berdasarkan sisipan sederhana paling sering digunakan. Meskipun algoritma ini memiliki kompleksitas rata-rata O ( n ² ), pengurutan ini bekerja sangat cepat dengan array yang hampir teratur - pada mereka kompleksitas mencapai O ( n ). Selain itu, pengurutan ini adalah salah satu opsi terbaik untuk memproses array kecil.

Mengurutkan menggunakan pohon pencarian biner juga termasuk dalam kelas ini.

Sortir berdasarkan pilihan

Di area tidak berurutan, elemen minimum / maksimum dipilih, yang ditransfer ke akhir / awal bagian array yang tidak disortir.

Penyortiran dengan pilihan sederhana bekerja sangat lambat (rata-rata O ( n ² )), tetapi di kelas ini ada penyortiran yang sulit dengan tumpukan (alias penyortiran piramidal ), yang memiliki kompleksitas waktu O ( n log n ) - dan, yang sangat berharga, Tidak ada kasus degenerasi penyortiran ini, apa pun data yang masuk. Ngomong-ngomong, pengurutan ini juga tidak memiliki kasus terbaik untuk data yang masuk.

Gabungkan Urusan

Area yang diurutkan diambil dalam array dan digabung, yaitu, subarrays yang lebih kecil digabungkan menjadi subarray yang lebih besar.

Jika dua subarrays diurutkan, maka menggabungkannya adalah operasi yang mudah diimplementasikan dan waktu cepat. Sisi lain dari koin adalah bahwa penggabungan hampir selalu membutuhkan biaya memori tambahan O ( n ) - walaupun ada beberapa opsi yang sangat canggih untuk menyortir dengan penggabungan, di mana biaya memori adalah O (1).

Urutkan berdasarkan distribusi

Elemen-elemen dari array didistribusikan dan didistribusikan kembali ke dalam kelas sampai array menerima keadaan yang diurutkan.

Elemen-elemen tersebar ke dalam kelompok baik tergantung pada nilainya (apa yang disebut sorting penghitungan ) atau tergantung pada nilai digit individu (ini sudah sortasi bitwise ).

Penyortiran ember juga termasuk dalam kelas ini.

Ciri pengurutan berdasarkan distribusi adalah bahwa keduanya tidak menggunakan perbandingan elemen berpasangan di antara mereka sendiri, atau perbandingan semacam itu hanya ada pada tingkat yang kecil. Oleh karena itu, pengurutan berdasarkan distribusi seringkali lebih cepat, misalnya, pengurutan cepat. Di sisi lain, pengurutan berdasarkan distribusi seringkali membutuhkan banyak memori tambahan, karena kelompok elemen yang terus-menerus didistribusikan perlu disimpan di suatu tempat.

Perselisihan tentang penyortiran mana yang terbaik adalah sangat sering, tetapi faktanya adalah bahwa tidak ada dan tidak bisa menjadi algoritma yang ideal untuk semua kesempatan. Misalnya, penyortiran cepat sangat cepat (tapi bukan yang tercepat) di sebagian besar situasi, tetapi penyortiran juga terjadi pada kasus yang merosot saat terjadi kerusakan. Menyortir berdasarkan sisipan sederhana lambat, tetapi untuk array yang hampir dipesan, akan dengan mudah mem-bypass algoritma lain. Heap sorting bekerja cukup cepat dengan data yang masuk, tetapi tidak secepat sortasi lainnya dalam kondisi tertentu dan tidak ada cara untuk mempercepat piramida. Menggabungkan pengurutan lebih lambat dari pengurutan cepat, namun jika ada diurutkan sub-array dalam array, maka lebih cepat untuk menggabungkan mereka daripada mengurutkan dengan pengurutan cepat. Jika array memiliki banyak elemen berulang atau kita mengurutkan baris, maka kemungkinan besar mengurutkan berdasarkan distribusi adalah pilihan terbaik. Setiap metode sangat baik dalam situasi yang paling menguntungkan.

Meskipun demikian, programmer terus menciptakan sortasi tercepat di dunia, mensintesis metode paling efektif dari kelas yang berbeda. Mari kita lihat seberapa sukses itu untuk mereka.

Karena banyak algoritma non-sepele disebutkan dalam artikel, saya hanya membahas secara singkat prinsip-prinsip dasar pekerjaan mereka, tanpa membebani artikel dengan animasi dan penjelasan rinci. Di masa depan akan ada artikel terpisah, di mana akan ada kartun untuk setiap algoritma dan nuansa halus yang terperinci.

Sisipkan + Gabung

Kesimpulan murni empiris adalah bahwa fusi dan / atau penyisipan paling sering digunakan dalam hibrida. Dalam sebagian besar penyortiran, satu atau metode lain ditemukan, atau keduanya bersamaan. Dan ada penjelasan logis untuk ini.

Sortir penemu sering berusaha untuk membuat algoritma paralel yang secara bersamaan memesan berbagai bagian array. Cara terbaik untuk menangani beberapa subarrays yang diurutkan adalah dengan menggabungkannya - ini akan menjadi yang tercepat.

Algoritma modern sering menggunakan rekursi. Selama turunan rekursif, array biasanya dibagi menjadi dua bagian, pada level terendah, array dipesan. Ketika kembali ke level rekursi yang lebih tinggi, muncul pertanyaan menggabungkan sub-array yang diurutkan pada level yang lebih rendah.

Sedangkan untuk sisipan, dalam algoritma hibrid pada tahap tertentu sering kira-kira sub-susunan pesanan diperoleh, yang terbaik mengarah pada pemesanan akhir dengan bantuan sisipan.

Grup ini berisi jenis hibrid, di mana ada penggabungan dan penyisipan, dan metode ini digunakan sangat berbeda.

Sortir penggabungan-penyisipan
Algoritma Ford Johnson :: Algoritma Ford-Johnson

Gabung + Sisipkan

Cara yang sangat kuno, sudah di tahun 1959. Hal ini dijelaskan secara terperinci dalam karya abadi Donald Knuth, “Seni Pemrograman,” Volume 3, “Penyortiran dan Pencarian,” Bab 5, “Penyortiran,” Bagian 5.3, “Penyortiran Optimal,” subbagian, “Penyortiran dengan Jumlah Minimum Perbandingan,” dan bagian “Penyortiran dengan Penyisipan dan Penggabungan”. .

Penyortiran sekarang tidak memiliki nilai praktis, tetapi menarik bagi mereka yang menyukai teori algoritma. Masalah menemukan cara untuk mengurutkan n elemen dengan jumlah perbandingan paling sedikit dipertimbangkan. Modifikasi heuristik non-sepele penyortiran penyisipan (penyisipan Anda tidak akan menemukan tempat lain) menggunakan nomor Jacobstal diusulkan untuk meminimalkan jumlah perbandingan. Sampai saat ini, juga diketahui bahwa ini bukan pilihan terbaik dan Anda bahkan bisa dengan lebih cekatan menghindari dan mendapatkan lebih sedikit perbandingan. Secara umum, penyortiran akademik standar tidak berguna secara praktis, tetapi bagi para pecinta genre, senang membongkar trik semacam itu dengan bias aljabar.

Sortir Tim :: Timsort

Sisipkan + Gabung

Diposting oleh Tim Peters 15 tahun yang lalu dan sekarang

Penyortiran Habré seperti ini sering diingat.
Tesis: dalam sebuah array, sub-array kecil yang hampir dipesan dicari untuk menyortir penyisipan yang digunakan. Subarrays ini kemudian digabung menggunakan gabungan.

Penggabungan dalam TimSort adalah bagian yang paling menarik: penggabungan ke atas klasik lebih dioptimalkan untuk situasi yang berbeda. Misalnya, diketahui bahwa penggabungan lebih efisien jika subarrays yang digabung kira-kira berukuran sama. Di TimSort, jika ukurannya sangat berbeda, maka setelah tindakan tambahan ada penyesuaian (kita dapat mengatakan bahwa bagian dari elemen akan "mengalir" dari subarray yang lebih besar ke yang lebih kecil, setelah penggabungan akan dilanjutkan dalam mode standar). Berbagai situasi berbahaya juga disediakan - misalnya, jika dalam satu subarray semua elemen akan kurang dari yang lain. Dalam hal ini, perbandingan elemen-elemen dari kedua sub-layar akan menganggur. Prosedur merger yang dimodifikasi akan "memperhatikan" perkembangan peristiwa yang tidak diinginkan pada waktunya, dan jika "yakin" akan opsi pesimistis menggunakan pencarian biner, ia akan beralih ke opsi pemrosesan yang lebih optimal.

Rata-rata, pengurutan ini bekerja sedikit lebih lambat daripada QuickSort, namun, jika array yang masuk berisi jumlah yang cukup dari urutan elemen berikutnya, maka kecepatan meningkat secara signifikan dan di sini TimSort lebih maju dari yang lain.

Block merge sort :: Blok merge sort
Wiki-sort :: Wiki-sort
Holy Grail Sort :: Grailsort

Sisipan + Gabung + Bucket

Blokir animasi penyortiran gabungan dari Wikipedia.

Ini sangat segar (2008) dan pada saat yang sama algoritma yang sangat menjanjikan. Faktanya adalah bahwa masalah penggabungan yang relatif signifikan adalah biaya memori tambahan. Biasanya, di mana penggabungan ada, ada juga kompleksitas memori O ( n ).

Tetapi WikiSort dirancang agar penggabungan terjadi tanpa menggunakan memori tambahan - di antara jenis penggabungan, dalam hal ini, ini adalah contoh yang sangat jarang. Selain itu, algoritma ini stabil. Nah, jika sorting gabungan konvensional memiliki kecepatan algoritmik terbaik O ( n log n ), maka dalam wiki sorting indikator ini adalah O ( n ). Sampai baru-baru ini, pada prinsipnya diyakini bahwa menggabungkan penyortiran dengan seperangkat karakteristik seperti itu tidak mungkin, tetapi programmer Cina mengejutkan semua orang.

Algoritma ini sangat rumit untuk dijelaskan dalam beberapa kalimat. Tapi suatu hari nanti aku akan menulis kebiasaan berbeda tentang dia.

Awalnya, algoritma itu tanpa nama disebut Block Merge Sort, namun, dengan tangan ringan Tim Peters, yang mempelajari penyortiran secara detail (untuk menentukan apakah beberapa idenya harus ditransfer ke TimSort), nama WikiSort melekat padanya.

Habruiser yang berangkat sebelum waktunya secara independen bekerja selama beberapa tahun untuk menyortir gabungan, yang secara bersamaan cepat dengan data yang masuk, ekonomis dalam memori, dan stabil. Pencarian kreatifnya berhasil dan dia kemudian menyebut algoritma yang dikembangkan sebagai penyortiran Holy Grail (karena memenuhi semua persyaratan tinggi "penyortiran sempurna"). Sebagian besar ide dari algoritma ini mirip dengan yang diterapkan di WikiSort, meskipun jenis ini tidak identik dan dikembangkan secara independen satu sama lain.

Sortir tabel hash :: Sortir tabel hash

Distribusi + Sisipkan + Gabung

Array secara rekursif dibagi menjadi dua, sampai jumlah elemen dalam subarrays yang dihasilkan mencapai nilai ambang tertentu. Pada tingkat rekursi terendah, perkiraan distribusi terjadi (menggunakan tabel hash) dan subarray diurutkan berdasarkan sisipan. Lalu ada pengembalian rekursif ke tingkat yang lebih tinggi, bagian yang diurutkan dikombinasikan dengan penggabungan.

Saya berbicara sedikit lebih banyak tentang algoritma ini sebulan yang lalu .

Sortir cepat sebagai primer

Setelah menggabungkan dan menyisipkan, tempat ketiga dalam parade hit hibrida dipegang teguh oleh jenis cepat favorit semua orang.

Ini adalah algoritma yang sangat efisien, tetapi ada kasus yang merosot untuk itu juga. Beberapa penemu mencoba membuat QuickSort benar-benar kebal terhadap data masuk yang buruk dan menyarankan untuk melengkapi dengan ide-ide kuat dari jenis lain.

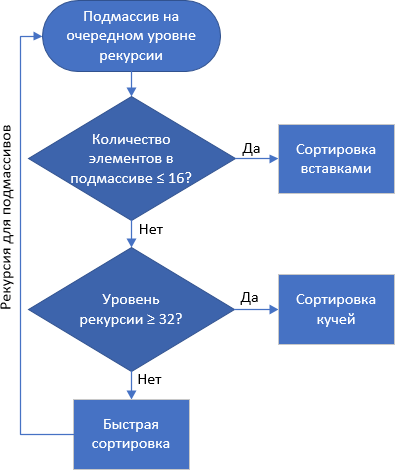
Sortir introspektif :: Introsort, Introspektif sort, std :: sort

Sisipan + heap + cepat

Heap sorting bekerja lebih lambat daripada sortasi cepat, tetapi pada saat yang sama, tidak seperti QuickSort, ia tidak memiliki kasus yang merosot - rata-rata, kompleksitas waktu algoritmik algoritme terbaik dan terburuk adalah O ( n log n ).

Oleh karena itu, David Musser mengusulkan untuk aman selama penyortiran cepat - jika ada tingkat sarang yang terlalu tinggi, maka ini dianggap sebagai serangan pada sistem, yang menyelipkan array yang "buruk". Beralih ke pengurutan berdasarkan tumpukan terjadi, yang bukan megabyte, tetapi juga tidak lambat untuk mengatasi data yang masuk.

C ++ memiliki algoritma yang disebut std :: sort, yang merupakan implementasi dari penyortiran introspektif. Tambahan kecil - jika pada tingkat rekursi berikutnya jumlah elemen subarray adalah ≤ 16 , maka penyortiran penyisipan diterapkan ke subarray.

Urut multikey :: Urut multikey
Bitwise Quick Sort :: Radix quick sort

Peringkat + cepat

Penyortiran cepat, hanya nilai-nilai elemen array yang dibandingkan satu sama lain, tetapi masing-masing digit (pertama, kami memesan digit yang lebih tinggi dengan cara ini, kami bergerak dari yang terendah).

Atau lebih - ini pengurutan bitwise dengan urutan tinggi, pemesanan di dalam bit berikutnya dilakukan sesuai dengan algoritma pengurutan cepat.

Sortir Menyebar :: Spreadsort

Cepat + gabungkan + ember + pelepasan

Gestalt dari quicksort, merge sort, sort ember, dan bitwise sort.

Singkatnya, jangan menjelaskan. Kami akan menganalisis algoritme ini secara rinci di salah satu artikel berikut.

Hibrida lainnya

Jenis penghitungan pohon

Menghitung + pohon

Algoritma yang diajukan oleh pengguna AlexanderUsatov . Jenis penghitungan, jumlah kunci yang dihitung disimpan di pohon seimbang.

J-sort :: J-sort

Sisipan tumpukan +

Saya sudah menulis tentang penyortiran ini 5 tahun yang lalu . Semuanya cukup sederhana - pertama dalam array Anda perlu membangun heap yang tidak bertambah sekali, dan kemudian melakukan yang sebaliknya - membangun yang tidak berkurang sekali. Sebagai hasil dari operasi pertama, minimum akan berada di tempat pertama array, dan elemen-elemen kecil secara keseluruhan akan secara signifikan pindah ke awal. Dalam kasus kedua, maksimum akan berada di tempat terakhir, dan elemen besar bermigrasi ke akhir array. Secara umum, kita mendapatkan array yang hampir diurutkan dengan apa yang kita lakukan? Benar - bereskan sisipan.