Teori Informasi Visual (Bagian 1)

Terjemahan dari longread yang menarik dikhususkan untuk visualisasi konsep dari teori informasi. Pada bagian pertama, kita akan melihat bagaimana secara grafis mewakili distribusi probabilitas, interaksinya, dan probabilitas kondisional. Selanjutnya, kita akan membahas kode panjang tetap dan variabel, melihat bagaimana kode optimal dibuat dan mengapa demikian. Sebagai pelengkap, paradoks statistik Simpson dipahami secara visual.

Teori informasi memberi kita bahasa yang akurat untuk menggambarkan banyak hal. Berapa banyak ketidakpastian dalam diri saya? Berapa banyak pengetahuan tentang jawaban pertanyaan A yang memberi tahu saya tentang jawaban pertanyaan B? Seberapa miripkah satu set kepercayaan dengan yang lainnya? Saya memiliki versi informal dari ide-ide ini ketika saya masih kecil, tetapi teori informasi mengkristalkannya menjadi ide-ide yang tepat dan kuat. Ide-ide ini memiliki beragam aplikasi, mulai dari kompresi data hingga fisika kuantum, pembelajaran mesin, dan area luas di antaranya.

Sayangnya, teori informasi bisa tampak menakutkan. Saya kira tidak ada alasan untuk ini. Bahkan, banyak ide kunci dapat dijelaskan secara visual!

Visualisasi Distribusi Peluang

Sebelum kita mempelajari teori informasi, mari kita pikirkan bagaimana Anda dapat memvisualisasikan distribusi probabilitas sederhana. Kita akan membutuhkannya nanti, di samping itu, teknik-teknik untuk memvisualisasikan probabilitas berguna dalam diri mereka sendiri!

Saya di California. Kadang hujan, tapi kebanyakan matahari! Katakanlah, 75% dari waktu cerah. Sangat mudah untuk digambarkan dalam gambar:


Hampir setiap hari saya memakai T-shirt, tapi kadang-kadang saya memakai jas hujan. Misalkan saya memakai jas hujan 38% dari waktu. Ini juga mudah untuk digambarkan.


Bagaimana jika saya ingin memvisualisasikan kedua fakta secara bersamaan? Sangat sederhana jika mereka tidak berinteraksi - yaitu independen. Misalnya, jika itu: bahwa saya mengenakan T-shirt atau jas hujan hari ini tidak tergantung pada cuaca minggu depan. Kami dapat menggambarkan ini menggunakan satu sumbu untuk satu variabel dan satu untuk yang lain:



Perhatikan garis lurus vertikal dan horizontal. Seperti inilah kemandirian! Kemungkinan saya memakai jas hujan tidak akan berubah karena dalam seminggu hujan akan turun. Dengan kata lain, probabilitas bahwa saya akan mengenakan jas hujan dan bahwa akan hujan minggu depan sama dengan probabilitas bahwa saya akan memakai jas hujan dikali probabilitas bahwa itu akan hujan. Mereka tidak berinteraksi.

Ketika variabel berinteraksi, probabilitas dapat meningkat untuk beberapa pasang variabel dan menurun untuk yang lain. Ada kemungkinan besar bahwa saya memakai jas hujan dan hujan karena variabelnya berkorelasi, mereka membuat satu sama lain lebih mungkin. Lebih mungkin saya memakai jas hujan pada hari hujan daripada kemungkinan saya memakai jas hujan pada suatu hari dan hujan pada hari acak lainnya.

Secara visual, sepertinya beberapa kotak membengkak dengan probabilitas tambahan, sementara kotak lainnya menyempit, karena beberapa peristiwa tidak mungkin terjadi secara bersamaan:



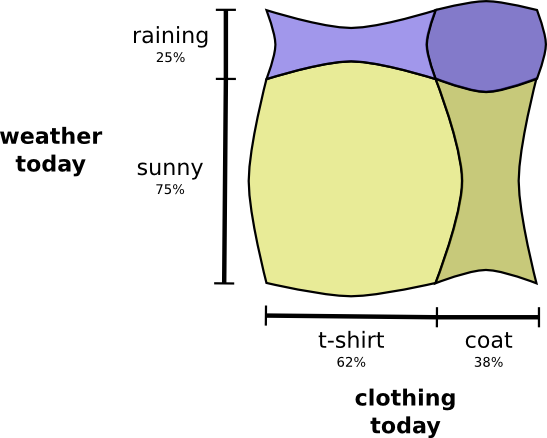
Tetapi meskipun terlihat keren, tidak terlalu berguna untuk memahami apa yang terjadi.

Sebagai gantinya, mari kita fokus pada variabel seperti cuaca. Kita tahu probabilitas cuaca cerah dan hujan. Dalam kedua kasus, kami dapat mempertimbangkan probabilitas bersyarat. Apa kemungkinan saya akan mengenakan T-shirt jika cerah? Apa kemungkinan saya akan memakai jas hujan jika hujan?


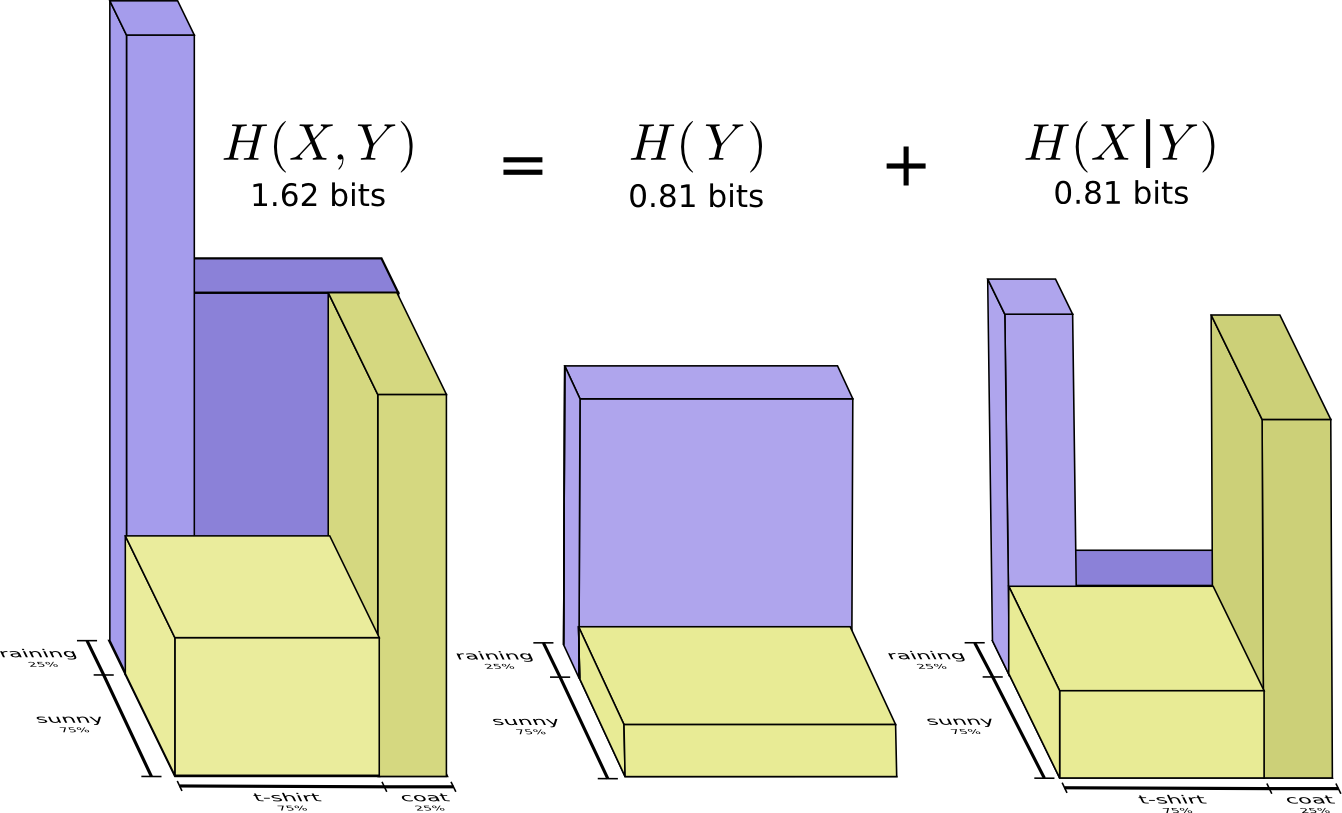
Dengan probabilitas 25%, hujan akan turun. Jika hujan, saya akan mengenakan jas hujan dengan peluang 75%. Jadi, kemungkinan hujan dan saya memakai jas hujan adalah 25% dari 75%, yaitu sekitar 19%. Probabilitas hujan dan saya mengenakan jas hujan adalah probabilitas hujan turun dikalikan dengan probabilitas bahwa saya akan memakai jas hujan jika hujan. Kami menulis seperti ini:

$$

$$p (hujan, mantel) = p (hujan) ⋅p (mantel | hujan)$$

Ini adalah contoh dari salah satu identitas paling mendasar dari teori probabilitas:

$$

$$p (x, y) = p (x) ⋅p (y | x)$$

Kami memfaktorkan distribusi dengan memecahnya menjadi produk dua bagian. Pertama, kita melihat probabilitas bahwa satu variabel, cuaca, akan mengambil nilai tertentu. Kemudian kita melihat kemungkinan bahwa variabel lain, pakaian saya, akan mengambil nilai karena variabel pertama.

Variabel mana untuk memulai dengan tidak masalah. Kita bisa mulai dengan pakaian saya, dan kemudian melihat cuaca yang disebabkan oleh ini. Ini mungkin tampak kurang intuitif karena kita memahami bahwa ada hubungan sebab akibat antara cuaca yang memengaruhi apa yang saya kenakan dan bukan sebaliknya ... tetapi itu tetap berhasil!

Mari kita lihat sebuah contoh. Jika kita memilih hari acak, dengan probabilitas 38% saya akan memakai jas hujan. Jika kita tahu saya memakai jas hujan, seberapa besar kemungkinan hujan? Saya lebih suka memakai jas hujan di bawah hujan daripada di bawah sinar matahari, tetapi hujan di California jarang, dan ternyata dengan kemungkinan 50% hujan akan turun. Jadi, kemungkinan hujan dan saya memakai jas hujan adalah probabilitas bahwa saya akan memakai jas hujan (38%), dikalikan dengan probabilitas hujan akan turun jika saya memakai jas hujan (50%), yaitu sekitar 19%.

$$

$$p (hujan, mantel) = p (mantel) ⋅p (hujan | mantel)$$

Ini memberi kita cara kedua untuk memvisualisasikan distribusi probabilitas yang sama.


Harap dicatat bahwa nilai label memiliki arti yang sedikit berbeda dari diagram sebelumnya: t-shirt dan jas hujan sekarang adalah probabilitas batas, probabilitas bahwa saya akan mengenakan pakaian ini tanpa memperhitungkan cuaca. Di sisi lain, sekarang ada dua tanda hujan dan matahari, karena probabilitas mereka tergantung pada kenyataan bahwa saya akan mengenakan T-shirt atau jas hujan.

(Anda mungkin pernah mendengar teorema Bayes. Anda dapat membayangkannya sebagai cara transisi antara dua cara berbeda untuk mewakili distribusi probabilitas!)

Kotak: Paradoks Simpson

Apakah teknik visualisasi ini untuk distribusi probabilitas benar-benar bermanfaat? Saya kira begitu! Sedikit lebih jauh, kita menggunakannya untuk memvisualisasikan teori informasi, tetapi untuk sekarang kita menggunakannya untuk mempelajari paradoks Simpson. Paradoks Simpson adalah situasi statistik yang sangat tidak intuitif. Sulit dipahami pada tingkat intuitif. Michael Nielsen menulis esai Reinventing Explanation yang sangat baik, yang menjelaskan paradoks dalam banyak hal. Saya ingin mencoba melakukannya sendiri, menggunakan teknik yang kami kembangkan di bagian sebelumnya.

Dua metode untuk mengobati batu ginjal sedang diuji. Setengah dari pasien menerima pengobatan A, sedangkan setengah lainnya menerima pengobatan B. Pasien yang menerima pengobatan B lebih mungkin untuk pulih daripada mereka yang menerima pengobatan A.


Namun, pasien dengan batu ginjal kecil lebih mungkin untuk pulih jika mereka menerima pengobatan A. Pasien dengan batu ginjal besar di ginjal juga lebih mungkin untuk pulih jika mereka menerima pengobatan A! Bagaimana ini bisa terjadi?

Inti dari masalah adalah bahwa penelitian ini tidak diacak dengan benar. Di antara pasien yang menerima pengobatan A, ada lebih banyak pasien dengan batu ginjal besar, dan di antara pasien yang menerima pengobatan B ada lebih banyak dengan batu ginjal kecil.


Ternyata, pasien dengan batu ginjal kecil lebih mungkin sembuh secara umum.

Untuk lebih memahami hal ini, kita dapat menggabungkan dua diagram sebelumnya. Hasilnya adalah grafik tiga dimensi dengan tingkat pemulihan dibagi menjadi batu ginjal kecil dan besar.


Sekarang kita melihat bahwa dalam kasus batu besar dan kecil, pengobatan A lebih unggul daripada pengobatan B. Pengobatan B terlihat lebih baik hanya karena pasien yang diaplikasikan memiliki, secara umum, lebih banyak peluang untuk pulih!

Kode

Sekarang kita memiliki cara untuk memvisualisasikan probabilitas, kita dapat menyelami teori informasi.

Biarkan saya memberi tahu Anda tentang teman khayalan saya, Bob. Bob sangat mencintai binatang. Dia terus berbicara tentang binatang. Bahkan, ia hanya berbicara empat kata: "anjing", "kucing", "ikan" dan "burung".

Beberapa minggu yang lalu, terlepas dari kenyataan bahwa Bob adalah bagian dari imajinasi saya, dia pindah ke Australia. Selain itu, dia memutuskan bahwa dia ingin berkomunikasi hanya dalam format biner. Semua pesan (imajiner) saya dari Bob terlihat seperti ini:


Untuk berkomunikasi, Bob dan saya perlu membuat sistem pengkodean - cara untuk menampilkan kata dalam urutan bit.


Untuk mengirim pesan, Bob mengganti setiap karakter (kata) dengan kata kode yang sesuai, lalu menggabungkan keduanya untuk membentuk string yang disandikan.

Kode Panjang Variabel

Sayangnya, layanan komunikasi di imajiner Australia mahal. Saya harus membayar $ 5 untuk setiap pesan yang saya terima dari Bob. Apakah saya menyebutkan bahwa Bob suka banyak bicara? Agar tidak bangkrut, Bob dan saya memutuskan untuk mencari tahu apakah mungkin untuk mengurangi panjang pesan rata-rata.

Ternyata Bob tidak sering mengucapkan semua kata dengan setara. Bob sangat mencintai anjing. Dia berbicara tentang anjing sepanjang waktu. Terkadang dia berbicara tentang binatang lain - terutama kucing yang suka dikejar anjingnya - tetapi kebanyakan dia berbicara tentang anjing. Berikut ini adalah grafik dari frekuensi kata-katanya:


Ini menggembirakan. Kode lama kami menggunakan kata-kata kode 2-bit, tidak peduli seberapa sering mereka digunakan.

Ada cara yang baik untuk memvisualisasikan ini. Dalam diagram berikut, kami menggunakan sumbu vertikal untuk memvisualisasikan probabilitas setiap kata $$$p (x)$dan sumbu horizontal untuk memvisualisasikan panjang kata sandi yang sesuai $$$L (x)$. Harap perhatikan bahwa area yang dihasilkan adalah panjang rata-rata kata kode yang kami kirim, dalam hal ini 2 bit.


Kita bisa lebih pintar dan membuat panjang kode variabel, di mana kata-kata kode untuk kata-kata umum dibuat lebih pendek. Masalahnya adalah bahwa ada persaingan antara codewords - membuat beberapa lebih pendek, kita dipaksa untuk membuat yang lain lebih lama. Untuk meminimalkan panjang pesan, idealnya kami ingin semua kata kode menjadi pendek, tetapi yang terpendek harus digunakan secara luas. Dengan demikian, kode yang dihasilkan berisi codewords yang lebih pendek untuk kata-kata umum (misalnya, "anjing") dan codewords yang lebih panjang untuk kata-kata langka (misalnya, "burung").


Mari kita visualisasikan ini lagi. Harap dicatat bahwa codeword yang paling umum lebih pendek dan paling langka lebih panjang. Akibatnya, kami mendapat area yang lebih kecil. Ini sesuai dengan panjang kode kata yang diharapkan lebih pendek. Panjang codeword rata-rata sekarang adalah 1,75 bit!



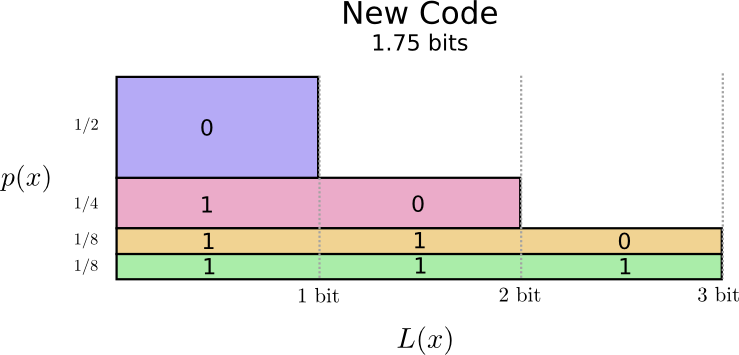
(Anda mungkin bertanya-tanya: mengapa tidak menggunakan 1 secara terpisah sebagai codeword? Sayangnya, ini akan menyebabkan ambiguitas ketika decoding string yang disandikan. Kami akan membicarakan lebih lanjut tentang ini sedikit kemudian.)

Ternyata kode ini adalah yang terbaik. Tidak ada kode untuk distribusi ini yang akan memberi kami panjang kata sandi rata-rata kurang dari 1,75 bit.

Ada batasan mendasar. Transmisi kata apa yang dikatakan, peristiwa distribusi mana yang terjadi, mengharuskan kita untuk mengirimkan rata-rata setidaknya 1,75 bit. Tidak peduli seberapa pintar kode kita, tidak mungkin untuk mencapai bahwa panjang pesan rata-rata kurang. Kami menyebut batas mendasar ini sebagai entropi distribusi - kami akan membahasnya secara lebih rinci di bawah ini.



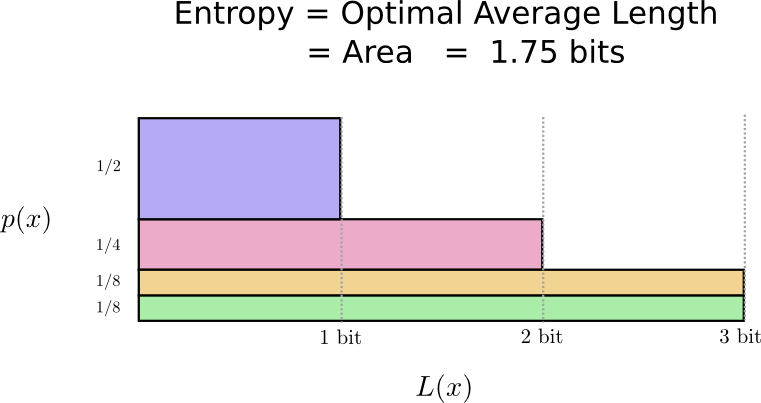
Jika kita ingin memahami batasan ini, kita perlu memahami pertukaran antara menjaga beberapa kata kode pendek dan yang lain panjang. Setelah kita mengetahui hal ini, kita dapat mencari tahu seperti apa sistem pengkodean terbaik yang mungkin terlihat.

Codeword Space

Ada dua codeword dengan panjang 1 bit: 0 dan 1. Ada empat codewords dengan panjang 2 bit: 00, 01, 10 dan 11. Setiap bit yang Anda tambahkan menggandakan jumlah kemungkinan codeword yang mungkin.


Kami tertarik pada kode panjang variabel, di mana beberapa kata kode lebih panjang dari yang lain. Kita dapat memiliki situasi sederhana ketika kita memiliki delapan codeword 3 bit. Mungkin ada campuran yang lebih kompleks, misalnya, dua codeword dengan panjang 2 dan empat codeword dengan panjang 3. Apa yang memutuskan berapa banyak codeword dengan panjang berbeda yang bisa kita miliki?

Ingat bahwa Bob mengubah pesannya menjadi string terenkripsi, mengganti setiap kata dengan kodenya dan menyatukannya.


Ada pertanyaan halus untuk berhati-hati saat membuat kode panjang variabel. Bagaimana kita membagi string yang disandikan kembali menjadi kata-kata kode? Ketika semua codeword memiliki panjang yang sama, mudah - cukup pisahkan string menjadi potongan-potongan sepanjang itu. Tetapi karena ada codeword dari berbagai panjang, kita perlu memperhatikan isinya.

Kami ingin kode kami didekodekan secara unik. Dan kami tidak ingin ambigu dalam menentukan codeword mana yang membentuk string yang disandikan. Jika kita memiliki simbol khusus "akhir kata kode", itu akan sederhana. Tetapi kami tidak memilikinya - kami hanya mengirim 0 dan 1. Kami harus dapat melihat urutan kata-kata kode dan menentukan di mana masing-masing berakhir.

Sangat mudah untuk membuat kode yang tidak dapat didekripsi secara jelas. Sebagai contoh, bayangkan 0 dan 01 keduanya merupakan kata sandi. Maka tidak jelas apa codeword pertama dari baris 0100111 adalah - bisa jadi ini atau itu! Properti yang kita butuhkan adalah bahwa jika kita melihat codeword tertentu, itu tidak boleh dimasukkan dalam codeword lain yang lebih panjang. Dengan kata lain, tidak ada codeword yang harus menjadi awalan dari codeword lain. Ini disebut properti awalan, dan kode yang mematuhinya disebut kode awalan .

Cara yang berguna untuk mewakili hal ini adalah bahwa setiap codeword membutuhkan pengorbanan dari ruang yang memungkinkan codeword. Jika kita mengambil kata kode 01, kita kehilangan kemampuan untuk menggunakan kata-kata kode apa pun yang awalannya. Kita tidak bisa lagi menggunakan 010 atau 011010110 karena ambiguitas - mereka hilang untuk kita.


Karena seperempat dari semua codeword dimulai pada 01, kami menyumbangkan seperempat dari semua codewords yang mungkin. Berikut adalah harga yang kami bayar sebagai ganti fakta bahwa kami memiliki satu codeword dengan panjang hanya 2 bit! Pada gilirannya, pengorbanan ini berarti bahwa semua codeword lainnya harus sedikit lebih panjang. Selalu ada semacam kompromi antara panjang codeword yang berbeda. Sebuah codeword pendek mengharuskan Anda mengorbankan sebagian besar ruang dari codewords yang mungkin, yang mencegah singkatnya codeword lainnya. Yang perlu kita ketahui adalah bagaimana berkompromi dengan benar!

Pengkodean optimal

Anda dapat menganggapnya sebagai anggaran terbatas yang dapat Anda pakai untuk mendapatkan kata-kata kode pendek. Kami membayar untuk satu codeword, mengorbankan sebagian dari codeword yang mungkin.

Biaya untuk membeli codeword dengan panjang 0 adalah 1 - semua codeword yang memungkinkan - jika Anda ingin memiliki codeword dengan panjang 0, Anda tidak dapat memiliki codeword lain. Biaya kata sandi dengan panjang 1, misalnya, "0", adalah 1/2, karena setengah dari kemungkinan kata sandi dimulai dengan "0". Biaya codeword dengan panjang 2, misalnya "01", adalah 1/4, karena seperempat dari semua codeword yang mungkin dimulai dengan "01". Secara umum, biaya codeword berkurang secara eksponensial dengan meningkatnya panjang codeword.



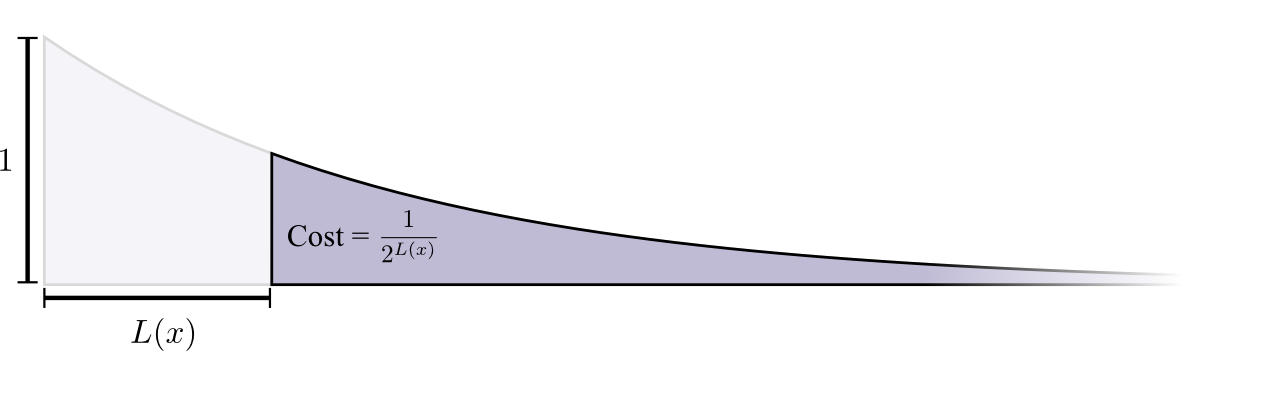
Harap dicatat bahwa jika biaya berkurang sebagai peserta pameran (dalam bentuk barang), ini adalah tinggi dan luas! ( Contoh menggunakan eksponen dengan basis 2 di mana fakta ini tidak benar, tetapi Anda dapat beralih ke eksponen alami, yang secara visual menyederhanakan bukti. )

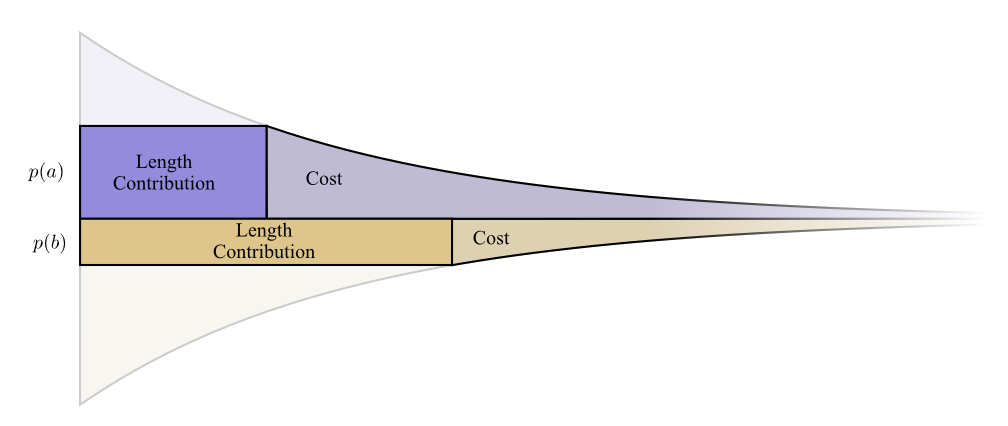
Kami membutuhkan kata sandi pendek karena kami ingin mengurangi panjang pesan rata-rata. Setiap codeword meningkatkan panjang pesan rata-rata dengan probabilitas kata tersebut kali panjangnya. Sebagai contoh, jika kita perlu mengirim kata sandi 4 bit panjang 50% dari waktu, panjang pesan rata-rata kita akan 2 bit lebih lama daripada jika kita tidak mengirim kata sandi ini. Kita bisa membayangkan ini sebagai persegi panjang.


Kedua nilai ini terkait dengan panjang kode kata. Harga yang kami bayar menentukan panjang kata kode. Panjang codeword menentukan berapa banyak yang ditambahkan ke panjang rata-rata pesan. Kita bisa membayangkan mereka bersama seperti ini.



Codeword pendek mengurangi panjang pesan rata-rata, tetapi mahal, sementara codeword panjang meningkatkan panjang pesan rata-rata, tetapi murah.



Apa cara terbaik untuk menggunakan anggaran terbatas kami? Berapa banyak yang harus kita keluarkan untuk kata sandi untuk setiap acara?

Seperti halnya seseorang ingin berinvestasi lebih banyak pada alat-alat yang dia gunakan secara teratur, kami ingin menghabiskan lebih banyak pada kata-kata kode yang umum digunakan. Ada satu cara alami untuk melakukan ini: sebarkan anggaran kami sesuai dengan seberapa sering peristiwa itu terjadi. Jadi, jika suatu peristiwa terjadi pada 50% kasus, kami menghabiskan 50% anggaran kami untuk pembelian kata kode singkat untuk itu. Tetapi jika acara hanya terjadi 1% dari waktu, kami hanya menghabiskan 1% dari anggaran kami, karena kami tidak terlalu khawatir tentang panjang kata kode.

Ini adalah hal yang cukup alami, tetapi apakah ini optimal? Ini benar, dan saya akan membuktikannya!

Bukti berikut ini jelas dan harus dipahami, tetapi perlu beberapa usaha untuk bisa keluar, dan ini jelas merupakan bagian tersulit dari esai ini. Pembaca dapat melewatinya dengan aman, menerima fakta tanpa bukti dan melanjutkan ke bagian berikutnya.

Mari kita lihat contoh spesifik di mana kita perlu memberi tahu yang mana dari dua peristiwa yang mungkin terjadi. Acara$$ terjadi$a$$$ waktu, dan acara$p(a)$$$ terjadi$b$$$ waktu. Kami mengalokasikan anggaran kami dengan cara alami yang dijelaskan di atas, belanja$p(b)$$$ anggaran kata sandi singkat kami$p(a)$$$$a$ dan $$untuk menerima kata sandi pendek$p(b)$$$$b$ .



Batas-batas biaya dan panjang berbaris indah. Apakah itu ada artinya?

Pertimbangkan apa yang terjadi pada kontribusi biaya dan panjang jika kita mengubah panjang codeword sedikit. Jika kita sedikit menambah panjang kata sandi, maka kontribusi panjang pesan akan meningkat sebanding dengan tingginya di perbatasan, dan biaya akan berkurang sebanding dengan tingginya di perbatasan.



Dengan demikian, biaya pembuatan kata sandi yang lebih pendek adalah$$$p(a)$ .Kami tidak peduli sama panjangnya setiap codeword, mereka menarik minat kami sebanding dengan seberapa sering kami menggunakannya. Dalam hal$$ adalah$a$$$$p(a)$ . Keuntungan kami dengan membuat kata sandi sedikit lebih pendek adalah proporsional $$$p(a)$.

Menariknya, kedua turunannya sama. Ini berarti bahwa anggaran awal kami memiliki fitur yang menarik: jika Anda memiliki sedikit lebih banyak uang, akan sama baiknya untuk berinvestasi dalam pengurangan setiap kata sandi. Apa yang benar-benar kita pedulikan adalah rasio manfaat / biaya - itulah yang menentukan apa yang harus kita investasikan lebih dalam. Dalam hal ini, rasionya$$ , yang sama dengan satu. Itu tidak tergantung pada nilai p (a) - selalu sama dengan kesatuan. Dan kita bisa menerapkan argumen yang sama untuk acara lain. Manfaat / biaya selalu satu, jadi masuk akal untuk berinvestasi sedikit lebih banyak di salah satu acara. Dalam hal sangat kecil, mengubah anggaran tidak masuk akal. Tapi ini bukan bukti bahwa ini adalah anggaran terbaik. Untuk membuktikan ini, kita akan melihat anggaran yang berbeda di mana kita menghabiskan sedikit lebih banyak pada satu codeword dengan mengorbankan yang lain. Kami akan habiskan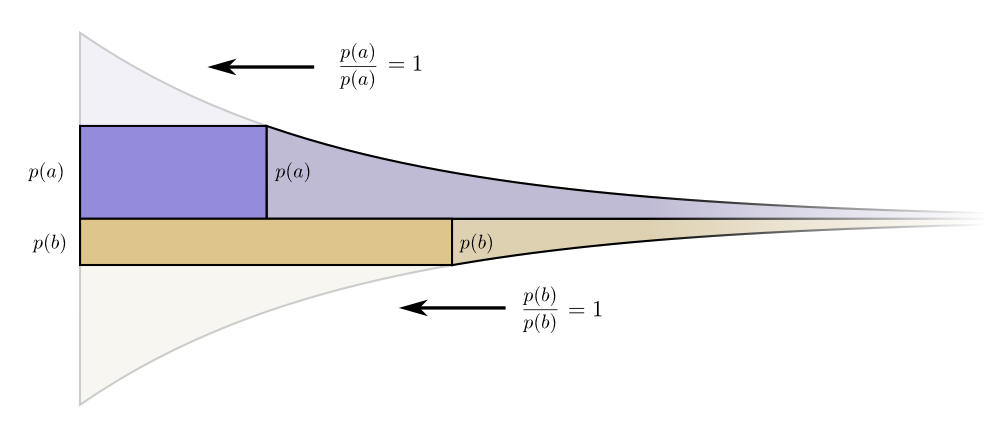$\frac{p(a)}{p(a)}$



$$kurang oleh$\epsilon$$$ dan tambahkan ini$b$$$ acara$\epsilon$$$$a$ . Itu membuat kata sandi untuk $$sedikit lebih pendek, dan kata kode untuk$a$$$ sedikit lebih lama. Sekarang harga pembelian codeword yang lebih pendek untuk$b$

$$sama$a$$$ , dan harga pembelian codeword yang lebih pendek untuk$p(a) + \epsilon$$$ sama$b$$$$p(b) − \epsilon$ .Tetapi manfaatnya sama. Ini mengarah pada fakta bahwa rasio biaya / manfaat untuk pembelian$$ kehendak$a$$$ , yang kurang dari satu. Di sisi lain, rasio biaya / manfaat dari pembelian b adalah$\frac{p (a)}{p(a) + \epsilon}$$$ , yang lebih dari satu. Harga tidak lagi seimbang.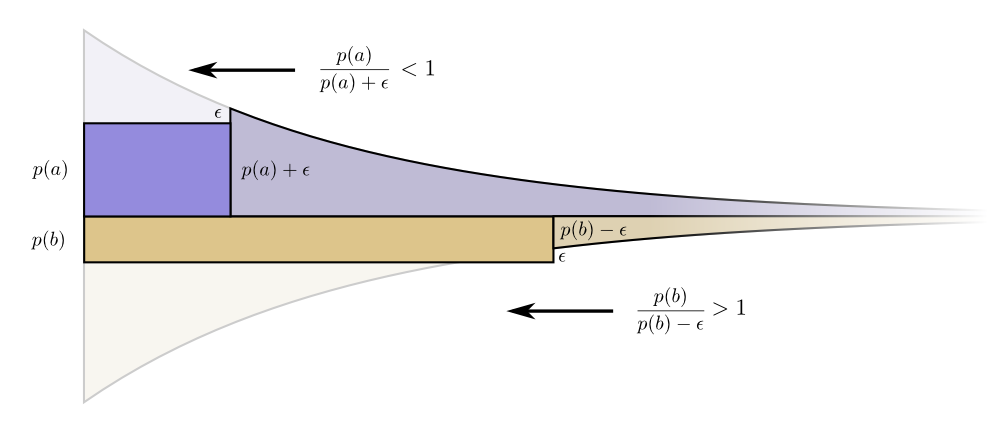$\frac{p (b)}{p(b) + \epsilon}$



$$lebih baik dari kesepakatan$b$$$$a$ . Investor berteriak: "Beli $$! Jual$b$$$ ! ”Kami melakukan ini dan kembali ke rencana anggaran semula. Semua anggaran dapat ditingkatkan dengan kembali ke rencana awal kami. Anggaran awal - berinvestasi dalam setiap codeword secara proporsional dengan seberapa sering kita menggunakannya - bukan hanya pilihan yang alami, tetapi juga optimal. (Bukti kami hanya berfungsi untuk dua codeword; dengan mudah dapat digeneralisasikan ke jumlah yang lebih besar.)$a$



(Seorang pembaca yang penuh perhatian mungkin telah memperhatikan bahwa dalam hal anggaran yang optimal, kode dapat muncul di mana kata-kata kode fraksinya panjang. Apa artinya ini? Dalam praktiknya, jika Anda ingin berkomunikasi dengan mengirim satu kata kode, Anda harus membulatkan nilainya. Tetapi bagaimana kita lihat nanti, ada perasaan nyata dalam mengirimkan kata-kata kode fraksional ketika kita mengirim banyak kata-kata pada saat yang sama!)

PS Kelanjutan dikhususkan untuk entropi, lintas-entropi, informasi bersama, bit fraksional dan hal-hal menarik lainnya.