Dasar-dasar pembelajaran mendalam pada contoh debug otomatisencoder, bagian nomor 1

Jika Anda membaca pelatihan tentang auto-encoders di situs keras.io, maka salah satu pesan pertama ada sesuatu seperti ini: dalam praktiknya, auto-encoders hampir tidak pernah digunakan, tetapi mereka sering dibicarakan dalam pelatihan dan orang-orang datang, jadi kami memutuskan untuk menulis tutorial kami sendiri tentang mereka:

Klaim utama mereka untuk ketenaran berasal dari yang ditampilkan dalam banyak kelas pembelajaran mesin pengantar tersedia online. Akibatnya, banyak pendatang baru di bidang ini benar-benar menyukai autoencoder dan tidak bisa mendapatkan cukup dari mereka. Inilah alasan mengapa tutorial ini ada!

Namun demikian, salah satu tugas praktis yang dapat diterapkan untuk diri sendiri adalah mencari anomali, dan saya secara pribadi membutuhkannya dalam kerangka proyek malam.

Di Internet, ada banyak tutorial tentang auto-encoders, untuk apa menulis satu lagi? Sejujurnya, ada beberapa alasan untuk ini:

• Ada perasaan bahwa sebenarnya tutorial itu sekitar 3 atau 4, sisanya ditulis ulang dengan kata-kata mereka sendiri;
• Hampir semuanya - di MNIST'e yang sudah lama menderita dengan gambar 28x28;
• Menurut pendapat saya yang sederhana - mereka tidak mengembangkan intuisi tentang bagaimana semua ini harus bekerja, tetapi hanya menawarkan untuk mengulang;
• Dan faktor yang paling penting - secara pribadi, ketika saya mengganti MNIST dengan dataset saya sendiri - semuanya dengan bodohnya berhenti bekerja .

Berikut ini menjelaskan jalur saya tempat memasukkan kerucut. Jika Anda mengambil salah satu dari model flat (non-convolutional) yang diusulkan dari banyak tutorial dan menyalinnya dengan bodoh, maka tidak ada, yang mengejutkan, tidak berfungsi. Tujuan artikel ini adalah untuk memahami mengapa dan, menurut saya, mendapatkan semacam pemahaman intuitif tentang bagaimana semua ini bekerja.

Saya bukan spesialis pembelajaran mesin dan menggunakan pendekatan yang saya gunakan dalam pekerjaan sehari-hari. Bagi para ilmuwan data yang berpengalaman, mungkin seluruh artikel ini akan liar, tetapi bagi pemula, bagi saya, sesuatu yang baru mungkin muncul.

Mari kita mulai. Saya memiliki dataset 4000 gambar hitam dan putih 64x64 piksel, tampilannya seperti ini:

Hanya beberapa garis pada latar belakang hitam, dan pada gambar 64x64 sekitar 2% poin terisi. Jika Anda melihat banyak gambar, maka, tentu saja, ternyata sebagian besar garis sangat mirip.

Saya tidak akan masuk ke rincian tentang bagaimana dataset dimuat, diproses, karena tujuan artikel, sekali lagi, bukan ini. Cukup tunjukkan potongan kode yang menakutkan.

# only for google colab %tensorflow_version 2.x import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import os import zipfile import datetime import tensorflow_addons as tfa BATCH_SIZE = 128 AUTOTUNE=tf.data.experimental.AUTOTUNE def load_image(fpath): img_raw = tf.io.read_file(fpath) img = tf.io.decode_png(img_raw, channels=1, dtype=tf.uint8) return tf.image.convert_image_dtype(img, dtype=tf.float32) ## for splitting test/train def is_test(x, y): return x % 4 == 0 def is_train(x, y): return not is_test(x,y) ## for image augmentation def random_flip_flop(img): return tf.image.random_flip_left_right(img) def transform_aug(shift_val): def random_transform(img): return tfa.image.translate(img,tf.random.uniform([2], -1*shift_val, shift_val)) return random_transform def prepare_for_training(ds, cache=True, shuffle_buffer_size=1000, transform=0, flip=False): if cache: if isinstance(cache, str): ds = ds.cache(cache) else: ds = ds.cache() ds = ds.shuffle(buffer_size=shuffle_buffer_size) if transform != 0: ds = ds.map(transform_aug(transform)) if flip: ds = ds.map(random_flip_flop) ds = ds.repeat() ds = ds.batch(BATCH_SIZE) ds = ds.prefetch(buffer_size=AUTOTUNE) return ds def prepare_input_output(x): return (x, x) list_ds = tf.data.Dataset.list_files("/content/planes64/*") imgs_df = list_ds.map(load_image) train = imgs_df.enumerate().filter(is_train).map(lambda x,y: y) train_ds = prepare_for_training(train, transform=10, flip=True) train_ds = train_ds.map(prepare_input_output) val = imgs_df.enumerate().filter(is_test).map(lambda x, y: y) val_ds = val.map(prepare_input_output).batch(BATCH_SIZE, drop_remainder=True) 

Di sini, misalnya, adalah model pertama yang diusulkan dengan keras.io, yang mereka kerjakan dan latih di mnist:

 # this is the size of our encoded representations encoding_dim = 32 # 32 floats -> compression of factor 24.5, assuming the input is 784 floats # this is our input placeholder input_img = Input(shape=(784,)) # "encoded" is the encoded representation of the input encoded = Dense(encoding_dim, activation='relu')(input_img) # "decoded" is the lossy reconstruction of the input decoded = Dense(784, activation='sigmoid')(encoded) 

Dalam kasus saya, model didefinisikan seperti ini:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64/10, activation='relu')) model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Ada sedikit perbedaan yang saya ratakan dan bentuk ulang langsung dalam model, dan bahwa saya "kompres" tidak 25 kali, tetapi hanya 10. Ini seharusnya tidak mempengaruhi apa pun.

Sebagai fungsi-rugi - galat kuadrat rata-rata, pengoptimal tidak mendasar, biarkan adam. Selanjutnya, kami melatih 20 era, 100 langkah per era.

Jika Anda melihat metrik - semuanya terbakar. Akurasi == 0,993. Jika Anda melihat jadwal pelatihan - semuanya sedikit lebih sedih, kami mencapai dataran tinggi di wilayah era ketiga.

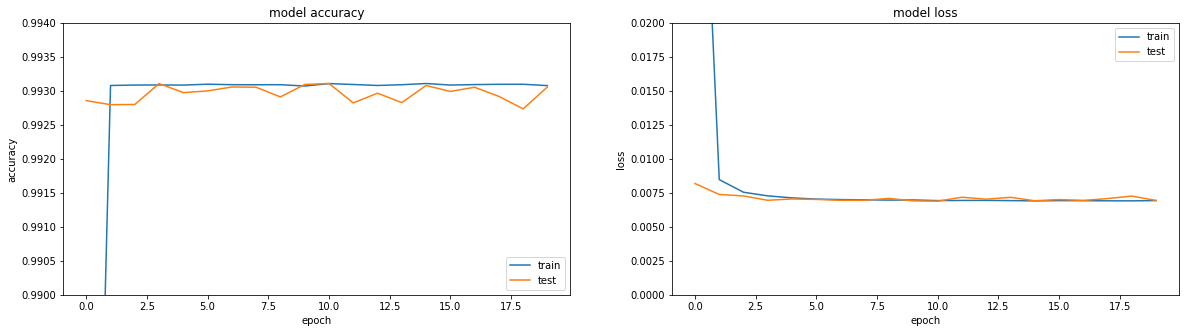
Nah, jika Anda melihat langsung pada hasil encoder, Anda mendapatkan gambar yang umumnya sedih (aslinya ada di atas, dan hasil encoding-decoding di bawah):

Secara umum, ketika Anda mencoba mencari tahu mengapa sesuatu tidak berfungsi, itu adalah pendekatan yang cukup baik untuk memecah semua fungsi menjadi blok besar dan memeriksa masing-masing secara terpisah. Jadi mari kita lakukan.

Dalam asli tutorial - data datar dipasok ke input model dan diambil pada output. Mengapa tidak memeriksa tindakan saya pada perataan dan pembentukan kembali. Berikut adalah model no-op:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Hasil:

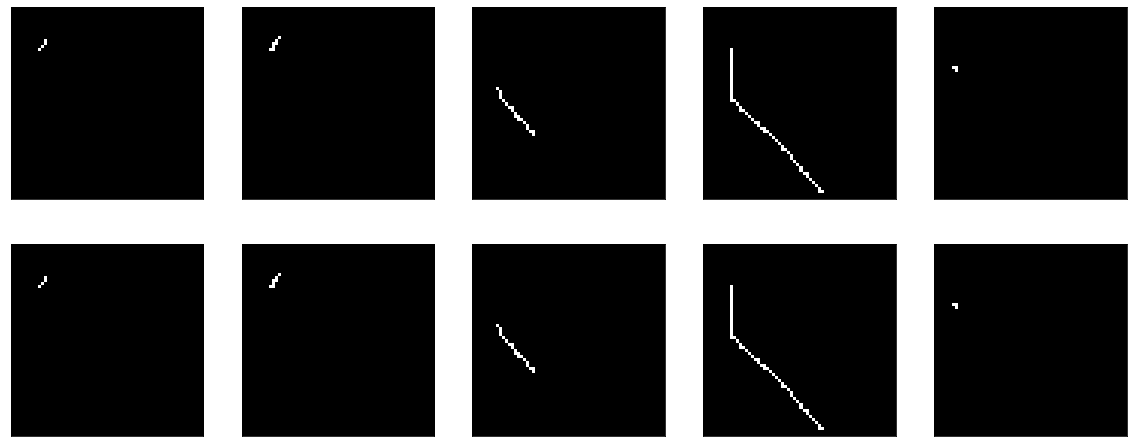
Tidak ada yang diajarkan di sini. Nah, pada saat yang sama, itu membuktikan bahwa fungsi visualisasi saya juga berfungsi.

Selanjutnya, cobalah membuat model ini bukan tanpa-op, tetapi sebodoh mungkin - cukup potong lapisan kompresi, sisakan satu lapisan ukuran input. Seperti yang mereka katakan di semua tutorial, kata mereka, sangat penting bahwa model Anda mempelajari fitur, dan bukan hanya fungsi identitas. Ya, itulah tepatnya yang akan kami coba dapatkan, mari kita sampaikan gambar yang dihasilkan ke output.

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Dia mempelajari sesuatu, akurasi == 0,995 dan lagi-lagi dia tersandung ke dataran tinggi.

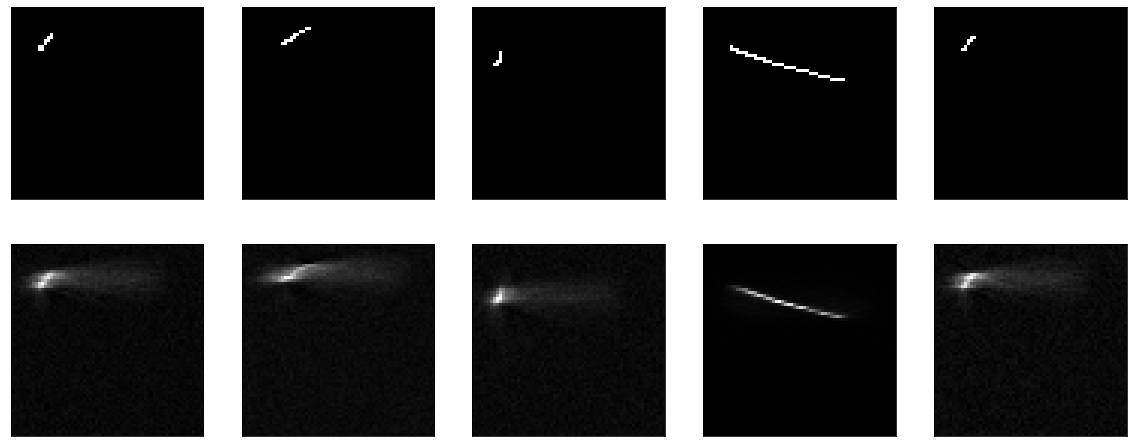
Tetapi, secara umum, jelas bahwa itu tidak bekerja dengan baik. Pokoknya - apa yang harus dipelajari di sana, melewati pintu masuk ke pintu keluar dan hanya itu.

Jika Anda membaca dokumentasi keras tentang lapisan padat, itu menjelaskan apa yang mereka lakukan: output = activation(dot(input, kernel) + bias)
Agar keluaran bertepatan dengan input, dua hal sederhana sudah cukup - bias = 0 dan kernel - matriks identitas (penting untuk tidak membiarkan matriks diisi dengan unit di sini - ini adalah hal yang sangat berbeda). Untungnya, ini dan itu bisa dilakukan dengan mudah dari dokumentasi untuk Dense sama.

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation = "sigmoid", use_bias=False, kernel_initializer = tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Karena kami segera mengatur beratnya, maka Anda tidak dapat mempelajari apa pun - segera itu bagus:

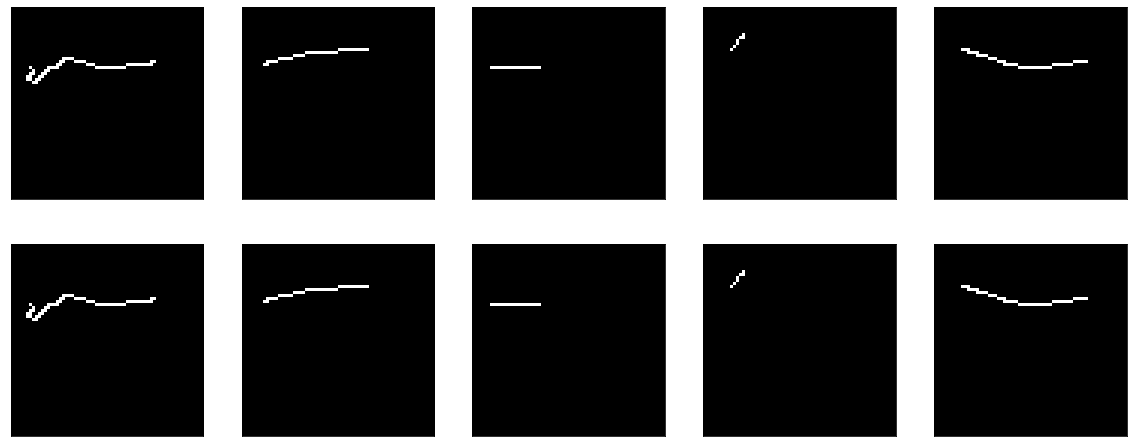
Tetapi jika Anda memulai pelatihan, maka itu dimulai, pada pandangan pertama, secara mengejutkan - model dimulai dengan akurasi == 1.0, tetapi dengan cepat jatuh.
Evaluasi hasil sebelum pelatihan: 8/Unknown - 1s 140ms/step - loss: 0.2488 - accuracy: 1.0000[0.24875330179929733, 1.0] . Pelatihan:

 Epoch 1/20 100/100 [==============================] - 6s 56ms/step - loss: 0.1589 - accuracy: 0.9990 - val_loss: 0.0944 - val_accuracy: 0.9967 Epoch 2/20 100/100 [==============================] - 5s 51ms/step - loss: 0.0836 - accuracy: 0.9964 - val_loss: 0.0624 - val_accuracy: 0.9958 Epoch 3/20 100/100 [==============================] - 5s 50ms/step - loss: 0.0633 - accuracy: 0.9961 - val_loss: 0.0470 - val_accuracy: 0.9958 Epoch 4/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0520 - accuracy: 0.9961 - val_loss: 0.0423 - val_accuracy: 0.9961 Epoch 5/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0457 - accuracy: 0.9962 - val_loss: 0.0357 - val_accuracy: 0.9962 

Ya, dan itu tidak terlalu jelas, kami sudah memiliki model yang ideal - gambar keluar 1 dalam 1, dan kerugian (berarti kuadrat kesalahan) menunjukkan hampir 0,25.

Ngomong-ngomong, ini adalah pertanyaan yang sering muncul di forum - kerugian menurun, tetapi akurasi tidak bertambah, bagaimana mungkin?
Di sini perlu diingat kembali definisi dari layer Dense: output = activation(dot(input, kernel) + bias) dan kata aktivasi yang disebutkan di dalamnya, yang berhasil saya abaikan di atas. Dengan bobot dari matriks identitas dan tanpa bias, kita mendapatkan output = activation(input) .

Sebenarnya, fungsi aktivasi dalam kode sumber kami sudah ditunjukkan, sigmoid, saya cukup bodoh menyalinnya dan hanya itu. Dan dalam tutorial disarankan untuk menggunakannya di mana-mana. Tetapi Anda harus mencari tahu.

Sebagai permulaan, Anda dapat membaca dalam dokumentasi apa yang mereka tulis tentang itu: The sigmoid activation: (1.0 / (1.0 + exp(-x))) . Itu secara pribadi tidak memberi tahu saya apa-apa, karena saya tidak phantomo sekali untuk membuat grafik seperti itu di kepala saya.
Tetapi Anda dapat membangun dengan pena:

 import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.sigmoid(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=0.5) ) plt.minorticks_on() 

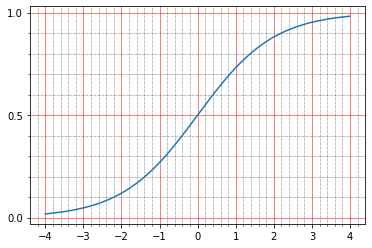
Dan di sini menjadi jelas bahwa pada nol sigmoid mengambil nilai 0,5, dan dalam unit - sekitar 0,73. Dan poin yang kami miliki adalah hitam (0,0) atau putih (1,0). Jadi ternyata kesalahan kuadrat dari fungsi identitas tetap tidak nol.

Anda bahkan dapat melihat pena, di sini ada satu baris dari gambar yang dihasilkan:

 array([0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.7310586, 0.7310586, 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 ], dtype=float32) 

Dan itu semua, pada kenyataannya, sangat keren, karena beberapa pertanyaan muncul sekaligus:

• mengapa ini tidak terlihat dalam visualisasi di atas?
• lalu mengapa akurasi == 1.0, karena gambar aslinya 0 dan 1.

Dengan visualisasi, semuanya sangat sederhana. Untuk menampilkan gambar, saya menggunakan matplotlib: plt.imshow(res_imgs[i][:, :, 0]) . Dan, seperti biasa, jika Anda pergi ke dokumentasi, semuanya akan ditulis di sana: The Normalize instance used to scale scalar data to the [0, 1] range before mapping to colors using cmap. By default, a linear scaling mapping the lowest value to 0 and the highest to 1 is used. The Normalize instance used to scale scalar data to the [0, 1] range before mapping to colors using cmap. By default, a linear scaling mapping the lowest value to 0 and the highest to 1 is used. Yaitu perpustakaan menormalkan 0,5 dan 0,73 dalam kisaran dari 0 hingga 1. Ubah kode:

 plt.imshow(res_imgs[i][:, :, 0], norm=matplotlib.colors.Normalize(0.0, 1.0)) 

Dan inilah pertanyaan dengan akurasi. Untuk mulai dengan - karena kebiasaan, kita pergi ke dokumentasi, baca untuk tf.keras.metrics.Accuracy dan di sana tampaknya mereka menulis dimengerti:

 For example, if y_true is [1, 2, 3, 4] and y_pred is [0, 2, 3, 4] then the accuracy is 3/4 or .75. 

Tetapi dalam kasus ini, keakuratan kami seharusnya 0. Saya, sebagai akibatnya, mengubur diri saya di sumber dan itu cukup jelas bagi diri saya sendiri:

  When you pass the strings 'accuracy' or 'acc', we convert this to one of `tf.keras.metrics.BinaryAccuracy`, `tf.keras.metrics.CategoricalAccuracy`, `tf.keras.metrics.SparseCategoricalAccuracy` based on the loss function used and the model output shape. We do a similar conversion for the strings 'crossentropy' and 'ce' as well. 

Selain itu, dalam dokumentasi di situs untuk beberapa alasan paragraf ini tidak ada dalam deskripsi .compile .

Berikut adalah sepotong kode dari https://github.com/tensorflow/tensorflow/blob/66c48046f169f3565d12e5fea263f6d731f9bfd2/tensorflow/python/keras/engine/compile_utils.py

 y_t_rank = len(y_t.shape.as_list()) y_p_rank = len(y_p.shape.as_list()) y_t_last_dim = y_t.shape.as_list()[-1] y_p_last_dim = y_p.shape.as_list()[-1] is_binary = y_p_last_dim == 1 is_sparse_categorical = ( y_t_rank < y_p_rank or y_t_last_dim == 1 and y_p_last_dim > 1) if metric in ['accuracy', 'acc']: if is_binary: metric_obj = metrics_mod.binary_accuracy elif is_sparse_categorical: metric_obj = metrics_mod.sparse_categorical_accuracy else: metric_obj = metrics_mod.categorical_accuracy 

y_t adalah y_true, atau output yang diharapkan, y_p adalah y_predicted, atau hasil yang diprediksi.
Kami memiliki format data: shape=(64,64,1) , sehingga ternyata akurasi dianggap sebagai binary_accuracy. Minat demi bagaimana hal itu dipertimbangkan:

 def binary_accuracy(y_true, y_pred, threshold=0.5): threshold = math_ops.cast(threshold, y_pred.dtype) y_pred = math_ops.cast(y_pred > threshold, y_pred.dtype) return K.mean(math_ops.equal(y_true, y_pred), axis=-1) 

Sangat lucu bahwa di sini kita hanya beruntung - secara default, semuanya dianggap sebagai unit yang lebih dari 0,5, dan 0,5 dan kurang - nol. Jadi akurasi keluar seratus persen untuk model identitas kita, walaupun sebenarnya jumlahnya tidak sama. Ya, jelas bahwa jika kita benar-benar ingin, maka kita dapat memperbaiki ambang batas dan mengurangi akurasi menjadi nol, misalnya, hanya saja itu tidak benar-benar diperlukan. Ini adalah metrik, itu tidak memengaruhi pelatihan, Anda hanya perlu memahami bahwa Anda dapat menghitungnya dalam ribuan cara berbeda dan mendapatkan indikator yang sama sekali berbeda. Seperti contoh, Anda dapat menarik berbagai metrik dengan pena dan mentransfer data kami kepada mereka:

 m = tf.keras.metrics.BinaryAccuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy()) 

Akan memberi kita 1.0 .

Dan disini

 m = tf.keras.metrics.Accuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy()) 

Akan memberi kami 0.0 pada data yang sama.

Ngomong-ngomong, potongan kode yang sama dapat digunakan untuk bermain dengan fungsi yang hilang dan memahami cara kerjanya. Jika Anda membaca tutorial tentang auto-encoders, maka pada dasarnya mereka menyarankan untuk menggunakan salah satu dari dua fungsi yang hilang: baik error kuadrat rata-rata atau 'binary_crossentropy'. Anda juga dapat melihatnya secara bersamaan.

Saya mengingatkan Anda bahwa untuk mse saya sudah memberikan model evaluate :

 8/Unknown - 2s 221ms/step - loss: 0.2488 - accuracy: 1.0000[0.24876083992421627, 1.0] 

Yaitu loss == 0,2488. Mari kita lihat mengapa ini terjadi. Menurut saya pribadi itu adalah yang paling sederhana dan paling dapat dipahami: perbedaan antara y_true dan y_predict dikurangi piksel demi piksel, setiap hasil dikuadratkan, kemudian hasilnya rata-rata dicari.

 tf.keras.backend.mean(tf.math.squared_difference(x_batch[0], res_imgs[0])) 

Dan pada output:

 <tf.Tensor: shape=(), dtype=float32, numpy=0.24826494> 

Di sini intuisi sangat sederhana - mayoritas piksel kosong, model menghasilkan 0,5, mereka mendapatkan 0,25 - kuadrat perbedaannya.

Dengan binary crossenttrtopy, segalanya menjadi sedikit lebih rumit, dan ada artikel lengkap tentang cara kerjanya, tetapi secara pribadi selalu lebih mudah bagi saya untuk membaca sumbernya, dan terlihat seperti ini:

  if from_logits: return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output) if not isinstance(output, (ops.EagerTensor, variables_module.Variable)): output = _backtrack_identity(output) if output.op.type == 'Sigmoid': # When sigmoid activation function is used for output operation, we # use logits from the sigmoid function directly to compute loss in order # to prevent collapsing zero when training. assert len(output.op.inputs) == 1 output = output.op.inputs[0] return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output) # Compute cross entropy from probabilities. bce = target * math_ops.log(output + epsilon()) bce += (1 - target) * math_ops.log(1 - output + epsilon()) return -bce 

Sejujurnya, saya memutar otak atas beberapa baris kode ini untuk waktu yang sangat lama. Pertama, segera jelas bahwa dua implementasi dapat bekerja: baik sigmoid_cross_entropy_with_logits akan dipanggil, atau sepasang baris terakhir akan berfungsi. Perbedaannya adalah bahwa sigmoid_cross_entropy_with_logits berfungsi dengan logit (sesuai namanya, doh), dan kode utama berfungsi dengan probabilitas.

Siapa yang log? Jika Anda membaca sejuta artikel berbeda tentang topik ini, maka mereka akan menyebutkan definisi, rumus, dan hal lain dalam matematika. Dalam praktiknya, semuanya tampak sangat sederhana (koreksi saya jika saya salah). Output mentah dari prediksi adalah log. Nah, atau peluang-log, peluang logaritmik yang diukur dalam log istic un -nya - beo logistik.

 ln(1/2) == -0.69 ln(2/1) == 0.69 ln(1/100) == -4.6 ln(100/1) == 4.6 

Dalam kasus tensorflow, ini agak arbitrer, karena, secara tegas, output dari layer secara matematis bukan log-odds, tetapi sudah diterima. Jika nilai mentahnya dari -∞ hingga + ∞ - lalu log. Kemudian mereka dapat dikonversi menjadi probabilitas. Ada dua opsi untuk ini: softmax dan kasing khusus, sigmoid. Softmax - Mengambil vektor log dan mengubahnya menjadi vektor probabilitas, dan meskipun demikian jumlah probabilitas semua peristiwa di dalamnya ternyata 1. Sigmoid (dalam kasus tf) juga mengambil vektor log, tetapi mengonversi masing-masing menjadi probabilitas secara terpisah, secara terpisah. dari yang lain.

 # 1+ln(0.5) == 0.30685281944 tf.math.softmax(tf.constant([0.30685281944, 1.0, 0.30685281944])) ## <tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.25, 0.5 , 0.25], dtype=float32)> tf.math.sigmoid(tf.constant([0.30685281944, 1.0, 0.30685281944])) ## <tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.57611686, 0.7310586 , 0.57611686], dtype=float32)> 

Anda bisa melihatnya dengan cara ini. Ada tugas klasifikasi multi-label, ada tugas klasifikasi multi-kelas. Multiclass - ini adalah jika Anda perlu menentukan apel dalam gambar atau jeruk, dan mungkin bahkan nanas. Dan multilabel adalah ketika ada vas buah di gambar dan Anda perlu mengatakan bahwa ada apel dan jeruk di atasnya, tetapi tidak ada nanas. Jika kita ingin multiclass - kita perlu softmax, jika kita ingin multilabel - kita perlu sigmoid.
Di sini kita memiliki kasus multilabel - perlu untuk setiap pixel individu (kelas) untuk mengatakan apakah itu diinstal.

Kembali ke tensorflow dan mengapa dalam crossentropy biner (paling tidak dalam fungsi crossentropy lainnya hampir sama) ada dua cabang global. Crossentropy selalu bekerja dengan probabilitas, kami akan membicarakannya nanti. Kemudian hanya ada dua cara: probabilitas sudah masuk input, atau log datang ke input - dan kemudian sigmoid diterapkan pertama kali untuk mendapatkan probabilitas. Kebetulan menerapkan sigmoid dan menghitung crossentropy ternyata lebih baik daripada hanya menghitung crossentropy dari probabilitas (output matematika dari alasannya adalah dalam sumber fungsi sigmoid_cross_entropy_with_logits , plus bagi yang penasaran Anda dapat google 'stabilitas numerik lintas entropi'), sehingga bahkan para pengembang lambat dapat merekomendasikan untuk tidak melewatkan probabilitas untuk melewati probabilitas. input fungsi crossentropy, dan memberikan kembali log mentah. Nah, tepat di kode, fungsi kerugian diperiksa jika lapisan terakhir adalah sigmoid, maka mereka akan memotongnya dan mengambil input aktivasi, bukan outputnya, untuk menghitung, mengirim semuanya untuk dipertimbangkan dalam sigmoid_cross_entropy_with_logits .

Oke, bereskan, sekarang binary_crossentropy. Ada dua penjelasan "intuitif" populer yang mengukur cross-entropy.

Lebih formal: bayangkan bahwa ada model tertentu yang untuk n kelas tahu probabilitas kemunculannya (y ₀ , y ₁ , ..., y _n ). Dan sekarang dalam kehidupan, masing-masing kelas ini telah muncul k _n kali (k ₁ , k ₁ , ..., k _n ). Probabilitas peristiwa semacam itu adalah produk dari probabilitas untuk setiap kelas individu - (y ₁ ^ k ₁ ) (y ₂ ^ k ₂ ) ... (y _n ^ k _n ). Pada prinsipnya - ini sudah merupakan definisi normal dari cross-entropy - probabilitas satu dataset dinyatakan dalam probabilitas dari dataset lain. Masalah dengan definisi ini adalah bahwa itu akan berubah dari 0 ke 1 dan akan sering sangat kecil, tidak nyaman untuk membandingkan nilai-nilai tersebut.
Jika kita mengambil logaritma dari ini, maka k ₁ log (y ₁ ) + k ₂ log (y ₂ ) akan keluar dan seterusnya. Kisaran nilai menjadi dari -∞ hingga 0. Lipat gandakan semua ini dengan -1 / n - dan rentang dari 0 hingga + ∞ keluar, apalagi, karena itu dinyatakan sebagai jumlah nilai untuk setiap kelas, perubahan di setiap kelas tercermin dalam nilai keseluruhan dengan cara yang sangat dapat diprediksi.

Lebih sederhana: cross-entropy menunjukkan berapa banyak bit tambahan yang diperlukan untuk mengekspresikan sampel dalam hal model asli. Jika kita ada di sana untuk membuat logaritma dengan basis 2, maka kita akan langsung bit. Kami menggunakan logaritma alami di mana-mana, sehingga menunjukkan jumlah nat ( https://en.wikipedia.org/wiki/Nat_(unit )), bukan bit.

Binary cross-entropy, pada gilirannya, adalah kasus khusus dari cross-entropy biasa, ketika jumlah kelas adalah dua. Kemudian kita memiliki pengetahuan yang cukup tentang probabilitas kemunculan satu kelas - y ₁ , dan probabilitas yang kedua adalah (1-y ₁ ).

Tapi, bagi saya, agak membuat saya tergelincir. Biarkan saya mengingatkan Anda, terakhir kali kami mencoba membangun sebuah auto-encoder identitas, dia menunjukkan kepada kita sebuah gambar yang indah, dan bahkan akurasi 1,0, tetapi ternyata angkanya ternyata mengerikan. Demi percobaan, Anda dapat melakukan beberapa tes lagi:
1) aktivasi dapat dihapus sama sekali, akan ada identitas bersih
2) Anda dapat mencoba fungsi aktivasi lainnya, misalnya relu yang sama

Tanpa aktivasi:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Kami mendapatkan model identitas yang sempurna:

 model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True)) # 8/Unknown - 1s 173ms/step - loss: 0.0000e+00 - accuracy: 1.0000[0.0, 1.0] 

Ngomong-ngomong, pelatihan tidak akan mengarah pada apa pun, karena kerugian == 0,0.

Sekarang dengan relu. Grafiknya terlihat seperti ini:

 import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.relu(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=1) ) plt.minorticks_on() 

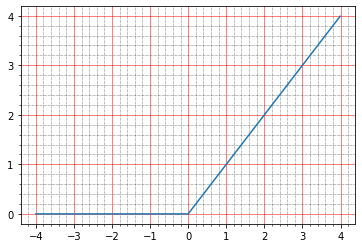
Di bawah nol - nol, di atas - y = x, yaitu dalam teori, kita harus mendapatkan efek yang sama dengan tidak adanya aktivasi - model yang ideal.

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["accuracy"]) model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True)) # 8/Unknown - 1s 158ms/step - loss: 0.0000e+00 - accuracy: 1.0000[0.0, 1.0] 

Oke, kami menemukan model identitas, bahkan dengan beberapa bagian dari teori itu menjadi lebih jelas. Sekarang mari kita coba latih model yang sama sehingga menjadi identitas.

Untuk bersenang-senang, saya akan melakukan percobaan ini pada tiga fungsi aktivasi. Untuk mulai dengan - relu, karena ia menunjukkan dirinya jauh lebih awal (semuanya seperti sebelumnya, tetapi kernel_initializer dihapus, jadi secara default akan glorot_uniform ):

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Ia belajar dengan luar biasa:

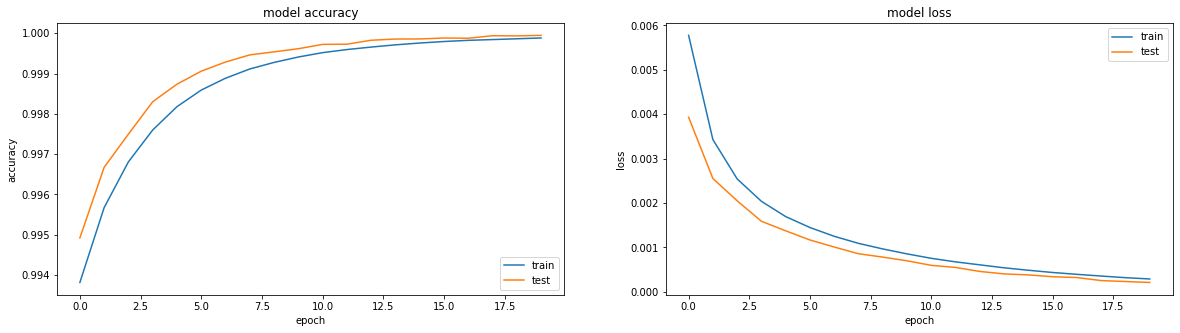
Hasilnya cukup bagus, akurasi: 0,9999, loss (mse): 2e-04 setelah 20 era dan Anda bisa berlatih lebih lanjut.

Selanjutnya, coba dengan sigmoid:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Saya sudah mengajarkan sesuatu yang serupa sebelumnya, dengan satu-satunya perbedaan adalah bahwa bias dinonaktifkan di sini. Dia belajar dengan tenang, pergi di dataran tinggi di wilayah era ke-50, akurasi: 0,9970, kerugian: 0,01 setelah 60 era.

Hasilnya lagi tidak mengesankan:

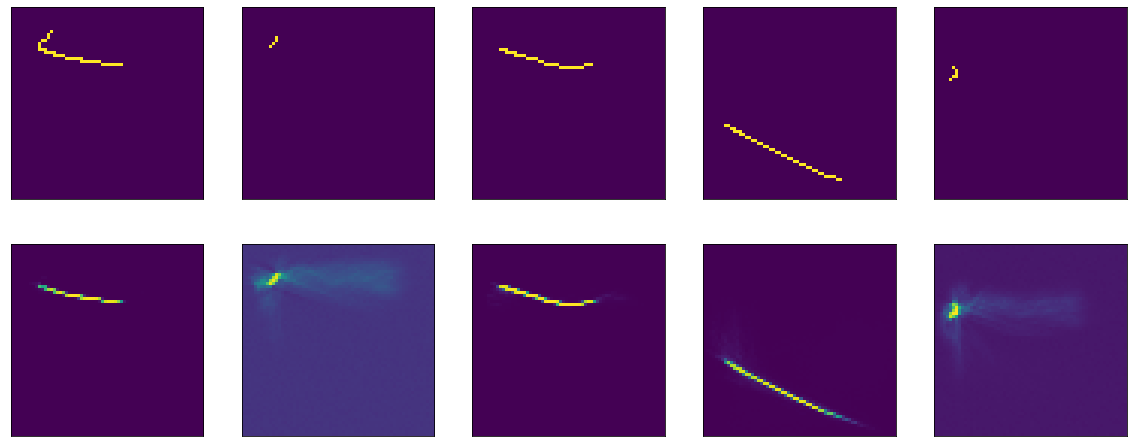
Nah, periksa juga tanh:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='tanh', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Hasilnya sebanding dengan relu - akurasi: 0,9999, loss: 6e-04 setelah 20 era, dan Anda dapat melatih lebih lanjut:

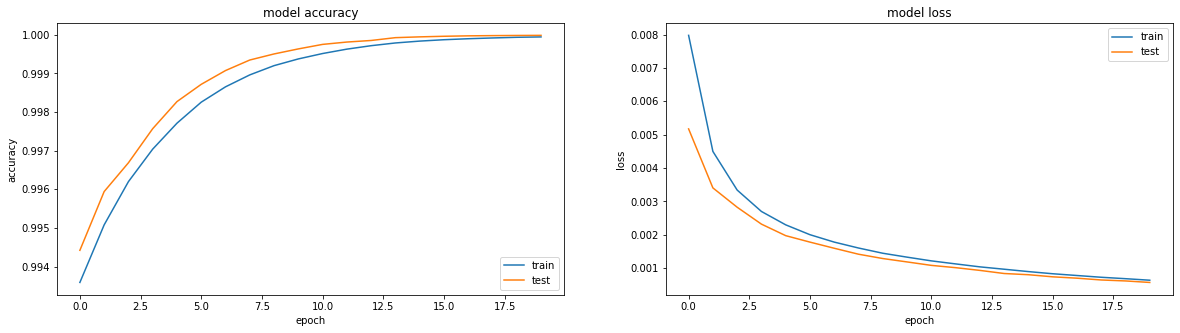
Bahkan, saya tersiksa oleh pertanyaan apakah sesuatu dapat dilakukan untuk membuat sigmoid menunjukkan hasil yang sebanding. Khusus karena minat olahraga.

Misalnya, Anda dapat mencoba menambahkan BatchNormalisasi:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.BatchNormalization()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Dan kemudian semacam sihir terjadi. Di era ke-13, akurasi: 1.0. Dan hasil yang berapi-api:

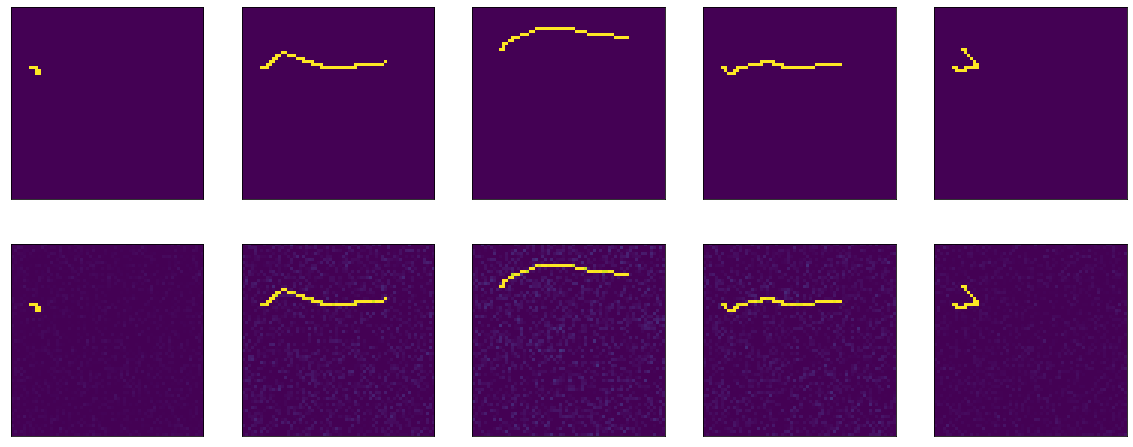
III ... di gantungan tebing ini saya akan menyelesaikan bagian pertama, karena teks terlalu dofig, dan tidak jelas apakah seseorang membutuhkannya atau tidak. Pada bagian kedua, saya akan memahami apa yang terjadi dengan sihir, bereksperimen dengan pengoptimal yang berbeda, mencoba membangun penyandi-dekoder yang jujur, membenturkan kepala ke atas meja. Saya harap seseorang tertarik dan membantu.