SVM Penjelasan dari awal dan implementasi dalam python. Analisis terperinci tentang metode vektor dukungan

Halo semua yang memilih jalur ML-Samurai!

Pendahuluan:

Pada artikel ini, kami mempertimbangkan metode mesin dukungan vektor ( Eng. SVM, Support Vector Machine ) untuk masalah klasifikasi. Ide utama dari algoritma akan disajikan, output pengaturan bobotnya dan implementasi DIY sederhana akan dianalisis. Pada contoh dataset $$$Iris$pengoperasian algoritma tertulis dengan data yang dapat dipisahkan / tidak terpisahkan secara linear dalam ruang akan ditunjukkan $$$R ^ 2$dan visualisasi pelatihan / prognosis. Selain itu, pro dan kontra dari algoritma, modifikasinya akan diumumkan.

Gambar 1. Foto sumber terbuka bunga iris

Masalah yang harus dipecahkan:

Kami akan memecahkan masalah klasifikasi biner (ketika hanya ada dua kelas). Pertama, algoritma melatih objek dari set pelatihan, yang label kelasnya diketahui sebelumnya. Selanjutnya, algoritma yang sudah terlatih memprediksi label kelas untuk setiap objek dari sampel ditangguhkan / uji. Label kelas dapat mengambil nilai $$$Y = \ {- 1, +1 \}$ . Objek - vektor dengan tanda N $$$x = (x_1, x_2, ..., x_n)$di luar angkasa $$$R ^ n$. Saat belajar, algoritma harus membangun suatu fungsi $$$F (x) = y$yang membutuhkan argumen $$$x$- Objek dari luar angkasa $$$R ^ n$dan memberi label kelas $$$y$.

Kata-kata umum tentang algoritma:

Tugas klasifikasi berkaitan dengan mengajar dengan seorang guru. SVM adalah algoritma pembelajaran dengan seorang guru. Secara visual, banyak algoritma pembelajaran mesin dapat ditemukan di artikel top-notch ini (lihat bagian "Peta dunia pembelajaran mesin"). Harus ditambahkan bahwa SVM juga dapat digunakan untuk masalah regresi, tetapi classifier SVM akan dianalisis dalam artikel ini.

Tujuan utama SVM sebagai classifier adalah untuk menemukan persamaan hyperplane pemisah
$$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 = 0$di luar angkasa $$$R ^ n$, yang akan membagi dua kelas dalam beberapa cara yang optimal. Pandangan umum dari transformasi $$$F$fasilitas $$$x$ke label kelas $$$Y$: $$$F (x) = tanda (w ^ Tx-b)$. Kami akan ingat bahwa kami telah ditunjuk $$$w = (w_1, w_2, ..., w_n), b = -w_0$. Setelah mengatur bobot algoritma $$$w$dan $$$b$(pelatihan), semua benda yang jatuh di satu sisi hyperplane yang dibangun akan diprediksi sebagai kelas pertama, dan benda yang jatuh di sisi lain - kelas kedua.

Fungsi dalam $$$sign ()$ada kombinasi linear fitur objek dengan bobot algoritma, itulah sebabnya SVM mengacu pada algoritma linier. Hyperplane pemisah dapat dibangun dengan cara yang berbeda, tetapi dalam bobot SVM $$$w$dan $$$b$dikonfigurasikan sehingga objek kelas terletak sejauh mungkin dari hyperplane pemisah. Dengan kata lain, algoritma memaksimalkan celah ( margin bahasa Inggris ) antara hyperplane dan objek kelas yang paling dekat dengannya. Objek semacam itu disebut vektor penunjang (lihat Gambar 2). Karena itulah nama algoritma.

Gambar 2. SVM (dasar gambar dari sini )

Output terperinci dari aturan penyesuaian skala SVM:

Untuk menjaga hyperplane pemisah sejauh mungkin dari titik sampel, lebar strip harus maksimum. Vektor $$$w$Apakah vektor mengarahkan hyperplane pemisah. Selanjutnya, kami menyatakan produk skalar dari dua vektor sebagai $$$\ langle a, b \ rangle$atau $$$a ^ Tb$. Mari kita temukan proyeksi vektor yang ujungnya akan menjadi vektor dukungan dari kelas yang berbeda pada vektor arah hyperplane. Proyeksi ini akan menunjukkan lebar strip pemisah (lihat Gambar 3):

Gambar 3. Output dari aturan untuk mengatur skala (dasar gambar dari sini )

Margin objek x dari batas kelas adalah nilai $$$M = y (w ^ Tx-b)$. Algoritma membuat kesalahan pada objek jika dan hanya jika indentasi $$$M$negatif (ketika $$$y$dan $$$(w ^ Tx-b)$karakter yang berbeda). Jika $$$M ∈ (0, 1)$, lalu objek jatuh di dalam strip pemisah. Jika $$$M> 1$, maka objek x diklasifikasikan dengan benar, dan terletak agak jauh dari strip pembagi. Kami menuliskan koneksi ini:

Sistem yang dihasilkan adalah pengaturan SVM default dengan SVM hard-margin , ketika tidak ada objek yang diizinkan untuk memasuki band separasi. Ini diselesaikan secara analitis melalui teorema Kuhn-Tucker. Masalah yang dihasilkan setara dengan masalah ganda dalam menemukan titik sadel fungsi Lagrange.

$$$$ menampilkan $$ \ kiri \ {\ mulai {array} {ll} (w ^ Tw) / 2 \ min kanan & & textrm {} \\ y (w ^ Tx-b) \ geqslant 1 & \ textrm {} \ end {array} \ benar. $$ tampilan $$

Semua ini bagus selama kelas kita terpisah secara linear. Agar algoritme dapat bekerja dengan data yang tidak dapat dipisahkan secara linear, mari kita ubah sistem kita sedikit. Biarkan algoritma membuat kesalahan pada objek pelatihan, tetapi pada saat yang sama cobalah untuk menjaga kesalahan lebih sedikit. Kami memperkenalkan serangkaian variabel tambahan $$$\ xi _i> 0$mengkarakterisasi besarnya kesalahan pada setiap objek $$$x_i$. Kami memperkenalkan penalti untuk kesalahan total ke dalam fungsional yang diperkecil:

$$$$ menampilkan $$ \ kiri \ {\ mulai {array} {ll} (w ^ Tw) / 2 + \ alpha \ jumlah \ xi _i \ min kanan-kanan & \ textrm {} \\ y (w ^ Tx_i-b) \ geqslant 1 - \ xi _i & \ textrm {} \\ \ xi _i \ geqslant0 & \ textrm {} \ end {array} \ benar. $$ tampilan $$

Kami akan mempertimbangkan jumlah kesalahan algoritma (ketika M <0). Sebut saja Penalti . Maka penalti untuk semua objek akan sama dengan jumlah denda untuk setiap objek $$$x_i$dimana $$$[M_i <0]$- fungsi threshold (lihat Gambar 4):

$$$$ menampilkan $$ [M_i <0] = \ kiri \ {\ mulai {array} {ll} 1 & \ textrm {jika} M_i <0 \\ 0 & \ textrm {jika} M_i \ geqslant 0 \ end {array} \ benar. $$ tampilan $$

Selanjutnya, kami membuat penalti peka terhadap besarnya kesalahan dan pada saat yang sama memperkenalkan penalti untuk mendekati objek ke batas kelas:

Saat menambahkan ekspresi penalti, istilah tersebut $$$\ alpha (w ^ Tw) / 2$kita mendapatkan fungsi kerugian SVM klasik dengan soft gap ( soft-margin SVM ) untuk satu objek:

$$$Q$- Fungsi kerugian, juga merupakan fungsi kerugian. Itulah yang akan kami meminimalkan dengan bantuan gradient descent dalam implementasi tangan. Kami mendapatkan aturan untuk mengubah bobot, di mana $$$\ eta$- langkah turun:

$$$$ menampilkan $$ \ bigtriangledown Q = \ kiri \ {\ mulai {array} {ll} \ alpha w-yx & \ textrm {jika} yw ^ Tx <1 \\ \ alpha w & \ textrm {jika} yw ^ Tx \ geqslant 1 \ end {array} \ benar. $$ tampilan $$

Kemungkinan pertanyaan saat wawancara (berdasarkan peristiwa nyata):

Setelah pertanyaan umum tentang SVM: Mengapa Hinge_loss memaksimalkan izin? - pertama, ingatlah bahwa hyperplane mengubah posisinya ketika bobot berubah $$$w$dan $$$b$. Bobot algoritma mulai berubah ketika gradien dari fungsi kerugian tidak sama dengan nol (mereka biasanya mengatakan: "aliran gradien"). Oleh karena itu, kami secara khusus memilih fungsi kerugian seperti itu, di mana gradien mulai mengalir pada waktu yang tepat. $$$Kerugian engsel$terlihat seperti ini: $$$H = maks (0,1-y (w ^ Tx))$. Ingat izin itu $$$m = y (w ^ Tx)$. Saat jeda $$$m$cukup besar ( $$$1$atau lebih) ekspresi $$$(1-m)$menjadi kurang dari nol dan $$$H = 0$(Oleh karena itu, gradien tidak mengalir dan bobot algoritma tidak berubah dengan cara apa pun). Jika celah m cukup kecil (misalnya, ketika suatu objek jatuh ke dalam pita pemisahan dan / atau negatif (jika perkiraan klasifikasi salah), maka Hinge_loss menjadi positif ( $$$H> 0$), gradien mulai mengalir dan bobot algoritma berubah. Meringkas: gradien mengalir dalam dua kasus: ketika objek sampel jatuh di dalam pita pemisahan dan ketika objek diklasifikasikan secara tidak benar.

Untuk memeriksa level bahasa asing, pertanyaan serupa dimungkinkan: Apa persamaan dan perbedaan antara LogisticRegression dan SVM? - pertama, kita akan berbicara tentang kesamaan: kedua algoritma adalah algoritma klasifikasi linier dalam pembelajaran yang diawasi. Beberapa kesamaan ada dalam argumen fungsi kerugian: $$$log (1 + exp (-y (w ^ Tx)))$untuk logreg dan $$$maks (0,1-y (w ^ Tx))$untuk SVM (lihat gambar 4). Kedua algoritma tersebut dapat kita konfigurasikan menggunakan gradient descent. Selanjutnya mari kita bicara tentang perbedaan: SVM mengembalikan label kelas objek tidak seperti LogReg, yang mengembalikan probabilitas keanggotaan kelas. SVM tidak dapat bekerja dengan label kelas $$$\ {0,1 \}$ (tanpa mengganti nama kelas) tidak seperti LogReg (LogReg kehilangan alasan untuk $$$\ {0,1 \}$ : $$$-ylog (p) - (1-y) log (1-p)$dimana $$$y$- label kelas nyata, $$$p$- Pengembalian algoritma, probabilitas objek yang dimiliki $$$x$ke kelas $$$\ {1 \}$ ) Lebih dari itu, kita dapat memecahkan masalah SVM hard-margin tanpa gradient descent. Tugas mencari vektor dukungan direduksi menjadi titik sadel pencarian di fungsi Lagrange - tugas ini hanya merujuk pada pemrograman kuadratik.

import numpy as np import matplotlib.pyplot as plt %matplotlib inline xx = np.linspace(-4,3,100000) plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0') plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)') plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)') plt.title('Loss = F(Margin)') plt.grid() plt.legend(prop={'size': 14}); 

Gambar 4. Fungsi kerugian

Implementasi sederhana SVM soft-margin klasik:

Perhatian! Anda akan menemukan tautan ke kode lengkap di akhir artikel. Di bawah ini adalah blok kode yang diambil di luar konteks. Beberapa blok hanya dapat dimulai setelah mengerjakan blok sebelumnya. Di bawah banyak blok, gambar akan ditempatkan yang menunjukkan bagaimana kode yang ditempatkan di atasnya bekerja.

 import numpy as np import warnings warnings.filterwarnings('ignore') import matplotlib.pyplot as plt import matplotlib.lines as mlines plt.rcParams['figure.figsize'] = (8,6) %matplotlib inline from sklearn.datasets import load_iris from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split def newline(p1, p2, color=None): #    #function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib ax = plt.gca() xmin, xmax = ax.get_xbound() if(p2[0] == p1[0]): xmin = xmax = p1[0] ymin, ymax = ax.get_ybound() else: ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0]) ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0]) l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color) ax.add_line(l) return l 

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended class CustomSVM(object): __class__ = "CustomSVM" __doc__ = """ This is an implementation of the SVM classification algorithm Note that it works only for binary classification ############################################################# ###################### PARAMETERS ###################### ############################################################# etha: float(default - 0.01) Learning rate, gradient step alpha: float, (default - 0.1) Regularization parameter in 0.5*alpha*||w||^2 epochs: int, (default - 200) Number of epochs of training ############################################################# ############################################################# ############################################################# """ def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) def predict(self, X:np.array) -> np.array: y_pred = [] X_extended = add_bias_feature(X) for i in range(len(X_extended)): y_pred.append(np.sign(np.dot(self._w,X_extended[i]))) return np.array(y_pred) def hinge_loss(self, x, y): return max(0,1 - y*np.dot(x, self._w)) def soft_margin_loss(self, x, y): return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w) 

Kami mempertimbangkan secara rinci pengoperasian setiap blok garis:

1) membuat fungsi add_bias_feature (a) , yang secara otomatis memperluas vektor objek, menambahkan angka 1 ke akhir setiap vektor.Ini diperlukan untuk "lupa" tentang istilah bebas b. Ekspresi $$$w ^ Tx-b$setara dengan ungkapan $$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 * 1$. Kami mengasumsikan bahwa unit adalah komponen terakhir dari vektor untuk semua vektor x, dan $$$w_0 = -b$. Sekarang atur bobotnya $$$w$dan $$$w_0$Kami akan memproduksi pada saat yang sama.

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended 

2) maka kita akan menggambarkan classifier itu sendiri. Ini memiliki fungsi inisialisasi init () , fit pembelajaran () , memprediksi memprediksi () , menemukan hilangnya fungsi hinge_loss () dan menemukan total kehilangan fungsi dari algoritma klasik dengan soft_margin_loss () .

3) saat inisialisasi, 3 hiperparameter diperkenalkan: _etha - langkah gradient descent ( $$$\ eta$), _alpha - koefisien kecepatan penurunan berat badan proporsional (sebelum istilah kuadratik dalam fungsi penurunan) $$$\ alpha$), _epochs - jumlah era pelatihan.

  def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None 

4) selama pelatihan untuk setiap era sampel pelatihan (X_train, Y_train) kita akan mengambil satu elemen dari sampel, menghitung jarak antara elemen ini dan posisi hyperplane pada waktu tertentu. Selanjutnya, tergantung pada ukuran celah ini, kami akan mengubah bobot algoritma menggunakan gradien fungsi kerugian $$$Q$. Pada saat yang sama, kami akan menghitung nilai fungsi ini untuk setiap zaman dan berapa kali kami mengubah bobot per zaman. Sebelum memulai pelatihan, kami akan memastikan bahwa tidak lebih dari dua label kelas yang berbeda telah benar-benar masuk ke dalam fungsi pembelajaran. Sebelum mengatur keseimbangan, ini diinisialisasi dengan menggunakan distribusi normal.

  def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) 

Memeriksa pengoperasian algoritma tertulis:

Periksa apakah algoritma tertulis kami berfungsi pada beberapa jenis kumpulan data mainan. Ambil dataset Iris. Kami akan menyiapkan data. Nyatakan kelas 1 dan 2 sebagai $$$+ 1$, dan kelas 0 sebagai $$$-1$. Dengan menggunakan algoritma PCA (penjelasan dan aplikasi di sini ), kami secara optimal mengurangi ruang dari 4 atribut menjadi 2 dengan kehilangan data minimal (akan lebih mudah bagi kami untuk mengamati pelatihan dan hasilnya). Selanjutnya, kami akan membagi menjadi sampel pelatihan (kereta) dan yang tertunda (validasi). Kami akan melatih sampel pelatihan, memprediksi dan memeriksa yang ditangguhkan. Kami memilih faktor pembelajaran sehingga fungsi kerugian turun. Selama pelatihan, kita akan melihat fungsi kerugian dari pelatihan dan pengambilan sampel yang tertunda.

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

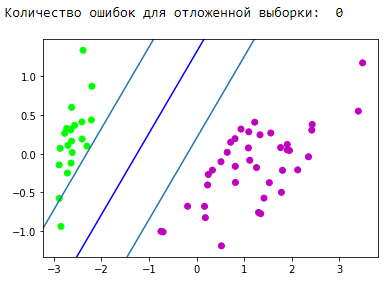
Hebat! Algoritma kami menangani data yang dapat dipisahkan secara linear. Sekarang buat kelas menjadi terpisah 0 dan 1 dari kelas 2:

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors[:150]) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

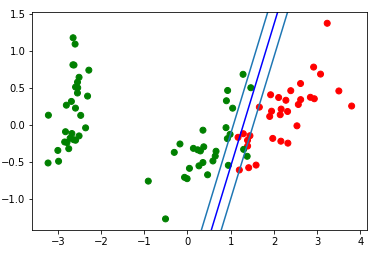
Mari kita lihat gif, yang akan menunjukkan bagaimana garis pemisah mengubah posisinya selama pelatihan (total 500 frame mengubah bobot. 300 pertama berturut-turut. 200 lembar berikutnya untuk setiap frame 130):

 import matplotlib.animation as animation from matplotlib.animation import PillowWriter def one_image(w, X, Y): axes = plt.gca() axes.set_xlim([-4,4]) axes.set_ylim([-1.5,1.5]) d1 = {-1:'green', 1:'red'} im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y]) im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue') # im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1 # im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 return im fig = plt.figure() ims = [] for i in range(500): if i<=300: k = i else: k = (i-298)*130 im = one_image(svm.history_w[k], X_train, Y_train) ims.append([im]) ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True, repeat_delay=500) writer = PillowWriter(fps=20) ani.save("my_demo.gif", writer='imagemagick') 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

Meluruskan ruang

Penting untuk dipahami bahwa dalam masalah nyata tidak akan ada kasus sederhana dengan data yang dapat dipisahkan secara linear. Untuk bekerja dengan data tersebut, ide pindah ke ruang lain diusulkan, di mana data akan terpisah secara linear. Ruang seperti ini disebut perbaikan. Ruang perbaikan dan kernel tidak akan terpengaruh dalam artikel ini. Anda dapat menemukan teori matematika paling lengkap di 14,15,16 sinopsis E. Sokolov dan dalam kuliah K.V. Vorontsov .

Menggunakan SVM dari sklearn:

Faktanya, hampir semua algoritma pembelajaran mesin klasik ditulis untuk Anda. Mari kita beri contoh kode, kita akan mengambil algoritma dari pustaka sklearn .

 from sklearn import svm from sklearn.metrics import recall_score C = 1.0 # = self._alpha in our algorithm model1 = svm.SVC(kernel='linear', C=C) #model1 = svm.LinearSVC(C=C, max_iter=10000) #model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C) #model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C) model1.fit(X_train, Y_train) y_predict = model1.predict(X_test) print(recall_score(Y_test, y_predict, average=None)) 

Pro dan kontra dari SVM klasik:

Pro:

1. bekerja dengan baik dengan ruang fitur besar;
2. bekerja dengan baik dengan data kecil;
3. Jadi algoritma menemukan memaksimalkan band pembagi, yang, seperti airbag, dapat mengurangi jumlah kesalahan klasifikasi;
4. karena algoritma mengurangi untuk memecahkan masalah pemrograman kuadratik dalam domain cembung, masalah seperti itu selalu memiliki solusi yang unik (memisahkan hyperplane dengan hyperparameter algoritma tertentu selalu sama).

Cons:

1. waktu pelatihan yang panjang (untuk set data besar);
2. ketidakstabilan kebisingan: pencilan dalam data pelatihan menjadi objek pengganggu referensi dan secara langsung memengaruhi konstruksi hyperplane pemisah;
3. metode umum untuk membangun kernel dan ruang perbaikan yang paling cocok untuk masalah spesifik dalam kasus ketidakterpisahan linear kelas tidak dijelaskan. Memilih transformasi data yang bermanfaat adalah seni.

Aplikasi SVM:

Pilihan satu atau yang lain algoritma pembelajaran mesin secara langsung tergantung pada informasi yang diperoleh selama penambangan data. Namun secara umum, tugas-tugas berikut dapat dibedakan:

• tugas dengan kumpulan data kecil;
• tugas klasifikasi teks. SVM memberikan baseline yang baik ([preprocessing] + [TF-iDF] + [SVM]), akurasi perkiraan yang dihasilkan berada pada level beberapa jaringan saraf convolutional / berulang (saya sarankan mencoba metode ini sendiri untuk mengkonsolidasikan material). Contoh yang sangat baik diberikan di sini, "Bagian 3. Contoh dari salah satu trik yang kami ajarkan" ;
• untuk banyak tugas dengan data terstruktur, tautan [fitur rekayasa] + [SVM] + [kernel] "still cake";
• karena kehilangan Engsel dianggap cukup cepat, dapat ditemukan di Vowpal Wabbit (secara default).

Modifikasi algoritma:

Ada berbagai tambahan dan modifikasi pada metode vektor dukungan, yang bertujuan menghilangkan kerugian tertentu:

• Relevance Vector Machine (RVM)
• 1-norma SVM (LASSO SVM)
• SVM Regularized Ganda (ElasticNet SVM)
• Mesin Fitur Pendukung (SFM)
• Mesin Fitur Relevansi (RFM)

Sumber tambahan tentang SVM:

1. Kuliah teks oleh K.V. Vorontsov
2. Ringkasan E. Sokolov - 14.15.16
3. Sumber keren oleh Alexandre Kowalczyk
4. Pada habr ada 2 artikel yang ditujukan untuk svm:
   
   • Tahun 2010
   • 2018 tahun
5. Di github, saya dapat menyoroti 2 implementasi SVM keren di tautan berikut:
   
   • Algoritma ML dari pengembang dalam negeri
   • ML-Dari-Gores

Kesimpulan:

Terima kasih banyak atas perhatiannya! Saya akan berterima kasih atas komentar, umpan balik, dan tips.
Anda akan menemukan kode lengkap dari artikel ini di github saya .

ps Terima kasih yorko untuk tips merapikan sudut. Terima kasih kepada Aleksey Sizykh - departemen fisika dan teknologi yang sebagian berinvestasi dalam kode ini.