Selamat siang
Seperti yang dijanjikan dalam artikel pertama saya, saya ingin memperkenalkan Anda dengan salah satu metode untuk memecahkan sistem persamaan Diophantine. Tujuan artikel ini adalah untuk membiasakan pembaca lain dengan teknik ini dan menyampaikannya dengan cara yang kurang lebih dimengerti.
Pertimbangkan sistem dua persamaan Diophantine
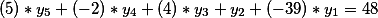
dan

Kami menemukan semua solusi yang mungkin untuk persamaan pertama. Bagaimana, Anda bertanya? Tentunya ada metode yang berbeda, tetapi saya akan berbagi di salah satu artikel berikut bagaimana saya akan memecahkan masalah yang sama. Sekarang, kami hanya berasumsi bahwa solusi umum memiliki bentuk

Bagaimana cara memastikan bahwa saya tidak bohong?
Cukup untuk mengingat kembali kalkulus matriks dan melipatgandakan vektor nilai dari persamaan Diophantine pertama kami (tanpa istilah bebas) dengan matriks semua koefisien .

diperoleh sebagai hasil nilai dari istilah bebas, dan oleh karena itu perhitungannya benar
Langkah selanjutnya adalah mengganti solusi bersama kami.

ke dalam persamaan kedua

Prosedurnya sama: kita mengalikan vektor dari koefisien persamaan kedua dengan solusi umum yang pertama
kami mendapatkan hasil ini
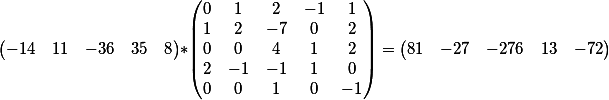
yaitu, kami mendapat persamaan bentuk
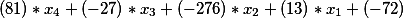
Di sisi kanan persamaan Diophantine kedua, karena ada istilah bebas sama dengan -335, ia tetap, yaitu, solusi akhir kami pada tahap ini memiliki bentuk
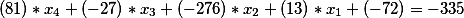
Atau memindahkan anggota gratis ke kanan yang kita dapatkan
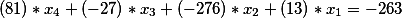
Jadi, kita mendapatkan persamaan Diophantine berikutnya. Mari kita temukan solusi umumnya dan mengujinya untuk kebenaran.

yaitu, solusi umumnya
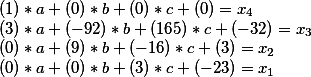
Dan sekarang kita sedang melakukan transformasi terbalik (biarlah demikian). Yaitu, sistem

Alih-alih tidak diketahui x kita mengganti apa yang terjadi pada tahap terakhir
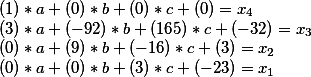
Dalam kalkulus matriks, ini diselesaikan dengan mengalikan satu matriks dengan yang lain.
Tetapi dengan matriks pertama, prosedur tertentu perlu dilakukan: menghapus (sementara) kolom terakhir dengan syarat bebas, karena parameter ini tidak berpartisipasi dalam perkalian, dan akan digunakan nanti.
Hasil dari mengalikan dua matriks menghasilkan
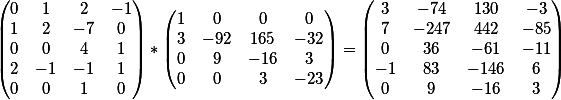
matriks
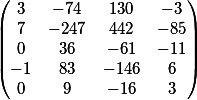
Kolom terakhir adalah anggota gratis dari sistem ini.
Kami memperhitungkan kolom yang dihapus sementara sebelum perkalian dan menambahkannya
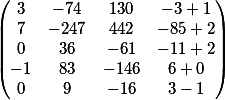
jawaban akhir kami dalam bentuk matriks
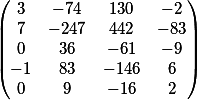
Lihat itu?
Produk vektor dari koefisien persamaan pertama dan matriks
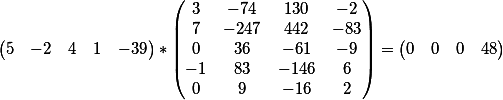
dan produk vektor dari koefisien persamaan kedua dan matriks
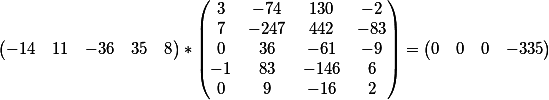
Seperti yang Anda lihat, hasilnya bertepatan dengan istilah bebas dari masing-masing persamaan.
Dengan demikian, solusi umum memiliki bentuk
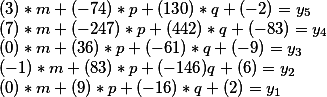
di mana m, p, q - dapat mengambil nilai integer
Sedemikian mudahnya, adalah mungkin untuk menyelesaikan persamaan diophantine linier yang lebih kompleks. Kalkulator yang sebenarnya dibuat setelah algoritma ini, kalkulator ini benar-benar tidak suka ketika nol muncul alih-alih nilai dalam koefisien dari persamaan pertama dari sistem awal. Tapi ini masalah implementasi khusus saya dari algoritma ini.
Dalam topik berikutnya, saya akan memberi tahu Anda cara membuat persamaan diophantine menggunakan matriks solusi umum. Tugas itu umumnya dangkal dan dilakukan dalam satu tindakan, tetapi tiba-tiba seseorang tidak tahu.
Saya akan berterima kasih atas komentar, umpan balik, dan saran.