Selama berabad-abad, para peneliti telah mencari contoh situasi di mana persamaan Euler untuk hidrodinamika fluida ideal terbukti salah. Dan akhirnya, ahli matematika menemukan contoh seperti itu.
Selama bertahun-tahun, matematikawan menduga bahwa dalam kondisi tertentu
persamaan Euler akan menolak untuk bekerja. Namun, mereka tidak dapat menggambarkan skenario khusus di mana ini terjadi. Sampai hari ini.
Persamaan ini adalah deskripsi matematis ideal gerakan fluida. Dalam asumsi tertentu, mereka memodelkan perambatan gelombang di kolam atau infiltrasi molase dari kaleng. Mereka harus bisa menggambarkan pergerakan cairan apa pun dalam kondisi apa pun - dan selama lebih dari dua abad, itu.
Namun, bukti baru menunjukkan bahwa dalam kondisi tertentu, persamaan ini masih menolak untuk bekerja.
"Setahun setengah yang lalu, saya akan mengatakan bahwa saya tidak berharap melihat perkembangan seperti itu bahkan selama hidup saya," kata
Tarek Elgindi , seorang ahli matematika dari University of California di San Diego, penulis sebuah karya baru.
Elgindi membuktikan adanya kekurangan dalam persamaan Euler dalam dua karya yang diterbitkan pada 2019 - ia menulis
April sendiri, dan
Oktober - bekerja sama dengan
Tejeddin Gole dan
Nader Masmudi . Pekerjaan itu membalikkan satu abad asumsi tentang persamaan terkenal untuk cairan ini.
"Saya pikir ini adalah pencapaian yang luar biasa dan luar biasa," kata
Peter Constantine , seorang ahli matematika di Universitas Princeton.
Karya Elgindi tidak mengantar pada akhir persamaan Euler. Ini membuktikan bahwa di bawah kondisi yang sepenuhnya pasti persamaannya tampak terlalu panas dan mulai memberikan omong kosong. Namun dalam kondisi yang lebih realistis, persamaan sejauh ini tetap kebal.
Namun, pengecualian yang ditemukan oleh Elgindi mengejutkan para ahli matematika, karena hal itu terjadi dalam kondisi di mana, seperti yang diperkirakan sebelumnya, persamaan harus tetap bekerja.
"Secara umum, menurut saya orang terkejut dengan contoh yang diberikan oleh Tarek," kata
Vlad Vikol , ahli matematika di New York University.
Bagaimana persamaan Euler mengalir
Leonhard Euler menurunkan persamaan untuk cairan yang sekarang memakai namanya pada 1757. Mereka menggambarkan evolusi cairan dari waktu ke waktu, sama seperti persamaan Newton menggambarkan pergerakan bola bilyar di atas meja.
Lebih tepatnya, persamaan ini menunjukkan gerakan seketika partikel infinitesimal cairan. Deskripsi mereka termasuk kecepatan partikel (seberapa cepat dan ke arah mana ia bergerak) dan jumlah yang terhubung dengannya sebagai
vortisitas (seberapa cepat partikel berputar dalam cara top, dan ke arah mana).
Semua informasi ini seluruhnya membentuk "bidang kecepatan", potret gerakan fluida pada titik waktu tertentu. Persamaan Euler dimulai dengan bidang kecepatan awal, dan memprediksi bagaimana itu akan berubah kapan saja di masa depan.
Tarek ElgindiPersamaan Euler tidak menggambarkan fluida dunia nyata secara harfiah. Ini termasuk beberapa asumsi non-fisik. Misalnya, mereka bekerja hanya jika aliran internal dalam fluida tidak menciptakan gesekan, bergerak relatif satu sama lain. Ketidakterkompresi cairan juga diasumsikan, yaitu, menurut aturan persamaan Euler, tidak mungkin untuk mengompres cairan, setelah menempatkannya dalam ruang volume yang lebih kecil daripada yang dibutuhkan.
"Model ini dapat dibayangkan sebagai dunia ideal, dan persamaan sebagai aturan untuk pergerakan dunia ini," tulis
Vladimir Sverak dari University of Minnesota kepada kami melalui email.
Kondisi yang tidak biasa ini memungkinkan ahli matematika dan fisika John von Neumann untuk bercanda menyatakan bahwa persamaan ini mensimulasikan perilaku "air kering". Untuk mensimulasikan fluida yang lebih realistis yang mengalami gesekan internal (yang disebut viskositas), para peneliti menggunakan
persamaan Navier-Stokes .
“Persamaan Euler sangat ideal. Gesekan hadir dalam cairan nyata, ”kata Konstantin.
Tetapi pada saat yang sama, persamaan Euler masih menempati tempat yang disegani dalam sains. Para peneliti ingin mengetahui apakah persamaan ini bekerja dengan jelas dalam kerangka dunia ideal ini tanpa gesekan dan kompresi - yaitu, apakah mereka dapat menggambarkan semua keadaan masa depan dari semua versi awal yang mungkin dari bidang kecepatan. Atau, dengan kata lain: apakah ada gerak yang sedemikian rupa sehingga persamaan ini tidak bisa model?
"Pada intinya, pertanyaannya sederhana: apakah persamaan ini selalu melakukan tugasnya?" Kata Sverak.
Secara teori, menggantikan dalam persamaan nilai-nilai dari keadaan saat ini cairan, Anda akan mendapatkan nilai yang tepat untuk menggambarkan keadaan di masa depan. Kemudian Anda dapat lagi mengganti nilai-nilai baru ini ke dalam persamaan, dan memperpanjang perkiraan Anda. Dan biasanya proses serupa dapat dilanjutkan untuk waktu yang lama di masa depan.
Namun, juga dimungkinkan bahwa dalam kondisi yang sangat jarang persamaannya pecah. Mereka dapat berderit, terengah-engah, menghasilkan nilai output yang cocok untuk peran parameter input di masa depan, dan kemudian tiba-tiba menghasilkan nilai yang sama sekali tidak cocok untuk mereka. Dalam kasus seperti itu, ahli matematika mengatakan bahwa persamaan "bergegas".
Jika persamaan Euler tergesa-gesa, itu karena mereka mulai meningkatkan kecepatan atau vortisitas titik dengan cara yang tidak wajar. Keuntungan ini akan sangat kuat sehingga dalam waktu yang terbatas kecepatan atau pusaran suatu titik menjadi tak terbatas. Dan segera setelah persamaan memberikan nilai tak terbatas, mereka akan rusak dan berhenti menggambarkan kondisi lingkungan di masa depan. Ini karena biasanya tidak mungkin untuk melakukan perhitungan dengan nilai tak terhingga - ini sama dengan membagi dengan nol (ngomong-ngomong, nilai kecepatan dalam hal ini akan melebihi kecepatan cahaya - meskipun di dunia model yang ideal ini bukan yang terburuk).
Makna tak terbatas yang ditakdirkan ini disebut "singularitas." Ketika ahli matematika bertanya, "Apakah persamaan Euler selalu bekerja?", Mereka benar-benar bertanya "apakah ada skenario di mana persamaan Euler memberikan singularitas?"
Banyak ahli matematika percaya bahwa - ada, sampai saat ini, mereka tidak dapat menemukan skenario khusus di mana persamaan benar-benar meledak.
"Ada perasaan bahwa Euler berusaha menghindari singularitas, dan sampai baru-baru ini, ia berhasil," kata Konstantin.
Karya baru tidak menunjukkan bagaimana persamaan memberikan singularitas dalam kondisi yang paling diminati matematikawan. Namun, sejauh ini hasil ini telah mendekati tujuan daripada sisanya. Dan untuk ini, Elgindi dianggap sebagai model gerak fluida yang disederhanakan.
Mengurangi kompleksitas
Matematikawan memiliki banyak cara berbeda untuk mengurangi kerumitan gerak fluida, untuk simulasi yang mereka gunakan persamaan Euler. Banyak hasil yang paling menarik, mirip dengan yang dicapai oleh Elgindi, termasuk demonstrasi seberapa banyak Anda dapat menyederhanakan perilaku fluida - yaitu, seberapa banyak Anda dapat menyederhanakan data yang disubstitusi ke dalam persamaan - sambil tetap bisa mengatakan sesuatu yang bermakna tentang persamaan itu sendiri.
Dalam fluida tiga dimensi yang nyata, seperti air di kolam, setiap partikel memiliki tiga sumbu yang memungkinkan untuk bergerak: sumbu x (kiri-kanan), sumbu y (atas-bawah), dan sumbu z (maju-mundur). Cukup banyak kebebasan bergerak. Terlebih lagi, pergerakan partikel dalam satu bagian cairan tidak selalu terkait kuat dengan pergerakan partikel di bagian lain.
"Kamu harus melacak terlalu banyak," kata Elgindi.
Dalam makalah baru, Elgindi menyederhanakan pekerjaan untuk persamaan Euler. Ini mensyaratkan bahwa cairan harus simetris di sepanjang sumbu z, yang biasanya tidak ditemukan dalam cairan nyata. Karena simetri, menjadi lebih mudah untuk menghitung bidang kecepatan, karena diketahui bahwa titik-titik di kedua sisi sumbu z adalah simetris cermin. Oleh karena itu, jika Anda mengetahui kecepatan atau vortisitas dari satu titik, Anda hanya perlu mengubah tanda nilai-nilai ini, dan mendapatkan nilai-nilai ini untuk titik lain.
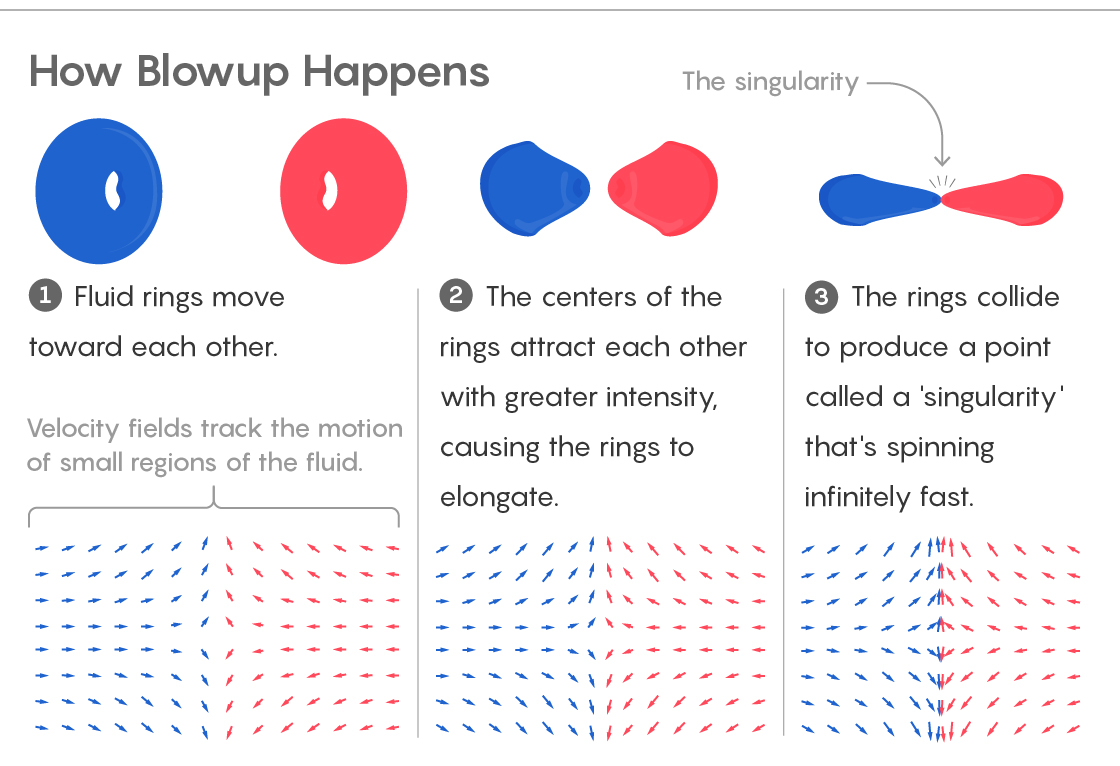1) Cairan bergerak menuju. Bidang kecepatan melacak pergerakan bagian-bagian kecil fluida.
2) Bagian tengah cincin tertarik, yang menyebabkan cincin meregang.
3) Cincin bertabrakan, menciptakan titik "singularitas", berputar dengan kecepatan tak terbatas.Ini juga membatasi kemungkinan pergerakan titik dalam fluida. Partikel dapat dipindahkan di sepanjang sumbu z, atau menjauh dari itu, atau ke arahnya. Mereka tidak dapat berputar di sekitar sumbu z. Matematikawan mengatakan bahwa tidak ada pusaran air dalam cairan semacam itu.
"Ini mengurangi tugas menjadi dua dimensi," kata Elgindi.
Akhirnya, Elgindi memberlakukan beberapa kondisi lebih pada data awal yang dimasukkan ke dalam persamaan Euler. Dalam beberapa hal, data ini lebih kasar daripada yang menggambarkan cairan nyata, dan meningkatkan kemungkinan pembentukan singularitas.
Dalam kehidupan nyata, jika Anda berpindah dari satu titik ke titik lain, yang terletak sangat dekat dengannya, maka kecepatan kedua titik ini akan hampir sama. Vortisitas dari kedua poin ini juga harus sangat mirip. Matematikawan mengatakan bahwa bidang kecepatan dengan properti ini “halus”, yaitu, nilai pada mereka berubah secara bertahap - atau lancar - ketika bergerak dari satu titik ke titik lainnya. Tidak ada perubahan cepat.
Tetapi dalam hal deskripsi cairan dari Elgindi, semuanya berbeda.
"Perputaran dalam data Tarek dapat banyak berubah," kata Vikol. "Poin yang dekat bisa memiliki vortisitas yang sangat berbeda."
Tampaknya penyederhanaan Elgindi sangat berbeda dengan perilaku cairan nyata agar bermanfaat. Namun, mereka masih jauh lebih kaku daripada banyak skenario yang disederhanakan di mana para ilmuwan sebelumnya dianggap persamaan Euler. Bahkan, Elgindi bahkan menunjukkan bahwa di bawah kondisi yang disederhanakan - tapi tidak terlalu banyak ini - persamaan Euler mulai menghasilkan hasil yang sangat tak terduga.
Game usai
Untuk memahami penemuan Elgindi, bayangkan sebuah wadah berisi air. Ini bukan contoh yang tepat, karena karya Elgindi menganggap cairan yang tidak memiliki batas, yaitu terbang seperti gelembung tanpa gravitasi. Tetapi untuk memvisualisasikan naskah, yang merupakan pusat karyanya, akan berguna untuk mengatur air di dalam tangki. Meskipun hipotesis matematika yang paling penting - dan yang paling sulit dibuktikan - menyangkut cairan tanpa batas.
Lalu bayangkan dua cincin air tebal yang terletak di ujung tangki yang berbeda. Mereka membentuk corong kecil, seperti pusaran air - gangguan terorganisir di dalam cairan. Fenomena serupa ditemukan di alam, dan mirip dengan cincin asap yang dapat diberikan oleh perokok.
Sekarang bayangkan bagaimana dua cincin yang berlawanan bersatu.
Selama pendekatan, persamaan Euler bekerja secara normal, menghitung bidang kecepatan yang menggambarkan fluida pada setiap saat dalam waktu. Tetapi ketika mereka saling berdekatan, persamaan mulai menghasilkan hasil yang sangat aneh.
Mereka menunjukkan bagaimana cincin mulai tertarik satu sama lain lebih banyak dan lebih banyak lagi - dan titik-titik utama dari cincin-cincin tersebut saling tertarik bahkan lebih daripada bagian luarnya. Akibatnya, cincin diperpanjang, dan mulai menyerupai corong. Dan semakin banyak pusat cincin semakin dekat, semakin tinggi kecepatannya. Dan kemudian mereka bertabrakan.
Dan jika pada saat ini Anda melihat bidang kecepatan yang menggambarkan tabrakan, Anda dapat melihat bahwa dengan serangkaian asumsi ini dalam seluruh sejarah persamaan Euler, tidak ada yang melihat: singularitas. Elgindi membuktikan bahwa persamaan Euler memberikan kecepatan tak terbatas pada titik tabrakan. Game sudah berakhir.
"Bentuk klasik dari persamaan itu pecah," kata Elgindi. "Setelah itu, tidak jelas apa yang sedang terjadi."
Hasilnya memiliki keterbatasan. Yaitu, tidak mungkin untuk meramalkan perilaku persamaan Euler dalam kondisi yang benar-benar "halus" berdasarkan hasil ini. Matematikawan beberapa dekade yang lalu membuktikan bahwa dalam kondisi "halus", skenario yang dipertimbangkan oleh Elgindi tidak akan menghasilkan singularitas.
Namun, sisa hasilnya benar-benar mengubah pandangan ahli matematika pada persamaan lama ini.
Sebelum karya Elgindi, matematikawan tidak dapat membuktikan keberadaan situasi apa pun dalam suatu cairan tanpa batas, di mana persamaan Euler bekerja untuk beberapa waktu (sementara cincin-cincin itu bersatu), tetapi tidak tanpa batas. Dalam semua karya sebelumnya, ahli matematika ternyata bahwa jika persamaan pada dasarnya bekerja, maka mereka selalu bekerja.
"Ini adalah hasil yang sangat luar biasa, karena membuktikan keberadaan singularitas dalam skenario, yang kami sebut 'didefinisikan dengan benar.'" Masuk akal, tetapi pada saat yang sama kita sampai pada singularitas dalam waktu yang terbatas, ”kata Konstantin.
Banyak generasi ilmuwan telah mencari titik lemah dalam persamaan Euler. Dan akhirnya - dengan beberapa keberatan - ahli matematika menemukannya.