Tentang makna geometris kode Gray

Kode abu-abu memiliki hubungan dekat dengan kurva Hilbert .

Namun, ketika berkomunikasi dengan rekan kerja ternyata kecanduan sederhana ini terlihat di mata mereka sebagai sesuatu yang tidak sepele. Pencarian Internet begitu saja tidak memberikan apa pun kecuali ungkapan berlumpur pada wiki: "Kurva Hilbert di ruang dimensi yang lebih besar adalah perwakilan dari generalisasi kode Gray". Karena itu, ada keinginan untuk membuka topik - secara singkat, dalam bahasa yang sederhana.

Akibatnya, di bawah luka - "skandal, intrik, investigasi".

Fitur utama dari kode Gray adalah bahwa dua nilai yang berdekatan secara leksikografis berbeda hanya dalam satu kategori. Di sisi lain, kurva Hilbert kontinu - jarak antara dua titik yang berdekatan selalu satu. Ini saja mengisyaratkan koneksi batin mereka.

Kode Gray menggambarkan kemunculan kurva Hilbert dalam satu hypercube. Bahkan, jika kita mengambil kode 3-bit dan menggambarnya dalam ruang 3 dimensi (mengambil setiap bit untuk koordinat yang sesuai), kita mendapatkan


Gambar 1 Kode abu-abu 3-bit sebagai kubus 3 dimensi

Gambar yang sudah dikenal adalah simpleks 3 dimensi dari kurva Hilbert! Berhasil mengganti setiap simpul simpleks dengan simpleks yang sama (dengan mempertimbangkan rotasi dan refleksi akun untuk mempertahankan kontinuitas), kami memperoleh kurva Hilbert 4x4x4.

Melanjutkan iterasi ini, kita dapat terus mengisi kisi kubik dengan berbagai ukuran.


Gambar 2 beberapa iterasi simpleks kurva Hilbert.

Tetapi bagaimana itu bisa terjadi?

Diketahui bahwa kode Gray hampir sama. Kadang-kadang disebut mirror “karena fakta bahwa bagian pertama dari nilai ketika mengubah urutan setara dengan bagian kedua, dengan pengecualian bit tinggi. Bit yang paling signifikan hanya terbalik. " Untuk kejelasan, kode 3-bit adalah bit paling signifikan - paling kiri:



Karena kita berbicara tentang kemiripan diri, mari kita mulai dari awal - dengan kode satu-bit. Sebenarnya, mungkin untuk memulai dengan dimensi nol - poin, ini pada dasarnya tidak mengubah apa pun, hanya kata-kata yang harus ditulis lebih banyak.

Kode single-digit Gray bahkan lebih sederhana daripada senapan tiga-baris, bisa 0 atau 1.

Secara geometris, ini sesuai dengan satuan kubus satu dimensi - segmen. Anda dapat bergerak sepanjang segmen baik dari awal hingga akhir, atau dari ujung ke awal - hingga simetri, ini satu dan sama. Namun demikian, kita akan menyebut awal tempat di mana nilainya kurang (ingat bahwa sisi kubus adalah digit dari angka), dan akhirnya - di mana lebih banyak.

Kami beralih ke kasus dua dimensi. Kubus dua dimensi adalah kotak. Dengan mempertimbangkan kesamaan diri, kami mengkloning kubus satu dimensi (0,1) dan mendapatkan dua segmen - (0,0 -> 1,0) dan (0,1 -> 1,1). Sekarang Anda perlu menghubungkan segmen-segmen ini untuk berkeliling. Dan di sini muncul dua opsi:

• kita menghubungkan awal iterasi sebelumnya - kubus satu dimensi dengan awal klonnya. Hingga simetri, ini sama dengan menghubungkan ujung ke ujung. Jenis simetri adalah cermin. Opsi ini secara kondisional disebut "misionaris".
  
• kami menghubungkan ujung iterasi sebelumnya dengan awal klonnya. Hingga simetri, ini sama dengan menggabungkan awal garis dengan ujung klon. Jenis simetri adalah pusat. Kami menyebut opsi ini "kereta".

Kami bertindak serupa dengan melewatkan tiga kasus dimensional atau lebih.


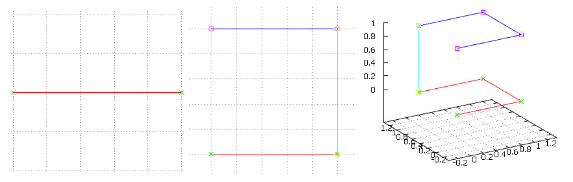Gambar 3 Dua iterasi pertama dari versi "misionaris"

Di sini iterasi sebelumnya disorot dalam warna merah, klonnya berwarna biru, dan koneksi mereka dalam pirus.

Perhatikan bahwa koneksi selalu melewati dimensi tunggal - yang baru ditambahkan, karenanya fitur utama dari kode Gray muncul karena kemiripan diri. Dan karena akhir dari iterasi sebelumnya terhubung dengan ujung klonnya, "mirroring" terjadi - ketika berkeliling, kita dipaksa untuk melalui klon dalam urutan terbalik. Terlepas dari dimensi. Di sini Anda dapat melihat asal-usul dan fitur kurva Hilbert - tidak peduli seberapa besar kisi (dari dimensi apa pun), pada tingkat akar rumput masih merupakan unit kubus yang sama dengan transisi panjang satu.


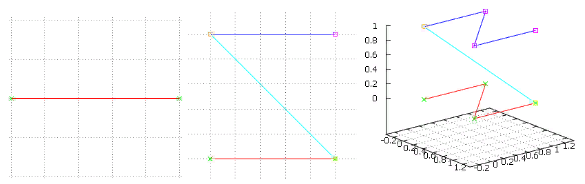Gambar 4 Dua iterasi pertama dari opsi "kereta", warna yang sama

Tapi musik ini juga akrab bagi kita - kita punya kurva Z simpleks. Kata simplex di sini juga berarti bahwa jika kita mengambil masing-masing poin dan menggantinya dengan simpleks, kita mendapatkan kubus 4x4x4, melanjutkan iterasi - kita dapat mengisi kisi kubik besar yang sewenang-wenang.

Sangat lucu bahwa dalam kasus ini, konversi jalur yang dilewatkan dari asal ke kode, yang dapat diurai menjadi bit, adalah sepele.
Sedangkan kasus kode Gray adalah G = W ^ (W >> 1), di mana W adalah panjang yang dilewati, G adalah kode Gray.


Gambar 5 dua iterasi pertama dari kurva Z (wiki)


6 untuk perbandingan, dua iterasi pertama dari kurva Hilbert (wiki)

Tetapi tidak ada pilihan (alami) lain untuk menghindari hypercube tunggal.
Jadi ternyata di mana pun Anda melempar, di sekitar Hilbert, Lebesgue ... dan kekosongan .

PS : dalam gambar judul, enkoder melingkar dengan kode Gray delapan digit.
PPS : di sini mereka mengoreksi saya bahwa simpleks adalah istilah yang mapan, tidak baik dengan itu. Nah, artikel ini bukan hanya simpleks, tetapi simpleks kurva Hilbert atau simpleks kurva-Z. Semoga matematikawan yang setia memaafkan saya.