Model manajemen program otomatis

1. Pendahuluan

Dalam [1], jawaban diberikan untuk pertanyaan tentang apa yang dianggap pemrograman otomatis (AP), tetapi model mesin keadaan terbatas (SC) tidak dijelaskan secara rinci sebagai model kontrol program otomatis. Jelas bahwa otomat abstrak murni tidak cocok untuk peran ini, karena dibatasi oleh jumlah saluran. Tetapi model struktural otomat, serta teori automata struktural yang sesuai dengannya, belum memungkinkan untuk memberikan jawaban tentang pilihan model otomat.

Masalahnya dimulai dengan fakta bahwa di antara banyak karya pada teori finite automata (TCA) ada beberapa yang memberikan definisi model struktural otomat terbatas (SCA). Benar, orang dapat memahami bahwa otomat struktural adalah diagram [struktural] automata elementer (elemen fungsional) yang mengimplementasikan model otomat abstrak [2]. Ingatlah bahwa, sesuai dengan teori, semuanya dimulai dengan membuat model perangkat dalam bentuk otomat abstrak, dan kemudian tugasnya adalah mensintesis sirkuit digital yang mengimplementasikannya [3].

Pemrograman sekilas tampak sedikit seperti sintesis sirkuit digital. Tapi baru pada awalnya. Pertama, di sana dan di sana semuanya dimulai dengan suatu algoritma. Kedua, masalah struktural pengorganisasian dan implementasi sirkuit digital dan pemrograman memiliki banyak kesamaan, terutama dalam konteks pemrograman paralel. Tetapi kita akan membahas topik paralelisme secara terpisah. Sementara itu, tugas kita adalah memilih dan / atau memodifikasi model mesin negara yang terbatas, yang dapat dimengerti, nyaman, dan menyenangkan bagi para programmer yang dimanjakan oleh berbagai perangkat lunak.

Benar, pertanyaannya langsung logis - mengapa ada satu "toolkit otomatis" yang agak tidak biasa? Kami akan mencoba menjawab pertanyaan ini dengan mendefinisikan model kendali otomatis [bersarang], dengan mempertimbangkan juga kelebihannya dibandingkan dengan model pemrograman yang biasa.

2. Definisi model kontrol program otomatis

Dalam proses evolusi, praktik pemrograman telah membentuk persyaratan tertentu untuk model manajemen program. Harus diakui bahwa model mesin negara terbatas klasik hanya sedikit bersesuaian dengan mereka. Dan jika tugasnya adalah menggunakan automata dalam pemrograman, maka itu perlu diadaptasi. Sangat diinginkan untuk melakukan ini dalam kerangka teori automata. Klaim utama terhadap AP yang ada dikurangi menjadi fakta bahwa kondisi ini dilanggar.

Definisi 1. Kita menyebut bentuk normal disjunctive normal finite automata (DNKA) finite automata yang terdefinisi penuh yang transisinya dilabeli oleh konjungsi elementer variabel logis.

Model DNA didasarkan pada model formal automata yang sepenuhnya (sepenuhnya) didefinisikan dengan keadaan abstrak [4] dan automata logis [5].

Definisi 2. Kami menyebut bentuk disjungtif a finite automaton (DFA) sebagai automaton dalam bentuk DFA yang hanya berisi transisi yang dihasilkan .

Transisi yang ditandai dengan sinyal keluaran dan transisi dengan tanda di tempat sinyal keluaran yang mengubah keadaan saat ini dari automaton diklasifikasikan sebagai transisi yang efektif. Transisi yang tidak termasuk dalam deskripsi otomat disjungtif merupakan tambahan dari DKA (DDA) ke otomat DFA yang didefinisikan sepenuhnya. Penambahan semacam itu adalah otomat yang terdiri dari keadaan terisolasi dengan transisi dalam bentuk loop dan dengan tanda hubung di tempat sinyal keluaran.

3. Model memori untuk model perhitungan AP

Kehadiran banyak input dan output DFA menetapkan paralelisme operator perangkat lunak / fungsi yang terkait dengannya. Untuk implementasinya yang benar, diperlukan model memori tipe CREW (concurrent read Exclusive - write) [6]. Dalam kerangka kerjanya, pembacaan nilai data saat ini diperbolehkan pada bagian dari set semua fungsi (predikat dan tindakan), dan hanya satu dari mereka yang diizinkan untuk mengubah data umum untuk tindakan paralel yang dapat dieksekusi.

Model kontrol otomatis, berbeda dengan model komputasi multi-threaded, jelas membatasi eksekusi operator / fungsi program otomatis hingga batas siklus waktu diskrit. Dalam situasi seperti itu, setiap perubahan pada memori dengan tindakan yang dilakukan pada siklus jam saat ini dapat ditulis ke "memori bayangan" , sehingga setelah selesai dan sebelum dimulainya siklus jam diskrit berikutnya, itu menjadi nilai-nilai baru.

Interaksi operator program otomat dengan memori akan disebut model memori bayangan . Model ini merupakan bagian penting dari model umum pemrograman otomatis. Ini memastikan kebenaran operasi paralel dari operator AP dan menyederhanakan pemrograman proses paralel.

Dalam kerangka model memori, mekanisme yang kompleks dan tidak terlalu andal untuk sinkronisasi multi-threaded dari proses sebenarnya tidak diperlukan (untuk lebih jelasnya lihat [7]). Tetapi jika perlu, karena kesetaraan automata dan grafik-skema algoritma (GAW) [8], model pemrograman otomatis tidak membatasi aplikasi mereka.

4. Model automata yang bersarang dan inersia

Tugas menciptakan model elemen logika penundaan, dipilih lebih lanjut sebagai contoh, di satu sisi, menunjukkan masalah model klasik otomat, dan, di sisi lain, mencerminkan kualitas model DFA yang menyelesaikan masalah algoritmik dengan cara yang lebih visual dan nyaman. Model diperkenalkan automata bersarang menghasilkan subkelas model otomat, selanjutnya disebut sebagai automata inersia , dan subkelas yang sesuai dari algoritma inersia .

Jadi, biarlah tugas menciptakan model diskrit dari elemen logika tunda yang mengimplementasikan transmisi sinyal input biner. Selain itu, waktu penundaan t01 dan t10, masing-masing, ke unit dan keadaan nol dalam kasus umum tidak bersamaan.

Model paling sederhana dari keterlambatan tunggal dalam bentuk otomat Mealy ditunjukkan pada Gambar. 1 (lihat, untuk perbandingan, model keterlambatan dalam [2]). Penundaannya ditentukan oleh satu siklus clock diskrit tunggal. Model penundaan transportasi yang lebih kompleks (untuk rincian lebih lanjut tentang jenis keterlambatan lihat [9]) dalam bentuk otomat Miley dan model Miley-Moore gabungan disajikan, masing-masing, pada Gambar. 2a dan ara. 2b.


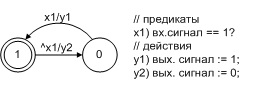
Fig. 1. Model unit delay dalam bentuk otomat Miles


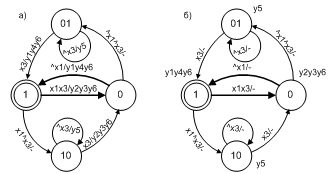
Fig. 2. Model keterlambatan transportasi Miles (a) dan Miles-Moore (b)

Sinyal input x3 (kita ingat bahwa dalam program otomatis ini sesuai dengan predikat [1]) mengambil nilai sebenarnya jika nilai penghitung jam sama dengan nilai variabel t sama dengan penundaan t01 atau t10. Nilai variabel t ditugaskan untuk sinyal y3 dan y4 (dalam program, fungsi aksi dengan nama yang sama dengan sinyal output). Sinyal y1, y2 mengatur nilai variabel yang mewakili output model. Sinyal y5 menambah penghitung jam, yang diatur ulang oleh sinyal y6.

Catatan 2. Keadaan internal model pada Gambar. 1, akan lebih mudah untuk diasosiasikan dengan status keluaran suatu elemen. Ini memungkinkan kita untuk mengecualikan tidak hanya operator y1 dan y2, tetapi juga variabel output itu sendiri.

Implementasi penanaman automata mirip dengan memanggil subrutin membentuk teknologi pemrograman otomat modular. Pada saat yang sama, di tingkat perangkat lunak, berbeda dengan upaya serupa di tingkat perangkat keras (lihat [10] untuk perbandingan), ini jauh lebih sederhana. Untuk melakukan ini, Anda harus memasukkan panggilan program dari nested automaton, dan kemudian kernel dari implementasi automata, seperti prosesor normal, mengatur pengembalian kontrol ke level saat ini untuk bersarang.

Definisi 3. Automata bersarang akan disebut automata dengan keadaan akhir, transisi yang memulai prosedur kembali ke tingkat (peringkat) bersarang sebelumnya.

Implementasi yang benar dari bersarang automata memberlakukan batasan pada prosedur untuk pembuatannya. Pertama, automaton bersarang hanya bisa berada di bawahnya. Selain itu, otomat tingkat atas, tidak termasuk peringkat nol, juga bisa menjadi otomat bersarang. Kedua, pada setiap transisi hanya satu automaton bersarang dapat dibuat. Mekanisme nested automata juga menciptakan dasar untuk penerapan algoritma rekursif berdasarkan kontrol otomatis.


Fig. 3. Model keterlambatan dalam bentuk automata bersarang

Gambar. 3 menunjukkan model penundaan, di mana Gambar. 3a mewakili model tingkat atas, dan Gambar. 3b dan Gambar. 3c - varian automata bersarang untuk transportasi dan penundaan inersia (untuk detail lebih lanjut tentang jenis penundaan lihat [8]). Pada saat yang sama, ini adalah contoh dari dua jenis automata bersarang - biasa dan inersia . Jenis otomat bersarang ditentukan oleh nama status akhirnya: keadaan dengan nama "00" menentukan jalan keluar yang biasa dari otomat bertingkat, dan keadaan dengan nama "XX" tidak mengubah keadaan saat ini dari otomat tingkat atas.

Penjelasan penting untuk memahami algoritma penundaan inersia. Untuk itu (lihat Gbr. 3c), nilai predikat x1 tergantung pada transisi tempat automaton tertanam dibuat. Dengan kata lain, predikat dalam status "0" mengontrol pelestarian "nol" pada input, dan pada kondisi "1", sebaliknya, "unit". Jika nilai pada input adalah nol pada nilai nol dari output, maka Anda harus mengembalikan nilai sebenarnya. Lebih lanjut, jika stabilitas input dilanggar (nilai x1 salah) dan waktu tunda belum kedaluwarsa (nilai x3 salah), maka jalan keluar dari mesin tertanam direalisasikan melalui keadaan inersia (lihat Gambar 3c).

Definisi 4. Automata, termasuk panggilan automata bersarang yang memiliki keadaan inersia akhir, akan disebut automata inersia .

Dalam model pada Gambar. 3a, tindakan z1 (simbol z dipilih untuk nama-nama tindakan yang mencakup panggilan ke robot bersarang) membuat robot bersarang jika nilai penundaan ditentukan. Sebagai bagian dari tindakan ini, jenis penundaan yang ditentukan ditentukan, sesuai dengan yang dibuat oleh salah satu automata bersarang, ditunjukkan pada Gambar.3b atau Gambar. 3c.

Pada tingkat atas hierarki, pandangan otomat pada Gambar. 3a benar-benar bertepatan dalam struktur dengan model pada Gambar. 1, berbeda hanya dengan adanya tindakan pada transisi. Penundaan dengan nata automata memiliki bentuk yang lebih sederhana dibandingkan dengan model tingkat tunggal pada Gambar. 2. Otomat bersarang juga dapat dianggap sebagai semacam "otomat perpustakaan" yang dapat dipanggil dari otomat lain.

3. Pemrograman otomat objek

Model kontrol otomatis, selain bentuk grafik, juga memiliki bentuk tabel sederhana - tabel transisi (TP), yang dapat secara efektif ditafsirkan dalam C ++. Dalam kerangka kerjanya, program otomat terpisah (atau bagian darinya) dan, dengan demikian, definisinya dalam bentuk rangkaian program S dapat diwakili oleh kelas. Dalam hal ini, model memori akan sesuai dengan properti kelas, rangkaian operasi akan sesuai dengan metode kelas, dan kontrol otomatis dalam bentuk TP akan menggambarkan perilaku kelas. Pengenalan kontrol ke dalam kelas memungkinkan kita untuk berbicara tentang objek aktif, juga sering disebut agen, dll.

Banyak objek dengan perilaku dalam bentuk kontrol otomat memformalkan konsep program paralel otomat objek . Dalam hal ini, model dari setiap program paralel dapat diwakili oleh diagram program di mana kontrol C akan disajikan dalam bentuk jaringan otomat, di mana komponen automata menggambarkan perilaku objek aktif, memori M diwakili oleh kombinasi sifat-sifat objek, dan banyak operator A diwakili oleh kombinasi metode objek program.

Dalam lingkungan VKPA, peran bahasa pemrograman otomatis ditugaskan ke bahasa C ++. Dalam "C ++ otomatis", objek diberkahi dengan aktivitas / perilaku dan memiliki cara untuk menggambarkan dan menerapkan paralelisme, baik pada tingkat metode objek individu maupun pada tingkat menggambarkan operasi paralel banyak objek.

Implementasi objek AP yang ada agak rumit. Dalam VKPa, implementasi objeknya didasarkan pada interpretasi automata dan kontrol khusus program. Tidak seperti implementasi langsung automata, yang digunakan, misalnya, dalam teknologi SWITH, ini menghilangkan prosedur untuk mengubah model otomat menjadi model diagram alur. Algoritma interpretasi yang digunakan dalam VKPa mirip dengan metode menafsirkan tabel keputusan oleh E. Hamby [12].

Kecuali ditentukan lain, kami selanjutnya akan mengaitkan konsep program otomat dengan konsep objek otomat (AO) dalam arti OOP, tetapi dengan mempertimbangkan konsep program paralel objek otomat yang diperkenalkan di atas. Karena itu, operator dan memori AP akan ditentukan melalui metode dan properti objek yang aktif. Objek automata dibedakan dari objek biasa dengan keberadaan perilaku yang ditentukan oleh model mesin negara.

4. Kesimpulan

Membuat model automata bersarang adalah langkah menuju perubahan kualitatif dalam teknologi pemrograman. Model inersia otomat yang dideskripsikan mirip dengan konsep status historis dalam UML. Embedding automata yang biasa memiliki analog dalam pemrograman, "embedding inersia" tidak memilikinya, karena Dalam suatu program, Anda tidak dapat kembali ke perintah sebelum panggilan subrutin. Dan ini adalah elemen perbedaan kualitatif antara pemrograman otomatis dan pemrograman biasa.

Anda tentu saja dapat memperkenalkan memori bayangan ke dalam pemrograman biasa dan menunjukkan paralelisme fungsi. Tetapi dalam kerangka model otomat, semua ini memiliki bentuk organik, baik dalam hal deskripsi maupun dalam hal kinerja. Semuanya ditentukan oleh paralelisme alami model. Model diagram blok tidak memiliki kemampuan seperti itu.

Objek aktif juga memperluas kemampuan pemrograman. Tetapi "pembungkus objek", untuk bagiannya, secara kualitatif mempengaruhi pemrograman otomatis, menyederhanakan prosedur untuk memohon dan mengimplementasikan automata bersarang. Jadi, penggunaan properti kelas [lokal] memungkinkan Anda untuk mengimplementasikan tidak hanya penyematan, tetapi juga algoritma rekursif.