Teori Informasi Visual (Bagian 2)

Bagian kedua dari terjemahan Longrid dikhususkan untuk visualisasi konsep dari teori informasi. Bagian kedua berkaitan dengan entropi, cross entropy, divergensi Kullback-Leibler, informasi timbal balik dan bit fraksional. Semua konsep dilengkapi dengan penjelasan visual yang sangat baik.

Untuk kelengkapan, sebelum membaca bagian kedua, saya sarankan Anda membiasakan diri dengan yang pertama .

Perhitungan Entropi

Ingat bahwa biaya pesan panjang $$$L$ sama dengan $$$\ frac {1} {2 ^ L}$ . kita dapat membalikkan nilai ini untuk mendapatkan panjang pesan yang sepadan dengan jumlah yang diberikan: $$$\ log_2 (\ frac {1} {cost})$ . Karena kita menghabiskan $$$p (x)$ per codeword untuk $$$x$ , panjangnya akan sama $$$\ log_2 (\ frac {1} {p (x)})$ . Pada gambar, pilihan panjang kata sandi terbaik.



Kami telah membahas sebelumnya bahwa ada batas mendasar seberapa pendek pesan rata-rata dapat untuk menyampaikan peristiwa dari distribusi probabilitas yang diberikan $$$p$ . batas ini, panjang pesan rata-rata saat menggunakan sistem pengkodean terbaik, disebut entropi $$$p, H (p)$ . Sekarang kita tahu panjang kata sandi optimal, kita bisa menghitungnya!

$$

$$H (p) = \ sum_xp (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

(Seringkali, entropi ditulis sebagai $$$H (p) = - \ jumlah p (x) \ log_2 (p (x))$ menggunakan kesetaraan $$$\ log (1 / a) = - \ log (a)$ . Sepertinya saya bahwa versi pertama lebih intuitif, jadi kami akan terus menggunakannya.)

Jika saya ingin melaporkan peristiwa apa yang terjadi, maka apa pun yang saya lakukan, rata-rata saya perlu mengirim begitu banyak bit.

Jumlah rata-rata informasi yang diperlukan untuk mengirimkan sesuatu memiliki konsekuensi langsung untuk kompresi. Tetapi adakah alasan lain mengapa kita harus mengurus ini? Ya! Ini menggambarkan ketidakpastian saya, dan memungkinkan untuk mengukur informasi.

Jika saya tahu pasti apa yang akan terjadi, saya tidak perlu mengirim pesan sama sekali! Jika ada dua hal yang dapat terjadi dengan probabilitas 50%, saya hanya perlu mengirim 1 bit. Tetapi jika ada 64 peristiwa berbeda yang dapat terjadi dengan probabilitas yang sama, saya harus mengirim 6 bit. Semakin terkonsentrasi probabilitas, semakin banyak peluang yang saya miliki untuk membuat kode pintar dengan pesan pendek menengah. Semakin kabur probabilitasnya, semakin lama posting saya seharusnya.

Semakin tidak pasti hasilnya, semakin saya belajar rata-rata ketika mereka memberi tahu saya apa yang terjadi.

Cross entropy

Sesaat sebelum pindah ke Australia, Bob menikahi Alice, juga imajiner. Yang mengejutkan saya, juga mengejutkan karakter lain di kepala saya, Alice bukan pecinta anjing. Dia adalah pecinta kucing. Meskipun demikian, mereka dapat menemukan bahasa yang sama dalam obsesi umum mereka dengan hewan dan kosa kata mereka yang sangat terbatas.



Keduanya menggunakan kata-kata yang sama, hanya dengan frekuensi yang berbeda. Bob berbicara tentang anjing setiap saat, Alice berbicara tentang kucing setiap saat.

Alice pertama-tama mengirimiku pesan menggunakan kode Bob. Sayangnya, postingnya lebih lama dari yang dibutuhkan. Kode Bob telah dioptimalkan untuk distribusi probabilitasnya. Alice memiliki distribusi probabilitas yang berbeda, dan kodenya tidak optimal untuknya. Panjang codeword rata-rata ketika Bob menggunakan kodenya adalah 1,75 bit, ketika Alice menggunakannya, maka 2,25. Akan lebih buruk jika keduanya tidak begitu mirip!

Panjang pesan rata-rata dari satu distribusi dengan kode optimal untuk distribusi lain disebut cross-entropy. Secara formal, kita dapat mendefinisikan entropi silang sebagai berikut:

$$

$$H_p (q) = \ sum_xq (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

Dalam hal ini, kita berbicara tentang entropi silang dari frekuensi kata catworm Alice sehubungan dengan frekuensi kata dari pecinta anjing Bob.



Untuk mengurangi biaya koneksi kami, saya meminta Alice untuk menggunakan kode sendiri. Saya lega, ini mengurangi panjang pesan rata-rata. Tetapi ini menciptakan masalah baru: terkadang Bob secara tidak sengaja menggunakan kode Alice. Anehnya, lebih buruk ketika Bob menggunakan kode Alice daripada ketika Alice menggunakan kode Bob!

Jadi sekarang kita memiliki empat kemungkinan:

• Bob menggunakan kode asli ( $$$H (p) = 1,75$ bit)
• Alice menggunakan kode Bob ( $$$H_p (q) = 2,25$ bit)
• Alice menggunakan kodenya sendiri ( $$$H (q) = 1,75$ bit)
• Bob menggunakan kode Alice ( $$$H_q (p) = 2.375$ bit)

Ini tidak seintuitif yang mungkin orang pikirkan. Sebagai contoh, kita dapat melihatnya $$$H_p (q) ≠ H_q (p)$ . Bisakah kita melihat bagaimana keempat makna ini saling berhubungan satu sama lain?

Dalam diagram berikut, setiap subgraph mewakili salah satu dari 4 kemungkinan ini. Ilustrasi memvisualisasikan panjang rata-rata pesan. Mereka disusun dalam kotak, sehingga jika pesan berasal dari distribusi yang sama, bagan berada di dekatnya, dan jika mereka menggunakan kode yang sama, mereka berada di atas satu sama lain. Ini memungkinkan Anda untuk menggabungkan distribusi dan kode secara visual.



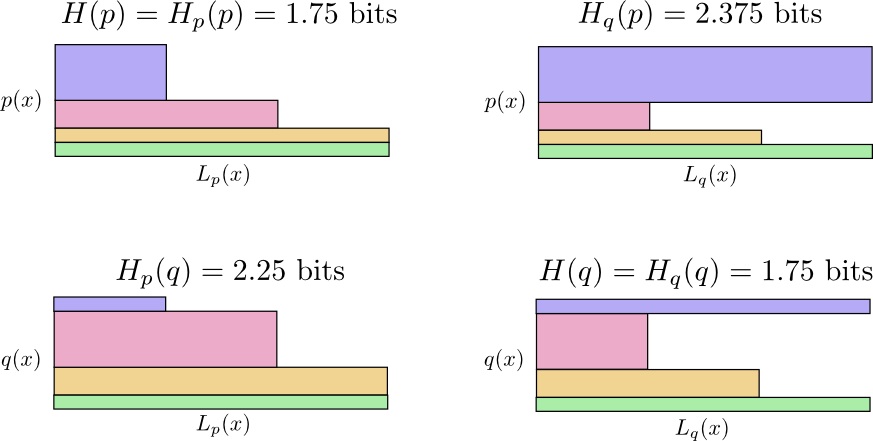
Lihat mengapa $$$H_p (q) ≠ H_q (p)$ ? $$$H_q (p)$ begitu besar, karena peristiwa yang ditandai dengan warna biru sering terjadi ketika $$$p$ tetapi mendapat codeword yang panjang karena sangat jarang $$$q$ . Di sisi lain, sering terjadi acara bersama $$$q$ kurang umum dengan $$$p$ tetapi karena itu perbedaannya tidak terlalu dramatis $$$H_p (q) Hp (q)$ sedikit kurang.

Entropi silang tidak simetris.

Jadi mengapa Anda harus peduli dengan entropi silang? Cross entropy memberi kita cara untuk menyatakan betapa berbedanya dua distribusi probabilitas itu. Semakin berbeda distribusinya $$$p$ dan $$$q$ semakin besar entropi silang $$$p$ tentang $$$q$ akan ada lebih banyak entropi $$$p$ .



Demikian pula lebih $$$q$ berbeda dari $$$p$ semakin besar entropi silang $$$q$ tentang $$$p$ akan ada lebih banyak entropi $$$q$ .

Yang sangat menarik adalah perbedaan antara entropi dan cross entropy. Perbedaan ini sama dengan berapa lama posting kami, karena kami menggunakan kode yang dioptimalkan untuk distribusi lain. Jika distribusinya sama, maka perbedaan ini akan menjadi nol. Dengan meningkatnya perbedaan, itu akan menjadi lebih besar.

Kami menyebutnya perbedaan Kullback-Leibler divergence, atau hanya KL divergence. Divergensi KL $$$p$ tentang $$$q$ , $$$D_q (p)$ didefinisikan sebagai berikut:

$$

$$D_q (p) = H_q (p) - H (p)$$

Hal yang hebat tentang divergensi KL adalah sepertinya jarak antara dua distribusi. Ini mengukur betapa berbedanya mereka! (Jika Anda menganggap serius ide ini, Anda akan datang ke geometri informasi.)

Cross entropy dan KL divergence sangat berguna dalam pembelajaran mesin. Seringkali kita ingin satu distribusi dekat dengan yang lain. Sebagai contoh, kita mungkin ingin distribusi yang diprediksi dekat dengan kebenaran yang mendasarinya. Divergensi KL memberi kita cara alami untuk melakukan ini, dan karena itu memanifestasikan dirinya di mana-mana.

Entropi dan beberapa variabel

Mari kita kembali ke contoh cuaca dan pakaian yang diberikan sebelumnya:




Ibu saya, seperti banyak orang tua, kadang-kadang khawatir bahwa saya tidak berpakaian sesuai cuaca. (Dia punya alasan kuat untuk dicurigai - kadang-kadang saya tidak memakai jas hujan di musim dingin). Karena itu, dia sering ingin tahu cuaca dan apa yang saya kenakan. Berapa banyak bit yang harus saya kirimkan untuk melaporkan ini?

Cara termudah untuk memikirkan ini adalah dengan meratakan distribusi probabilitas:



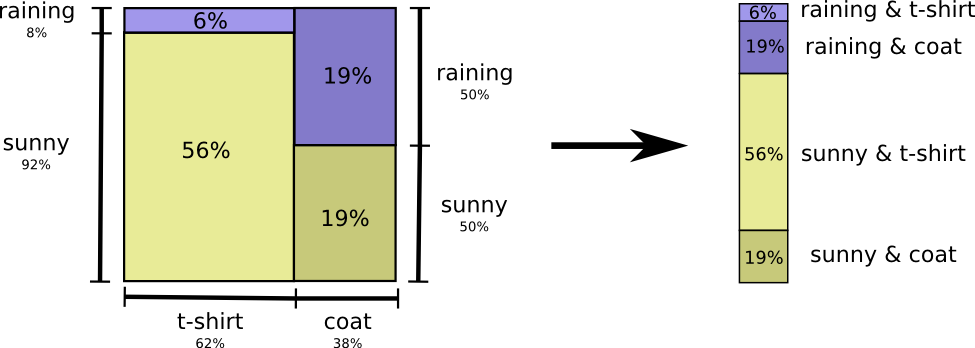
Sekarang kita dapat menghitung kata-kata kode optimal untuk acara dengan probabilitas seperti itu dan menghitung panjang pesan rata-rata:



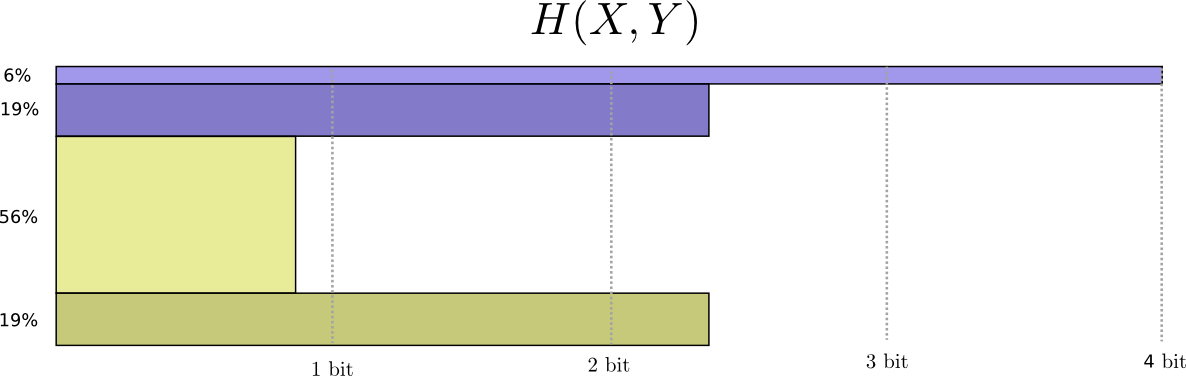
Kami menyebutnya entropi bersama $$$X$ dan $$$Y$ didefinisikan sebagai berikut:

$$

$$H (X, Y) = \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x, y)} \ bigg)$$

Itu bertepatan dengan definisi biasa kita, dengan pengecualian dua variabel, bukan satu.

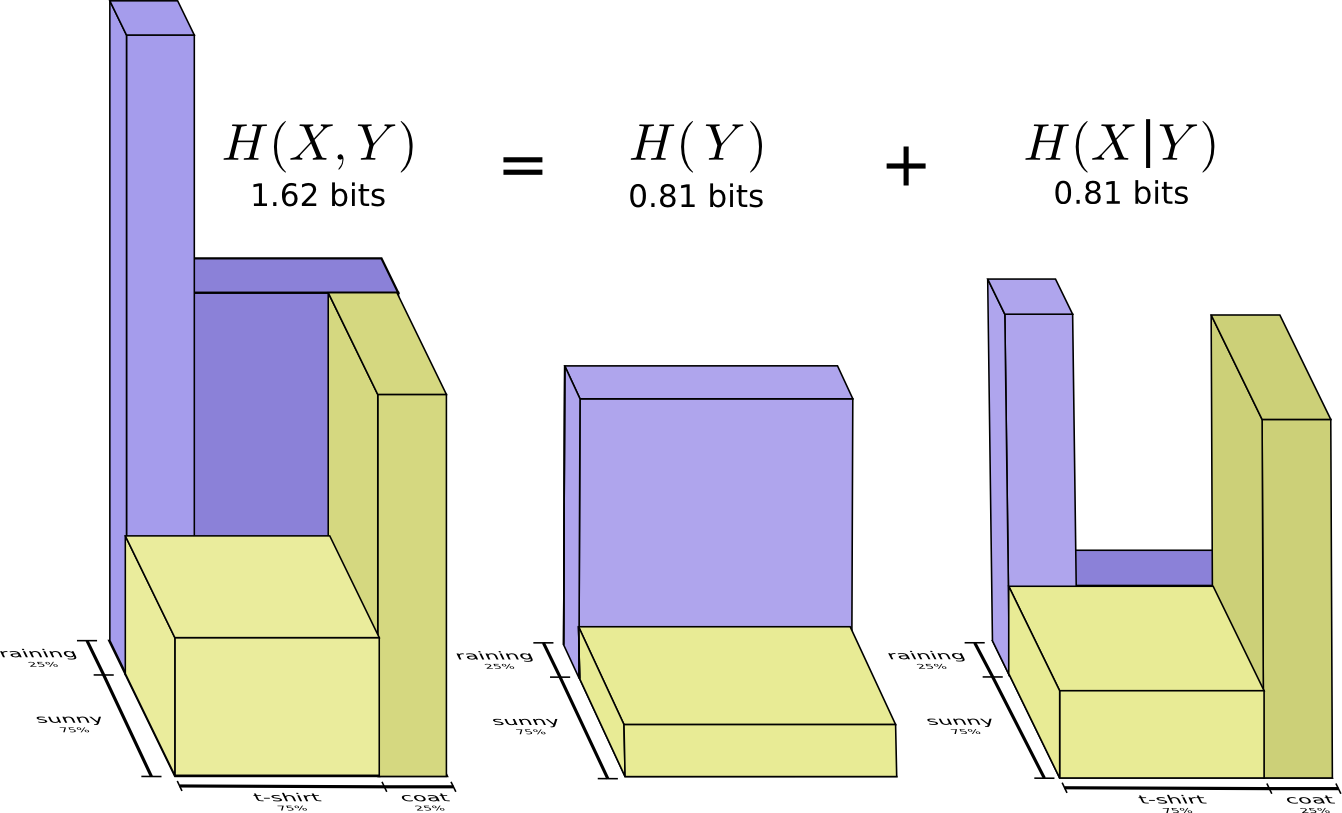
Gambar yang sedikit lebih baik dari ini, tanpa menyamakan distribusi, diperoleh dengan merepresentasikan panjang kata kode di dimensi ketiga. Sekarang entropi adalah volume!



Tapi misalkan ibuku sudah tahu cuacanya. Dia bisa melihatnya dalam berita. Berapa banyak informasi yang perlu saya berikan?

Sepertinya saya perlu mengirim informasi yang cukup untuk memberi tahu saya pakaian apa yang saya kenakan. Tetapi pada kenyataannya, saya perlu mengirimkan lebih sedikit informasi, karena cuaca apa yang akan saya pakai sangat bergantung pada cuaca! Mari kita lihat kasus hujan dan matahari secara terpisah.



Dalam kedua kasus, saya tidak perlu mengirim terlalu banyak informasi rata-rata, karena cuaca memberi saya tebakan yang baik tentang apa jawaban yang benar. Saat matahari, saya bisa menggunakan kode khusus yang dioptimalkan untuk matahari, dan saat hujan, saya bisa menggunakan kode yang dioptimalkan untuk hujan. Dalam kedua kasus, saya mengirim lebih sedikit informasi daripada jika saya menggunakan kode umum untuk keduanya. Untuk mendapatkan jumlah rata-rata informasi yang perlu saya kirimkan kepada ibu saya, saya hanya menggabungkan kedua kasus ini ...



Kami menyebutnya entropi bersyarat ini. Jika Anda memformalkannya ke dalam persamaan, Anda mendapatkan:

$$

$$H (X | Y) = \ sum_yp (y) \ sum_xp (x | y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

$$

$$= \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

Informasi timbal balik

Pada bagian sebelumnya, kami menemukan bahwa mengetahui satu variabel dapat berarti bahwa lebih sedikit informasi yang diperlukan untuk mengkomunikasikan nilai variabel lain.

Cara yang baik untuk memikirkannya adalah dengan membayangkan jumlah informasi dalam bentuk garis-garis. Pita-pita ini tumpang tindih jika ada informasi umum di antara mereka. Misalnya, beberapa informasi dalam $$$X$ dan $$$Y$ oleh karena itu umum $$$H (X)$ dan $$$H (Y)$ adalah garis-garis yang tumpang tindih. Dan sejak itu $$$H (X, Y)$ Apakah informasi kedua variabel, maka ini adalah penyatuan band $$$H (X)$ dan $$$H (Y)$ .



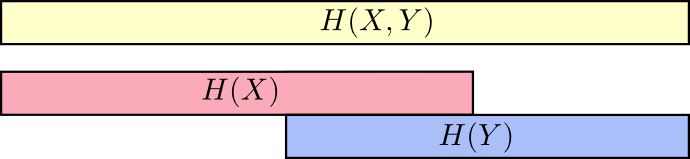
Ketika kita memikirkan hal-hal seperti ini, banyak yang menjadi lebih mudah dilihat.

Sebagai contoh, kami telah mencatat bahwa untuk mengirimkan informasi sebagai $$$X$ begitu dan $$$Y$ ("Entropi bersama", $$$H (X, Y)$ ) diperlukan lebih banyak informasi daripada hanya untuk transmisi $$$X$ ("Entropi Ultimate", $$$H (X)$ ) Tapi kalau sudah tahu $$$Y$ kemudian untuk transmisi $$$X$ ("Entropi bersyarat", $$$H (X | Y)$ ) lebih sedikit informasi yang diperlukan daripada jika Anda tidak tahu ini!



Kedengarannya rumit, tetapi jika Anda menerjemahkan ke dalam band maka semuanya ternyata sangat sederhana. $$$H (X | Y)$ Adalah informasi yang harus kami kirim untuk menginformasikan $$$X$ orang yang sudah tahu $$$Y$ informasi dalam $$$X$ yang juga tidak masuk $$$Y$ . Secara visual, ini artinya $$$H (X | Y)$ - ini adalah bagian dari strip $$$H (X)$ yang tidak tumpang tindih dengan $$$H (Y)$ .

Sekarang Anda bisa membaca ketidaksetaraan $$$H (X, Y) ≥H (X) ≥H (X | Y)$ tepat di grafik berikutnya.



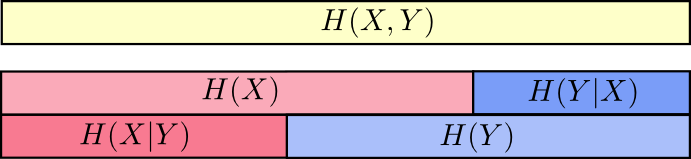
Kesetaraan lain adalah sebagai berikut - $$$H (X, Y) = H (Y) + H (X | Y)$ . Yaitu informasi dalam $$$X$ dan $$$Y$ ini adalah informasi dalam $$$Y$ ditambah informasi dalam $$$X$ yang tidak ada di $$$Y$ .



Sekali lagi, ini sulit dilihat dalam persamaan, tetapi mudah untuk melihat apakah Anda berpikir dalam hal tumpang tindih kumpulan informasi.

Pada titik ini, kami memecah informasi menjadi $$$X$ dan $$$Y$ dalam beberapa cara. Kami tahu informasi di setiap variabel, $$$H (X)$ dan $$$H (Y)$ . Kami tahu kombinasi informasi di keduanya $$$H (X, Y)$ . Kami memiliki informasi yang ada di satu variabel tetapi tidak di yang lain, $$$H (X | Y)$ dan $$$H (Y | X)$ . Sebagian besar dari ini berputar di sekitar informasi umum untuk variabel - persimpangan informasi mereka. Kami menyebutnya "informasi timbal balik," $$$I (x, y)$ didefinisikan sebagai:

$$

$$I (X, Y) = H (X) + H (Y) −H (X, Y)$$

Definisi ini benar karena $$$H (X) + H (Y)$ berisi dua salinan informasi timbal balik, karena juga terletak di $$$X$ dan masuk $$$Y$ sementara $$$H (X, Y)$ hanya mengandung satu salinan. (lihat diagram sebelumnya)

Variasi informasi terkait erat dengan informasi timbal balik. Variasi informasi adalah informasi yang tidak umum untuk variabel. Kita dapat mendefinisikannya seperti ini:

$$

$$V (X, Y) = H (X, Y) −I (X, Y)$$

Variasi informasi menarik karena memberi kita metrik, konsep jarak antara variabel yang berbeda. Variasi informasi antara dua variabel adalah nol jika mengetahui nilai dari satu variabel memberi tahu Anda makna yang lain dan menjadi lebih besar karena mereka menjadi lebih mandiri.

Bagaimana ini berhubungan dengan KL divergensi, yang juga memberi kita konsep jarak? Divergensi KL adalah jarak antara dua distribusi pada variabel yang sama atau serangkaian variabel. Sebaliknya, variasi informasi memberi kita jarak antara dua variabel yang didistribusikan bersama. Divergensi KL adalah perbedaan antara distribusi, variasi informasi dalam distribusi.

Kita dapat menggabungkan semuanya menjadi satu diagram yang menghubungkan semua jenis informasi yang berbeda ini:

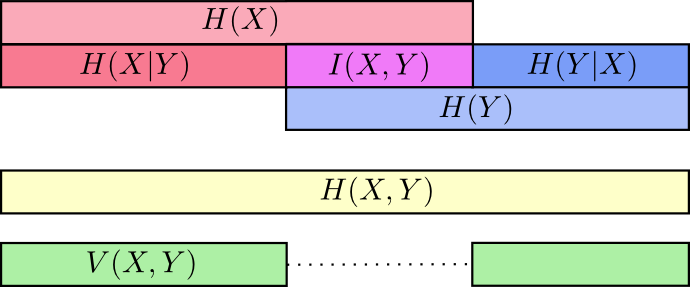
Bit pecahan

Suatu hal yang sangat tidak intuitif dalam teori informasi adalah bahwa kita dapat memiliki jumlah fraksi bit. Ini sangat aneh. Apa artinya setengah sedikit?

Inilah jawaban sederhana: sering kali kita tertarik pada panjang pesan rata-rata, daripada panjang pesan tertentu. Jika dalam setengah kasus satu bit dikirim, dan dalam setengah kasus dua, maka rata-rata satu setengah bit dikirim. Tidak ada yang aneh dalam kenyataan bahwa rata-rata dapat bersifat pecahan.

Tetapi dengan jawaban ini kita menghindar dari pertanyaan. Seringkali panjang kode kata yang optimal juga fraksional. Apa artinya ini?

Untuk lebih spesifik, mari kita lihat distribusi probabilitas, di mana satu peristiwa, $$$a$ terjadi 71% dari waktu, dan acara lain, $$$b$ terjadi 29% dari waktu.



Kode optimal akan menggunakan 0,5 bit untuk mewakili $$$a$ dan 1,7 bit untuk diwakili $$$b$ . Nah, jika kita hanya ingin mengirim salah satu dari kata-kata kode ini, representasi seperti itu tidak mungkin. Kami dipaksa untuk membulatkan jumlah integer bit dan mengirim rata-rata 1 bit.

... Tetapi jika kami mengirim beberapa pesan sekaligus, maka ternyata kami bisa melakukan yang lebih baik. Mari kita perhatikan transmisi dua peristiwa dari distribusi ini. Jika kami mengirimnya secara independen, kami harus mengirim dua bit. Bagaimana kita meningkatkan ini?



Dalam setengah kasus, kami perlu mengirim $$$aa$ , dalam 21% kasus - $$$ab$ atau $$$ba$ , dan dalam 8% kasus - $$$bb$ . Sekali lagi, kode yang ideal termasuk bit fraksional.



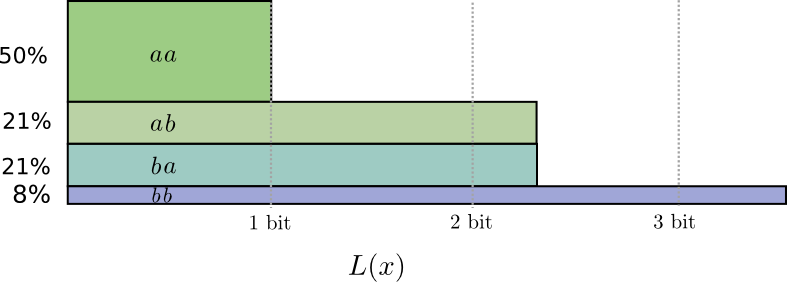
Jika kita melengkapi panjang kata sandi, kita mendapatkan sesuatu seperti ini:



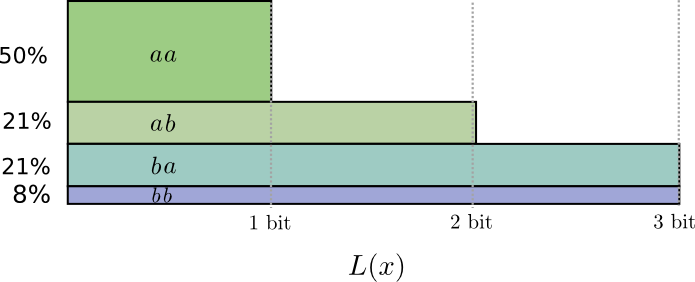
Kode-kode ini memberi kami panjang pesan rata-rata 1,8 bit. Ini kurang dari 2 bit ketika kami mengirim pesan secara mandiri. Yaitu dalam hal ini, kami mengirim 0,9 bit rata-rata untuk setiap acara. Jika kami mengirim lebih banyak acara sekaligus, rata-rata akan lebih sedikit. Di $$$n$ cenderung hingga tak terbatas, overhead yang terkait dengan pembulatan kode kita akan hilang, dan jumlah bit per codeword akan konvergen menjadi entropi.

Selanjutnya, perhatikan bahwa panjang kata sandi ideal untuk acara tersebut $$$a$ adalah 0,5 bit, dan panjang ideal untuk codeword $$$aa$ - 1 bit. Panjang codeword ideal bertambah, bahkan jika itu pecahan! Jadi, jika kami melaporkan beberapa acara sekaligus, panjangnya akan bertambah.

Seperti yang dapat kita lihat, ada arti sebenarnya untuk sejumlah kecil bit informasi, bahkan jika kode sebenarnya hanya dapat menggunakan bilangan bulat.

(Dalam praktiknya, orang menggunakan skema pengkodean tertentu yang efektif dalam kasus yang berbeda. Kode Huffman, yang sebenarnya merupakan jenis kode yang kami buat di sini, tidak menangani bit fraksional dengan sangat elegan - Anda harus mengelompokkan karakter seperti yang kami lakukan di atas, atau menggunakan trik yang lebih kompleks untuk mendekati batas entropi. Pengodean aritmatika sedikit berbeda, ia secara elegan memproses bit fraksional menjadi optimal asimtotik.)

Kesimpulan

Jika kita khawatir tentang transfer informasi untuk jumlah bit minimum, maka ide-ide ini, tentu saja, mendasar. Jika kita peduli tentang kompresi data, teori informasi memecahkan masalah utama dan memberi kita abstraksi yang benar secara fundamental. Tetapi bagaimana jika kita tidak peduli - bukankah itu eksotis?

Gagasan dari teori informasi muncul dalam banyak konteks: pembelajaran mesin, fisika kuantum, genetika, termodinamika, dan bahkan perjudian. Praktisi di bidang ini tidak peduli dengan teori informasi karena mereka ingin mengompres informasi. Mereka peduli bahwa itu memiliki hubungan yang tak tertahankan dengan daerah mereka. Keterikatan kuantum dapat digambarkan dengan entropi. Banyak hasil dalam mekanika statistik dan termodinamika dapat diperoleh dengan mengasumsikan entropi maksimum tentang hal-hal yang tidak Anda ketahui. Keuntungan dan kerugian pemain secara langsung terkait dengan perbedaan KL, khususnya, pengaturan yang diulang.

Teori informasi muncul di semua tempat ini karena menawarkan formalisasi yang konkret dan mendasar untuk banyak hal yang harus kita ungkapkan. Ini memberi kita cara untuk mengukur dan mengekspresikan ketidakpastian, betapa berbedanya dua set keyakinan itu, dan bahwa jawaban untuk satu pertanyaan memberi tahu kita tentang yang lain: seberapa tersebar probabilitas, jarak antara distribusi probabilitas, dan seberapa tergantung dua variabel. Apakah ada alternatif, ide serupa? Tentu saja Tetapi ide-ide dari teori informasi murni, mereka memiliki sifat yang sangat bagus dan didasarkan pada prinsip-prinsip. Dalam beberapa kasus, ide-ide ini persis apa yang Anda butuhkan, dan dalam kasus lain, mereka adalah mediator yang nyaman di dunia yang kacau.

Pembelajaran mesin adalah yang saya tahu terbaik, jadi mari kita bicarakan satu menit. Jenis tugas yang sangat umum dalam pembelajaran mesin adalah klasifikasi. Misalkan kita ingin melihat gambar dan memprediksi apakah itu akan menjadi gambar anjing atau kucing. Model kami mungkin mengatakan sesuatu seperti: "Ada kemungkinan 80% bahwa ini adalah gambar seekor anjing, dan probabilitas 20% bahwa itu adalah kucing." Apa itu anjing 80%? Seberapa baik mengatakan 85%?

Ini adalah pertanyaan penting karena kita perlu beberapa gagasan tentang seberapa baik atau buruk model kita untuk mengoptimalkannya agar berhasil. Apa yang harus kita optimalkan? Jawaban yang benar sebenarnya tergantung pada apa yang kita gunakan untuk model: apakah kita hanya peduli apakah tebakan kita benar, atau kita peduli seberapa yakin kita pada jawaban yang benar?Seberapa buruk kesalahannya dengan percaya diri? Tidak ada jawaban yang benar untuk ini. Dan seringkali tidak mungkin untuk menemukan jawaban yang benar, karena kita tidak tahu persis bagaimana model akan digunakan untuk memformalkan apa yang akhirnya membuat kita bersemangat. Ada situasi ketika cross entropy adalah hal yang membuat kita khawatir, tetapi hal ini tidak selalu terjadi. Lebih sering, kita tidak tahu persis apa yang membuat kita khawatir, dan lintas-entropi adalah proxy yang sangat bagus.

Informasi memberi kita dasar baru yang kuat untuk berpikir tentang dunia. Terkadang ini ideal untuk tugas yang diberikan; dalam kasus lain, tidak cukup, tetapi masih sangat bermanfaat. Esai ini hanya menggores permukaan teori informasi - ada topik dasar, seperti kode koreksi kesalahan, yang tidak kami sentuh sama sekali, tetapi saya harap saya telah menunjukkan bahwa teori informasi adalah subjek yang luar biasa yang tidak boleh diintimidasi.