Mengapa pemilahan cepat sangat lambat? Metode Urutan Array Baru

Banyak programmer berpikir bahwa Sort Cepat adalah algoritma tercepat dari semua. Ini sebagian benar. Tapi itu bekerja sangat baik hanya jika elemen pendukung dipilih dengan benar ( maka kompleksitasnya adalah O (n log n) ). Jika tidak, perilaku asimptotik akan kira-kira sama dengan perilaku gelembung ( mis., O (n ² ) ).
Pada saat yang sama, jika array sudah diurutkan, maka algoritma akan tetap bekerja tidak lebih cepat dari O (n log n)

Berdasarkan ini, saya memutuskan untuk menulis algoritma saya sendiri untuk mengurutkan array yang akan bekerja lebih baik daripada quick_sort. Dan jika array sudah diurutkan, maka jangan jalankan beberapa kali, seperti halnya dengan banyak algoritma.

“Saat itu malam, tidak ada yang bisa dilakukan,” - Sergei Mikhalkov.

Persyaratan:

1. Kasus terbaik O (n)
2. Kasus rata-rata O (n log n)
3. Kasus terburuk O (n log n)
4. Rata-rata lebih cepat daripada penyortiran cepat

Sekarang mari kita selesaikan semuanya

Agar algoritma kami selalu bekerja dengan cepat, perlu bahwa dalam kasus rata-rata perilaku asimptotik setidaknya O (n log n), dan paling baik, O (n). Kita semua tahu betul bahwa, paling banter, penyortiran penyisipan berfungsi sekaligus. Tetapi paling buruk, dia harus berkeliling array sebanyak yang ada elemen di dalamnya.

Informasi awal

int* glue(int* a, int lenA, int* b, int lenB) { int lenC = lenA + lenB; int* c = new int[lenC]; //   int indx_a = 0; int indx_b = 0; int i = 0; for (; i < lenC; ++i) { if (indx_a < lenA) { if (indx_b < lenB) { //     c[i] = (a[indx_a] < b[indx_b]) ? a[indx_a++] : b[indx_b++]; continue; } //      while (indx_a < lenA) c[i++] = a[indx_a++]; } else //      while (indx_b < lenB) c[i++] = b[indx_b++]; break; } return c; } 

 void glueDelete(int*& arr, int*& a, int lenA, int*& b, int lenB) { if (lenA == 0) { //    delete[] a; //     arr = b; //     return; } if (lenB == 0) { //    delete[] b; //     arr = a; //     return; } int *copy = glue(a, lenA, b, lenB); //  delete[]a; //    delete[]b; //    arr = copy; //   } 

 void insertionSort(int*& arr, int lo, int hi) { for (int i = lo + 1; i <= hi; ++i) for (int j = i; j > 0 && arr[j - 1] > arr[j]; --j) swap(arr[j - 1], arr[j]); } 

Versi awal algoritma (tidak optimal):

Ide utama dari algoritma ini adalah apa yang disebut pencarian maksimum (dan minimum). Pada setiap iterasi, pilih elemen dari array. Jika lebih besar dari maksimum sebelumnya, kemudian tambahkan elemen ini ke akhir seleksi. Jika tidak, jika kurang dari minimum sebelumnya, maka kami menambahkan elemen ini ke awal. Jika tidak, letakkan di array yang terpisah.

Fungsi input mengambil array dan jumlah elemen dalam array ini

 void FirstNewGeneratingSort(int*& arr, int len) 

Untuk menyimpan sampel dari array (tertinggi dan terendah) dan elemen lainnya, kami mengalokasikan memori

 int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       int* restElements = new int[len]; //  ,      int restLen = 0; //      

Seperti yang Anda lihat, kami mengalokasikan 2 kali lebih banyak memori untuk menyimpan sampel daripada array asli kami. Ini dilakukan jika kita memiliki array yang diurutkan dan setiap elemen berikutnya akan menjadi maksimum baru. Maka hanya bagian kedua dari array sampel yang akan ditempati. Atau sebaliknya (jika diurutkan dalam urutan menurun).

Untuk sampel, pertama Anda perlu minimum awal dan maksimum. Cukup pilih elemen pertama dan kedua

 if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1]; 

Sampling sendiri

 for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i]) //     { selection[right++] = arr[i]; continue; } if (selection[left + 1] >= arr[i]) //     { selection[left--] = arr[i]; continue; } restElements[restLen++] = arr[i]; //      ,    } 

Sekarang kita memiliki serangkaian elemen yang diurutkan, dan elemen "tersisa" yang masih harus kita sortir. Tetapi pertama-tama Anda perlu melakukan manipulasi memori.

Kosongkan memori yang tidak digunakan

 int selectionLen = right - left - 1; //   int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //       delete[] selection; //   2 * len ,         ,     selection = copy; //  ,    selection     delete[] arr; //    ,         ,       

Buat panggilan sortir rekursif untuk elemen yang tersisa dan gabungkan dengan pilihan

 FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen); 

 void FirstNewGeneratingSort(int*& arr, int len) { if (len < 2) return; int* selection = new int[len << 1]; int left = len - 1; int right = len; int* restElements = new int[len]; int restLen = 0; if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1]; for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i]) //     { selection[right++] = arr[i]; continue; } if (selection[left + 1] >= arr[i]) //     { selection[left--] = arr[i]; continue; } restElements[restLen++] = arr[i]; //      ,    } int selectionLen = right - left - 1; //   int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //       delete[] selection; //   2 * len ,          ,     selection = copy; //  ,    selection     delete[] arr; //    ,         ,       FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen); } 

Mari kita periksa kecepatan algoritma dibandingkan dengan Sort Cepat

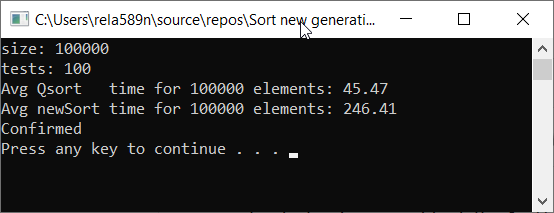
Seperti yang Anda lihat, ini sama sekali bukan yang kami inginkan. Hampir 6 kali lebih lama dari QuickSort! Tetapi waktu dalam konteks ini tidak tepat untuk digunakan, karena di sini asimptotik yang penting. Dalam implementasi algoritma ini, dalam kasus terburuk, elemen pertama dan kedua akan menjadi minimum dan maksimum. Dan sisanya akan disalin ke array yang terpisah.

Kompleksitas Algoritma:

• Kasus terburuk: O (n ² )
• Kasus tengah: O (n ² )
• Kasus terbaik: O (n)

Hmm, ini tidak lebih baik dari penyortiran yang sama dengan memasukkan. Ya, memang kita dapat menemukan elemen (minimum) maksimum dengan sangat cepat, dan sisanya tidak akan masuk ke dalam seleksi.

Kami dapat mencoba untuk mengoptimalkan semacam penggabungan. Pertama, periksa kecepatan semacam penggabungan:

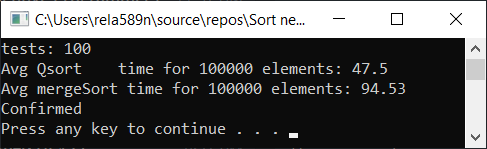
 void newGenerationMergeSort(int* a, int lo, int hi, int& minPortion) { if (hi <= lo) return; int mid = lo + (hi - lo) / 2; if (hi - lo <= minPortion) { //       ,     int* part = glue(a + lo, hi - lo + 1, nullptr, 0); //    FirstNewGeneratingSort(part, hi - lo + 1); for (int i = lo; i <= hi; ++i) { a[i] = part[i - lo]; } delete[] part; return; } newGenerationMergeSort(a, lo, mid, minPortion); newGenerationMergeSort(a, mid + 1, hi, minPortion); int* b = glue(a + lo, mid - lo + 1, a + mid + 1, hi - mid); for (int i = lo; i <= hi; i++) a[i] = b[i - lo]; delete[] b; } 

Beberapa jenis pembungkus dibutuhkan untuk kemudahan penggunaan.

 void newMergeSort(int *arr, int length) { int portion = log2(length); //      portion *= portion; newGenerationMergeSort(arr, 0, length - 1, portion); } 

Hasil tes:

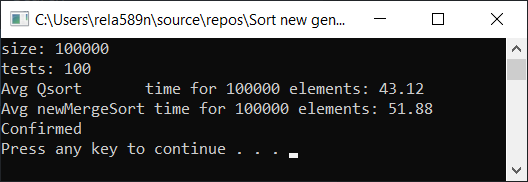
Ya, peningkatan kecepatan diamati, tetapi meskipun demikian, fungsi ini tidak berfungsi secepat Sort Cepat. Selain itu, kami tidak dapat berbicara tentang O (n) pada array yang diurutkan. Oleh karena itu, opsi ini juga dibuang.

Opsi pengoptimalan untuk opsi pertama

1. Agar kompleksitas tidak menjadi O (n ² ), kita dapat menambahkan elemen yang tidak termasuk dalam sampel tidak dalam 1 array seperti sebelumnya, tetapi memperluasnya menjadi 2 array. Setelah itu, tinggal menyortir kedua bagian ini, dan menggabungkannya dengan sampel kami. Akibatnya, kami mendapatkan kompleksitas sama dengan O (n log n)

2. Seperti yang telah kita perhatikan, elemen absolut (minimum) dalam array yang diurutkan dapat ditemukan dengan cepat, dan ini tidak terlalu efektif. Di sinilah penyortiran penyisipan masuk untuk membantu kami. Pada setiap iterasi seleksi, kami akan memeriksa apakah kami dapat memasukkan elemen aliran ke dalam satu set yang terakhir, misalnya, delapan dimasukkan.

Jika tidak jelas sekarang, jangan kecewa. Seharusnya begitu. Sekarang semuanya akan menjadi jelas pada kode dan pertanyaan akan hilang.

Versi algoritma yang benar yang tersisa:

Tanda tangannya sama dengan di versi sebelumnya

 void newGenerationSort(int*& arr, int len) 

Tetapi harus dicatat bahwa opsi ini mengasumsikan pointer ke parameter pertama yang dapat dipanggil operasi delete [] (mengapa - kita akan lihat nanti). Yaitu, ketika kami mengalokasikan memori, kami menetapkan alamat awal array untuk pointer ini.

Persiapan awal

Dalam contoh ini, apa yang disebut "koefisien mengejar" hanyalah sebuah konstanta dengan nilai 8. Ini menunjukkan berapa banyak elemen maksimum yang kita coba lalui untuk memasukkan "di bawah maksimum" atau "di bawah minimum" yang baru sebagai gantinya.

 int localCatchUp = min(catchUp, len); //            insertionSort(arr, 0, localCatchUp - 1); //     localCatchUp  if (len <= localCatchUp) //       n <= catchUp ,   return; //    (      ) 

Untuk menyimpan sampel, buat sebuah array

Jika ada sesuatu yang tidak jelas, maka lihat penjelasan di versi awal

 int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       

Isi beberapa elemen pertama dari array pilihan

 selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { selection[right++] = arr[i]; } 

Biarkan saya mengingatkan Anda bahwa posisi terendah baru pergi ke sisi kiri tengah array sampel, dan tertinggi baru pergi ke kanan

Buat array untuk menyimpan item yang tidak dipilih

 int restLen = len >> 1; //     len / 2 int* restFirst = new int[restLen]; int* restSecond = new int[restLen]; int restFirstLen = 0; int restSecondLen = 0; 

Sekarang, hal yang paling penting adalah pemilihan elemen yang benar dari array sumber

Siklus dimulai dengan localCatchUp (karena elemen sebelumnya telah memasukkan sampel kami sebagai nilai dari mana kami akan mulai). Dan itu berlanjut sampai akhir. Jadi setelah, pada akhirnya, semua elemen akan didistribusikan baik ke dalam array pemilihan atau ke dalam salah satu array pilihan-bawah.

Untuk memeriksa apakah kita dapat memasukkan elemen ke dalam seleksi, kita hanya akan memeriksa apakah elemen tersebut lebih (atau sama) dengan posisi elemen 8 di sebelah kiri (kanan - localCatchUp). Jika demikian, maka kita cukup memasukkannya ke posisi yang diinginkan dengan satu kali melewati elemen-elemen ini. Ini untuk sisi kanan, yaitu untuk elemen maksimum. Dengan cara yang sama, kami melakukan yang sebaliknya untuk yang minimal. Jika Anda tidak dapat memasukkannya di kedua sisi pilihan, maka kami membuangnya ke salah satu array lainnya.

Loop akan terlihat seperti ini:

 for (int i = localCatchUp; i < len; ++i) { if (selection[right - localCatchUp] <= arr[i]) { selection[right] = arr[i]; for (int j = right; selection[j - 1] > selection[j]; --j) swap(selection[j - 1], selection[j]); ++right; continue; } if (selection[left + localCatchUp] >= arr[i]) { selection[left] = arr[i]; for (int j = left; selection[j] > selection[j + 1]; ++j) swap(selection[j], selection[j + 1]); --left; continue; } if (i & 1) { // i -  restFirst[restFirstLen++] = arr[i]; } else { restSecond[restSecondLen++] = arr[i]; } } 

Lagi-lagi, apa yang terjadi di sini? Pertama kita mencoba untuk mendorong elemen ke posisi tertinggi. Tidak berhasil? - Jika memungkinkan, lemparkan ke posisi terendah. Jika tidak mungkin melakukan ini juga - letakkan di restFirst atau restSecond.

Bagian tersulit sudah berakhir. Sekarang, setelah loop, kami memiliki array yang diurutkan dengan pilihan (elemen mulai di indeks [kiri + 1] dan berakhir di [kanan - 1] ), serta restFirst dan rest. Array kedua dari length restFirstLen dan restSecondLen, masing-masing.

Seperti pada contoh sebelumnya, sebelum panggilan rekursif kami membebaskan memori dari array utama (kami sudah menyimpan semua elemennya)

 delete[] arr; 

Array pilihan kami dapat berisi banyak sel memori yang tidak digunakan. Sebelum panggilan rekursif, Anda harus membebaskannya.

Kosongkan memori yang tidak digunakan

 int selectionLen = right - left - 1; //     int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //        delete[] selection; //    2 * len   selection = copy; //      ,   

Sekarang jalankan fungsi sortir kami secara rekursif untuk array restFirst dan restSecond

Untuk memahami cara kerjanya, pertama-tama Anda harus melihat kode sampai akhir. Untuk saat ini, Anda hanya perlu percaya bahwa setelah panggilan berulang, array restFirst dan restSecond akan diurutkan.

 newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen); 

Dan akhirnya, kita perlu menggabungkan 3 array ke dalam yang dihasilkan dan menetapkannya ke pointer pointer.

Pertama-tama Anda bisa menggabungkan restFirst + restSecond ke beberapa array restFull , dan kemudian menggabungkan seleksi + restFull . Tetapi algoritma ini memiliki sifat sedemikian rupa sehingga kemungkinan besar array seleksi akan mengandung elemen yang jauh lebih sedikit daripada array lainnya. Misalkan pilihan berisi 100 elemen, restFirst berisi 990, dan restSecond berisi 1010. Kemudian, untuk membuat array restFull , Anda perlu melakukan 990 + 1010 = 2000 operasi penyalinan. Kemudian untuk penggabungan dengan seleksi - 2000 + 100 salinan lainnya. Total dengan pendekatan ini, salinan total akan menjadi 2000 + 2100 = 4100.

Mari kita terapkan optimasi di sini. Pertama menggabungkan seleksi dan restFirst ke dalam array pemilihan . Menyalin operasi: 100 + 990 = 1090. Selanjutnya, gabungkan pilihan dan sisanya array Kedua dan menghabiskan 1090 + 1010 = 2100 salinan lainnya. Secara total, 2100 + 1090 = 3190 akan dirilis, yang hampir seperempat lebih sedikit dibandingkan dengan pendekatan sebelumnya.

Gabungan terakhir dari array

 int* part2; int part2Len; if (selectionLen < restFirstLen) { glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst selectionLen += restFirstLen; part2 = restSecond; part2Len = restSecondLen; } else { glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond part2Len = restFirstLen + restSecondLen; } glueDelete(arr, selection, selectionLen, part2, part2Len); 

Seperti yang Anda lihat, jika lebih menguntungkan bagi kita untuk menggabungkan seleksi dengan restFirst , maka kita melakukannya. Jika tidak, kami bergabung seperti dalam "restFull"

 /// works only if arr is pointer assigned by new keyword void newGenerationSort(int*& arr, int len) { int localCatchUp = min(catchUp, len); //            insertionSort(arr, 0, localCatchUp - 1); //     localCatchUp  if (len <= localCatchUp) //       n <= catchUp  return; //      int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { selection[right++] = arr[i]; } int restLen = len >> 1; int* restFirst = new int[restLen]; int* restSecond = new int[restLen]; int restFirstLen = 0; int restSecondLen = 0; for (int i = localCatchUp; i < len; ++i) { if (selection[right - localCatchUp] <= arr[i]) { selection[right] = arr[i]; for (int j = right; selection[j - 1] > selection[j]; --j) swap(selection[j - 1], selection[j]); ++right; continue; } if (selection[left + localCatchUp] >= arr[i]) { selection[left] = arr[i]; for (int j = left; selection[j] >= selection[j + 1]; ++j) swap(selection[j], selection[j + 1]); --left; continue; } if (i & 1) { // i -  restFirst[restFirstLen++] = arr[i]; } else { restSecond[restSecondLen++] = arr[i]; } } delete[] arr; int selectionLen = right - left - 1; //     int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //        delete[] selection; //    2 * len   selection = copy; //      ,   newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen); int* part2; int part2Len; if (selectionLen < restFirstLen) { glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst selectionLen += restFirstLen; part2 = restSecond; part2Len = restSecondLen; } else { glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond part2Len = restFirstLen + restSecondLen; } glueDelete(arr, selection, selectionLen, part2, part2Len); } 

Sekarang waktu pengujian

 #include <iostream> #include <ctime> #include <vector> #include <algorithm> #include "time_utilities.h" #include "sort_utilities.h" using namespace std; using namespace rela589n; void printArr(int* arr, int len) { for (int i = 0; i < len; ++i) { cout << arr[i] << " "; } cout << endl; } bool arraysEqual(int* arr1, int* arr2, int len) { for (int i = 0; i < len; ++i) { if (arr1[i] != arr2[i]) { return false; } } return true; } int* createArray(int length) { int* a1 = new int[length]; for (int i = 0; i < length; i++) { a1[i] = rand(); //a1[i] = (i + 1) % (length / 4); } return a1; } int* array_copy(int* arr, int length) { int* a2 = new int[length]; for (int i = 0; i < length; i++) { a2[i] = arr[i]; } return a2; } void tester(int tests, int length) { double t1, t2; int** arrays1 = new int* [tests]; int** arrays2 = new int* [tests]; for (int t = 0; t < tests; ++t) { //    int* arr1 = createArray(length); arrays1[t] = arr1; arrays2[t] = array_copy(arr1, length); } t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { quickSort(arrays1[t], 0, length - 1); } t2 = getCPUTime(); cout << "Avg Qsort time for " << length << " elements: " << (t2 - t1) * 1000 / tests << endl; int portion = catchUp = 8; t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { newGenerationSort(arrays2[t], length); } t2 = getCPUTime(); cout << "Avg newGenSort time for " << length << " elements: " << (t2 - t1) * 1000 / tests //<< " Catch up coef: "<< portion << endl; bool confirmed = true; //     for (int t = 0; t < tests; ++t) { if (!arraysEqual(arrays1[t], arrays2[t], length)) { confirmed = false; break; } } if (confirmed) { cout << "Confirmed" << endl; } else { cout << "Review your code! Something wrong..." << endl; } } int main() { srand(time(NULL)); int length; double t1, t2; cout << "size: "; cin >> length; int t; cout << "tests: "; cin >> t; tester(t, length); system("pause"); return 0; } 

 // [min, max] int random(int min, int max) { return min + rand() % ((max + 1) - min); } void quickSort(int * arr, int b, int e) { int l = b, r = e; int piv = arr[random(l, r)]; while (l <= r) { for (; arr[l] < piv; ++l); for (; arr[r] > piv; --r); if (l <= r) swap(arr[l++], arr[r--]); } if (b < r) quickSort(arr, b, r); if (e > l) quickSort(arr, l, e); } 

 #pragma once #if defined(_WIN32) #include <Windows.h> #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) #include <unistd.h> #include <sys/resource.h> #include <sys/times.h> #include <time.h> #else #error "Unable to define getCPUTime( ) for an unknown OS." #endif /** * Returns the amount of CPU time used by the current process, * in seconds, or -1.0 if an error occurred. */ double getCPUTime() { #if defined(_WIN32) /* Windows -------------------------------------------------- */ FILETIME createTime; FILETIME exitTime; FILETIME kernelTime; FILETIME userTime; if (GetProcessTimes(GetCurrentProcess(), &create;Time, &exit;Time, &kernel;Time, &user;Time) != -1) { SYSTEMTIME userSystemTime; if (FileTimeToSystemTime(&user;Time, &user;SystemTime) != -1) return (double)userSystemTime.wHour * 3600.0 + (double)userSystemTime.wMinute * 60.0 + (double)userSystemTime.wSecond + (double)userSystemTime.wMilliseconds / 1000.0; } #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) /* AIX, BSD, Cygwin, HP-UX, Linux, OSX, and Solaris --------- */ #if defined(_POSIX_TIMERS) && (_POSIX_TIMERS > 0) /* Prefer high-res POSIX timers, when available. */ { clockid_t id; struct timespec ts; #if _POSIX_CPUTIME > 0 /* Clock ids vary by OS. Query the id, if possible. */ if (clock_getcpuclockid(0, &id;) == -1) #endif #if defined(CLOCK_PROCESS_CPUTIME_ID) /* Use known clock id for AIX, Linux, or Solaris. */ id = CLOCK_PROCESS_CPUTIME_ID; #elif defined(CLOCK_VIRTUAL) /* Use known clock id for BSD or HP-UX. */ id = CLOCK_VIRTUAL; #else id = (clockid_t)-1; #endif if (id != (clockid_t)-1 && clock_gettime(id, &ts;) != -1) return (double)ts.tv_sec + (double)ts.tv_nsec / 1000000000.0; } #endif #if defined(RUSAGE_SELF) { struct rusage rusage; if (getrusage(RUSAGE_SELF, &rusage;) != -1) return (double)rusage.ru_utime.tv_sec + (double)rusage.ru_utime.tv_usec / 1000000.0; } #endif #if defined(_SC_CLK_TCK) { const double ticks = (double)sysconf(_SC_CLK_TCK); struct tms tms; if (times(&tms;) != (clock_t)-1) return (double)tms.tms_utime / ticks; } #endif #if defined(CLOCKS_PER_SEC) { clock_t cl = clock(); if (cl != (clock_t)-1) return (double)cl / (double)CLOCKS_PER_SEC; } #endif #endif return -1; /* Failed. */ } 

Semua tes dilakukan pada mesin dengan persentase. Intel core i3 7100u dan 8GB RAM

Array yang sepenuhnya acak

 a1[i] = rand(); 

Array yang Dipesan Sebagian

 a1[i] = (i + 1) % (length / 4); 

Array Lengkap Diurutkan

 a1[i] = (i + 1); 

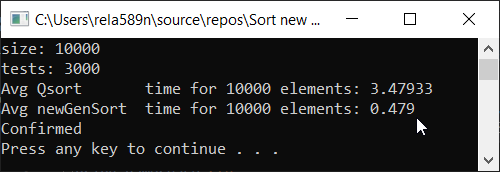
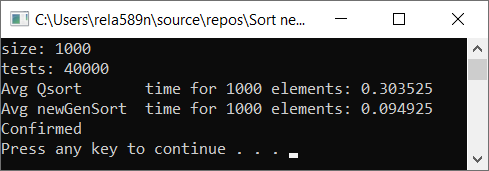
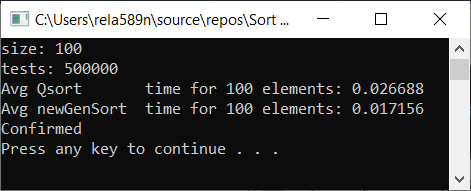
Kesimpulan

Seperti yang Anda lihat, algoritme bekerja dan bekerja dengan baik. Setidaknya semua yang kami inginkan tercapai. Dengan mengorbankan stabilitas, saya tidak yakin saya tidak memeriksa. Anda bisa memeriksanya sendiri. Tetapi secara teori itu harus dicapai dengan sangat mudah. Hanya di beberapa tempat, bukannya tanda>, taruh ≥ atau sesuatu.