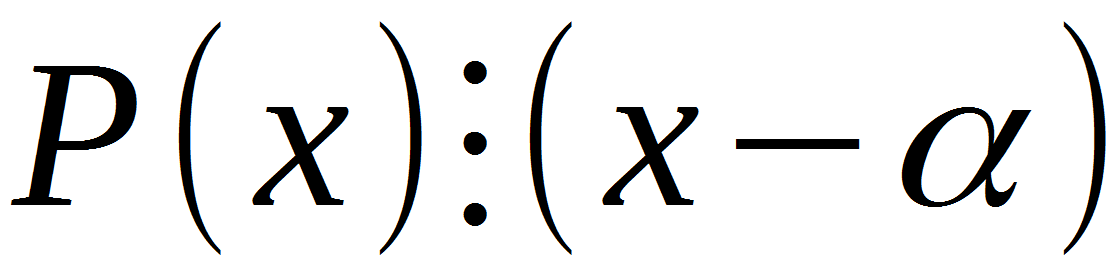
Sebagai aturan, dalam fisika, ilmu komputer, dan ekonomi, kita dihadapkan dengan persamaan linear sederhana, atau fraksional, lebih jarang dengan persamaan kuadratik. Dan bagaimana dengan persamaan tingkat ketiga dan keempat? Jika Anda tertarik, maka saya minta kucing.
Pertama, pertimbangkan konsep persamaan tingkat tertinggi. Persamaan tingkat tertinggi adalah persamaan bentuk:

Pada artikel ini saya akan mempertimbangkan:
1. Persamaan kubik.
2. Kubik dikembalikan.
3. Penerapan skema Horner dan teorema Bezout.
4. Persamaan biquadratic yang dapat dikembalikan.
Persamaan kubik
Persamaan kubik adalah persamaan di mana derajat tidak diketahui tidak diketahui untuk istilah senior. Persamaan kubik memiliki bentuk berikut:

Persamaan tersebut dapat diselesaikan dengan cara yang berbeda, namun, kami akan menggunakan pengetahuan sekolah dasar dan memecahkan persamaan kubik dengan metode pengelompokan:

Dalam contoh ini, metode pengelompokan digunakan, kami mengelompokkan dua anggota pertama dan dua terakhir, mendapatkan tanda kurung sama, sekali lagi kami melihat, mendapatkan persamaan dua tanda kurung.
Produk sama dengan nol, dan hanya jika setidaknya satu faktor sama dengan nol, atas dasar ini kami menyamakan setiap faktor (braket) dengan nol, memperoleh persamaan kuadratik dan linier yang tidak lengkap.
Perlu juga dicatat bahwa jumlah akar maksimum dari suatu persamaan sama dengan derajat yang tidak diketahui dengan istilah terkemuka, sehingga dalam persamaan kubik tidak boleh lebih dari tiga akar, dalam biquadratic (derajat 4) tidak lebih dari empat akar dan. dll.
Kembali Persamaan Kubik
Persamaan kubik pengembalian memiliki bentuk:

Mereka disebut dapat dikembalikan karena koefisien akan dicerminkan. Persamaan serupa juga diselesaikan dengan metode sekolah, tetapi sedikit lebih rumit:

Pertama, pengelompokan dilakukan, kemudian menggunakan rumus perkalian disingkat, kami menguraikan faktor yang dihasilkan. Sekali lagi kita mendapatkan 2 tanda kurung yang sama, “kita keluarkan mereka”. Kami mendapatkan dua faktor (kurung) dan menyelesaikannya sebagai dua persamaan yang berbeda.
Teorema Bezout dan skema Horner
Teorema Bezout ditemukan, secara mengejutkan, oleh Etienne Bezout, seorang ahli matematika Prancis yang terutama berkaitan dengan aljabar. Teorema Bezout dapat dirumuskan sebagai berikut:

Mari kita cari tahu. P (x) adalah setiap polinomial dalam x, (x - a) adalah binomial di mana a adalah salah satu dari seluruh akar persamaan yang kita temukan di antara pembagi istilah bebas.
Tiga poin, ini adalah operator yang menunjukkan bahwa satu ekspresi dibagi oleh yang lain. Ini mengikuti dari ini yang telah menemukan setidaknya satu akar dari persamaan yang diberikan, kita dapat menerapkan teorema ini padanya. Tetapi mengapa teorema ini dibutuhkan, apa efeknya? Teorema Bezout adalah alat universal jika Anda ingin menurunkan derajat polinomial. Misalnya, dengan bantuannya, persamaan kubik dapat diubah menjadi persegi, biquadratic, kubik, dll.
Tapi itu satu hal untuk dipahami, tetapi bagaimana membagi? Tentu saja, Anda dapat membaginya dalam kolom, tetapi metode ini tidak tersedia untuk semua orang, dan kemungkinan membuat kesalahan sangat tinggi. Oleh karena itu, ada cara lain, ini adalah skema Horner. Saya akan menjelaskan pekerjaannya dengan sebuah contoh. Misalkan:

Jadi, kita telah diberi polinomial, dan kita mungkin telah menemukan salah satu akarnya di muka. Sekarang kita menggambar sepiring kecil 6 kolom dan 2 baris, di setiap kolom dari baris pertama (kecuali yang pertama), kami memperkenalkan koefisien dari persamaan. Dan di kolom pertama baris 2 kita menambahkan nilai a (root yang ditemukan). Kemudian koefisien pertama, dalam kasus kami 5, kami baru saja meledak. Nilai kolom berikut dihitung sebagai berikut:

(Gambar dipinjam di
sini )
Selanjutnya, kita melakukan hal yang sama dengan kolom lainnya. Nilai kolom terakhir (2 baris) akan menjadi sisa dari divisi, dalam kasus kami 0, jika Anda mendapatkan nomor selain 0, maka Anda harus memilih pendekatan yang berbeda. Contoh untuk persamaan kubik:

Persamaan Biquadratic yang Dapat Dikembalikan
Kami juga mempertimbangkan mengembalikan persamaan kubik di atas, dan sekarang kami menganalisis persamaan biquadratic. Pandangan umum mereka:

Tidak seperti persamaan pengembalian kubik, tidak semua orang memiliki pasangan biquadratic sehubungan dengan koefisien, tetapi sebaliknya mereka sangat mirip. Berikut adalah algoritma untuk menyelesaikan persamaan tersebut:

Seperti yang Anda lihat, menyelesaikan persamaan seperti itu sama sekali tidak sederhana. Tapi saya akan mengerti kasus ini. Solusinya dimulai dengan membagi seluruh persamaan dengan x ^ 2. Selanjutnya, kami kelompokkan, di sini saya secara khusus memperkenalkan garis tambahan untuk kejelasan. Setelah itu, kita melakukan trik, dan memasukkan braket pertama 2, yang pertama kita tambahkan, dan kemudian kurangi, jumlahnya tidak akan berubah, tapi sekarang kita bisa melipat braket ini ke dalam kuadrat jumlah.
Kami menghapus -2 dari braket, pertama kali mengalikannya dengan a, setelah itu kami memperkenalkan variabel baru, t dan mendapatkan persamaan kuadratik.
Sekarang mari kita beralih ke contoh:

Bagian utama, seperti dalam algoritma umum, dibagi dengan x ^ 2, dikelompokkan, diciutkan menjadi kotak penuh, kami melakukan substitusi variabel dan menyelesaikan persamaan kuadratik. Setelah itu, kami mengganti akar yang diperoleh kembali, dan menyelesaikan 2 persamaan kuadrat lainnya (dikalikan dengan x).
Bidang aplikasi
Karena kekakuan dan kekhususan mereka, persamaan derajat yang lebih tinggi jarang menemukan aplikasi mereka. Namun, masih ada contoh, persamaan Poisson untuk proses adiabatik dalam Fisika.
Kesimpulan
Dalam artikel ini, saya hanya mempertimbangkan persamaan kubik dan biquadratic. Namun, teorema Bezout yang dipertimbangkan (dan skema Horner) dapat digunakan untuk menyelesaikan persamaan 5, 6, 7 dan derajat lainnya, meskipun aplikasi mereka terbatas.